Для чего нужна погрешность

Погрешность

Чтобы качественно проводить маркетинговые исследования, необходимо учитывать погрешность измерений. Из-за пренебрежения этим параметром рекламная кампания может не пройти успешно и принести убытки фирме. Производя математические расчеты, удается получить данные, максимально приближенные к реальным цифрам.

Определение

Проводя измерение параметров рынка, маркетолог получает результаты в виде таблиц, графиков и пр. Эти данные он предоставляет заказчику. Но в отчетах не все специалисты указывают важную величину — погрешность, о которой клиент не подозревает.

Погрешность — это отклонение результата данных от измеряемой величины. Термин используется в физике, экономике и маркетинге.

Погрешность измерений — это сумма всех погрешностей, у каждой из которых имеется причина.

Оценка специалиста считается неточной, если эта величина не указана.

Что влияет на погрешность

На погрешность влияют:

неточности из-за принципа регистрации;

причины, объясняемые концевой мерой;

факторы, обусловленные исполнителем действий;

причины, провоцируемые изменениями условий.

Погрешность, связанная с методиками измерения (их несовершенство, упрощение) возникает из-за выбора примерных формул или неподходящего способа. Использование не того метода случается из-за несоответствия рассматриваемой величины и модели.

Факторы, влияющие на процесс:

Вариативность показаний — это самая явная разность показателей, полученных в прямом или обратном ходе при одинаковом действительном значении рассматриваемой величины и неизменных окружающих условий процесса.

Прецизионность — позволяет понять, насколько точно производятся расчеты. Определяется тем, насколько схожие получается показатели при одинаковых условиях измерений.

Классификация

Погрешности классифицируются по нескольким характеристикам. В маркетинговых исследованиях используются не все ее виды, поскольку погрешность в этой сфере не измеряется при помощи специальных приборов.

По форме представления

Первый тип — абсолютная погрешность. Она представляет собой алгебраическую разность между реальным и номинальными значениями. Она регистрируется в тех же величинах, что и основной объект. В расчетах абсолютный показатель помечается буквой ∆.

Например, линейка — наиболее простой и привычный каждому измерительный инструмент. При помощи верхней шкалы на ней определяются значения с точностью до миллиметра. Нижняя имеет другой масштаб (до 0,1 дюйма–2,54 мм). Несложно проверить, что на этом приборе погрешность верхней части меньше, чем нижней. Точность измерений в случае с линейкой будет зависеть от ее конструктивных особенностей.

Абсолютная погрешность измеряется той же единицей измерений, что и изучаемая величина. В процессе используется формула:

Δ = х1 – х2, где х1 — измеренная величина, а х2 — реальная величина.

Второй тип – относительная погрешность (проявляется в виде отношение абсолютного и истинного значения). Показатель не имеет собственной единица измерения или отражается процентно. В расчетах помечается как δ.

Она является более сложным значением, чем может показаться. В расчетах используется формула:

Стоит отметить, что если истинное значение имеет малую величину, то относительная — большую. Например, если стандартной линейкой (30 см) измеряется коробки (150 мм), то вычисление будет иметь вид: δ = 1 мм/150 мм = 0,66%. Если этот же прибор использовать для экрана смартфона (80 мм), то получится δ = 1 мм/80 мм = 1,25%. Получается, что в обоих случаях абсолютная погрешность не изменяется, но относительная отличается в разы. Во втором случае рекомендуется использовать более точный прибор.

Последний тип — приведенная погрешность. Она используется, чтобы не допустить такого разброса на одном приборе. Работает, как относительная, но вместо истинного значения в формуле применяется нормирующая шкала (общая длина линейки, например).

γ = (Δ / х3)·100 %, где х3 — это нормирующая шкала

Например, если потребуется измерить ту же коробку и смартфон, то придется учесть абсолютную величину в 1мм и приведенную погрешность — 1/300*100 =0,33 %. Если взять швейный метр и сравнить его с линейкой, то получится, что первый показатель в обоих случаях остается 1 мм, а второй отличается в разы (0,33% и 0,1%).

По причине возникновения

Тут выделяются два типа погрешностей:

Инструментальные — они объясняются особенностями строения измерительных приборов. Могут встречаться на фоне недостаточного качества частей оборудования. К такого рода погрешностям относят производство конструкции, ошибки из-за трения механизмов, малой жесткости поверхностей. Показатель отличается для любого из измерений и не может быть обобщен.

Методическая — это неточности расчетов, проявляющиеся из-за несовершенства применяемых методом, ошибок вычислений, соотношений, применяемых для оценки.

В маркетинге возможен только второй тип погрешности.

По характеру проявления

Выделяются систематические погрешности, которые характеризуются постоянными или закономерными изменениями показателей при повторных измерениях в пределах одной величины.

Другой вид — случайные погрешности. Они проявляются в произвольном порядке при повторном измерении одних и тех же величин.

Статическая погрешность — это неточность результата, характерная для статических измерений.

Динамическая погрешность — характерна для изменяемых величин.

По способу измерения

Выделяется погрешность градуировки приборов. Относится к действительному значению величины, указанному в той или другой отметке прибора в результате нанесения градуировки.

Также встречается неточность адекватности модели. Проявляется в виде неточности при подборе функциональной зависимости. В качестве примера можно взять процесс расчета линейной зависимости по сведениям, которые эффективнее отражаются совсем другим методом. Эта неточность используется для проверки модели.

Заключение

В маркетинге обычно используют данные статистической погрешности. Они помогают специалистам предварительно узнать результат и определить успешность рекламной кампании. Знание формул и умение проводить расчеты повышает экспертность и ценность специалиста.

Источник

Погрешность измерений

Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.

Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.

По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные

Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.

(1.2), где X — результат измерения; Х₀ — истинное значение этой величины.

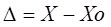
Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением

(1.3), где Х_д — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.

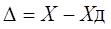
Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:

(1.4)

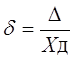
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные .

Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.

Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.

Систематические и прогрессирующие погрешности средств измерений вызываются:

Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.

Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.

По происхождению различают инструментальные и методические погрешности средств измерений.

Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.

Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.

Погрешности средств измерений.

Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:

(1.5), где X_н – номинальное значение меры; Х_д – действительное значение меры

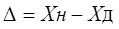
Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:

(1.6), где X_п – показания прибора; Х_д – действительное значение измеряемой величины.

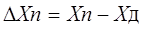
Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному

(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).

(1.7)

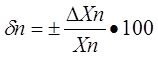
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).

(1.8)

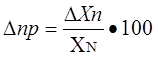
Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.

Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.

Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.

Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.

Факторы влияющие на погрешность измерений.

Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений

Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.

Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.

Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.

Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.

Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.

Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.

Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.

Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.

Шумы — любой сигнал не несущий полезной информации.

Источник

И снова о погрешностях

В современной школьной практике ученик на уроках физики сталкивается в основном c двумя типами эксперимента. Эксперимент первого типа – демонстрационный, его цель – демонстрация того или иного физического явления, установление качественной связи между физическими величинами, характеризующими явления или объекты. Если такой экс-перимент и предполагает измерение значений каких-либо величин, то точность этих измерений невелика. Главное – это доступность для понимания, наглядность, возможность достаточно быстро сделать выводы (например, демонстрация второго закона Ньютона: вдвое увеличили силу – ускорение изменилось приблизительно в два раза).

Школьные эксперименты второго типа – лабораторные работы в рамках программы. Здесь ученик сталкивается с необходимостью не только наблюдать и делать выводы, но и правильно обрабатывать результаты, определять значение величины и указывать её погрешность. Другие случаи, как правило, представляют собой комбинацию двух рассмотренных (практикум, самостоятельное исследование на уроке, фронтальный эксперимент).

Ни те, ни другие эксперименты не дают представления о роли физического эксперимента в развитии физики, однако государственный Стандарт по физике требует понимания учениками этой роли. Конечно, знакомясь с законами, полученными эмпирическим путем, учащийся не раз слышит фразу типа: «Георг Ом установил этот закон на основе многочисленных экспериментов». Но, как конкретно он это сделал, ученик вряд ли сможет объяснить. Остаётся неясным и смысл вычисления погрешностей при выполнении лабораторной работы.

Нельзя ли преподавать курс физики в соответствии с логикой самой науки? Проводить пусть немногочисленные, но настоящие эксперименты по определению вида зависимости пути от времени движения, угла преломления от угла падения, изменения температуры тела при теплообмене от его массы и т.д.? Такой подход связан с трудностями обучения школьников обработке результатов эксперимента. Ведь невозможно по экспериментальным данным получить вывод о конкретном виде зависимости между величинами, не поставив на графике «кресты» погрешностей. Значит, о погрешности следует говорить с самых первых шагов в физике. Но эта тема пугает даже некоторых опытных учителей.

Желая продемонстрировать своим ученикам роль эксперимента в физике, я на первых же уроках столк-нулась с тем, что очень трудно объяснить, кто и зачем выдумал такую вещь, как погрешность эксперимента. Причину этого я вижу в следующих ставшими уже традиционными моментах: 1) понятие погрешности вводится в 9-м классе, когда позади уже два года экспериментов и демонстраций без всякого рассмотрения точности полученного результата; 2) в наших учебниках в угоду простоте объяснения часто переиначивается сама цель введения погрешности; 3) в некоторых лабораторных работах вычисленные относительные погрешности превышают 100%, что ставит под сомнение саму цель вычисления погрешностей.

В связи с этим я попыталась перестроить всю систему обучения экспериментальному методу познания и оценке погрешностей результатов эксперимента. Большую помощь оказало знакомство со школой Светланы Вениаминовны Анофриковой, где уже разработана бульшая часть практической программы обучения экспериментальному методу познания в рамках технологии деятельностного подхода. В своей книге С.В.Анофрикова пишет: «При информационном обучении подобные ситуации (необходимость использования понятия погрешности. – Д.И.) в принципе не могут возникнуть. Поэтому всевозможные попытки обучить школьников методам обработки экспериментальных данных всегда оканчивались неудачей: в курс физики вводился новый и достаточно сложный материал, который, если и запоминался, то только формально, под давлением преподавателя, и не превращался в стиль мышления при проведении экспериментов даже у тех учащихся, которые планировали связать свою дальнейшую жизнь с физической наукой» [1].

Выход из сложившейся ситуации я вижу такой:

– переходить по мере возможности к преподаванию физики через совместное (учителя и учеников) «открытие» экспериментальных законов;

– вводить понятие погрешности измерений одновременно с понятием самого измерения (как, например, в [2]), используя творческую работу учащихся: самостоятельное изготовление измерительных приборов, проведение измерений в быту и т.д.;

– при использовании констант, табличных значений физических величин проводить вычисления с ними, как с приближёнными числами, используя понятия «значащая цифра», «погрешность округления». Это формирует определённый стиль мышления, учитывающий приближённость измеренных в эксперименте величин. Такое критическое отношение к результатам измерения имеет практическую важность для будущей «взрослой» жизни ученика, в какой бы области науки или отрасли производства он ни работал в дальнейшем;

– не оценивать строго правильность вычисления погрешностей, использования формул. Главное здесь всё же – понимание смысла и роли погрешности в эксперименте.

Тем не менее здесь я хочу предложить подробное изложение правильного подхода к обучению вычислению погрешности в школьном физическом эксперименте. В рассмотрение включены также конкретные вопросы, встречающиеся в практике работы с классическими и новыми учебниками. Важно, чтобы учитель мог самостоятельно разобраться с ними до того, как проблемы возникнут у учеников.

С технологией деятельностного подхода к обучению физике (авторская методика С.В.Анофриковой) можно познакомиться, например, в [1, 3, 4]. Большое количество сценариев таких уроков можно найти в газете «Физика» (ИД «Первое сентября»).

1. Зачем нужны погрешности?

Традиционно в школе рассчитывается «максимальная абсолютная погрешность» или «граница абсолютной погрешности». По сути, это ответ на вопрос: «На сколько максимально мы можем ошибиться в определении значения искомой величины?» При этом, если мы имеем несколько источников погрешностей в одном измерении, систематических и (или) случайных, погрешность результата измерения определяется как сумма всех погрешностей и называется максимальной. Хотя такое суммирование неправомерно (складываться должны не погрешности, а их квадраты) [квадраты погрешностей складываются для не зависящих друг от друга величин, а сами погрешности – для зависящих. – Ред.], тем не менее даже такой упрощённый подход даёт возможность показать смысл введения понятия погрешности.

Так зачем же нужны погрешности? Известно, что любые измерения, т.е. любое измеренное или рассчитанное значение физической величины, не могут быть абсолютно точными. Как тогда решать вопрос, например, о равенстве двух значений? Как провести кривую на графике? Приведу пример.

В учебнике А.В.Пёрышкина «Физика-8» [5], а также в учебнике С.В.Громова, Н.А.Родиной «Физика-8» [6] есть лабораторная работа «Сравнение количеств теплоты при смешивании воды разной температуры». Её результатом должно стать сравнение двух значений количества теплоты. Но какой вывод, не зная ничего о существовании погрешности эксперимента, должны сделать учащиеся? Ведь полученные значения заведомо не могут быть равны! Проблемы с выводом возникают и в работе «Измерение силы трения скольжения» [6]; там предлагается выяснить, зависит ли коэффициент трения от веса тела.

Можно предложить такой выход. Если учащиеся уже знают, что при измерениях результаты всегда не очень точные, то в работе о сравнении количеств теплоты можно предложить округлить полученные результаты, предварительно выразив количества теплоты в килоджоулях. Но есть вероятность, что и после этого значения окажутся различными. А вычислить абсолютную погрешность (далее я для простоты опускаю слово «максимальную») «методом границ» (о нём – дальше) не так уж сложно. Зато эффект от самостоятельно проведённого опыта возрастает многократно!

Итак, абсолютной погрешностью измерения называют модуль разности между истинным значением величины и её значением, полученным в результате измерения:

Важно здесь то, что истинное значение величины узнать нельзя! Зато с помощью серии измерений и обработки их результатов можно найти её приблизительное значение и оценить возможное отклонение от него измеренной величины. К сожалению, этот смысл погрешности часто ускользает от наших учеников нашими же стараниями. Приведу пример.

Чтобы понимать, насколько велика погрешность по сравнению с самой величиной, вводят понятие относительной погрешности измерения:

Так как истинного значения мы не знаем, то при не очень больших значениях относительной погрешности можно заменить в этой формуле а_{истинное} измеренным значением а. Величина относительной погрешности играет важную роль в определении «качества» поставленного эксперимента. Если она составляет 30–40%, то в школьном эксперименте это ещё допустимо (особенно, если учесть, что мы работаем с максимальной абсолютной погрешностью). А вот измерений, при которых относительная погрешность заведомо больше этих значений, надо попросту избегать.

2. Типы погрешностей

Погрешности измерений принято подразделять на систематические и случайные [9, 10].

Систематические погрешности вызываются факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений. Величину систематической погрешности можно пытаться уменьшить, улучшая условия проведения эксперимента, выбирая более точные приборы и т.д.

Случайные погрешности – те, значения которых могут отличаться от измерения к измерению на неизвестную нам, случайную величину. Если провести ряд измерений и взять среднее арифметическое из этого ряда, то случайная погрешность этого среднего будет меньше, чем погрешность единичного измерения. Так стараются уменьшить величину случайной погрешности эксперимента.

Наконец, грубые промахи – погрешности вследствие неправильных действий при измерении. Чтобы исключить их, надо соблюдать аккуратность и тщательность в работе и записях результатов. При необходимости такие измерения надо произвести повторно. В дальнейшем мы не будем говорить об этом типе погрешностей эксперимента.

Прежде чем перейти к более подробному, с примерами, рассмотрению различных видов погрешностей, разберёмся, как они должны сочетаться в конечном результате. При расчёте среднеквадратичных погрешностей складываются не сами погрешности, а их квадраты [9]. Ясно, что введение в ученический эксперимент такого правила сильно усложнило бы и без того не очень простой процесс. При расчёте максимальной абсолютной погрешности можно складывать погрешности, имеющие различную природу, но соблюдая «правило ничтожных погрешностей» [2, 8]: При суммировании погрешностей любым слагаемым можно пренебречь, если оно не превосходит 25–30% от другого.

Действительно, если одно из значений меньше другого в 3 раза, то после возведения в квадрат оно составит всего лишь около 10% от другого слагаемого. Это правило помогает избегать ситуаций, когда при накоплении «малых» погрешностей, погрешность результата сильно возрастает. Ниже я приведу пример расчёта среднеквадратичной погрешности и максимальной погрешности измерений. И наконец, последнее правило:

если систематическая погрешность является определяющей, т.е. её величина существенно больше величины случайной погрешности, то достаточно выполнить измерение один раз; если определяющей является случайная погрешность, то измерение следует проводить несколько раз.

3. Учёт систематической погрешности при прямых измерениях

Существует много видов систематических погрешностей. В практике школьного эксперимента встречаются только приборные (инструментальные) погрешности, погрешность округления (отсчёта) и субъективные погрешности (например, точность измерений секундомером ограничена временем реакции, равным примерно 0,3 с). Рассмотрим данные виды погрешностей подробней.

Инструментальная погрешность _иА – это систематическая погрешность измерения, определяемая свойствами измерительного прибора. Её значение указано в паспорте прибора. Обычно это класс точности прибора, показывающий, сколько процентов от максимального показания шкалы прибора составляет значение абсолютной погрешности измерения. На мой взгляд, лучше иметь таблицу абсолютных инструментальных погрешностей для приборов, используемых в лабораторных работах (см., например, [11].

Особо следует сказать об инструментальной погрешности весов и разновесов. Её вычисление сложно для семиклассников (да и для десятиклассников), и я считаю такие вычисления излишними за исключением физико-математических классов. Здесь спасает следующее соображение. Точность измерения массы с помощью весов очень велика – относительная погрешность менее 1%, тогда как относительная погрешность измерения, например, объёма в лабораторной работе по определению плотности тела обычно не меньше 5%. Поэтому проще учитывать погрешность измерения массы с помощью весов через интервал округления (систематическая погрешность отсчёта).

Погрешность отсчёта ₀А – это систематическая погрешность, появляющаяся в результате округления измеряемого значения в процессе снятия показаний. Обычно в школьном эксперименте погрешность отсчёта принимают равной половине цены деления прибора [2, 8]. Иногда это приводит к необоснованному, на мой взгляд, завышению значения погрешности. Приведу ряд примеров:

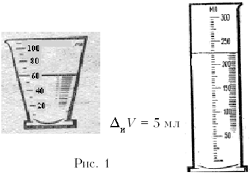
На рис. 1 приведены шкалы двух мензурок и значения инструментальной погрешности для них. Уровень жидкости в обеих мензурках совпадает с одним из штрихов шкалы. Если воспользоваться приведённым способом оценки погрешности отсчёта, то погрешность определения объёма левой мензуркой
V_лев = _иV + ₀V = 5 мл + 5 мл = 10 мл, а правой
V_прав = 5 мл + 2,5 мл = 7,5 мл. Но совпадение уровня жидкости со штрихом шкалы фиксируется с достаточной точностью! Зачем же завышать погрешность измерения в 2 раза в первом случае и в 1,5 раза во втором? [Тонкий вопрос: а параллакс при считывании показаний? а явление смачивания? – Ред.] Другое дело, если уровень жидкости не совпадает с делением шкалы. Но тогда возможен вариант «уровень выше штриха примерно на четверть (половину, три четверти) деления».

Удобнее в таком случае ввести понятие «интервал округления». Если мы округляем показания прибора до целого деления, то интервал округления равен цене деления прибора, если отсчёт округляется до половины деления («на глаз»), то интервал округления равен половине цены деления, и т.д. При округлении погрешность не превышает половины интервала округления [1]. Такой подход позволяет свести все случаи к оценке интервала округления.

Пусть в левой мензурке уровень жидкости ближе к середине деления, чем к штриху 60 мл, и мы можем сказать, что объём равен примерно 65 мл. Тогда интервал округления составляет половину цены деления, т.е. 5 мл, а погрешность отсчёта 2,5 мл. Итак, окончательное значение объёма (65,0 ± 7,5) мл (о количестве значащих цифр в значении погрешности – позже).

В случае совпадения (или приблизительного совпадения) уровня жидкости со штрихом шкалы можно считать, что интервал округления очень мал (например, 2 мл), так что погрешностью отсчёта можно пренебречь по сравнению с инструментальной погрешностью мензурки.

При измерении объёма правой мензуркой деления настолько малы, что надёжно можно фиксировать лишь близость уровня жидкости к одному или другому штриху шкалы. Тогда интервал округления будет равен цене деления шкалы, а погрешность – половине цены деления, т.е. 2,5 мл.

Иногда погрешность отсчёта становится больше инструментальной погрешности в силу условий эксперимента. Например, в лабораторном наборе «Механика» лаборатории L-micro есть магнитные датчики, включающие и выключающие секундомер при прохождении мимо них тела. Положение датчиков определяется по линейке, но отверстия датчиков имеют размер около 2 мм, так что положение самого датчика невозможно определить точнее, чем 1 мм. С учётом инструментальной погрешности линейки абсолютная погрешность определения координаты датчика составляет 2 мм.

В лабораторной работе «Определение КПД при подъёме тела по наклонной плоскости» [12] значение высоты и длины наклонной плоскости определяется с помощью ученической линейки. Хотя цена деления её 1 мм, погрешность отсчёта больше 0,5 мм. Дело в том, что для правильного определения высоты необходимо держать линейку строго вертикально и измерять расстояние до верхней грани плоскости. Это измерение трудно проделать с точностью меньше 1 мм.

Ещё сложнее измерить высоту, с которой скатывается цилиндр по наклонной плоскости, в работе «Измерение момента инерции тела» [2] или при измерении ускорения тела, скатывающегося с наклонной плоскости [7]. Ведь необходимо измерять высоту и длину плоскости между определёнными точками, в которых находилось тело в начальный и конечный моменты времени. Поскольку нет смысла вводить ещё одно понятие – «систематическая погрешность, определяемая условиями эксперимента», – следует обратить внимание учащихся на неточность измерений и после обсуждения с ними увеличить погрешность отсчёта.

Очень полезно понятие интервала округления при определении погрешности табличных значений или значений констант. Например:

При измерении времени секундомером большую роль играет субъективная погрешность. Время реакции человека составляет 0,1–0,2 с [10]. Поэтому систематическая погрешность – около 0,3–0,4 с (реакция при запуске и реакция при остановке).

И в заключение – об округлении значения абсолютной погрешности. Обычно его округляют до одной значащей цифры (т.е. первой не равной нулю цифры слева). Исключение составляют случаи, когда единственная оставшаяся значащая цифра в значении погрешности – единица. В таких случаях лучше оставить две значащие цифры, т.к. погрешность такого округления очень велика. (Если мы округлим, например, 0,14 до 0,1, то относительная погрешность округления составит 40%, так что лучше оставить 0,14).

В значении самой величины оставляют столько же десятичных знаков, сколько их в значении погрешности (см. записи в приведённых примерах).

Так следует поступать, если полученный результат является конечным. Если же он промежуточный, то, по правилам приближённых вычислений, следует оставлять на одну значащую цифру больше.

Продолжение в № 17/07

* В [6] в этом месте в ЛР № 2 допущена опечатка.

Источник