Доказать что через три данные точки лежащие на прямой проходит плоскость

Через три точки можно провести плоскость

Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Существование плоскости, проходящей через три данные точки

Существование плоскости, проходящей через три данные точки

Теорема 15.3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

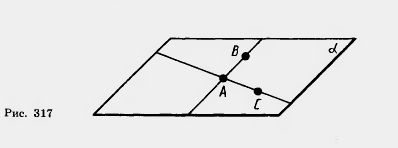
Доказательство. Пусть А, В, С — три данные точки, не лежащие на одной прямой (рис. 317). Проведем прямые АВ и АС; они различны, так как точки А, В, С не лежат на одной прямой. По аксиоме Сз через прямые АВ и АС можно провести плоскость . Эта плоскость содержит точки А, В, С.

Докажем, что плоскость а, проходящая через точки А, В, С, единственна. Действительно, плоскость, проходящая через точки А, В, С, по теореме 15.2 содержит прямые АВ и АС. А по аксиоме Сз такая плоскость единственна.

Задача (13). Можно ли провести плоскость через три точки, если они лежат на одной прямой? Объясните ответ.

Решение. Пусть А, В, С — три точки, лежащие на прямой . Возьмем точку D, не лежащую на прямой (аксиома I). Через точки А, В, D можно провести плоскость (теорема 15.3). Эта плоскость содержит две точки прямой — точки A и В, а значит, содержит и точку С этой прямой (теорема 15.2).

Следовательно, через три точки, лежащие на одной прямой, всегда можно провести плоскость.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.

сколько плоскостей можно провести через

две различные точки

три различные точки

четыре точки никакие три из которых не лежат на одной прямой.

В рамках этого материала мы разберем, как найти уравнение плоскости, если мы знаем координаты трех различных ее точек, которые не лежат на одной прямой. Для этого нам понадобится вспомнить, что такое прямоугольная система координат в трехмерном пространстве. Для начала мы введем основной принцип данного уравнения и покажем, как именно использовать его при решении конкретных задач.

Как найти уравнение плоскости, которая проходит через 3 заданные точки

Для начала нам необходимо вспомнить одну аксиому, которая звучит следующим образом:

Если три точки не совпадают друг с другом и не лежат на одной прямой, то в трехмерном пространстве через них проходит только одна плоскость.

Иными словами, если у нас есть три разных точки, координаты которых не совпадают и которые нельзя соединить прямой, то мы можем определить плоскость, проходящую через нее.

Зная координаты нормального вектора и координаты точки, через которую проходит плоскость, мы можем записать общее уравнение этой плоскости.

Из этого мы и будем исходить в дальнейшем.

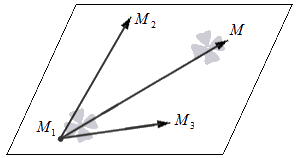
n → = M 1 M 2 → × M 1 M 3 → = i → j → k → x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1

На схеме это будет выглядеть так:

Запишем полученное уравнение в координатной форме:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0

От полученного в результате уравнения можно перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости, если этого требуют условия задачи.

В следующем пункте мы приведем примеры того, как указанные нами подходы реализуются на практике.

Примеры задач на составление уравнения плоскости, проходящих через 3 точки

Ранее мы выделили два подхода, с помощью которых можно найти искомое уравнение. Давайте посмотрим, как они применяются в решениях задач и когда следует выбирать каждый из них.

Решение

Используем поочередно оба способа.

Теперь вычислим их векторное произведение. Вычисления определителя расписывать при этом не будем:

n → = M 1 M 2 → × M 1 M 3 → = i → j → k → 2 0 5 6 1 0 = – 5 · i → + 30 · j → + 2 · k →

Это и есть нужное нам уравнение плоскости, которая проходит через три точки.

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = x – ( – 3 ) y – 2 z – ( – 1 ) – 1 – ( – 3 ) 2 – 2 4 – ( – 1 ) 3 – ( – 3 ) 3 – 2 – 1 – ( – 1 ) = = x + 3 y – 2 z + 1 2 0 5 6 1 0 = – 5 x + 30 y + 2 z – 73

Мы получили нужное нам уравнение.

А как быть, если заданные точки все же лежат на одной прямой и нам нужно составить уравнение плоскости для них? Здесь сразу надо сказать, что это условие будет не совсем корректным. Через такие точки может проходить бесконечно много плоскостей, поэтому вычислить один-единственный ответ невозможно. Рассмотрим такую задачу, чтобы доказать некорректность подобной постановки вопроса.

Решение

Векторное произведение будет равно:

M 1 M 2 → × M 1 M 3 → = i → j → k → – 4 6 2 – 6 9 3 = 0 · i ⇀ + 0 · j → + 0 · k → = 0 →

Если мы используем второй способ, у нас получится:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0 ⇔ x – 5 y – ( – 8 ) z – ( – 2 ) 1 – 5 – 2 – ( – 8 ) 0 – ( – 2 ) – 1 – 5 1 – ( – 8 ) 1 – ( – 2 ) = 0 ⇔ ⇔ x – 5 y + 8 z + 2 – 4 6 2 – 6 9 3 = 0 ⇔ 0 ≡ 0

Если вы хотите найти хоть один ответ этой задачи из бесконечного множества ее вариантов, то нужно выполнить следующие шаги:

Источник

Лекция по математике на тему «Аксиомы стереометрии»

Аксиома – это утверждение не требующее доказательства.

Аксиомы стереометрии – утверждения о свойствах геометрических тел, принимаемые в качестве исходных положений, на основе которых доказываются все теоремы и вообще строится вся геометрия.

Аксиома А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Аксиома А1 состоит из двух частей.

Первая часть утверждает, что через три точки проходит плоскость, т.е. существует хотя бы одна плоскость.

А вторая часть аксиомы говорит, что такая плоскость только одна.

Символ читается как существует.

По этой аксиоме, три точки, не лежащие на одной прямой, однозначно определяют плоскость.

Поэтому плоскости иногда обозначают тремя большими буквами, используя любые три точки плоскости, не лежащие на одной прямой.

У нас на экране плоскость обозначена как α. Эту же плоскость можно обозначить как ABC

Аксиома 1 (существование плоскости)

Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

, причем α – единственная.

Аксиома А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

В этом случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую.

Эта аксиома устанавливает взаимосвязь между прямой и плоскостью, то есть тот факт, что плоскость действительно плоская и прямая ее не «протыкает», а целиком содержится в ней.

Из аксиомы A 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки.

Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.

Если две точки прямой лежат в плоскости, то все точки этой прямой лежат в этой плоскости.

В этом случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую.

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

В этом случае говорят, что плоскости пересекаются по прямой, проходящей через эту точку..

Эта аксиома очень важная. Она утверждает, что две плоскости не могут пересекаться по одной единственной точке.

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Говорят, что плоскости пересекаются по прямой, проходящей через эту точку.

Справедливость фактов планиметрии

Мы с вами познакомились с тремя аксиомами стереометрии.

Возникает вопрос: «Можем ли мы пользоваться теми фактами, которые справедливы на плоскости: теорема Пифагора, формулы площади треугольников, параллелограмма? Или все эти формулы, теоремы для нас уже не имеют значения?»

В планиметрии мы имели дело с одной плоскостью, на которой располагались все рассматриваемые нами фигуры. В стереометрии много плоскостей.

И в каждой из плоскостей, справедливы все факты планиметрии. В любой из плоскостей выполняется теорема Пифагора для прямоугольного треугольника, верны формулы длины окружности, верны формулы для площади.

Все что мы изучали, мы теперь можем применять смело в каждой из рассматриваемых плоскостей.

Аксиомы стереометрии не противоречат аксиомам планиметрии.

В стереометрии принимаются все факты планиметрии для каждой плоскости.

Переходим к решению задач

Задача 1. По рисунку назовите:

По рисунку назовите:

Аналогично:

Аналогично: .

Аналогично:

Могут ли какие-то три из них лежать на одной прямой?

Найти: Могут ли 3 из них лежать на одной прямой?

Две точки A и С прямой m принадлежат в плоскости , значит и точка B этой прямой принадлежит этой плоскости.

Получается, что в одной плоскости лежат все четыре точки, что противоречит условию задачи. Значит предположение неверно, никакие три точки не лежат на одной прямой.

лежать на одной прямой.

Могут ли какие-то три из них лежать на одной прямой?

Найти: Могут ли 3 из них лежать на одной прямой?

Пусть:

(аксиома А1)

(аксиома А2)

. Получили противоречие, по условию задачи точки не лежат в одной плоскости.

Предположение неверно, никакие три точки не лежат на одной прямой.

Задача 3. Докажите, что через три данные точки, лежащие на одной прямой, проходит плоскость. Сколько существует таких плоскостей?

Найти :Количество плоскостей

Так как две точки A и C прямой m принадлежат плоскости α, то и точка B прямой m принадлежит этой плоскости.

Все три точки принадлежат плоскости.

Значит плоскость α – искомая плоскость.

Ответ: Через три данные точки, лежащие на одной прямой, может проходить

бесконечное множество плоскостей.

Доказать:

Найти: Количество плоскостей

Пусть .

(аксиома A 1).

(аксиома A 2).

Плоскость α – искомая плоскость.

Т. к D – произвольная точка, то таких плоскостей бесконечное множество.

Ответ: бесконечное множество.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-025570

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

В России планируют создавать пространства для подростков

Время чтения: 2 минуты

В России будут создавать школьные театры

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Создана Ассоциация руководителей школ России и Беларуси

Время чтения: 1 минута

Минпросвещения сформирует новый федеральный перечень учебников

Время чтения: 2 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Стереометрия. Страница 1

1. Основные фигуры стереометрии

Аксиомы планиметрии описывают свойства простейших геометрических фигур на плоскости. Так как стереометрия изучает фигуры в пространстве и в пространстве может быть великое множество плоскостей, то аксиомы стереометрии состоят из аксиом планиметрии с уточнением «на» или «в заданной плоскости» и 3-х дополнительных аксиом.

2. Группа дополнительных аксиом стереометрии

1. Для любой плоскости в пространстве, существуют точки принадлежащие данной плоскости и точки не принадлежащие ей.

2. Две различные плоскости, имеющие одну общую точку, пересекаются по прямой, проходящей через эту точку.

3. Через две различные прямые, имеющие общую точку, можно провести только одну плоскость.

Рис. 1. Аксиомы стереометрии.

Пример

Даны три попарно пересекающиеся плоскости. Две прямые пересечения из них пересекаются. Доказать, что три прямые пересечения этих плоскостей пересекаются в одной точке.

Пусть даны три попарно пересекающиеся плоскости α, β и γ. Плоскость α пересекает плоскость β по прямой а. А плоскость β пересекает плоскость γ по прямой с (Рис. 2 а).

точка Е ∈ а,с (прямые пересекаются в точке Е по условию задачи)

Тогда плоскости α и γ пересекаются по прямой b.

Отсюда следует, что, т.к. прямые b,с ∈ γ, то они либо параллельны, либо пересекаются в какой-то точке Е₁.

Если они параллельны, то у них нет общих точек, а следовательно, плоскости α и β пересекаются по прямой а, параллельной b и с (Рис. 2 б). А это противоречит условию задачи. Следовательно, прямые b и с пересекаются в какой-то точке Е₁.

Отсюда можно сделать вывод, что точка Е₁ принадлежит трем плоскостям α,β,γ и, следовательно, она лежит одновременно на трех прямых а, b и с. А это возможно только, если три прямые пересекаются в одной точке. И, следовательно, прямая b пересекает прямую с в точке Е₁, которая является точкой пересечения прямых а и с. Таким образом, точки Е и Е₁ совпадают.

Рис.2. Даны три попарно пересекающиеся плоскости.

3. Плоскость, проходящая через данную прямую и точку

Теорема: Через прямую и не лежащую на ней точку можно провести только одну плоскость.

Доказательство.

Пусть АВ данная прямая и Е не принадлежащая ей точка. (Рис.3) Проведем через точки А и Е прямую. Тогда прямые АВ и АЕ пересекаются в точке А. Согласно аксиоме: через две пересекающиеся прямые можно провести только одну плоскость, плоскость α, проведенная через эти прямые, единственная. Т.к. точка Е принадлежит прямой АЕ, то она принадлежит плоскости α.

Если допустить, что существует еще одна плоскость α’, проходящая через прямую АВ и точку Е, то эта плоскость пересекает плоскость α по прямой, на которой лежат точки А, В, и Е согласно аксиоме 2. А это противоречит условию, т.к. точки А, В, и Е не лежат на одной прямой. Следовательно, плоскость α единственная.

Рис. 3 Плоскость, проходящая через данную прямую и точку.

4. Пересечение прямой с плоскостью

Теорема: Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит данной плоскости.

Доказательство.

Проведем через прямую а и точку С плоскость β. Тогда, если плоскости α и β совпадают, то прямая а принадлежит плоскости α, что и утверждает данная теорема. Если плоскости α и β не совпадают, то они пересекаются по прямой а’. Таким образом, имеем:

точки А и В ∈ а, α
прямая а ∈ β
следовательно, точки А и В ∈β

Отсюда следует, что две точки А и В принадлежат двум плоскостям: α и β. И, согласно аксиоме, они могут лежать только на прямой а’, которая является прямой пересечения этих плоскостей. Т.к. через две точки можно провести только одну прямую, и по условию теоремы эта прямая есть а, то следовательно, она и является прямой пересечения двух плоскостей. Т.е. прямые а и а’ совпадают. А следовательно, прямая а принадлежит плоскости α.

Из данной теоремы следует, что плоскость и не принадлежащая ей прямая, либо не пересекаются, либо пересекаются в одной точке.

Рис. 4 Пересечение прямой с плоскостью.

5. Существование плоскости, проходящей через три данные точки

Теорема. Через три точки, не лежащие на данной прямой, можно провести только одну плоскость. Рис.5

Доказательство. Пусть А, В, С три точки, не лежащие на одной прямой. Проведем через точки А,С и В,С прямые. Тогда они пересекаются в точке С. Согласно аксиоме: через две пересекающиеся прямые можно провести только одну плоскость, плоскость, проведенная через эти прямые, единственная. По теореме о пересечении прямой с плоскостью, обе прямые целиком принадлежат данной плоскости.

Рис. 5 Существование плоскости, проходящей через три данные точки.

6.Пример 1

Докажите, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.

Доказательство:

Пусть дана данная прямая а и точка О, не принадлежащая прямой а. И даны пересекающие ее прямые b, c, d в точках B, C, D, которые пересекаются в точке О. Проведем через прямую а и точку О плоскость α (Рис.6).

По теореме о пересечении прямой и плоскости, если провести прямую b, проходящую через точку О и точку В прямой а, то она целиком будет принадлежать плоскости α, так как две точки прямой b принадлежат плоскости α.

Если допустить, что прямая b не принадлежит плоскости α, то в этом случае мы можем провести плоскость α’, проходящую через точки В и О. Тогда плоскости α и α’ пересекаются по прямой b’, проходящей через точки В и О. А так как через две точки можно провести только одну прямую, то прямые b и b’ совпадают. Следовательно, прямая b целиком принадлежит плоскости α.

Точно так же доказывается, что прямые с и d принадлежат плоскости α. Отсюда можно сделать вывод, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.

Рис.6 Задача. Докажите, что все прямые, пересекающие данную прямую.

Пример 2

Даны две непересекающиеся плоскости. Докажите, что прямая, пересекающая одну из этих плоскостей, пересекает и другую.

Доказательство:

Пусть даны две непересекающиеся плоскости α и α’. И прямая а, которая пересекает плоскость α в точке В (Рис.7). Необходимо доказать, что прямая а пересекает плоскость α’ в точке В’.

Возьмем на плоскости α’ точку А и проведем через нее и прямую а плоскость β. Тогда плоскость β будет пересекать плоскости α и α’ по параллельным прямым b и b’. Точка В принадлежит прямой b, так как она принадлежит плоскости α и лежит на прямой а. И следовательно, она принадлежит двум плоскостям α и β.

Таким образом получается, что на плоскости β лежат две параллельные прямые b и b’. Одну из них пересекает прямая а в точке В. Следовательно, прямая а пересекает и вторую прямую b’. Так как согласно аксеоме, через точку В, не лежащей на данной прямой b’, можно провести только одну, параллельную прямой b’, прямую b. Отсюда следует, что прямая а не параллельна прямой b’, она ее пересекает в точке B’.

Рис.7 Задача. Даны две непересекающиеся плоскости.

Пример 3

Даны две плоскости, пересекающиеся по прямой а. И прямая b, которая лежит в одной из этих плоскостей и пересекает другую. Докажите, что прямые а и b пересекаются.

Доказательство:

Пусть даны две пересекающиеся плоскости α и β. Прямая а, является их прямой пересечения. Прямая b лежит в плоскости β и пересекает плоскость α в точке А (Рис.8). Необходимо доказать, что прямая b пересекает прямую а.

По условию задачи, прямая b лежит в плоскости β и пересекает плоскость α в точке А. Следовательно, точка А принадлежит двум плоскостям α и β.

Согласно аксиоме стереометрии, если две плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Отсюда следует, что, так как точка А принадлежит двум плоскостям, то она лежит на прямой а, потому что прямая а является прямой пересечения двух плоскостей α и β.

Таким образом, точка А принадлежит двум прямым а и b. А следовательно, эти прямые пересекаются.

Рис.8 Задача. Даны две плоскости, пересекающиеся по прямой а.

Пример 4

Точки А, В, С лежат в каждой из двух различных плоскостей. Докажите, что эти точки лежат на одной прямой.

Доказательство:

Пусть даны две пересекающиеся плоскости α и β. Прямая а, является их прямой пересечения. Точки А, В, С одновременно принадлежат двум плоскостям α и β (Рис.9). Необходимо доказать, что все три точки принадлежат прямой а.

Согласно аксиоме стереометрии, если две плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Отсюда следует, что все три точки А, В и С лежат на прямой пересечения двух плоскостей, т.е. прямой а, так как они принадлежат обоим плоскостям α и β.

Пусть дана точка D, принадлежащая только плоскости β. Тогда она не может лежать на прямой а, так как она не принадлежит плоскости α. Точно так же точка Е не может принадлежать прямой а, так как она принадлежит только плоскости α. Точка F не принадлежит плоскостям α и β, а следовательно, и прямой а.

Рис.9 Задача. Точки А, В, С лежат в каждой из двух различных плоскостей.

Пример 5

Даны четыре точки. Известно, что прямая, проходящая через любые две из этих точек, не пересекается с прямой, проходящей через другие две точки. Докажите, что данные четыре точки не лежат в одной плоскости.

Доказательство:

Пусть даны четыре точки А, В, С, D. Допустим, что все четыре точки лежат в одной плоскости α.

Прямая АВ не пересекается с прямой CD. Прямая АС также не пересекается с прямой BD. Если провести прямую AD, то точки В и С окажутся в разных полуплоскостях. Следовательно, прямая AD пересекается с прямой ВС в точке О (Рис.10 а).

Допустим, что прямая AB не пересекает прямую DС (Рис.10 б). АD не пересекает прямую BC. Тогда, если провести прямую АС, то точки B и D окажутся в разных полуплоскостях. И прямая АС будет пересекать прямую BD в точке О.

Теперь допустим, что прямая AC не пересекает прямую ВD (Рис.10 в). АD не пересекает прямую ВC. Тогда, если провести прямую АВ, то точки D и C окажутся в разны полуплоскостях. А следовательно, прямая АВ будет пересекать прямую СD в точке О.

Отсюда можно сделать вывод, для того, чтобы выполнялось условие, при котором прямые АВ, АС, АD, одновременно не пересекали бы прямые CD, BD, BC, необходимо чтобы четыре точки А, В, С и D лежали в разных плоскостях.

Рис.10 Задача. Даны четыре точки. Известно, что прямая.

Источник

• Популярная книга Круть доступна для чтения прямо сейчас на нашем сайте boochi.ru. Скачать книгу в формате FB2, TXT, PDF, EPUB бесплатно без регистрации. →

Главная > Учебные материалы > Математика: Стереометрия. Страница 1