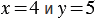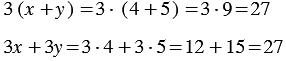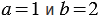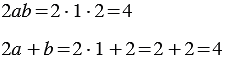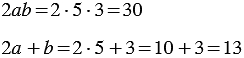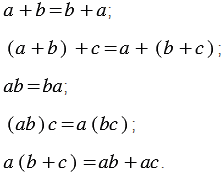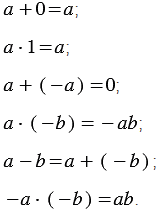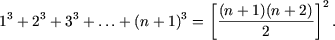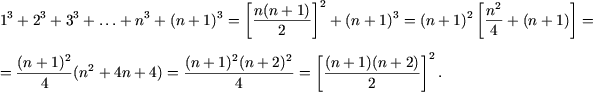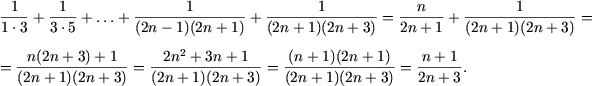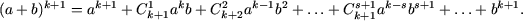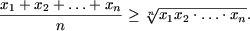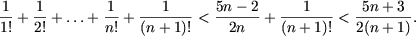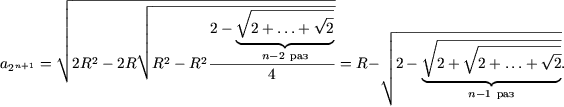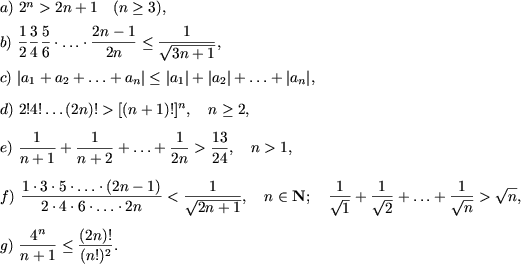Доказать что равенство верно
Числовые равенства, свойства числовых равенств
После получения общих сведений о равенствах в математике переходим к более узким темам. Материал этой статьи даст представление о свойствах числовых равенств.
Что такое числовое равенство
Числовое равенство – это равенство, обе части которого состоят из чисел и/или числовых выражений.
Свойства числовых равенств
Сложно переоценить значимость свойств числовых равенств в математике: они являются опорой многому, определяют принцип работы с числовыми равенствами, методы решений, правила работы с формулами и многое другое.Очевидно, что существует необходимость детального изучения свойств числовых равенств.
Свойства числовых равенств абсолютно согласованы с тем, как определяются действия с числами, а также с определением равных чисел через разность: число a равно числу b только в тех случаях, когда разность a − b есть нуль. Далее в описании каждого свойства мы проследим эту связь.
Основные свойства числовых равенств
Изучать свойства числовых равенств начнем с трех базовых свойств, которые присущи всем равенствам. Перечислим основные свойства числовых равенств:
Прочие важные свойства числовых равенств
Основные свойства числовых равенств, рассмотренные выше, являются базисом для ряда дополнительных свойств, довольно ценных в разрезе практики. Перечислим их:
Укажем еще на пару свойств, которые позволяют осуществлять сложение и умножение соответствующих частей верных числовых равенств:
Необходимо уточнить, что почленно можно сложить не только два верных числовых равенства, но и три, и более;
Завершим данную статью, собрав для наглядности все рассмотренные свойства:
Тождественно равные выражения. Тождества
| Два выражения, значения которых равны при любых значениях переменных, называют тождественно равными. |
Рассмотрим две пары выражений:
1) 
Найдем их значения при
Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных 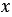
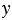

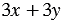
2)
Найдем их значения при
Мы получили один и тот же результат. Однако, можно указать такие значения 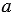
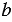
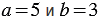
Мы получили разные результаты.
Следовательно, выражения 
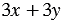
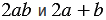
| Равенство, верное при любых значениях переменных, называется тождеством. |
Равенство 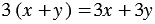
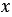
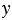
Также к тождествам можно отнести равенства, выражающие свойства сложения и умножения чисел:
Можно привести и другие примеры тождеств:
Тождествами считают и верные числовые равенства.
Очень часто при вычислении значений выражений, легче сначала упростить имеющееся выражение, а затем выполнять вычисления.
| Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения. |
К тождественным преобразованиям можно отнести приведение подобных слагаемых и раскрытие скобок.
Примеры:
1) 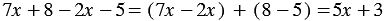
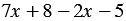
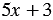
2) 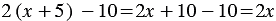
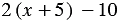
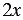
Для того, чтобы доказать, что данное равенство является тождеством (или доказать тождество), используют следующие методы:
1) тождественно преобразуют одну из частей данного равенства, получая другую часть;
2) тождественно преобразуют каждую из частей данного равенства, получая одно и то же выражение;
3) доказывают, что разность левой и правой частей данного равенства тождественно равна нулю.
Также, чтобы доказать, что равенство не является тождеством, достаточно привести контрпример, т.е. указать такое значение переменной (или переменных, если их несколько), при котором данное равенство не выполняется.
Пример: Докажите, что равенство 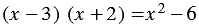
Решение: Приведем контрпример. Если 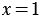
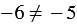
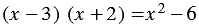
Поделись с друзьями в социальных сетях:
Доказать, что равенство верно
Всем привет, вот такая задачка мне попалась.
Вот как я ее доказал, прошу совета, правильно ли я ее доказал, можно ли так доказывать?
Доказательство:
Положим, что вектор «a» нулевой, «b» и «c» противоположные векторы, тогда сумма нуль-вектора и двух противоположных векторов нам даст 0. Первая часть задачи доказана. Вторая часть. Выполняем векторное произведение в первых квадратных скобках: нуль-вектор на вектор, дает нам нуль-вектор. Далее выполняем векторное произведение во вторых квадратных скобках: векторное произведение двух противоположных векторов дает нам нуль-вектор. Выполняем произведение в третьих квадратных скобках: нуль-вектор на вектор, дает нам нуль-вектор, в итоге у нас получается равенство трех квадратных скобок, что соответствует условию задачи.
Доказано.
Можно с таким к преподавателю подходить?
Добавлено через 3 минуты
Ой, пардон за название темы, поправьте пожалуйста.

x³+y³+7z=3
Доказать, что выполняется равенство для всех элементов поля
Нужна помощь в доказательстве. самого не выходит. Нужно доказать, что если выполняется равенство.
Доказать, что выполняется равенство для всех элементов поля
Здравствуйте! Задаче: Доказать, что если xn=x для всех элементов x поля K, то K конечно, и его.
Это одно из самых странных доказательств, которые я видел.
Доказательство утверждения, начинающегося с «Для любого x», начинается с «Рассмотрим произвольный x». Доказательство утверждения вида «Если A, то B», начинается с «Предположим A и докажем B».
А по сути здесь нужно выразить c через a и b и воспользоваться свойствами векторного произведения.
Признаки равенства треугольников
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Первый признак равенства треугольников
Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.
Давайте рассмотрим три признака равенства треугольников.
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
При наложении △A1B1C1 на △ABC вершина A1 совмещается с вершиной A, и сторона A1B1 накладывается на сторону AB, AC — на сторону A1C1.
Сторона A1B1 совмещается со стороной AB, вершина B совпадает с вершиной B1, сторона A1С1 совмещается со стороной AС, вершина C совпадает с вершиной C1.
Значит, происходит совмещение вершин В и В1, С и С1.
Второй признак равенства треугольников
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1, вершины В и В1 лежат по одну сторону от А1С1.
Тогда АС совмещается с A1C1, вершина C совпадает с C1, поскольку мы знаем, что АС = A1C1.
AB накладывается на A1B1, поскольку мы знаем, что ∠A = ∠A1.
CB накладывается на C1B1, поскольку мы знаем, что ∠C = ∠C1.
Вершина B совпадает с вершиной B1.
Третий признак равенства треугольников
Теорема 3. Равенство треугольников по трем сторонам.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство 3 признака равенства треугольников:
Приложим △ABC к △A1B1C1 таким образом, чтобы вершина A совпала с вершиной A1, вершина B — с вершиной B1, вершина C и вершина C1 лежат по разные стороны от прямой А1В1.
Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.
Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.
Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.
Доказать что равенство верно
Применяя метод математической индукции, доказать, что для любого натурального n справедливы следующие равенства:
а) ;
б) .
а) При n = 1 равенство справедливо. Предполагая справедливость равенства при n, покажем справедливость его и при n + 1. Действительно,
что и требовалось доказать.
б) При n = 1 справедливость равенства очевидна. Из предположения справедливости его при n следует
т. е. утверждение справедливо и при n + 1.
Пример 1. Доказать следующие равенства
Решение. a) При n = 1 равенство примет вид 
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
Используя предположение индукции, получим
Таким образом, P(n + 1) истинно и, следовательно, требуемое равенство доказано.
Замечание 3. Этот пример можно решить (аналогично предыдущему) без использования метода математической индукции.
c) При n = 1 равенство истинно: 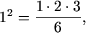
d) При n = 1 равенство справедливо: 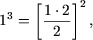
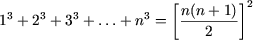
e) Утверждение P(1) справедливо: 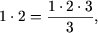
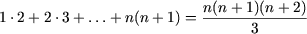
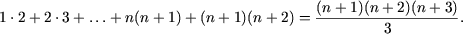
Следовательно, исходное равенство имеет место для любого натурального n.
f) P(1) справедливо: 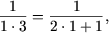
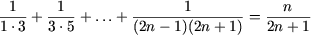
Действительно, учитывая, что P(n) имеет место, получим
Таким образом, равенство доказано.
g) При n = 1 имеем a + b = b + a и, следовательно, равенство справедливо.
Пусть формула бинома Ньютона справедлива при n = k, то есть,
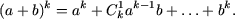
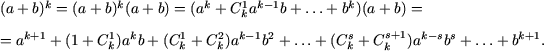
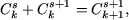
Пример 2. Доказать неравенства
Решение. a) При n = 1 получаем истинное неравенство
Таким образом, если P(n) истинно, то и P(n + 1) истинно, следовательно, согласно принципу математической индукции, неравенство Бернулли справедливо.
Рассмотрим следующие два случая:
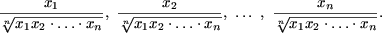
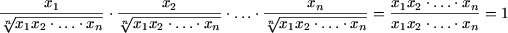
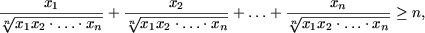
sin 2n a + cos 2n a ≤ 1 и покажем, что имеет место P ( n + 1). Действительно, sin 2(n + 1) a + cos 2(n + 1) a = sin 2n a ·sin 2 a + cos 2n a ·cos 2 a 2n a + cos 2n a ≤ 1 (если sin 2 a ≤ 1, то cos 2 a 2 a ≤ 1, то sin 2 a n О N sin 2n a + cos 2n ≤ 1 и знак равенства достигается лишь при n = 1.
e) При n = 1 утверждение справедливо: 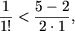
Допустим, что 
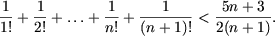
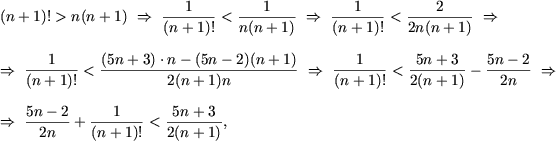
Поскольку при n > 10 имеем 
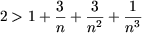
Пример 3. Доказать, что для любого n О N

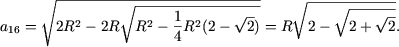
 | (2) |
Как ранее было показано при n = 1, что эта формула справедлива. Пусть (2) выполняется при n = k. Вычислим 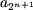
Замечание. Из (2) следует, что длина окружности равна
I. Доказать равенства
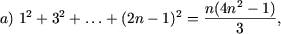 |
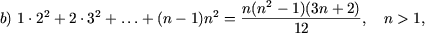 |
 |
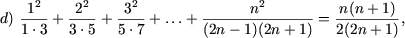 |
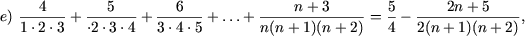 |
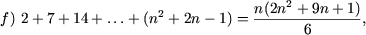 |
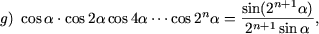 |
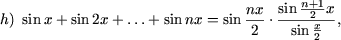 |
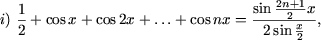 |
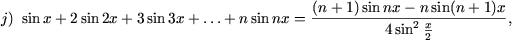 |
 |
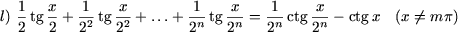 |
 |
II. Доказать неравенства
III. Доказать, что при любом натуральном n число an делится на b
IV. Показать, что 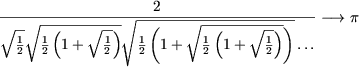
VI. Пусть даны n произвольных квадратов. Доказать, что эти квадраты могут быть разрезаны так, чтобы из получившихся частей можно было образовать квадрат.