Доказать что существует единственное линейное преобразование трехмерного пространства

Доказать, что преобразование трехмерного пространства является линейным преобразованием

Докажите, что данный геометрический оператор пространства R^3 является линейным
Найдите: 1) область значений и ранг, ядро и дефект этого оператора, исходя из геометрических.

Доказать, что множество векторов является линейным пространством
Доказать что множество n-мерных векторов, у которых координаты с нечетными номерами равны между.

Доказать, что функционал является линейным и непрерывным
Доказать, что функционал x=x(t)->\int_<0>^ <1>x(t)dt, в L1 является линейным и непрерывным, и.

Доказать, что функционал является линейным и непрерывным
Ребят, помогите решить задачу: Доказать, что функционал f: _ <2>\rightarrow C является.

Доказать, что оператор является линейным ограниченным
В пространстве C рассмотрим подпространство M функций x(t), удовлетворяющих условию x(-\pi)=x(\pi).

Доказать, что функционал является линейным непрерывным, и найти его норму
f (x) =\sum\limits_^\infty\frac, x=(x_1, x_2. )\in l_1 норма в l_1.

Доказать что функционал является линейным, ограниченным и найти его норму
Ребят, помогите пожалуйста с решением Доказать что функционал f:C->R f(x)=x(1/2) является.

Определить, является ли W линейным подпространством пространства V
помогите, что надо делать? Определить, является ли W линейным подпространством пространства V, и.

Источник

28. Линейные преобразования линейного пространства

Определение 35. Линейным преобразованием Линейного пространства называется линейный оператор данного линейного пространства самого в себя.

Всё, что было сказано о линейных операторах, очевидно, верно и для линейных преобразований, но некоторые формулы будут иметь более простой вид. Напомним формулы.

А = ,

Столбцы которой – координаты образов базисных векторов Е.

(35)

3. Связь столбцов координат вектора и его образа: Х1 = А×Х (36)

Определение 36. Квадратные матрицы А И В Называются Подобными, если существует такая квадратная невырожденная матрица С, что В = С–1×А×С.

5. Матрицы, задающие линейное преобразование в разных базисах, подобны.

6. Теорема 35. Для любых двух подобных матриц А И В Одного и того же порядка N Над полем Р и любого линейного пространства Ln над полем Р в Ln существуют такие базисы Е И Е1, что данные матрицы будут задавать в этих базисах одно и то же линейное преобразование.

Доказательство. Пусть В = С–1×А×С. Зафиксируем в Ln какой-нибудь базис. Матрица А В этом базисе задаёт линейное преобразование (пусть это J). Так как матрица С Невырожденная, то С–1 Может быть матрицей перехода. Пусть Е1 = Е×С–1. Тогда преобразование J в базисе Е1 Будет иметь матрицу С–1×А×(С–1 )–1 = С–1×А×С = В.

9. Пространство Ln* изоморфно линейному пространству квадратных матриц порядка N с элементами из поля Р. Следовательно, dim (Ln* ) = N2.

Источник

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Линейный оператор

Примеры линейных операторов

Бóльшую часть примеров пункта ☞ ПРИМЕРЫ ЛИНЕЙНЫХ ОТОБРАЖЕНИЙ представляют именно линейные операторы. Укажу еще несколько, к которым буду часто обращаться.

Пример 4. Задачу интерполяции можно интерпретировать как построение некоторого отображения. В интерполяционной таблице

По аналогии с задачей алгебраической интерполяции, можно поставить и задачу тригонометрической интерполяции. Имеем здесь «точку входа» в теорию дискретного преобразования Фурье. ♦

Основные определения

Теорема 2. Имеет место равенство:

Не всякий оператор обратим.

Показать, что обратным для оператора

Сформулируем еще один результат, являющийся частным случаем приведенного в пункте ☞ СВОЙСТВА ЛИНЕЙНЫХ ОТОБРАЖЕНИЙ.

Матрица оператора

Как изменяется матрица оператора при переходе к новому базису?

Доказательство ☞ ЗДЕСЬ.

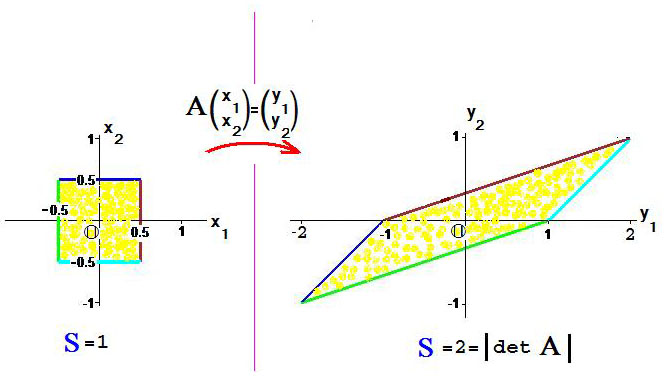
Иными словами: «физический» смысл определителя оператора заключается в том, что модуль его значения представляет коэффициент расширения 4) объема (в настоящем примере — площади) тела (соответственно, плоской фигуры) под воздействием этого оператора.

Теорема 5. Оператор обратим тогда и только тогда, когда когда его определитель отличен от нуля.

Теорема 7. В любом базисе пространства

б) матрица произведения операторов совпадает с произведением матриц этих операторов 5) ;

в) коммутирующим операторам соответствуют коммутирующие матрицы;

Матрица оператора и матрица перехода от базиса к базису

«Физический» смысл этих понятий различен. Образно говоря, если рассматривать оператор как процесс (точнее: установленную связь между входными и выходными значениями процесса), то выбор базиса можно интерпретировать как выбор точки зрения на этот процесс (можно трактовать эти слова как формализацию выражения «рассмотрим этот процесс под другим углом»).

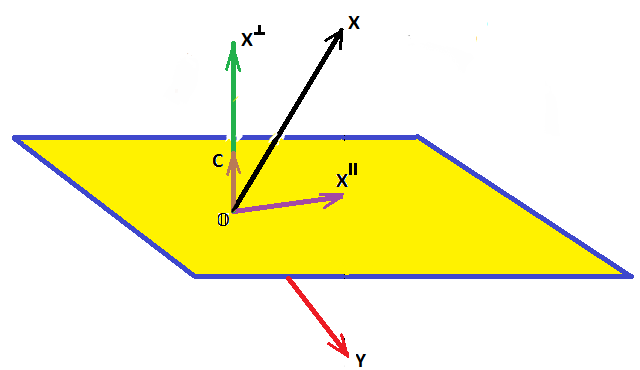
Матрица оператора проецирования

Настоящий пункт может быть пропущен при первоначальном чтении.

Матрица оператора отражения (оператора Хаусхолдера)

Настоящий пункт может быть пропущен при первоначальном чтении.

Инвариантное подпространство

Нас будут интересовать нетривиальные инвариантные подпространства.

Пример. Оператор

Пример. Оператор

Доказать, что сумма двух инвариантных подпространств является инвариантным подпространством.

Собственное число и собственный вектор

Задача. Найти одномерные инвариантные подпространства оператора.

Пример. Оператор

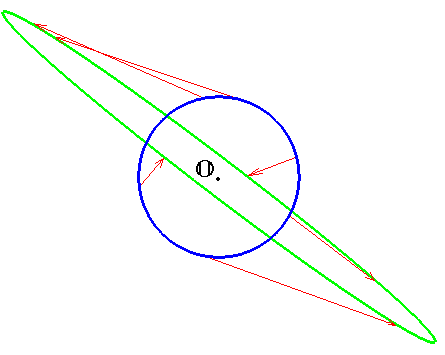
Анимация процесса ☞ ЗДЕСЬ (1500 Kb, gif).

Теорема. Любой собственный вектор оператора порождает его одномерное инвариантное подпространство, и обратно: любой ненулевой вектор одномерного инвариантного подпространства оператора является собственным вектором.

Задача. Для произвольного оператора выяснить условия существования его собственного числа и разработать конструктивный метод его нахождения.

Теорема. В комплексном линейном пространстве любой оператор имеет по крайней мере один собственный вектор.

Пример. Применим полученный результат для получения альтернативного решения предыдущего примера.

Теорема. Характеристические полиномы подобных матриц одинаковы.

Теорема [Гамильтон, Кэли]. Результатом подстановки оператора в собственный характеристический полином будет нулевой оператор.

Пример. Для рассмотренного в предыдущих примерах оператора

Диагонализуемость матрицы оператора

Теорема 1. Собственные векторы оператора, принадлежащие различным собственным числам, линейно независимы.

Теорема позволяет сформулировать достаточное условие диагонализуемости.

Теорема 3. Если характеристический полином оператора не имеет кратных корней, то матрица оператора диагонализуема.

В случае наличия у характеристического полинома оператора кратного корня, анализ оператора на возможность диагонализуемости его матрицы усложняется.

Теорема 5. Матрица оператора диагонализуема тогда и только тогда, когда для каждого ее собственного числа алгебраическая кратность равна геометрической кратности:

Диагонализуемость матрицы оператора над полем вещественных чисел

Жорданова нормальная форма

Задачи

Источники

[1]. Гантмахер Ф.Р. Теория матриц. 4-е изд. М.Наука. 1988.

[2]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ.1960

[3]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989

[4]. Мишина А.П., Проскуряков И.В. Высшая алгебра. М.Наука. 1965

Источник