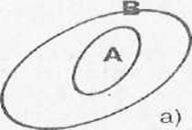
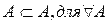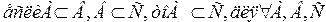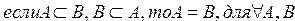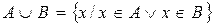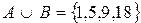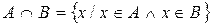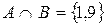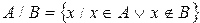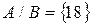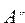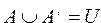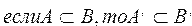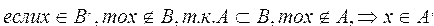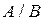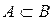Доказать что существует только одно пустое множество

Множество и его элементы. подмножество. пустое множество.

Понятие множества – одно из основных понятий математики. Под множеством понимают совокупность объектов (предметов или понятий), которая рассматривается как единое целое. Например, можно говорить о множестве натуральных чисел, о множестве букв на данной странице, о множестве корней данного уравнения и т. п. Понятие множества принимается как исходное, первичное, т. е. несводимое к другим понятиям. Объекты, входящие в состав множества, называются его элементами. Обычно множества обозначаются большими печатными буквами английского алфавита, например, множество А; а его элементы маленькими прописными буквами, например, элемент а.

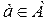
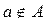
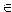
Запись означает, что элемент а принадлежит множеству А. Запись — наоборот, Что элемент а множеству А не принадлежит. Знак называют знаком принадлежности.

Определение 1. Два множества А и В называются равными и пишут А=В, если множества А и В содержат одни и те же элементы.

Например: <2, 4, 6>= <4, 2, 6>– равные множества.

Определение 2. Множество называется непустым, если содержит хотя бы один элемент.

Определение 3. Множество А является подмножеством множества В, если каждый элемент множества А принадлежит множеству В.

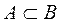
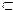
В этом случае пишут , знак называют знаком включения.

Например: <2, 4,>

Рассмотрим свойства отношения включения.

рефлексивно, т.е любое множество является подмножеством самому себе.

транзитивно, т. е. для любых множеств А, В и С, если множество А является подмножеством множества В и множество В является подмножеством множества С, то из этого следует, что множество А является подмножеством множества С.

антисимметрично, т. е. для любых множеств А и В следует, что, если множество А является подмножеством множества В и в то же время множество В является подмножеством множества А, то множества А и В равны.

Определение 4. Множество, не содержащее ни одного элемента, называется пустыммножеством.

Пустое множество обозначают

Пустое множество является подмножеством любого множества.

Определение 5. Множество всех подмножеств множества A называется множеством-степенью и обозначается P(A).

В дальнейшем будем пользоваться следующим утверждением:

Утверждение 1. Число всех подмножеств конечного множества равно 2n.

Пример. Выделим все подмножества множества А =<2, 4, 6>.

Р(А)=<2, 4, 6>, <2, 4>, <4, 6>, <2, 6>, <2>, <4 >, <6>, — всего 23=8.

Операции над множествами

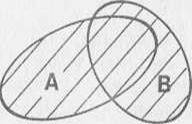
Объединением множеств А и В называется множество, состоящее из тех элементов, которые принадлежат одному из множеств А или В.

Для обозначения объединения множеств используют знак .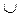

Пример. , ,

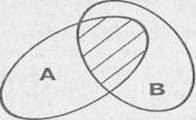
Пересечением множеств А и В называются такое множество, элементы которого принадлежат как множеству А, так и множеству В.

Для обозначения пересечения множеств используют знак .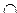

Пример. , ,

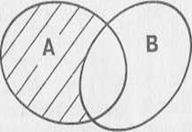
Разностью множеств А и В называется множество, элементы которого являются элементами множества А, не принадлежащие множеству В.

Для обозначения разности множеств используют знак /.

Пример. , ,

Перечислим основные свойства операций над множествами:

1) идемпотентность объединения

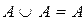
2) идемпотентность пересечения

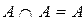
3) коммутативность объединения

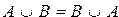
4) коммутативность пересечения

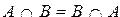
5) ассоциативность объединения

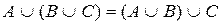
6) ассоциативность пересечения

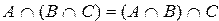
7) дистрибутивность объединения относительно пересечения

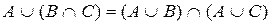
8) дистрибутивность пересечения относительно объединения

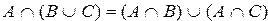
Универсальное множество. Дополнение множества.

Во многих приложениях теории множеств рассматриваются только такие множества, которые содержатся в некотором фиксированном множестве. Например, в геометрии мы имеем дело с множеством точек данного пространства, в арифметике – с множеством целых чисел. Такое фиксированное множество называют универсальным.Для его обозначения используют букву U.

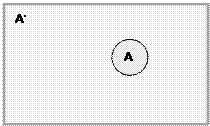
Определение 6. Множество U/А называется дополнением множества А и обозначается (или ).

Дополнение U/ множества обозначается

Справедливы следующие формулы:

=

— закон инволюции.

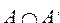
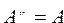
Теорема. Если множество А является подмножеством множества В, то дополнение множества А будет являться подмножеством дополнения множества В.

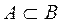
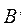
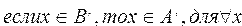
Пусть множество А является подмножеством множества В, , необходимо доказать, что для каждого элемента х из универсального множества U выполняется следующее условие: если элемент х принадлежит множеству , то он принадлежит и множеству .

.

Действительно, если х принадлежит множеству , то он не принадлежит множеству В, а т. к. множество А является подмножеством множества В, то элемент х не принадлежит и множеству А, а это означает его принадлежность множеству .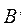

Теорема. Имеют место следующие тождества

— Законы де Моргана для множеств

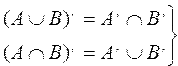
Приведем краткое доказательство первого утверждения.

Второе утверждение докажите самостоятельно.

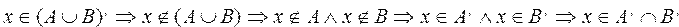
Для графического изображения множеств и их свойств используются так называемые диаграммы Эйлера-Венна.

Объединение множеств Пересечение множеств

Разность множеств Подмножество

Универсальное множество Дополнение

Понятие множества. Элементы множества. Пустое множество. Принадлежность элементов.

Источник

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

пустое множество

Заслуженный участник

Заморожен

Заморожен

О, да. Оно единственно и было вначале. Все остальные множества произошли из него.

И сдаётся мне, что у Цермело и Френкеля теология крепко в башке сидела. А вообще, всю современную математику придумали средневековые схоласты.

Заслуженный участник

Заморожен

Добавлено спустя 2 часа 37 минут 17 секунд:

Подумал вот, что «ничего» тоже разное бывает.

Заслуженный участник

Как некоторое следствие этого ( точнее сказать не могу, я «для себя» это доказывал от противного ) идет широко используемое в трудах Бурбаки соотношение, что пересечение пустого семейства подмножеств множества X будет совпадать с X.
( Напротив, объединение пустого семейства подмножеств будет пустым множеством. )

За счет этого, например, три традиционные аксиомы открытой топологии сводятся к двум симпатично-двойственным. Так же несколько упрощаются вроде бы какие-то определения фильтров, хотя точно уже не помню.

Заморожен

Так это же просто по определению пересечения! Определение есть определение, точнее уже некуда.

Определение: Для

Посмотрите сами, что за множество получается справа при .

Добавлено спустя 3 минуты 19 секунд:

Заслуженный участник

Неравенства вроде и то естественнее, от противного доказываются вроде бы нормально. А какие-то еще подобные особенности есть?

Заморожен

А то, что инфимум больше супремума, Вас не удивляет?

Последний раз редактировалось Spook 11.06.2008, 14:11, всего редактировалось 1 раз.

Ну ведь это просто отображение . Оно одно. А вот с арифметическими операциями c точки зрения множеств уже не так все ясно. Даже для простейших из них, например , хотя они должны доказываться «на низком уровне».

Добавлено спустя 29 секунд:

Заслуженный участник

Т.е. в данном случае интересует множество отображений из пустого множества в пустое, которое состоит из единственного «пустого» отображения.

Добавлено спустя 22 минуты 5 секунд:

Заморожен

Это получается непосредственно из определений.

Пусть — некоторое частично упорядоченное множество. Вспомним определения.

1) Для элемент называется наименьшим (в ), если .

2) Для элемент называется верхней гранью для , если . Множество всех верхних граней для обозначаем .

3) Для если в множестве есть наименьший элемент, то он называется супремумом и обозначается .

Ну а теперь возьмём . Согласно второму определению

Значит, — это наименьший элемент в . Аналогично есть наибольший элемент в .

Добавлено спустя 2 минуты 46 секунд:

Добавлено спустя 1 минуту 16 секунд:

Т.е. в данном случае интересует множество отображений из пустого множества в пустое, которое состоит из единственного «пустого» отображения.

Возникает вопрос: если на «низком уровне» доказано, что , то как это сочетается с тем, что не определен, а значит и не определен?

Заслуженный участник

Правильно .

Вообще говоря, тот факт, что , никакого отношения к теории пределов не имеет, поскольку в теории пределов используются свои собственные определения.
Что касается конкретного предела , то он благополучно равен . Но предел вида , если и , может иметь любое конечное или бесконечное значение или вообще не существовать.

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Источник