Датчик сконструирован таким образом что

Датчик сконструирован таким образом

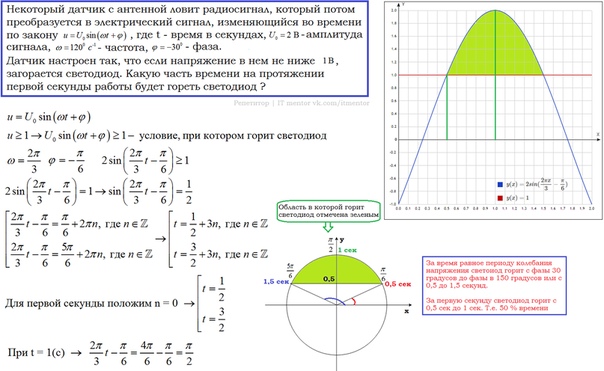
28000. Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону

t — время в секундах амплитуда U₀ =2В

частота ω = 120 0 с –1 фаза φ = –30 0

Датчик настроен так, что если напряжение в нём не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть.

Определим продолжительность горения лампочки. Для того, чтобы она горела напряжение должно быть равно или более 1 В. Решаем неравенство:

В условии речь идёт об амплитузе и частоте, кроме этого нет никаих ограничений для угла, стоящего под знаком синуса, поэтому необходимо учесть периодичность синуса.

Получили, что сигнал имеет периодичность в три секунды. Так как нас интересует первая секунда (из условия), то рассмотрим неравенство при n = 0:

Значит лампочка загорится через 0,5 секунды и погаснет через 1,5 с момента начала работы датчика. На протяжении первой секунды лампочка будет гореть половину секунды, то есть 50% времени.

*Примечание! При n = – 1 время получится отрицательным, поэтому это значение мы не рассматриваем.

28001. Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону

t — время в секундах амплитуда U 0 =2В

частота ω = 240 0 с –1 фаза φ = –120 0

Датчик настроен так, что если напряжение в нём не ниже чем 1 Вольт, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть.

Определим продолжительность горения лампочки. Для того, чтобы она горела напряжение должно быть равно или более 1 Вольт. Решаем неравенство:

В условии речь идёт об амплитузе и частоте, кроме этого нет никаих ограничений для угла, стоящего под знаком синуса, поэтому необходимо учесть периодичность.

Получили, что сигнал имеет периодичность в 1,5 секунды. Так как нас интересует первая секунда (сказано условии), то рассмотрим неравенство при n = 0:

Значит лампочка загорится через 0,625 секунды и погаснет через 1,125 с момента начала работы датчика. На протяжении первой секунды лампочка будет гореть 1 – 0,625= 0,375 секунды, то есть 37,5% времени.

*Примечание! При n= –1 время получится с отрицательным знаком, поэтому отрицательные значения n не рассматриваем. Но обращать на это внимание необходимо. Например, если мы в подобной задаче при n= –1 получим:

То что это будет означать, что лампочка будет гореть первые 0,25 секунды, потом погаснет и загорится через 0,75 после начала работы датчика. То есть в данном случае n= –1 «игнорировать» нельзя. Помните об этом!

Источник

Решение №800 Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется …

Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону U = U₀sin(ωt + φ), где t – время (в секундах), амплитуда напряжения U₀ = 2B, частота ω = 2π/3, фаза φ = π/12. Датчик настроен так, что если напряжение U в нем не ниже чем 1 В, загорается лампочка. Какую часть времени, в процентах, на протяжении первой секунды после начала работы лампочка будет гореть?

Вместо U подставим 1 В, найдём когда загорится лампочка:

Лампочка загорится в 0,125 с. и будет продолжать гореть до 1 с. т.к. напряжение будет расти.
Всего за первую секунду лампочка будет гореть:

1 – 0,125 = 0,875 с

Что будет равняться 87,5 % времени.

Источник

Датчик сконструирован таким образом что его антенна ловит радиосигнал который затем преобразуется

Реальная математика (2 уровень)

Прототип задания 11 (№ 28000)

$$U_0 \sin (\omega t + \varphi ) = 1,$$

Лампочка будет гореть 50% времени.

Прототип задания 11 (№ 28002)

Очень лeгкий заряженный металлический шарик зарядом \(q = 2 \cdot 10^<-6>\) Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет v = 5 м/с, на него начинает действовать постоянное магнитное поле, вектор индукции B которого лежит в той же плоскости и составляет угол \alpha с направлением движения шарика. Значение индукции поля \(B = 4 \cdot 10^<-3>\) Тл. При этом на шарик действует сила Лоренца, равная \(F_<\text<л>> = qvB\sin \alpha\) (Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла \(\alpha \in \left\) шарик оторвeтся от поверхности, если для этого нужно, чтобы сила \(F_<\text<л>>\) была не менее чем \(2 \cdot 10^<-8>\) Н? Ответ дайте в градусах.

$$qvB\sin \alpha \ge 2 \cdot 10^<-8>,$$

$$ 2\cdot 10^ <-6>\cdot 5 \cdot 4 \cdot 10^ <-3>\sin \alpha \ge 2 \cdot 10^<-8>,$$

Учитывая, что \(\alpha \in \left\) и нам нужно наименьшее значение угла, то

Прототип задания 11 (№ 28003)

Небольшой мячик бросают под острым углом \(\alpha\) к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой \(H=\frac<><<4g>>(1 — \cos 2\alpha )\), где \(v_0 = 20\) м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте g=10 м/с\(<>^2\)). При каком наименьшем значении угла \(\alpha\) (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?

$$10(1 — \cos 2\alpha) = 5,$$

Прототип задания 11 (№ 28004)

Небольшой мячик бросают под острым углом \(\alpha\) к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле \(L=\frac<>\sin 2\alpha\) (м), где \(v_0=20\) м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте g=10 м/с\(<>^2\)). При каком наименьшем значении угла (в градусах) мячик перелетит реку шириной 20 м?

Источник

Репетитор по математике

Стоимость занятий

Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.

Видеокурсы подготовки к ЕГЭ-2021

Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.

Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.

Группа Вконтакте

В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.

Преимущества

Педагогический стаж

Собственная методика

За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.

Гарантированный результат

За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.

Индивидуальная работа

Источник