Деление на и деление по в чем разница
Задачи на деление по содержанию и деление на равные части
Урок 7. Решение текстовых задач по математике 1-4 классы
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Задачи на деление по содержанию и деление на равные части»
Сегодня на урок к нам пришли брат и сестра – Ваня и Таня. Мама принесла домой бананы и предложила им разделить бананы поровну между всеми членами семьи. Ваня с Таней не смогли этого сделать и чуть не подрались. Давайте поможем им, да и сами научимся делить всё поровну.
Итак, мама принесла домой 12 бананов. В семье 4 человека. По сколько бананов получит каждый?
Членов семьи четверо, значит надо разделить бананы на 4 равных части. Давайте посмотрим, как это можно сделать. Сначала дадим каждому по одному банану, потом ещё по одному, и ещё по одному. Все бананы раздали. Каждый получил по 3 банана.
А теперь всё, что мы делали, запишем с помощью чисел и математических знаков.
12 бананов разделили на четверых поровну, т.е. на 4, и получилось по 3 банана каждому. Так это же запись решения задачи. Осталось написать только ответ.
Ответ: по 3 банана получил каждый.
А теперь поможем ребятам решить ещё одну задачу.
На День рождения Таня испекла вкусный торт и разрезала его на 8 кусочков. Она хочет, чтобы каждый съел по 2 кусочка. Сколько человек получит по 2 кусочка?
Хватит ли всем членам семьи?
Таня раскладывает тортик по тарелочкам. На первую тарелочку кладём 2 кусочка. На вторую ещё 2 кусочка. На третью – 2, и на четвертую 2. Кусочки торта Таня разложила на 4 тарелочки – маме, папе, брату и себе. Всем хватило по 2 кусочка. А как это запишем при помощи чисел и знаков?
8 кусочков разложили по 2, т.е. поровну. А мы помним, что если раскладываем поровну, значит это действие деления. Получилось 4, т.е. тортик могут получить 4 человека. Записали решение, теперь можем записать ответ.
Итак, сегодня мы узнали, что если надо что-то раздать поровну, мы выполняем действие деления.
Деление на и деление по в чем разница
Можно заставить ребенка просто решать скучные примеры (и ему будет совсем неинтересно), а можно предложить ему решить забавные текстовые задачки в тетради Kumon или сразиться в межпланетном рыцарском турнире на звание лучшего знатока дробей. Второй подход определенно занимательнее: ребенку гораздо больше понравится учить математику в игре.
Ребятам постарше также по душе будут игровые моменты в обучении. Ведь гораздо веселее изучать математику через яркое домино, чем читать длинные главы в учебнике.
Подготовили для вас несколько советов и подборку книг, которые помогут разложить умножение и деление по полочкам.
Умножаем
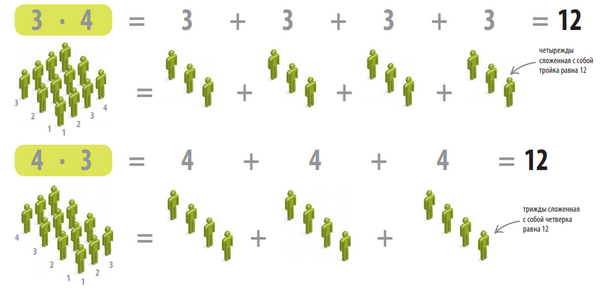
Что такое умножение? При умножении второе число показывает, сколько раз нужно сложить первое число с самим собой. На рисунке в каждой шеренге стоят 13 человек, а всего шеренг 9. Чтобы подсчитать общее количество людей, нужно число 13 сложить само с собой 9 раз. Это и будет произведением чисел 13 на 9.
Не имеет значения, в каком порядке перемножаются числа: ответ будет одинаковым. Ниже показаны два способа, как можно вычислить произведение.
Умножение на 10, 100, 1000 Для того чтобы умножить целое число на 10, 100, 1000 и т. д., нужно просто дописать справа от этого числа один нуль (0), два нуля (00), три нуля (000) и т. д.
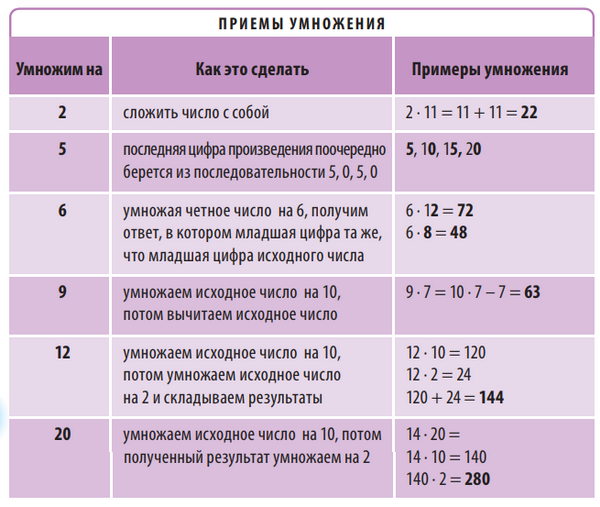
Приемы умножения. Некоторые числа легко умножать, зная особые приемы. В таблице показаны приемы быстрого умножения на 2, 5, 6, 9, 12 и 20.
Делим
Деление позволяет найти, сколько раз одно число содержится в другом. Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет. Или так: 10 монет, разложенные в стопки по 2 монеты, дадут 5 стопок.
Как выполняется деление? Деление одного числа (делимого) на другое (делитель) показывает, сколько делителей содержится в делимом. Например, при делении 10 на 2 мы находим, сколько чисел 2 содержится в числе 10. Результат деления называется частным.
Деление как распределение. Распределение чего-либо — это, по сути, операция деления. Так, если поровну распределить четыре конфеты между двумя людьми, у каждого из них будет по две конфеты.
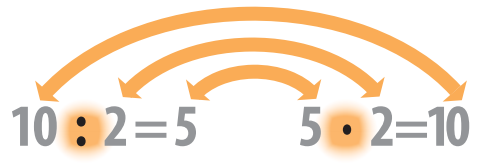
Как деление связано с умножением? Деление — это операция, обратная умножению. Если вы знаете результат деления, то можете записать соответствующее произведение, и наоборот.
Если 10 (делимое) поделить на 2 (делитель), то получится 5 (частное). Умножая частное (5) на делитель (2), мы получаем значение исходного делимого (10).
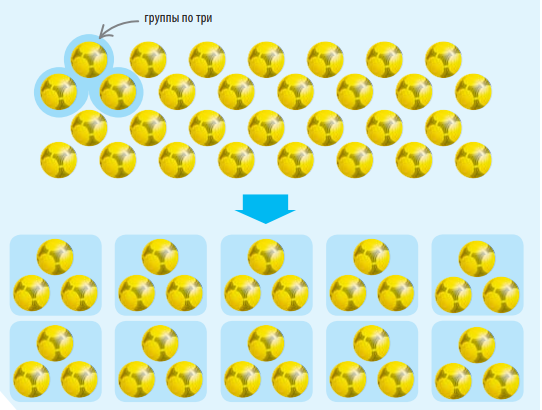
Другой подход к делению. Деление также показывает, сколько раз в делимом встречаются группы, равные делителю. Ответом будет то же самое частное. Получилось ровно 10 групп по 3 мяча (без остатка), поэтому 30 : 3 = 10. В этом примере 30 футбольных мячей делятся на группы по 3 мяча.
Книги и тетради, которые помогут закрепить навыки
Арифметикум

Домино, с которым ребенок научится хорошо складывать, вычитать, умножать и делить числа до 100. Игрок должен разместить карточку так, чтобы на оказавшихся рядом клеточках был написан пример и правильный ответ или два примера, в результате решения которых получится одно число.
Вокруг любой клеточки можно расположить сразу несколько карточек: по одной у каждой свободной стороны. Проверить вычисления игроки могут по цветным узорам: если узоры совпадают, ход сделан правильно.
Умножариум

Веселая игра поможет освоить математику
Это домино создано специально для легкого и увлекательного изучения таблицы умножения детьми: вместо традиционных точек на каждой карточке нанесены математические примеры и цифры. Совмещая клетку с примером (например, 5×8) и результат умножения (40), ребенок сразу видит, правильно ли он посчитал пример, благодаря цветовому паттерну, который должен совпасть на двух клетках.
Kumon спешит на помощь
У нас есть множество тетрадей разных уровней сложности, которые помогут выучить таблицу умножения на зубок.
KUMON. Математика. Умножение. Уровень 4
Эта яркая тетрадка научит ребенка умножать многозначные числа в столбик. Шаг за шагом он будет осваивать этот навык, его ждут примеры, которые будут постепенно усложняться, полезные подсказки и, конечно, ключи с ответами в конце тетради для самоконтроля.
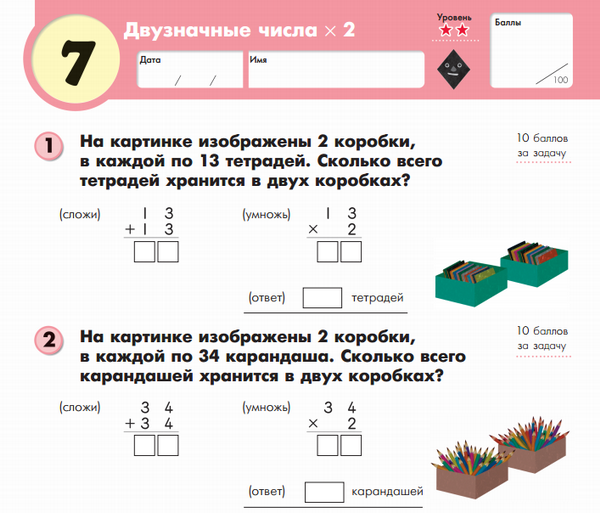
Простые задачки научат умножать. Пример из тетради
Kumon. Математика. Деление. Уровень 4
Выполняя задания в этой тетради, ваш ребёнок научится делить многозначные числа в столбик с остатком и без него. Продвигаясь вперёд небольшими последовательными шажками, он обретёт не только математические знания, но и уверенность в своих силах.
Межпланетный рыцарский турнир
Решая примеры из этой книги, ребенок примет участие в настоящем межпланетном состязании! Каждый правильный ответ — ты успешно атаковал противника, каждая ошибка — противник успешно атаковал тебя. Для убедительности в книге есть изображения персонажей, за которых нужно сыграть юному математику, и их соперников, а также фантастические истории про инопланетян. Всех героев можно раскрасить!
Логика: Шпаргалка (6 стр.)
17. ЛОГИЧЕСКАЯ ОПЕРАЦИЯ ДЕЛЕНИЯ ПОНЯТИЙ. ВИДЫ ДЕЛЕНИЯ
Логическая операция, раскрывающая объем понятия, называется делением. Деление позволяет выявить круг предметов, на которые распространяется данное понятие, это есть деление рода на виды. Родовидовые отношения характеризуются тем, что то, что можно сказать о роде, можно сказать и о виде. Так, понятие «конституция» можно разделить на конституцию федеративного государства и конституцию унитарного государства. Эти понятия обладают теми же признаками, которыми обладает родовое понятие.
Деление следует отличать от мысленного расчленения. Расчленение относится к взаимоотношению целого и части. Так, конституция расчленяется на статьи и параграфы, которые не обладают признаками понятия «конституция».
Деление необходимо в следующих случаях:
1) когда необходимо раскрыть не только сущность, но и формы ее проявления;
2) когда нужно очертить сферу применения понятия;
3) в случае многозначности термина.
Деление имеет свою структуру. В ней различаются:
• делимое – это родовое понятие, объем которого раскрывается через составляющие его виды (в нашем примере – это конституция);
• члены деления – полученные в результате самой операции виды родового понятия (конституция унитарного государства, конституция федеративного государства);
• основание деления – признак (или признаки), по которому производится эта операция (в нашем случае – это характер государственного устройства).
Различают два вида деления: по видоизменению признака и дихотомическое.
1 – деление по видоизменению признака, положенного в основание деления. Напр., всех людей можно разделить на группы по различным признакам: расовому, социальному, профессиональному, половозрастному, территориальному и др. В каждом из этих случаев члены деления будут разные. Этот вид деления часто применяется в науке и юридической практике. Однако недостаток этого вида деления в том, что объем делимого родового понятия может быть неисчерпаем.
2 – дихотомическое деление (от греч. слов dicha – на две части и tome – сечение) представляет собой деление объема делимого понятия на два противоречащихпонятия. Напр.: природа делится на живую и неживую, химические элементы на металлы и неметаллы и т. д. Достоинством этого вида деления является то, что объем делимого понятия исчерпывается полностью, а недостаток его в том, что область отрицательного понятия остается достаточно неопределенной.
Иногда используют смешанное деление. Напр., граждан делят на дееспособных и недееспособных, а затем дееспособные, в свою очередь, делятся на полностью и частично дееспособных.
18. ПРАВИЛА ДЕЛЕНИЯ
Как и определение, операция деления подчиняется особым правилам.
1. Деление должно вестись только по одному основанию. Это требование означает, что избранный вначале в качестве основания отдельный признак или совокупность признаков не следует в ходе деления подменять другими признаками. Правильно, напр., делить климат на холодный, умеренный и жаркий. Деление его на холодный, умеренный, жаркий, морской и континентальный будет уже неверным: вначале деление производилось по среднегодовой температуре, а затем – по влажности. Такая ошибка называется перекрестным или сбивчивым делением.
2. Деление должно быть соразмерным или исчерпывающим, т. е. сумма объемов членов деления должна равняться объему делимого понятия. Это требование предостерегает от пропуска отдельных членов деления. Если, напр., при делении преступлений в зависимости от характера и степени общественной опасности выделить преступления небольшой тяжести, средней тяжести и тяжкие преступления, то правило соразмерности будет нарушено, т. к. не указан еще один член деления – особо опасные преступления. Такое деление называется неполным.
Правило соразмерности будет нарушено и в том случае, если будут указаны лишние члены деления, т. е. понятия, не являющиеся видами данного рода. Напр., если при делении понятия «уголовное наказание» кроме всех видов указывается предупреждение, которое не входит в перечень мер наказания в уголовном законодательстве, а является видом административного взыскания, то это будет ошибкой, которая называется делением с лишними членами.
3. Члены деления должны исключать друг друга.
Они могут быть лишь несовместимыми, соподчиненными понятиями. Напр., неправильными являются деления: ученики делятся на отличников, неуспевающих и успевающих, т. к. понятия отличник и успевающий не исключают друг друга; преступления делятся на умышленные, неосторожные и воинские, т. к. воинские одновременно могут быть или умышленными, или неосторожными.
4. Деление должно быть последовательным и непрерывным. От рода следует переходить к ближайшим видам, а затем от них – к ближайшим подвидам. Если это правило нарушается, возникает логическая ошибка – скачок в делении. Так, если право мы сначала разделим на отрасли – трудовое, уголовное, гражданское, а затем гражданское – на право собственности, обязательственное право, наследственное право, то это правильное, последовательное и непрерывное деление. Но если после трудового, уголовного сразу назвать наследственное право, то это и будет означать скачок в делении.
19. КЛАССИФИКАЦИЯ. СУЖДЕНИЕ: СУЩНОСТЬ И РОЛЬ В ПОЗНАНИИ
Классификация – это особого вида деление, представляющее собой распределение предметов по группам (классам), при котором каждый класс имеет свое постоянное, определенное место. Классификация отличается рядом свойств.
• Это деление или система последовательных делений, которые произведены с точки зрения признаков, существенных для решения теоретической и практической задачи. Напр., на основе атомного веса создана периодическая система элементов Менделеева. При проведении классификации важно учитывать ее цель, т. е. указывать, решению каких задач она способствует.
• При классификации нужно так распределить предметы по группам, чтобы по месту в классификации можно было судить об их свойствах (напр., по месту химического элемента в периодической системе Менделеева можно судить о его свойствах).
• Результаты классификации могут быть представлены в виде таблиц или схем.
Создавая классификации, важно учитывать их относительный характер, поскольку классификация часто может не учитывать переходных форм явления. Кроме того, она может устареть.
Кроме рассмотренной классификации, называемой научной, в повседневной жизни используется т. н. искусственная классификация, т. е. распределение предметов на классы по несущественным признакам, напр., распределение фамилий в алфавитном порядке.
Суждение – это форма мысли, посредством которой раскрывается наличие или отсутствие каких-либо связей и отношений между предметами.
Отличительный признак суждения – утверждение или отрицание чего-либо о чем-либо. Суждение может быть истинным или ложным. Истинность суждения определяется его соответствием действительности, оно не зависит от нашего отношения к нему и носит объективный характер. Истинность суждений о простейших житейских ситуациях очевидна и не требует специального исследования. В науке же на подтверждение или отрицание какого-либо суждения требовались годы напряженного труда. Это относится и к юридической практике.
В виде суждений формулируются все научные истины. Они служат также универсальной формой духовного общения между людьми, взаимообмена информацией. Форму суждения обычно принимают статьи нормативных актов, регулирующих поведение людей в обществе.
Всякое суждение выражается в предложении, но не всякое предложение является суждением. Суждением может быть предложение, сообщающее какую-либо информацию, характеризуемую как истинная или ложная, т. е. это может быть только повествовательное предложение.
Одно и то же суждение может быть выражено в разных предложениях. Напр., «Аристотель является основателем науки логики» и «Воспитатель А. Македонского является основателем науки логики».
В свою очередь одно и то же предложение может выражать разные суждения. Напр., предложение «Аристотель – основатель науки логики» может выражать следующие суждения: «Аристотель (а не кто-либо другой) является основателем науки логики»; «Аристотель является основателем (а не продолжателем) науки логики»; «Аристотель является основателем науки логики (а не физики или математики)».
Памятка «решение задач на деление по содержанию и на равные части»
Методика работы над задачами на деление.
Полное рассуждение ученика в процессе решения задач обоих видов.
Задача на деление по содержанию.
8 апельсинов разложили по 4 апельсина на каждую тарелку. Сколько потребовалось тарелок?
Мне известно, что 8 апельсинов разложили по 4 апельсина на каждую тарелку.
Надо узнать, сколько потребовалось тарелок.
Рисую и объясняю. Обозначу каждый апельсин кружком. Рисую 8 кружков, столько было всего апельсинов. Отсчитываю 4 кружка, ставлю черту, столько апельсинов на одной тарелке. Отсчитываю ещё 4 кружка, столько апельсинов ещё на одной тарелке. Все апельсины разложили (больше нет кружков). Разложили поровну по 4, буду делить. Запишу решение: 8 : 4 = 2 (т.)
Отвечаю на вопрос задачи. Потребовалось 2 тарелки.
Схематический рисунок: или схема:
8 : 4 = 2 (т.) 8 : 4 = 2 (т.)
Ответ: 2 тарелки потребовалось. Ответ: 2 тарелки потребовалось.
Задача на деление на равные части.
8 апельсинов разложили на 2 тарелки поровну. Сколько апельсинов на каждой тарелке?
Мне известно, что 8 апельсинов разложили на 2 тарелки поровну.
Надо узнать, по сколько апельсинов на каждой тарелке.
Рисую и объясняю. Обозначу каждый апельсин кружком, рисую 8 кружков. Столько было всего апельсинов. Рисую под ними две замкнутые линии, столько было тарелок. Размещаю по одному кружку в каждую замкнутую линию (тарелку) и т.д. Все апельсины разложили поровну, буду делить.
Запишу решение: 8 : 2 =4 (ап.)
Отвечаю на вопрос задачи. На каждой тарелке по 4 апельсина.
Схематический рисунок: или схема:
8 : 2 = 4 (ап.) 8 : 2 = 4 (ап.)
Ответ: по 4 апельсина на каждой тарелке. Ответ: по 4 апельсина на каждой тарелке.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Скоростное чтение
Курс повышения квалификации
Актуальные вопросы теории и методики преподавания в начальной школе в соответствии с ФГОС НОО
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-433626
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Минобрнауки обновит перечень специальностей высшего образования
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В Ленобласти педагоги призеров и победителей олимпиады получат денежные поощрения
Время чтения: 1 минута
В школах Тюмени запустят раздельный сбор отходов
Время чтения: 1 минута
Комиссия РАН призвала отозвать проект новых правил русского языка
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Задачи на деление.
Во 2-м классе дети знакомятся с задачами на деление.
Существует 2 вида деления:
1. Деление на равные части; 2. Деление по содержанию.
Как правило, названия видов деления не нужно запоминать детям, но суть этих действий НЕОБХОДИМО ПОНЯТЬ!
Тогда и ошибок при решении задач – не будет!
Рассмотрим более подробно каждый вид деления.
1 вид. Деление на равные части.
Например: часть 2 с. 91
Разбор:
а) 14 кг разложили поровну в 2 корзины, т.е. разложили на 2 равные части.
14 грибов : 2 корзины = 7 грибов
б) 10 яблок раздали поровну 5 ребятам, т.е. разделили на 5 равных частей:
10 яблок : 5 ребят = 2 яблока
в) 18 марок наклеили поровну на 9 конвертов, т.е. разделили на 9 равных частей:
18 марок : 9 конвертов = 2 марки
2 вид. Деление по содержанию.
Например: часть 2 с. 103
Разбор:
а) 12 картошек раздали по 2 картошки:
12 картошек : 2 картошки = 6 туристов
б) 18 шариков разложили по 9 шариков:
18 шариков : 9 шариков = 2 кучки
в) а морковки связали в пучки по n морковок:
а морковок : n морковок = (а : n) пучков
Обратим внимание на предлог ПО : деление ПО содержанию.
При этом наименование в делимом и в частном всегда – разные:
а) картошка – туристы;
б) шарики – пучки;
в) морковки – пучки.
Памятку «Задачи на деление» можно скачать.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 68