Деление по модулю что это
Mod и остаток — не одно и то же
Приготовьтесь, вас ждёт крайне педантичная статья, которая вполне может спасти вас на собеседовании или сэкономить несколько часов при вылавливании бага в продакшне!
Я сейчас активно работаю над вторым сезоном «Руководства для самозванца» и пишу о шифре RSA для SSH, который, очевидно, является самым загружаемым фрагментом кода в истории IT.
Хочется полностью разобраться в этой истории. Кто придумал этот шифр, как он работает, почему работает и будет ли работать в будущем. Сейчас я раскопал одну чертовски интересную историю. Я не криптоманьяк и вижу, как других буквально засасывает в эту область. Но мне это тоже интересно, потому что повсюду есть маленькие норки, а меня как сороку привлекают блестящие штучки в глубоких норках. Я также очень хорош в метафорах.
В любом случае: на прошлой неделе я узнал что-то странное и хочу поделиться: оказывается, mod и остаток от деления — не одно и то же. Действительно забавно то, что некоторые читатели при этих словах выпрыгивают со своих кресел и орут: «А ведь именно это я всегда пытался сказать вам и всем остальным!»
Позовите ребят из секты «mod не остаток»! Это для вас.
Что такое mod?
Я должен был изучить это, как и в прошлый раз, когда всплыла такая тема. Это одна из тех вещей, которые ты знаешь, но не запоминаешь. Когда вы применяете mod, то делите одно число на другое и берёте остаток. Итак: 5 mod 2 будет 1, потому что 5/2=2 с остатком 1.
Вот где мы попадаем в странную серую область.
Математика циферблата
Криптографам нравится эта идея, потому что они могут использовать деление с остатком с гигантскими простыми числами для генерации криптографических ключей. Это совсем другая история: если хотите прочитать об этом, то можете купить книгу или, ещё лучше, поддержать мои усилия написать её.
Впрочем, не будем отклоняться от темы.
Остатки и математика циферблата
Теперь переходим к сути: modulo и простой остаток одинаковы, когда числа положительны, но отличаются в случае отрицательных чисел.
Рассмотрим такую задачу:
JavaScript с этим согласен:
Google согласен с первым утверждением, но не согласен со вторым:
Ruby согласен с Google:
Во имя Дейкстры, что здесь происходит?
Вращение часов назад
Чтобы ответить на вопрос, следует понять разницу между остатком и modulo. Программисты объединяют эти операции, но не должны этого делать, потому что они дают одинаковый результат только в случае, если делитель (в нашем случае 12) положителен. Вы можете легко отправить баги в продакшн, если делитель отрицательный.
Но почему существует разница? Рассмотрим положительный делитель 19 mod 12 на часах:
Это известная вещь
Прежде чем назвать меня сумасшедшим и начать гуглить тему: это известный факт. На самом деле MDN (Mozilla Developer Network) даже дошла до того, чтобы назвать % операцией «остатка» (remainder), а не modulo:
Оператор remainder возвращает остаток от деления одного операнда на другой. Он всегда принимает знак делимого.
Вот что Эрик Липперт, один из богов C#, говорит о modulo в C#:
Однако это совсем не то, что оператор % реально делает в C#. Оператор % не является каноническим оператором modulus, это оператор остатка.
А как на вашем языке?
Ну и что?
Могу понять, если вы дочитали досюда, а теперь чешете голову и задаётесь вопросом, стоит ли беспокоиться. Думаю, что стоит по двум причинам:
Введение в модулярную арифметику
Для любой системы взаимно простых чисел p1, … pn, любое число X из диапазона [0; M), где M = p1*p2*…*pn взаимооднозначно представимо в виде вектора (a1, a2, …, an), где ai = X%pi (здесь и далее «%» — операция взятия остатка от целочисленного деления X на pi).
p1, … pn – модули системы
a1, a2, …, an – остатки (вычеты) числа по заданной системе модулей
Прямое преобразование
Прямое преобразование из позиционной системы счисления (обычно в двоичном виде) в систему счисления в остатках заключается в нахождении остатков от деления по каждому из модулей системы.
Пример: Пусть требуется найти представление числа X = 25 по системе модулей (3, 5, 7). X = (25%3, 25%5, 25%7) = (1, 0, 4).
Реализация нахождения вычета в микроэлектронике по заданному модулю строится на следующих свойствах вычетов:
(a+b) % p = (a%p + b%p)%p
(a*b) % p = (a%p * b%p)%p
Любое число X можно записать в виде X%p = (xn-1*2 n-1 + xn-2*2 n-2 + x0*2 0 )%p = ((xn-1)%p*2 n-1 %p) + ((xn-2)%p*2 n-2 %p) + … + x0%p)%p. Поскольку в данном случае xn-1, … x0 равны 0 или 1, то фактически нам требуется сложить вычеты вида (2 i %p).
Пример: пусть задано число 25 или в двоичной системе счисления 11001 и требуется найти остаток по модулю 7.
25%7 = (1*2 4 + 1*2 3 + 0*2 2 + 0* 1 + 1*2 0 )%7 = (2 4 %7 + 2 3 %7 + 1%7)%7 = (2 + 1 + 1)%7 = 4
Арифметические операции
Пример: пусть задана система модулей (3, 5, 7), то есть мы можем выполнять операции, результат которых не превышает 3*5*7 = 105. Умножим два числа 8 и 10.
8 = (8%3, 8%5, 8%7) = (2, 3, 1)
10 = (10%3, 10%5, 10%7) = (1, 0, 3)
8*10 = ((2*1)%3, (3*0)%5, (1*3)%7) = (2, 0, 3)
Проверяем
80 = (80%3, 80%5, 80%7) = (2, 0, 3)
Обратное преобразование
Способ, основанный на Китайской теореме об остатках, базируется на следующей идее:
X = (x1, x2, … xn) = (x1, 0, …, 0) + (0, x2, …, 0) + … + (0, 0, …., xn) = x1*(1, 0, …, 0) + x2*(0, 1, …, 0) + … + xn*(0, 0, …, 1).
То есть для обратного преобразования требуется найти систему ортогональных базисов B1 = (1, 0, …, 0), B2 = (0, 1, …, 0), …, BN = (0, 0, …, 1). Эти вектора находятся один раз для заданного базиса, а для их поиска требуется решить уравнение вида: (Mi*bi)%pi = 1, где Mi = M/pi, а bi – искомое число. В этом случае позиционное представление Bi = Mi*bi и
X = (x1*(M1*b1) + x2*(M2*b2) + … + xn*(Mn*bn))%M
Пример: пусть задана система модулей (3, 5, 7), найдем значения Mi и bi (0 b1 = 2
(21*b2)%5 = 1 => b2 = 1
(15*b3)%7 = 1 => b3 = 1
Теперь преобразуем какое-нибудь число в системе остаточных классов. Положим
X = (2, 3, 1) = (2*35*2 + 3*21*1 + 1*15*1)%105 = (140 + 63 + 15)%105 = 218%105 = 8
Минус этого метода заключается в том, что для обратного преобразования требуется умножение и сложение больших чисел (M1, …, Mn), а так же операция взятия остатка по модулю большого числа M.
«Деление» по модулю
Обычные арифметические операции по модулю выполняются не сильно сложнее — просто нужно брать модули и заботиться о переполнении. Например:
Но вот с делением возникают проблемы — мы не можем просто взять и поделить.
Через бинарное возведение в степень
Этот подход простой и быстрый, однако следует помнить, что он работает только для простых модулей.
Через расширенный алгоритм Евклида
Расширенный алгоритм Евклида можно использовать для решения в целых числах уравнений вида
Преимущества этого метода над возведением в степень:
Но лично автор почти всегда использует возведение в степень.
Упрощенная реализация
Сначала приведем реализацию, а потом поймем, почему она работает:
Докажем по индукции, что функция действительно возвращает обратный элемент.
Во втором случае проверим правильность формулы:
Предподсчет обратных элементов
Чаще всего нам нужно искать обратный элемент в контексте комбинаторики.
Например, особенно часто нужно считать биномиальные коэффициенты, для чего в свою очередь нужно уметь обращать факториалы:
Простой способ — это предпосчитать обычные факториалы и каждый раз вызывать inv один или два раза:
Однако это добавит лишний логарифм в асимптотику в нередком случае, когда какая-то комбинаторная формула лежит внутри горячего цикла. Поэтому имеет смысл предподсчитать и частые обратные элементы.
Обратные факториалы
Все остальные обратные факториалы можно таким же образом итеративно подсчитать из предыдущего.
Деление по модулю в Java
Ещё со школы мы знакомы с таким понятием как обычное деление:
Как работает оператор сложения, вычитания и т.д. наверняка Вы уже знаете. А вот за что отвечает деление по модулю поймёте буквально через пару минут. Немного терпения.
Давайте посмотрим на примерах как это работает.
Пример №1
Необходимо разделить 9 на 4, используя:
Логику работы оператора деления по модулю Вы уже поняли. Самое время попробовать запустить пример на своём компьютере:
Если Вы запустите этот код на своём компьютере, то в консоль будет выведено такое число:
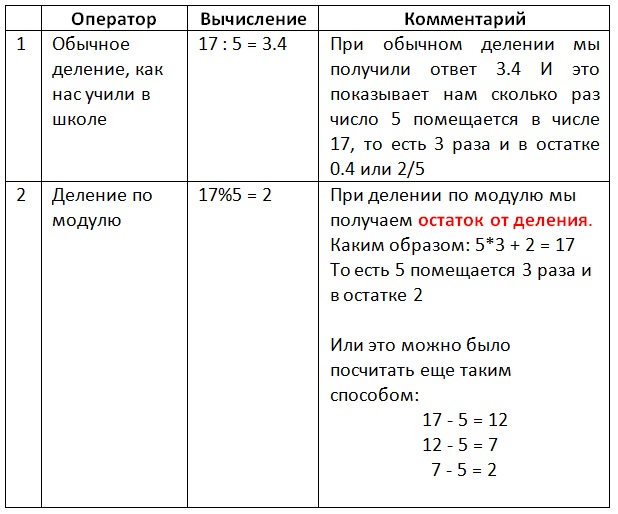
Пример №2
Необходимо разделить 17 на 5, используя:
И пробуем теперь запустить программу на компьютере:
Если Вы запустите этот код на своём компьютере, то в консоль будет выведено такое число:
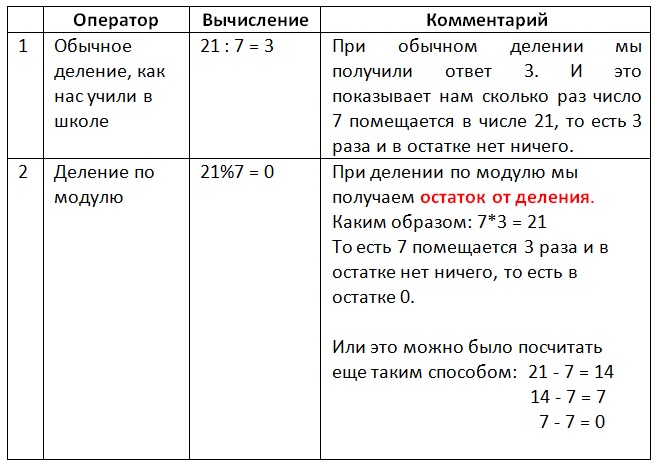
Пример №3
Необходимо разделить 21 на 7, используя:
И пробуем теперь запустить программу на компьютере:
Если Вы запустите этот код на своём компьютере, то в консоль будет выведено такое число:
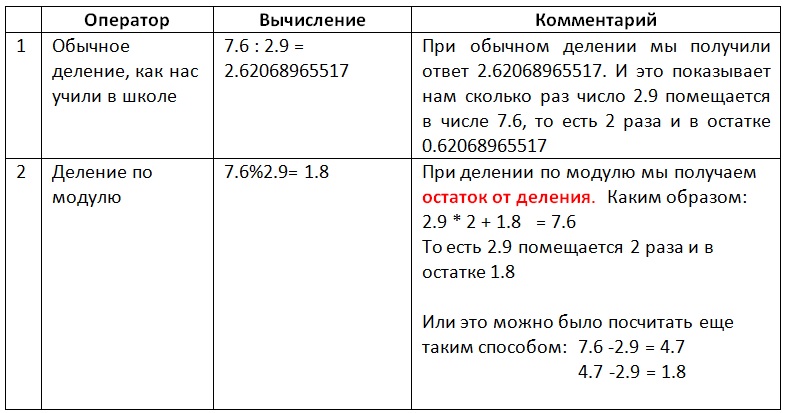
Пример №4
Необходимо разделить 7.6 на 2.9, используя:
И пробуем теперь запустить программу на компьютере:
Если Вы запустите этот код на своём компьютере, то в консоль будет выведено число, близкое к 1.8. Например, Вы можете увидеть какое-то такое число: 1.7999999999999998. Из-за определённых особенностей Java, которые мы будем с Вами рассматривать позже в других статьях, на разных компьютерах число будет немного отличаться. Но оно будет близкое по значению к 1.8
Итак, как Вы уже поняли, оператор деления по модулю вычисляет остаток от деления.
Есть небольшой нюанс при использовании оператора деления по модулю с отрицательными и положительными числами.
Работает простое правило:
Пример №5
Деление по модулю
Нахождение неполного частного также называют целочисленным делением, а нахождение остатка от деления называют взятием остатка или, неформально, делением по модулю (однако последний термин стоит избегать, так как он может привести к путанице с делением в кольце или группе вычетов по аналогии со сложением или умножением по модулю).
Операция деления с остатком может быть определена не только для целых чисел, но и для других математических объектов (например, для многочленов), см. ниже.
Содержание
Определение
Для отрицательного делителя нужно округлять частное в большую сторону:
Операция «mod» и связь со сравнениями
b.>
В программировании
| Язык | Неполное частное | Остаток | Знак остатка |
|---|---|---|---|
| ActionScript | % | Делимое | |
| Ada | mod | Делитель | |
| rem | Делимое | ||
| Бейсик | \ | MOD | Не определено |
| Си (ISO 1990) | / | % | Не определено |
| Си (ISO 1999) | / | % | Делимое [3] |
| C++ (ISO 2003) | / | % | Не определено [4] |
| C++ (ISO 2011) | / | % | Делимое [5] |
| C# | / | % | Делимое |
| ColdFusion | MOD | Делимое | |
| Common Lisp | mod | Делитель | |
| rem | Делимое | ||
| D | / | % | Делимое [6] |
| Delphi | div | mod | Делимое |
| Eiffel | // | \\ | Делимое |
| Erlang | div | rem | Делимое |
| Euphoria | remainder | Делимое | |
| Microsoft Excel (англ.) | QUOTIENT() | MOD() | Делитель |
| Microsoft Excel (рус.) | ЧАСТНОЕ() | ОСТАТ() | |
| FileMaker | Div() | Mod() | Делитель |
| Fortran | mod | Делимое | |
| modulo | Делитель | ||
| GML (Game Maker) | div | mod | Делимое |
| Go | / | % | Делимое |
| Haskell | div | mod | Делитель |
| quot | rem | Делимое | |
| J | | |
Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получения случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.
Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа. Например, в Паскале операция mod вычисляет остаток от деления, а операция div осуществляет целочисленное деление, при котором остаток от деления отбрасывается:
Знак остатка
Операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Тут есть два варианта:
Если в языке есть оба типа остатков, каждому из них соответствует своя операция неполного частного. Обе операции имеют жизненный смысл.
Как запрограммировать, если такой операции нет?
Обобщения
Вещественные числа
Деление 7,9 на 2,1 с остатком даёт: