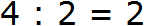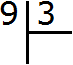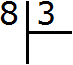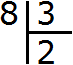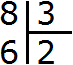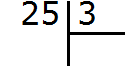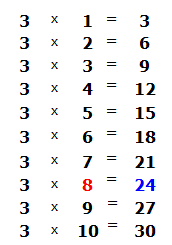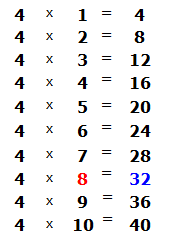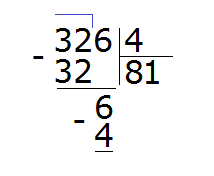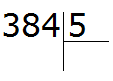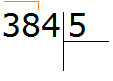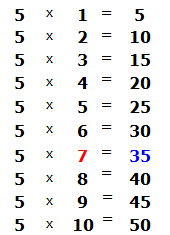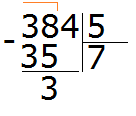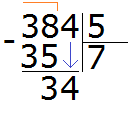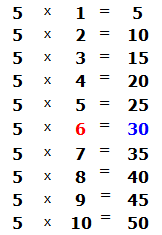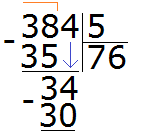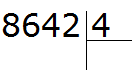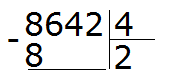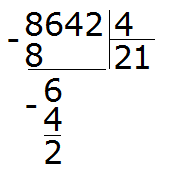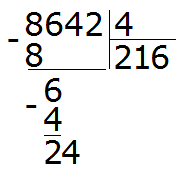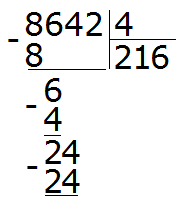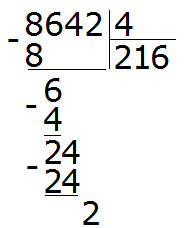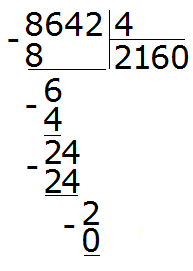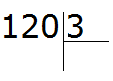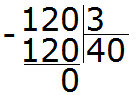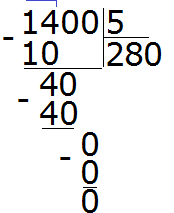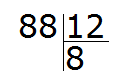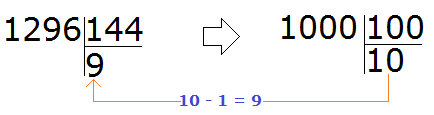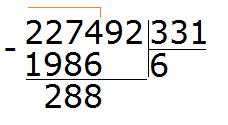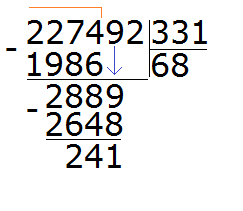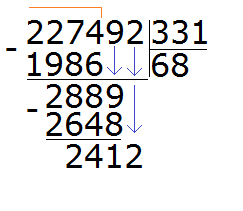Делимое чисел что это
Признаки делимости чисел
Что такое «признак делимости»
Признак делимости числа — это такая особенность числа, которая еще до выполнения деления позволяет определить, кратно ли число делителю.
Истинный путь джедая, чтобы зря не пыхтеть над числами, которые в конечном итоге не делятся.
Однозначные, двузначные и трехзначные числа
Однозначное число — это такое число, в составе которого один знак (одна цифра). Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные числа — такие, в составе которых два знака (две цифры). Цифры могут повторяться или быть различными.
Трехзначные числа — числа, в составе которых три знака (три цифры).
Чётные и нечётные числа
Число называют четным тогда, когда оно делится на два без остатка. А нечетные числа — те, что на два без остатка не делятся. Все просто!
Признаки делимости чисел
Признак делимости на 2. Сразу можно сказать, что число делится на 2, если последняя цифра четная.
Признак делимости на 3. Сумма цифр числа должна делиться на 3.
Признаки делимости на 4. Число делится на 4, если две последние цифры — 0 или если они образуют цифру, которая делится на 4.
Признаки делимости на 5. Число делится на 5, если заканчивается на 0 или 5.
Признак делимости на 6. На 6 делятся те числа, которые могут одновременно делится на 2 и на 3.
Признаки делимости на 8. Число делится на 8, если три последних цифры — 0 или если они образуют число, которое делится на 8.
Признак делимости на 9. Число делится на 9, если сумма цифр делится на 9.
Признаки делимости на 10, 100. Числа, которые заканчиваются на 0, 00, 000 делятся на 10, 100, 1000 и так далее.
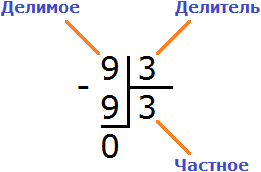
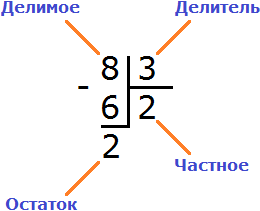
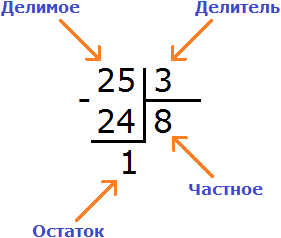
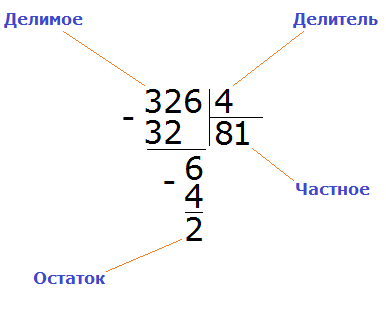
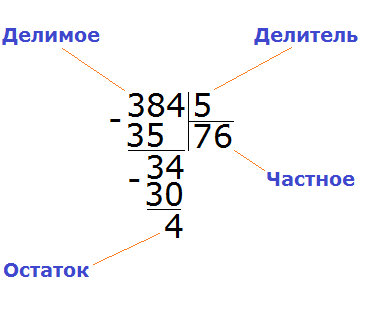
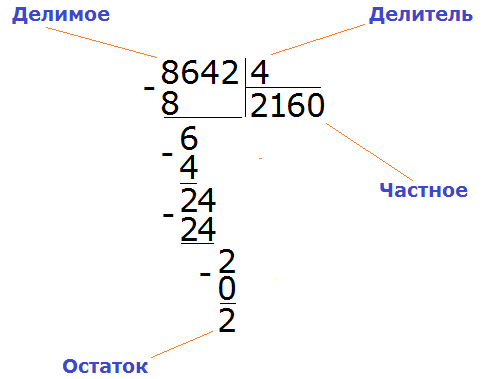
Делимое
Деле́ние (операция деления) — это одно из четырёх простейших арифметических действий, обратное умножению.
Подобно тому, как умножение заменяет неоднократно повторенное сложение, деление заменяет неоднократно повторенное вычитание.
Рассмотрим, например, такой вопрос:
сколько раз 3 содержится в 14?
Повторяя операцию вычитания 3 из 14, мы находим, что 3 «входит» в 14 четыре раза, и еще «остаётся» число 2
Результат деления также называют отношением.
Содержание
Деление натуральных чисел
Деление не замкнуто в кольце целых чисел. Простым языком это означает то, что деление одного целого числа на другое может не быть целым. В случае, если всё-таки результат является целым числом, говорят о делении без остатка.
Деление чисел издавна считалось самой трудной из арифметических операций. Было время, когда «секрет» деления знало не очень много посвящённых людей, и буквально передавало из поколения в поколение. Происходило это потому, что существовавшие алгоритмы деления были очень громоздки, сложны для исполнения и запоминания (например, деление в виде корабля). Появление деления столбиком радикально изменило эту ситуацию — теперь деление входит в раннюю школьную программу по математике наряду с остальными арифметическими действиями. Однако так же, как и в случае с умножением, в последнее время открыты более эффективные алгоритмы (см. en:Division (digital), применяющиеся в вычислительной технике.
Существуют правила, позволяющие быстро определить, делится ли число на заданный делитель без остатка (признаки делимости). Наиболее известные признаки делимости на 2, 3, 4, 5, 8, 9, 11, 25 и их производные, также существует признаки делимости на 7, 13, 1001 и другие числа.
Целое число, на которое одновременно делятся без остатка несколько чисел, называется их общим делителем.
Определение количества делителей натурального числа приводит к двум важным понятиям: составное и простое число. У простого числа есть только два делителя — 1 и само число.
В случае, если одно натуральное число не делится на другое без остатка, можно говорить о делении с остатком. Рассмотрение остатков, их сравнение и формализация в виде вычетов привели к целой науке — теории чисел.
Обычно на остаток накладываются следующие ограничения (чтобы он был корректно, т.е. однозначно, определён):
. 
.
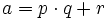
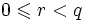
Деление целых чисел
Деление произвольных целых чисел не существенно отличается от деления натуральных чисел — достаточно поделить их модули и учесть правило знаков.
Однако деление целых чисел с остатком определяется по-разному. В одном случае, (так же как и без остатка) рассматривают сначала модули и в результате остаток приобретает тот же знак, что делитель или делимое (например, − 7 / ( − 3) = 2 с остатком (-1)); в другом случае понятие остатка напрямую обобщается и ограничения заимствуются из натуральных чисел:
.
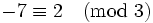
Деление рациональных чисел
Замыкание множества целых чисел по операции деления приводит к расширению его до множества рациональных чисел. Это приводит к тому, что результатом деления одного целого числа на другое всегда является рациональное число. Более того, полученные числа (рациональные) уже полностью поддерживают операцию деления (замкнуты относительно неё).
Правило деления обыкновенных дробей: 
Деление вещественных чисел
Деление также замкнуто в поле ненулевых вещественных чисел. Сечение Дедекинда позволяет однозначно определить результат деления.
Деление комплексных чисел
Комплексные числа опять замкнуты относительно операции деления.
Деление в алгебре
В отличие от простейших арифметических случаев на произвольных множествах и структурах деление может быть не только не определено, но и обладать множественностью результата.
Обычно в алгебре деление вводится через понятие единичного и обратного элементов. Если единичный элемент вводится однозначным образом (обычно аксиоматически или по определению), то обратный элемент часто может быть как левым ( x − 1 * x = e ), так и правым ( x * x − 1 = e ). Эти два обратных элемента могут по отдельности существовать или не существовать, равняться или не равняться друг другу.
К примеру, отношение матриц определяется через обратную матрицу, при этом даже для квадратных матриц может быть:
.
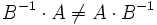
Отношение тензоров в общем случае не определено.
Деление многочленов
.
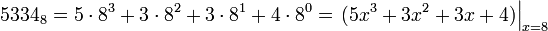
Поэтому аналогично определяются: частное, делитель, делимое и остаток (с той лишь разницей, что ограничение накладывается на степень остатка). Поэтому к делению многочленов также применимо деление столбиком.
Отличие же заключается в том, что при делении многочленов основной упор делается на степени делимого и делителя, а не на коэффициенты. Поэтому обычно считается, что частное и делитель (а следовательно и остаток) определены с точностью до постоянного множителя.
Деление на ноль
По правилам арифметики деление на число 0 запрещено, поскольку оно приводит к противоречию. Другое дело — деление на бесконечно малую функцию или последовательность (которые можно считать «нулями» в соответствующих множествах). Деление конечных функций на бесконечно малые приводит к появлению бесконечно больших, а отношение двух бесконечно малых называется неопределённостью 0/0, которую можно преобразовать (см. раскрытие неопределённостей) с тем, чтобы получить определённый результат.
Делимость чисел. Признаки делимости. Основная теорема арифметики
В этой статье – необходимая теория для решения задачи 18 Профильного ЕГЭ по математике. Но это не все. Знания о числах и их свойствах, признаки делимости и формула деления с остатком могут пригодиться вам при решении многих задач ЕГЭ.
Повторим еще раз, какие бывают числа.
Например, при делении 9 на 4 мы получаем частное 2 и остаток 1, то есть 9 = 4∙2 + 1.
Простые числа – те, что делятся только на себя и на единицу. Единица не является ни простым, ни составным числом. Простые числа: 2, 3, 5, 7, 11, 13, 17, 19…
Числа называются взаимно простыми, если они не имеют общих делителей, кроме 1.
Любое натуральное число можно разложить на простые множители.
Например, 72 = 2∙2∙2∙3∙3, а 98 = 2∙7∙7.
Основная теорема арифметики: Любое натуральное число можно представить в виде произведения простых делителей, взятых в натуральных степенях, причем это разложение единственно.
Наименьшее общее кратное двух чисел (НОК) — это наименьшее число, которое делится на оба данных числа.
Наибольший общий делитель двух чисел (НОД) — это наибольшее число, на которое делятся два данных числа.
последняя цифра числа четная;
сумма цифр числа делится на 3;
число заканчивается на 0 или на 5;
сумма цифр числа делится на 9;
последняя цифра числа равна 0;
суммы цифр на четных и нечетных позициях числа равны или их разность кратна 11.
Делитель и делимое числа. Делимость суммы и разности числа
Основной смысл процесса деления
На основе того, что мы озвучили, можно придать определенный смысл делению одного натурального числа на другое (отдельно выделим число, которое делят, и то, на которое делят). Мы помним, что понятие натуральных чисел проще всего соотнести с количеством некоторых предметов. То число, которое необходимо поделить, выражает число предметов исходного множества. В зависимости от того, какой смысл мы придаем второму числу (т.е. тому, на которое делят), можно выделить два основных подхода к пониманию смысла деления. Возможны такие варианты:
1. Исходное число, на которое осуществляется деление, соотносится с количеством предметов в тех множествах, что мы получили в результате деления. Тогда полученное после деления число будет означать количество получившихся множеств. Например, мы разделили 10 конфет на кучки по 2 штуки в каждой. Поделив 10 на 2, мы узнаем число кучек. 2. Исходное число, на которое мы делим, соответствует количеству получившихся множеств. Тогда результат деления будет показывать нам, сколько элементов входит в каждое такое множество. Вернувшись к примеру выше, мы увидим, что если 10 конфет разложить на 5 кучек, то число 2, получившееся в итоге, соответствует количеству конфет в каждой кучке.
Разделить одно натуральное число на другое без остатка возможно далеко не всегда. Так, 10 конфет мы можем ровно разделить на 2 или 5 кучек, а на 3 нет, потому что в одном из множеств окажется отличное от других число конфет. Разложить 10 конфет по 15 или 20 кучкам мы также не в состоянии. Смысл таких действий объясняется в материале про деление с остатком.
Если мы можем поделить одно натуральное число на другое, то получившееся в итоге число также будет натуральным.
Видео
Чем отличаются друг от друга, как найти
Делитель отличается от кратного тем, что:
Чтобы найти делители числа, нужно данное число разложить на множители.
Разложить на множители — представить число в виде произведения целых чисел.
Чтобы проверить, является ли одно число делителем другого, нужно разделить число на данное нам.
Для нахождения кратного числа заданному числу, нужно это число последовательно умножать на натуральные числа. Каждое полученное число будет кратно — будет делиться — заданному.
Делители и кратные связаны между собой. Например, делителем числа 15 является 3 и число, кратное 3, равно 15.
Деление многозначного числа на многозначное
При делении многозначного числа на многозначное поступаем точно так же, как поступали при делении многозначного числа на однозначное.
Разделяя число 37207 на 47, мы прежде всего определяем, из скольких цифр состоит частное. Частное меньше 1000 и больше 100, ибо 37207 меньше 47000 (47 × 1000) и больше 4700 (47 × 100), следовательно, частное состоит из сотен, десятков и единиц. Начиная с сотен, мы определяем каждую цифру частного отдельно:
Определяем сотни частного:
Делимое 37207 имеет 372 сотни. Десятки и единицы делимого не имеют влияния на цифру сотен частного. В частном может быть только 7 сотен, ибо 47 содержится в 372 семь раз; пишем в частном 700.
Умножая делитель на частное и вычитая из делимого, получаем первый остаток 4307.
Определяем десятки частного:
Остаток 4307 содержит 430 десятков. Единицы не имеют влияния на цифру десятков частного. Делитель 47 содержится в 430 девять раз; пишем в частном 90.
Умножая 90 на частное 47 и вычитая произведение 4330, получаем в остатке 77.
Определяем единицы частного:
47 содержится в 77 один раз. Пишем в частном 1 и, вычитая из 77 произведение единицы на делитель, получаем в остатке 30.
Итак, после деления имеем в целом частном 791 и в остатке 30.
Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, ход вычисления изобразится письменно:
Отделяем в делимом от левой руки к правой столько цифр, чтобы делитель мог содержаться в отделенной части делимого. В данном случае отделяем 3 цифры, 47 содержится в 372 семь раз; умножаем делитель 47 на 7, цифру частного, и, вычитая произведение 47 × 7 = 329 из 372, получаем в остатке 43.
К остатку 43 сносим 0, следующую цифру делимого; 47 содержится в 430 девять раз, пишем в частном 9. Умножая 47 на 9 и вычитая произведение 423 из 430, получаем остаток 7.
Сносим к остатку следующую цифру частного 7; 47 содержится в 77 один раз. Пишем единицу в частном.
Умножая ею делитель и вычитая 47 из 77, получаем в остатке 30 и в целом частно 791.
Пример. Разделить 671064 на 335. Деление изобразится письменно:
Отделяем 671 в делимом; 335 содержится в 671 два раза, пишем в частном 2. Умножая 335 на 2 и вычитая произведение 670, получим в остатке 1.
Сносим 0, следующую цифру делимого; 335 не содержится в 10, — пишем для второй цифры частного 0.
Сносим 6, следующую цифру делимого; 335 не содержится в 106, — пишем для третьей цифры частного 0.
Сносим следующую цифру делимого 4; 335 содержится в 1064 три раза, — пишем в частном 3. Умножая делитель на 3 и вычитая произведение, получим в остатке 59 и в целом частном 2003.
Из предложенных примеров выводим следующее правило:
Чтобы разделить многозначное число на однозначное или многозначное, нужно отделить в делимом от левой руки к правой столько цифр, сколько их находится в делителе. Если делитель не содержится, отделяют в делимом одной цифрой больше. Разделив отделенное число на делитель, получают первую цифру частного, умножают ей делитель и полученное произведение вычитают из отделенной части делимого.
К остатку сносят следующую цифру делимого и снова задаются.
Если при этом получается число меньше делителя, пишут в частном нуль, сносят следующую цифру и снова задаются.
Получив новую цифру частного, поступают с нею так же, как и с первой цифрой.
Деление продолжают до тех пор, пока не снесут всех цифр делимого и не получат таким образом всех цифр частного.
Всякий раз, когда приходится делить, нужно задаваться в частном такою цифрой, чтобы остаток был меньше делителя. Чтобы легче найти такую цифру частного, при делении многозначного числа на многозначное обращают внимание на одну или две старшие цифры делителя и задаются только ими в соответствующей части делимого. При этом в делимом и в делителе отделяют от правой руки к левой одинаковое число цифр. Так, определяя, сколько раз содержится 6373 в 27302, мы задаемся четырьмя, ибо 6 в 27 содержится 4 раза.
Полученная при этом цифра частного будет или равна или больше действительной. В последнем случае ее нужно уменьшить.
Иногда при делении не подписывают произведение цифры частного на делитель, а, подразумевая его в уме, подписывают один остаток. Сокращая таким образом деление, изображают его письменно:
8 в 43 содержится 5 раз; 5-ю 8 — сорок. Вычитая 40 из 43, получаем в остатке 3.
Сносим 2; 8 в 32 содержится 4 раза; 4-жды 8 составляет 32. Вычитая 32, получим в остатке нуль.
Сносим 8; 8 в 8-ми содержится 1 раз, 1-жды 8 составляет 8. Вычитая 8, получаем в остатке нуль и в частном 541.
Задачи, которые решаются при помощи действия деления
В курсе математики средней школы наиболее часто используется деление при решении таких задач, когда нужно:
Правило деления целых чисел
Частное двух целых чисел равно частному их модулей, со знаком плюс в результате, если числа одинаковых знаков, и со знаком минус, если они разных знаков.
Важно учитывать знак частного целых чисел. Кратко правила деления целых чисел:
Плюс на плюс дает плюс. “+ : + = +”
Минус на минус дает плюс. “– : – =+”
Минус на плюс дает минус. “– : + = –”
Плюс на минус дает минус. “+ : – = –”
А теперь рассмотрим подробно каждый пункт правила деления целых чисел.
Различные случаи при делении
При делении целых чисел бывают два случая:
Разделяя 12 на 4, мы находим в частном 3. Делитель 4 содержится ровно 3 раза в делимом 12. Вычитая последовательно из 12 по 4, мы могли вычесть число 4 ровно три раза и не получили никакого остатка. В этом случае говорят, что деление совершилось нацело или без остатка. Умножив частное 3 на делитель 4, получаем делимое 12.
Разделяя 26 на 8, мы при последовательном вычитании получаем:
26 — 8 = 18 18 — 8 = 10 10 — 8 = 2
Далее нельзя продолжать вычитания, потому что из 2 нельзя вычесть делитель 8. Число 2 называют остатком.
Остаток всегда меньше делителя. В этом случае говорят, что деление не совершается нацело или деление совершается с остатком.
Разделяя 26 на 8, мы могли вычесть делитель 8 три раза, и у нас получился остаток 2. Число 3 мы будем называть целым частным. Целое частное есть не полное частное, ибо оно не выражает вполне, сколько раз меньшее число содержится в большем. Число 8 не содержится в 26 ровно 3 раза. В этом случае говорят: число 8 содержится в 26 три раза и еще получается остаток. Умножив делитель 8 на целое частное 3, мы не получим делимого 26, а число 24 — меньшее делимого. Чтобы получить делимое, нужно к этому произведению прибавить еще остаток 2.
Целое частное иногда называют просто частным.
Итак, при делении мы имеем два случая:
Деление нацело или без остатка. Когда делитель содержится в делимом ровное число раз, тогда деление совершается нацело или без остатка. Частное выражает, сколько раз делитель содержится в делимом. Делимое равно делителю, умноженному на частное. В этом случае деление есть действие в котором по данному произведению и одному из производителей находится другой производитель.
Если дается произведение и множимое, отыскивают множитель, то есть число равных слагаемых; если дается произведение и множитель, отыскивают множимое, то есть величину равных слагаемых.
Деление с остатком. Когда делитель не содержится в делимом ровное число раз, тогда деление не совершается нацело, или деление совершается с остатком. Остаток всегда меньше делителя и делимое равно произведению делителя на целое частное, сложенное с остатком.
При делении целых чисел делимое всегда уменьшается во столько раз, сколько в делителе единиц, поэтому деление есть действие, обратное умножению.
Проверка частного деления целых чисел
Как говорилось ранее деление и умножение тесно связаны. Поэтому чтобы проверить результат деления двух целых чисел, нужно выполнить умножение делителя и частного в результате должно получиться делимое.
Проверка результата деления краткая формула: Делитель ∙ Частное = Делимое
Рассмотрим пример: Выполните деление и сделайте проверку 1888:(-32).
Решение: Обращаем внимание на знаки целых чисел. Число 1888 положительное и имеет знак “+”. Число (-32) отрицательное и имеет знак “–”. Поэтому при делении двух целых чисел с разными знаками ответ будет отрицательное число. 1888:(-32)=-59
Вопросы по теме: Что такое частное чисел? Ответ: частное чисел – это результат деления деления двух чисел.
Как найти частное? Ответ: нужно одно число поделить на другое, то есть делимое поделить на делитель и получим частное.
Чему равно частное от деления целых чисел? Ответ: если целые числа делятся без остатка, то их частное равно целому числу. Иначе будет дробное число.
Что такое делимое и делитель? Ответ: число которое делят называют делимым, а число на которое делят называют делителем.
Пример: Найдите частное суммы и разности чисел 48 и 16.
Решение: Находим сумму чисел 48 и 16. 48+16=64 Находим разность чисел 48 и 16. 48-16=32 Находим частное. 64:32=2 Ответ: 2.
Деление
Деление чисел довольно непростая операция как в освоении, так и в использовании. Рекомендуем набраться терпения, чтобы осилить этот урок до конца.
Что такое деление?
Деление это действие, позволяющее что-либо разделить.
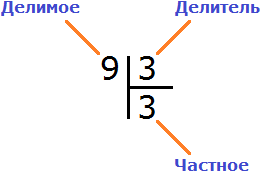
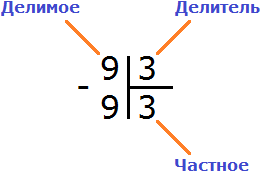
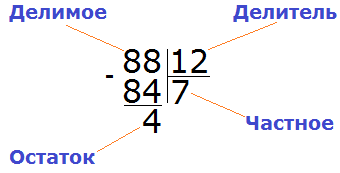
Деление состоит из трёх параметров: делимого, делителя и частного.
Делимое это то что делят;
Делитель это число, показывающее на сколько частей нужно разделить делимое.
Частное это собственно результат.
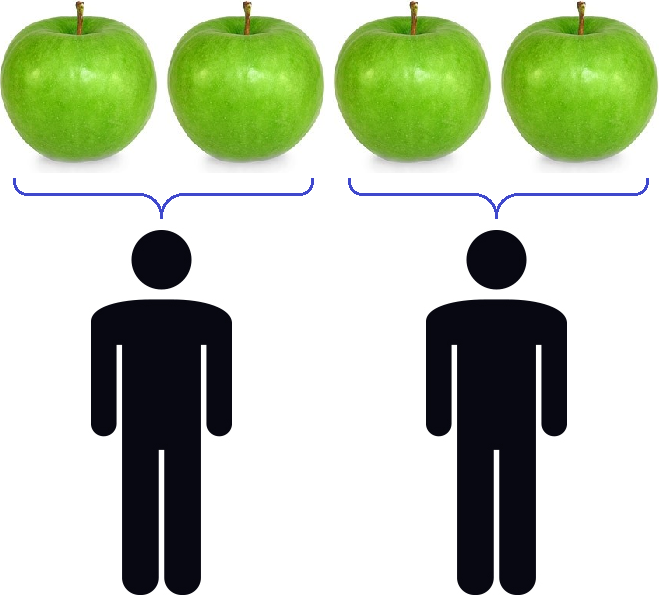
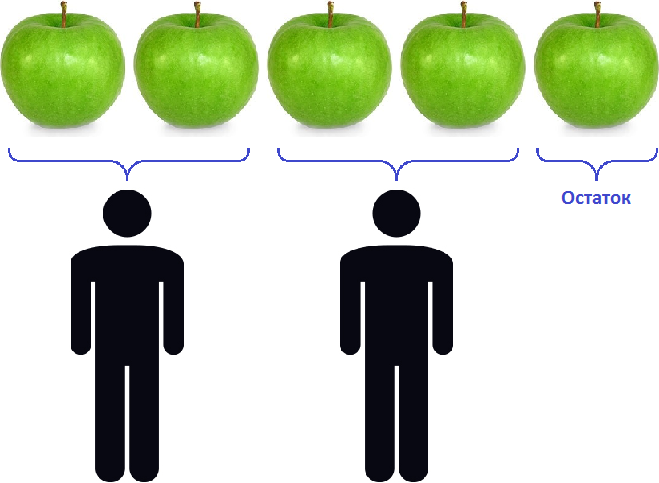
Пусть у нас имеются 4 яблока:
Разделим их поровну на двоих друзей. Тогда деление покажет сколько яблок достанется каждому. Нетрудно увидеть, что каждому достанется по два яблока:
Процесс деления четырех яблок на двоих друзей можно описáть следующим выражением:
В этом примере роль делимого играют яблоки. Роль делителя играют двое друзей, показывающих на сколько частей нужно разделить 4 яблока. Роль частного играют два яблока, показывающие сколько досталось каждому.
Знак деления выглядит в виде двоеточия : но также можно встретить знак двоеточия и тире ÷
На письме разумнее использовать двоеточие, поскольку оно выглядит аккуратнее.
Деление с остатком
Остаток — это то, что осталось от действия деления неразделённым.
Например, пять разделить на два будет два и один в остатке:
5 : 2 = 2 (1 в остатке)
Можно проверить это умножением:
Допустим, у нас имеются пять яблок
Разделим их поровну на двоих друзей. Но разделить поровну пять целых яблок не получится. Тогда данное деление покажет, что каждому достанется два яблока, а одно яблоко будет в остатке:
Деление уголком
Когда требуется разделить большое число, то прибегают к такому методу как деление уголком.
Прежде чем делить уголком, человек должен понимать:
Это простой пример. Все знают, что девять разделить на три будет три. Ответ (частное) записывается под правым углом:
Пример 2. Найти значение выражения 8 : 3
Восемь на три просто-так не разделится. Таблица умножения тоже не поможет. В данном случае будет присутствовать остаток от деления.
Сначала запишем данное выражение уголком:
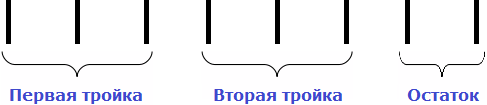
Теперь надо задать вопрос: «сколько троек в восьмёрке?» В восьмёрке содержится две тройки. Это можно увидеть даже воочию, если мы представим восьмёрку как восемь палочек:
Теперь вынимаем остаток. Для этого умножаем частное на делитель (2 на 3) и записываем полученное число под делимым:
Далее из 8 вычитаем 6. Полученное число и будет остатком:
8 : 3 = 2 (2 в остатке)
Проверка: (2 × 3) + 2 = 6 + 2 = 8
Деление многозначного числа на однозначное
Данная тема с первого раза может показаться непонятной. Не спешите отчаиваться и забрасывать обучение. Понимание придёт в любом случае. Если не сразу, то немного позже. Главное не сдаваться и продолжать упорно изучать.
В предыдущих примерах мы делили однозначное число на однозначное, и это не доставляло нам лишних проблем. Сейчас мы займёмся тем, что будем делить многозначное число на однозначное.
Если непонятно, что такое однозначные и многозначные числа, советуем изучить предыдущий урок, который называется умножение.
Чтобы разделить многозначное число на однозначное, нужно сначала посмотреть на первую цифру этого многозначного числа, и проверить больше ли она делителя. Если больше, то разделить, а если нет, то проверить больше ли делителя первые две цифры многозначного числа. Если первые две цифры больше делителя, то разделить, а если нет, то проверить больше ли первые три цифры многозначного числа. И так до тех пор, пока не будет выполнено первое деление.
Сложно? Ни чуть, если мы разберём несколько примеров.
Пример 1. Найти значение выражения 25 : 3
25 это многозначное число, а 3 — однозначное. Применяем правило. Смóтрим на первую цифру многозначного числа. Первая цифра это 2. Два больше, чем три? Нет. Поэтому смóтрим первые две цифры многозначного числа. Первые две цифры образуют число 25. Двадцать пять больше, чем три? Да. Поэтому выполняем деление числа 25 на 3. Записываем уголком данное выражение и начинаем делить:
Сколько троек в числе 25? Если с первого раза ответить сложно, можно заглянуть в таблицу умножения на три. Там необходимо отыскать произведение, которое меньше 25, но очень близко к нему или равно ему. Если найдём такое произведение, то необходимо забрать оттуда множитель, который дал такое произведение:
Это таблица умножения на три. В ней необходимо найти произведение, которое меньше 25, но очень близко к нему или равно ему. Очевидно, что это произведение 24, которое выделено синим. Из этого выражения необходимо забрать множитель, который дал такое произведение. Это множитель 8, который закрашен красным.
Данная восьмёрка и отвечает на вопрос сколько троек в числе 25. Записываем её в правом уголке нашего примера:
Теперь вынимаем остаток. Для этого умножаем частное на делитель (8 на 3) и полученное число записываем под делимым:
Теперь из делимого вычитаем число 24, получим 1. Это и будет остатком:
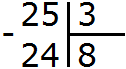
25 : 3 = 8 (1 в остатке)
(8 × 3) + 1 = 24 + 1 = 25
Последний остаток всегда меньше делителя. Если последний остаток больше делителя это означает, что деление не завершено.
В приведённом примере последним остатком было число 1, а делителем число 3. Единица меньше, чем три, поэтому деление завершено. Последний остаток, меньший делителя, говорит о том, что он не содержит чисел, равных делителю.
Пример 2. Разделить 326 на 4.
Смотрим на первую цифру числа 326. Первая цифра это 3. Она больше делителя 4? Нет. Тогда проверяем две цифры делимого. Две цифры делимого образуют число 32. Больше ли оно делителя 4? Да, больше. Поэтому делим. Записываем уголком данное выражение:
Данная восьмёрка, которая выделена красным отвечает на вопрос сколько четвёрок в числе 32. Записываем её в правом уголке нашего примера:
Теперь умножаем 8 на 4, получаем 32 и записываем это число под делимым. Далее вычитаем это число из 32. Получим 0. Поскольку решение ещё не завершено, ноль не записываем:
Первое число 32 разделили. Осталось разделить оставшуюся 6. Для этого сносим эту шестёрку:
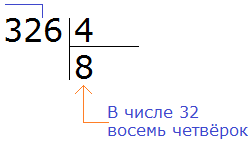
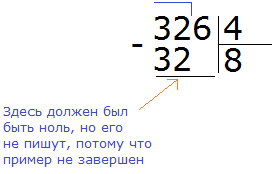
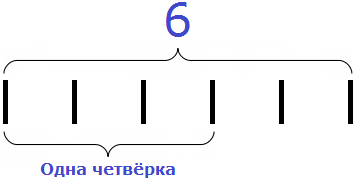
Теперь делим 6 на 4. Для этого задаём вопрос: «сколько четвёрок в шестёрке?» В шестёрке одна четвёрка, это можно увидеть воочию, если представить шестёрку как шесть палочек:
Записываем единицу в правом уголке нашего ответа:
Теперь умножаем нашу единицу на делитель (1 на 4) и записываем полученное число под шестёркой:
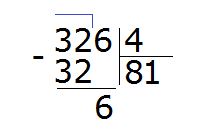
Затем из 6 вычитаем 4, получаем число 2, которое является остатком:
Получили 326 : 4 = 81 (2 в остатке)
Проверка: (81 × 4) + 2 = 324 + 2 = 326
Процедура, в которой мы ищем первое число для деления, сравнивая больше ли оно делителя или меньше, называется нахождением первого неполного делимого.
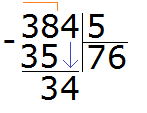
Пример 3. Найти значение выражения 384 : 5
Записываем данное выражение в уголком:
Сначала находим первое неполное делимое. Первая цифра меньше делителя, поэтому проверяем две цифры. Две цифры вместе образуют число 38, которое больше делителя. Это число будет первым неполным делимым. Его и будем в первую очередь делить на делитель:
Сколько пятёрок в числе 38? Если сразу ответить сложно, то можно посмотреть в таблицу умножения на пять и найти произведение, которое меньше 38, но очень близко к нему или равно ему. Найдя такое произведение, нужно забрать оттуда множитель, который будет отвечать на наш вопрос:
Это таблица умножения на пять. Находим произведение, которое меньше 38, но очень близко к нему или равно ему. Очевидно, что это произведение 35, которое выделено синим. Из этого выражения забираем множитель, который дал такое произведение. Это множитель 7, который выделен красным.
Данная семёрка отвечает на вопрос сколько пятёрок в числе 38. Записываем эту семёрку в правом уголке нашего примера:
Умножаем 7 на 5, получаем 35 и записываем его под 38:
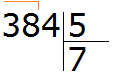
Теперь из 38 вычитаем 35, получим 3:
Эта тройка является остатком, которая осталась неразделённой в результате деления 38 на 5. Но видно, что ещё надо разделить и 4. Эту 4 мы снесём и разделим вместе с тройкой:
Видно, что в таблице умножения на пять число 30 меньше нашего 34, но близко к нему. Из этого выражения забираем множитель 6, который отвечает на наш вопрос. Записываем эту шестёрку в правом уголке нашего примера:
Теперь умножаем 6 на 5, получаем 30 и записываем это число под 34:
Теперь из 34 вычитаем 30, получаем 4. Эта четвёрка будет остатком от деления 384 на 5
384 : 5 = 76 (и 4 в остатке)
Проверка: (76 × 5) + 4 = 380 + 4 = 384
Пример 4. Найти значение выражения 8642 : 4
Этот пример немного посложнее. Записываем уголком данное выражение:
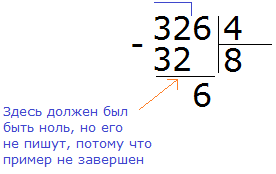
Первая цифра 8 больше делителя. Эта восьмёрка будет первым неполным делимым. Делим 8 на 4, получаем 2
Теперь умножаем 2 на 4, получаем 8. Записываем эту восьмёрку под первым неполным делимым:
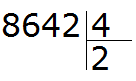
Далее сносим цифру 6 и делим её на делитель, получаем 1
Умножаем 1 на 4, получаем 4. Записываем эту четвёрку под снесённой шестёркой. Затем вынимаем остаток, отняв от шести четыре:
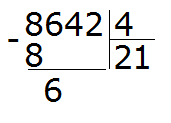
Получили остаток 2. Это остаток, который остался от деления 6 на 4.
Теперь сносим следующую цифру из делимого. Это цифра 4. Эта четвёрка вместе с предыдущим остатком 2 образует число 24. Его делим на делитель. Получим 6
Умножаем 6 на 4, получаем 24. Записываем это число под 24
Поэтому два разделить на четыре это ноль:
Умножаем 0 на 4, получаем 0. Пишем этот 0 под двойкой:
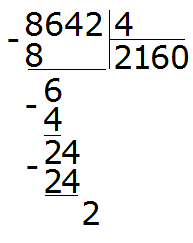
8642 : 4 = 2160 (2 в остатке)
Проверка: (2160 × 4) + 2 = 8640 + 2 = 8642
Деление чисел, у которых на конце 0
Чтобы разделить число, у которого на конце ноль, нужно временно отбросить этот ноль, выполнить обычное деление, и дописать этот ноль в ответе.
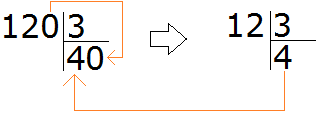
Например, разделим 120 : 3
Сколько троек в числе 120? Чтобы ответить на этот вопрос, временно отбрасываем ноль на конце у 120 и делим 12 на 3, получаем 4. И дописываем этот ноль в частном. В итоге получаем 40:
Проверка 40 × 3 = 120.
Такие простые примеры не нуждаются в том, чтобы их решали уголком. Достаточно знать таблицу умножения. Далее просто дописывать нули на конце. Например:
12 : 3 = 4 (делимое без нулей на конце)
120 : 3 = 40 (здесь у делимого один ноль)
1200 : 3 = 400 (здесь у делимого два нуля)
12000 : 3 = 4000 (здесь у делимого три нуля)
В этом способе есть небольшой подвох. Если вы заметили, деля такие числа, мы ссылаемся на таблицу умножения. А представьте, что надо разделить 400 на 5.
Можно рассуждать по старому — отбросить временно все нули и разделить обычные числа. А что будет если отбросить все нули в числе 400? Мы обнаружим, что делим 4 на 5, что недопустимо. В этом случае, надо отбрасывать только один ноль, и делить 40 на 5, а не 4 на 5
Завершаем этот пример, как обычно умножая частное на делитель, и выводя остаток:
Этот способ работает только в том случае, если удаётся гладко применить таблицу умножения. В остальных случаях, придётся искать обходные пути, вычисляя уголком или собирая частное подобно детскому конструктору.
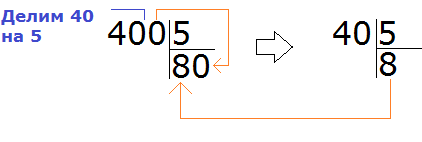
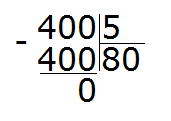
Например, найдём значение выражения 1400 : 5. Здесь отбрасывание нулей нам ничего не даст. Этот пример надо решать уголком или собрать ответ, подобно конструктору. Давайте рассмотрим второй способ.
Что такое 1400? Вспоминаем разряды чисел. 1400 это одна тысяча и четыре сотни:
Можно по-отдельности разделить 1000 на 5 и 400 на 5:
1000 : 5 = 200
400 : 5 = 80
и сложить полученные результаты:
200 + 80 = 280
Итого: 1400 : 5 = 280
Решим этот же пример уголком:
Деление многозначного числа на многозначное
Здесь придётся хорошенько напрячь свой мозговой аппарат и выжать из него по максимуму, потому что разделить многозначное число на многозначное не так то просто.
Принцип деления остаётся тем же что и раньше. Здесь так же надо находить первое неполное делимое. Здесь так же могут присутствовать остатки от деления.
Для начала введём новое понятие — круглое число. Круглым будем называть число, которое оканчивается нулём. Например, следующие числа являются круглыми:
10, 20, 30, 500, 600, 1000, 13000
Любое число можно превратить в круглое. Для этого первые цифры, образующие старший разряд, оставляют без изменений, а остальные цифры заменяют нулями.
Например, превратим число 19 в круглое число. Первая цифра этого числа 1 образует старший разряд (разряд десятков) — эту цифру оставляем как есть, а оставшуюся 9 заменяем на ноль. В итоге получаем 10
Ещё пример. Превратим число 125 в круглое число. Первая цифра 1 образует старший разряд (разряд сотен) — эту цифру оставляем без изменений, а оставшиеся цифры 25 заменяем нулями. В итоге получаем 100.
Ещё пример. Превратим число 2431 в круглое число. Первая цифра 2 образует старший разряд (разряд тысяч) — эту цифру оставляем без изменений, а остальные цифры 431 заменяем нулями. В итоге получаем 2000.
Ещё пример. Превратим число 13 735 в круглое число. Первые две цифры 13 образуют старший разряд (разряд десятков тысяч) — эти две цифры оставляем без изменений, а остальные цифры 735 заменяем нулями. В итоге получаем 13 000.
Возвращаемся к делению многозначных чисел на многозначные. Сложность деления таких чисел заключается в том, что частное надо находить методом подбора. Для этого прибегают к различным техникам, например, превращают делимое и делитель в круглые числа.
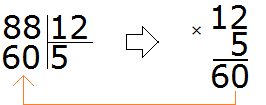
Пример 1. Найти значение выражения 88 : 12
Записываем данное выражение уголком:
Задаём вопрос сколько чисел 12 в числе 88? С первого раза ответить сложно. Придётся рассуждать.
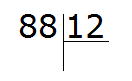
Давайте попробуем угадать частное. К сожалению, его просто так с неба взять нельзя. Это частное должно быть таким, чтобы при его умножении на делитель, получалось число, которое меньше делимого, но очень близко к нему или равно ему.
Давайте предположим, что частное равно 2. Умножаем это частное на делитель 12
Что это нам дало? Полученное число меньше делимого, но близко к нему? Нет. Оно конечно же меньше делимого 88, но очень далеко от него. Значит двойка как частное не подходит.
Пробуем следующее число. Допустим частное равно 5
Полученное число конечно меньше, но оно не близко к делимому 88. Значит пятёрка как частное тоже не подходит.
Попробуем сразу взять по 8
На этот раз полученное число превзошло делимое. А оно должно быть меньше делимого, но очень близким к нему или равным ему. Значит восьмёрка как частное тоже не подходит Попробуем тогда взять по 7
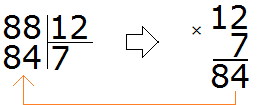
Наконец-то нашли подходящее частное! Умножив частное 7 на делитель 12, мы получили 84, которое меньше делимого, но близко к нему. Теперь находим остаток от деления. Для этого из 88 вычитаем 84, получаем 4.
88 : 12 = 7 (4 в остатке)
Проверка: (12 × 7) + 4 = 84 + 4 = 88
Как видно из примера, на подбор частного уходит драгоценное время. Если мы будем сидеть на контрольной или на экзамене, где каждая минута очень дорогá, этот метод нам явно не поможет.
Чтобы сэкономить время, можно делимое и делитель превратить в круглые числа, а затем осуществить деление этих круглых чисел. Делить круглые числа намного проще и удобнее.
Например, чтобы разделить 90 на 10, достаточно отбросить нули у обоих чисел и разделить 9 на 1. В итоге получим 90 : 10 = 9.
Количество отбрасываемых нулей должно быть строго одинаковым. К примеру, если мы делим 900 на 90, то отбрасываем по нулю от каждого числа, поскольку у числа 900 два нуля, а у 90 только один. Отбросив по нулю от каждого числа, мы получим выражение 90 : 9 = 10. В итоге получаем 900 : 90 = 10.
В делении круглых чисел также нет ничего сложного. Постарайтесь понять это. Если непонятно, изучите этот момент несколько раз. Это очень важно.
Ниже приведено несколько примеров, где делятся круглые числа. Отбрасываемые нули закрашены серым цветом:
80 0 : 1 0 = 80 (отбросили по нулю и разделили 80 на 1, получили 80)
80 0 : 8 0 = 10 (отбросили по нулю и разделил 80 на 8, получили 10)
90 0 : 1 0 = 90 (отбросили по нулю и разделили 90 на 1, получили 90)
40 0 : 5 0 = 8 (отбросили по нулю и разделили 40 на 5, получили 8)
32 0 : 8 0 = 4 (отбросили по нулю и разделили 32 на 8, получили 4)
Заметно, что всё в конечном итоге свóдится к таблице умножения. Именно поэтому в школе требуют знать её наизусть. Мы тоже этого требуем, хоть и не принуждаем.
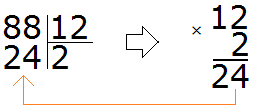
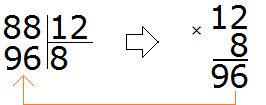
Теперь давайте решим предыдущий пример 88 : 12 где мы бились, находя частное методом угадывания.
Для начала превращаем делимое и делитель в круглые числа.
Круглым числом для 88 будет число 80.
А круглым числом для 12 будет число 10.
Теперь делим полученные круглые числа:
80 разделить 10 будет 8. Эту восьмёрку мы пишем в частном:
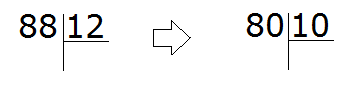
Теперь проверяем, верно ли подобралось частное. Для этого умножаем частное на делитель (8 на 12). Восьмёрку как частное мы уже проверяли, когда решали этот пример методом угадывания. Она нам не подошла, поскольку после её умножения на делитель, получилось число 96, которое больше делимого. Зато подошло частное 7, которое меньше восьмёрки всего-лишь на единицу.
Отсюда можно сделать вывод, что в выражении 88 : 12 частное, полученное путём превращения делимого и делителя в круглые числа, больше лишь на единицу. Наша с вами задача уменьшить это частное на единицу.
Так и сделаем — уменьшим 8 на единицу: 8 − 1 = 7. Семёрка это частное. Записываем её в правом уголке нашего примера:
Как видно, этим способом мы решили этот пример намного быстрее.
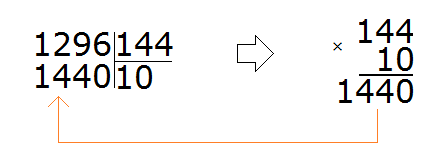
Пример 2. Найти значение выражения 1296 : 144
Записываем уголком данное выражение. Сразу же находим первое неполное делимое. Его образуют все четыре цифры делимого:
Это деление многозначного числа на многозначное. Давайте применим только что изученный метод. Превратим делимое и делитель в круглые числа, а затем разделим их.
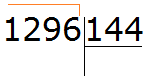
Для делимого 1296 круглым числом будет 1000. А для делителя 144 круглым числом будет 100.
Делим 1000 на 100, получим 10. Проверим полученную десятку, умножив её на делитель 144
Десятка не подходит, поскольку при умножении получается число, которое больше делимого.
Попробуем взять по 9, уменьшив десятку на единицу.
Проверяем девятку. Для этого умножаем её на делитель:
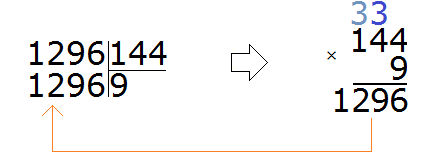
Красота! Полученное число оказалось не только ближе к делимому, но и равным ему. Это значит, что деление выполнилось без остатка. Завершаем данный пример, вычитая из 1296 полученное число 1296
1296 : 144 = 9
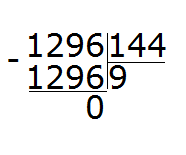
Проверка: 144 × 9 = 1296
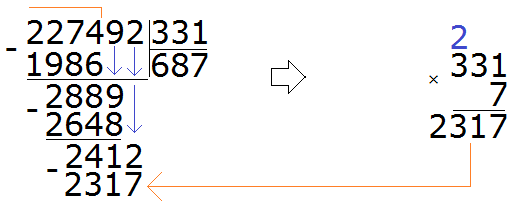
Пример 3. Попробуем решить большой и сложный пример 227 492 : 331
Записываем уголком данное выражение. Сразу же определяем первое неполное делимое. Его образуют первые четыре цифры делимого 2274. Значит сначала будем делить 2274 на 331. Их же превратим в круглые числа.
Для числа 2274 круглым числом будет 2000. А для 331 круглым числом будет 300
Получили 6. Проверим верно ли подобралась эта шестёрка. Для этого, умножим её на делитель 331:
Шестёрка подошла, потому что она отвечает на вопрос сколько чисел 331 в числе 2274. Если бы мы взяли по семь, то получилось бы следующее:
Если бы мы взяли по 7 и проверили эту семёрку, то получили бы 2317, которое больше делимого, а это недопустимо.
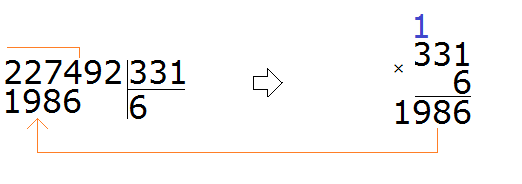
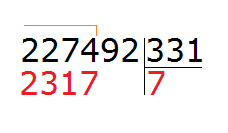
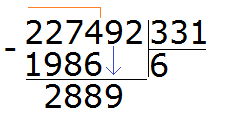
Продолжаем решать наш пример. Вычитаем из 2274 число 1986, получаем 288:
288 это остаток от деления 2274 на 331. Далее, чтобы продолжить деление, нужно снести девятку:
Теперь надо разделить 2889 на 331. Превращаем их в круглые числа и делим их. Сразу же проверяем полученное таким способом частное:
Умножив 6 на 331, мы снова получили 1986. Это число должно быть меньше делимого 2889, но близким к нему или равным ему. Но 1986 очень далеко от него. Значит шестёрка, как частное не подходит. Проверим тогда семёрку. Это первый случай, когда нам не помог второй способ, который экономил нам время. Дальнейшее решение придётся проводить методом угадывания частного:
Проверили семёрку. Снова получили число, которое далеко от делимого 2889. Значит семёрка тоже не подходит. Проверим восьмёрку:
Восьмёрка подошла. Она отвечает на вопрос сколько чисел 331 в числе 2889. Если бы мы взяли по девять, то при умножении на делитель, получили бы число 2979, а это уже больше делимого 2889.
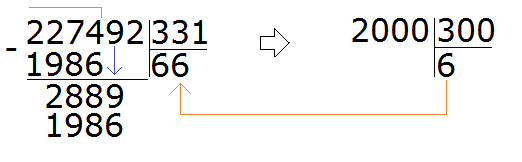
Теперь вынимаем остаток от деления 2889 на 331. Для этого от 2889 вычитаем 2648 и получаем 241
241 это остаток от деления 2889 на 331. Чтобы продолжить деление, нужно снести 2 из главного делимого:
Теперь делим 2412 на 331. Возьмём по 7
Теперь находим последний остаток. Для этого из 2412 вычитаем 2317, получаем 95. На этом пример завершается:
227 492 : 331 = 687 (95 в остатке)
Проверка: (331 × 687) + 95= 227 397 + 95 = 227 492
На этом данный урок можно завершить. Не расстраивайтесь, если сразу не научитесь делить числа уголком. Этот навык нарабатывается со временем в сочетании с интенсивными тренировками. Ошибки дело не страшное. Самое главное — понимать.
Отметим, что в данном уроке рассмотрено только деление с остатком. Деление без остатка мы рассмотрим в следующих уроках. Сделано это с целью не усложнять обучение. Как говорится, всему своё время.