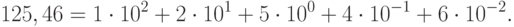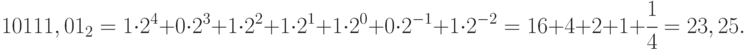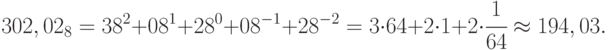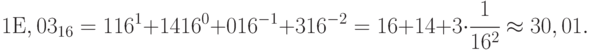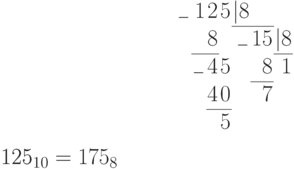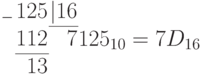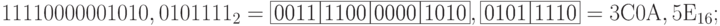Десятичный эквивалент что это

Перевод чисел из одной системы счисления в другую

Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.

Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.

Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
200₁₀ = 11001000₂ = 310₈ = C8₁₆

Кратко об основных системах счисления

Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.

Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.

Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.

Перевод в десятичную систему счисления

Перевод из десятичной системы счисления в другие

Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.

Переведем число 375₁₀ в восьмеричную систему:

Перевод из двоичной системы в восьмеричную

Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:

Перевод из двоичной системы в шестнадцатеричную

Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:

Тетрада	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
Цифра	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

Перевод из восьмеричной системы в двоичную

Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.

Используем таблицу триад:

Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.

Перевод из шестнадцатеричной системы в двоичную

Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.

Используем таблицу тетрад:

Цифра	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Тетрада	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111

Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.

Перевод из восьмеричной системы в шестнадцатеричную и наоборот

Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.

Источник

Как записать десятичный эквивалент числа

Вычислите десятичные эквиваленты следующих двоичных чи-
сел:
111₂
1010₂
11011₂
101101₂

так надо написать на 5

Здравствуйте! На рисунке изображён график функции у =f(х). Точки a, b, с, d и е задают на оси х четыре интервала. Помогите пользуясь ( Подробнее. )

2. В чем заключается принцип Ферма?

Плата за телефон составляет 350 рублей в месяц. В следующем году она увеличится на 12%. Сколько рублей придётся платить ежемесячно за ( Подробнее. )

Приведите примеры информации, которая в конкретной ситуа-
ции является:
актуальной (своевременной)/неактуальной ( Подробнее. )

От разведчика была получена шифрованная радиограмма, пере-
данная с использованием азбуки Морзе. При передаче радио-
граммы ( Подробнее. )

Ответ оставил Гуру

Если тебя не устраивает ответ или его нет, то попробуй воспользоваться поиском на сайте и найти похожие ответы по предмету Информатика.

Помогите записать десятичные эквиваленты чисел, не понимаю как это сделать.172 (8) (восьмёрка в учебнике записана маленьким шрифтом внизу) 2EA(16) 101010(2) 10,1(2) 243(6)

Лучший ответ:

Цифры записанные внизу указывают систему счисления
172₈ – число записано в восьмеричной системе счисления. Требуется перевести его в десятичной системе счисления.
172₈ = 1*8² 7*8¹ 2*8⁰ = 64 56 2 = 122₁₀ – т.е. 122 в десятичной
2ЕА₁₆ = 2*16² 14*16¹ 10*16⁰ = 512 224 10 = 746₁₀
101010₂ = 1*2⁵ 0*2⁴ 1*2³ 0*2² 1*2¹ 0*2⁰ = 32 0 8 0 2 0 = 42₁₀
10,1₂ = 1*2¹ 0*2⁰ 1*2⁻¹ = 2 0 1/2 = 2,5₁₀
243₆ = 2*6² 4*6¹ 3*6⁰ = 72 24 3 = 99₁₀

Источник

ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА

Двоично-десятичная система счисления. Десятичные цифры от 0 до 9 заменяются представляющими их двоичными тетрадами: 0=0000, 1=0001, 2=0010, 3=0011, 4=0100, 5=0101, 6=0110, 7=0111, 8=1000 и 9=1001. Такая запись очень часто используется как промежуточный этап перевода числа из десятичной системы в двоичную или обратно. Так как 10 не является точной степенью 2, то используются не все 16 тетрад, а алгоритмы арифметических операций над многозначными числами здесь более сложны, чем в основных системах счисления. И тем не менее, двоично-десятичная система счисления применяется даже на этом уровне во многих микрокалькуляторах и некоторых компьютерах (в частности, «Ямаха» стандарта MSX).

Принцип построения этой системы достаточно прост: каждая десятичная цифра преобразуется прямо в свой десятичный эквивалент из 4 бит, например: 369110=0011 0110 1001 0001DEC:

Десятичное число 3 6 9 1 Двоично-десятичное число 0011 0110 1001 0001

Преобразуем двоично-десятичное число 1000 0000 0111 0010 в его десятичный эквивалент. Каждая группа из 4 бит преобразуется в её десятичный эквивалент. Получим 1000 0000 0111 0010DEC = 807210:

Двоично-десятичное число 1000 0000 0111 0010 Десятичное число 8 0 7 2

Микропроцессоры используют чистые двоичные числа, однако понимают и команды преобразования в двоично-десятичную запись. Полученные двоично-десятичные числа легко представимы в десятичной записи, более понятной людям.

Преобразование двоичных чисел в двоично-десятичные

Арифметико-логическое устройство AVR-микроконтроллеров (как и других микропроцессоров) выполняет элементарные арифметические и логические операции над числами, представленными в двоичном коде. В двоичном коде считываются результаты преобразования АЦП, в двоичном коде (в формате целых чисел или чисел с плавающей точкой) удобно выполнять обработку результатов измерения. Однако, когда окончательный результат отображается на индикаторе, он должен быть преобразован в десятичный формат, удобный для восприятия человеком.

В данном разделе рассматриваются программы преобразования двоичных чисел в двоично-десятичные.

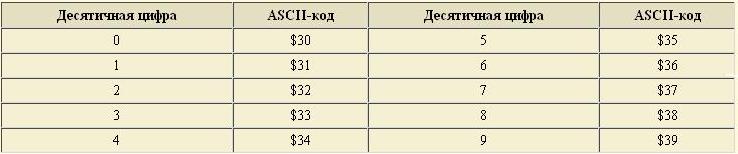
1. Форматы представления десятичных чисел

Неупакованный десятичный код является подмножеством международной таблицы кодирования символов ASCII (Таблица 1). Видно, что для хранения неупакованных десятичных чисел требуется в два раза больше памяти, так как каждая цифра представляется 8-битным кодом. Таблица 1: ASCII-коды десятичных цифр

2. Преобразование целых 16-битных чисел в двоично-десятичные числа

На сайте www.atmel.com предлагается программа «bin2bcd16» для преобразования целых 16-битных двоичных чисел в двоично-десятичные упакованные числа. В данной статье рассматривается программа «bin16bcd5» (см. Приложение, Программа 1), написанная Терешкиным А. В. согласно алгоритму, изложенному в [1], и выполняющая ту же задачу. Последняя программа по быстродействию, длине кода и количеству используемых регистров оказалась более эффективной, чем первая.

Алгоритм программы «bin16bcd5» заключается в следующем. Предположим, что имеется целое беззнаковое 16-битное число (диапазон от 0 до 65535). Очевидно, что необходимо найти 5 десятичных цифр. Способ преобразования заключается в том, чтобы, вычитая из исходного числа число 10000, сначала определить десятичную цифру десятков тысяч. Затем находится цифра тысяч последовательным вычитанием числа 1000 и т. д. Вычитание каждый раз производится до получения отрицательной разности с подсчетом числа вычитаний. При переходе к определению каждого следующего десятичного разряда в регистрах исходного числа восстанавливается последняя положительная разность. После того, как будет найдена десятичная цифра десятков, в регистрах исходного числа останется десятичная цифра единиц.

Программа «bin16ASCII5» (см. Приложение, Программа 2) преобразует целое двоичное 16-битное число в десятичное неупакованное число. При этом используется тот же алгоритм.

3. Преобразование двоичной дроби в двоично-десятичную дробь

Двоичная дробь, по определению, представляется следующим выражением:

Из этого представления следует алгоритм преобразования (Рис. 2), который содержит m шагов. На каждом шаге к двоично-десятичному результату прибавляется очередная двоичная цифра и весь результат делится на 2.

На изображены двоичный регистр, который содержит исходную двоичную дробь и регистр двоично-десятичного упакованного результата. Для наглядности у обоих регистров также показаны разряд единиц и положение точки, которые в памяти микропроцессора никак не представлены, но положение которых всегда строго оговорено. Количество циклов рассматриваемого алгоритма равно количеству бит двоичной дроби. Разрядность двоично-десятичного регистра определяется требуемой точностью вычислений.

Сложить эту цифру с двоично-десятичным числом означает, что ее нужно поместить в разряд единиц двоично-десятичного числа, откуда при последующем делении на два цифра A-i сдвинется в старший разряд старшей тетрады десятичной дроби. При программировании мы можем представлять, что разрядом единиц десятичной дроби является бит переноса С.

При делении на два двоично-десятичного упакованного числа, так же как и при делении двоичного числа, его сдвигают вправо на один разряд. При этом на два делится каждая тетрада, то есть каждая десятичная цифра. При делении четной десятичной цифры в соответствующем разряде снова получается десятичная цифра, и никакой коррекции не требуется. При делении на 2 нечетной десятичной цифры остаток, равный 5, должен быть добавлен к более младшему десятичному разряду, но на самом деле при двоичном сдвиге в более младшую тетраду добавляется число 8 (вес старшего разряда тетрады). Поэтому требуется коррекция результата, которая заключается в вычитании числа 3 из содержимого тех тетрад, которые после сдвига вправо имеют установленные старшие разряды.

4. Преобразование чисел с плавающей точкой в двоично-десятичные числа

Представление чисел с плавающей точкой имеет следующий вид:

Такое представление часто используется и в десятичной системе счисления для представления очень больших или очень малых чисел. Мантисса и порядок представляют собой целые знаковые числа. Знак мантиссы является знаком всего числа. Порядок показывает истинное положение точки вместо того, которое она занимает в изображении мантиссы. Двоичное число с плавающей точкой отличается от привычного нам десятичного тем, что точка является двоичной, то есть порядок показывает на количество двоичных (а не десятичных) разрядов, на которое необходимо переместить эту точку влево или вправо.

Нормализованным представлением числа с плавающей точкой называют такое представление, когда мантисса является правильной дробью, и старшая ее цифра отличается от нуля. Но для двоичного числа требование того, что старшая цифра отличается от нуля означает, что эта цифра равна 1. Если старшая цифра точно известна, то ее можно не хранить в памяти.

Источник

Десятичное число 1439 =

== двоично-десятичному числу 1010000111001 (3 нуля в начале опущены) Написание:

Написание числа 1439 в двоично-десятичной системе

5.3. Вычисление десятичного эквалента двоичного числа 10110011111

Вычисленный десятичный эквивалент

Буквы. Шестая и седьмая дорожки совместно с дорожками, предназначенными для кодирования цифр, используются для кодирования букв и специальных знаков. Рис. 5.7 показывает, что существует определенная система кодирования букв (английского) алфавита, хотя код ASCII несколько отличается от кода EIA244A. В коде ASCII алфавит кодируется пробиванием отверстий в шестой и седьмой дорожках с добавлением чисто двоичного кода номера буквы от 1 до 26 на дорожках с первой по пятую, поскольку в алфавите 26 букв. Код EIA244A следует двоично-десятичное системе счисления за счет разделения алфавита на три группы по десять букв. Группы кодируются следующим образом.

Буквы алфавита от А до I: отверстия в шестой и седьмой дорожках; буквы от J до R: отверстия в седьмой дорожке; буквы от S до Z: отверстия в шестой дорожке. Внутри группы цифры нумеруются с 1 до 9 в двоичной системе.

Внимательный читатель уже вероятно заметил некоторое несоответствие в описании процедуры кодирования букв в коде EIA244A. Ведь алфавит состоит из 26 букв, а не из 27, поэтому «три группы по девять букв» оставляют одну комбинацию неиспользованной. Сможете ли вы определить по рис. 5.7, какая комбинация пропущена и какому месту в алфавите это соответствует?

Проверка четности. Пятая дорожка в коде EIA244A и восьмая дорожка в коде ASCII зарезервированы для проверки надежности перфоратора и устройства считывания программы, установленного на станке. По установленному жесткому правилу число отверстий в каждом горизонтальном ряду всегда должно быть четным (в случае кода EIA244A) или нечетным (в случае кода ASCII). Это правило называется проверкой четности (или нечетности в зависимости от кода). Поскольку некоторым знакам двоично-десятичного кода соответствует четное количество отверстий, а некоторым — нечетное, дорожка четности используется для добавления в случае необходимости отверстия, обеспечивающего четность (или нечетность) каждого горизонтального ряда. Цель этой операции сейчас будет объяснена.

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Двоичные числа и двоичная арифметика

Принцип представления чисел в позиционных системах счисления

Позиционной называется система счисления, в которой вес разряда числа определяется его позицией в записи числа [1].

сотни десятки единицы десятые доли сотые доли

Аналогично любое число в десятичной системе счисления можно представить в виде подобной суммы:

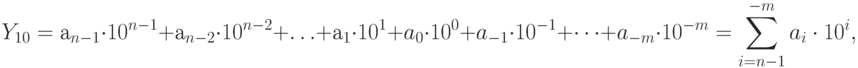( 11.1)

Для числа в системе счисления с основанием выражение (11.1) преобразуется к виду:

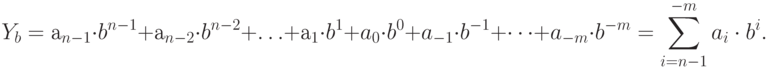( 11.2)

Таблица 11.1. Параметры позиционных систем счисления

Название системы счисления	Основание системы счисления	Знаки, использующиеся для записи чисел
Двоичная	2	0, 1
Троичная	3	0, 1, 2
Четверичная	4	0, 1, 2, 3
…	…	…
Восьмеричная	8	0, 1, 2, 3, 4, 5, 6, 7
…	…	…
Десятичная	10	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
…	…	…
Шестнадцатеричная	16	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
…	…	…

Приведем примеры записи чисел в указанных системах и найдем их десятичные эквиваленты по формуле (11.2).

Для двоичного числа:

Для восьмеричного числа:

Для шестнадцатеричного числа:

Округление относится к дробной части числа, целая часть переводится точно. Особенностью перевода из шестнадцатеричного кода в десятичный код является то, что в качестве коэффициента используется десятичный эквивалент шестнадцатеричного знака в соответствии с таблицей 11.2. Для нашего примера вместо знака » » в расчетную формулу (11.2) подставляется десятичное число .

Из рассмотренных примеров видно, что общая формула (11.2) может использоваться для перевода числа из системы счисления с любым основанием в десятичную.

Перевод чисел из одной системы счисления в другую

Перевод из десятичной системы в любую другую. Перевод целых чисел

Проверка перевода осуществляется по формуле (11.2), так, как это показано ниже на примерах.

Пример. Перевести десятичное число 125 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Проверить результаты по формуле (П11.2).

В рассмотренном примере при переводе вместо коэффициента используется его десятичный эквивалент в соответствии с таблицей 11.2.

Перевод из двоичной системы в шестнадцатеричную (восьмеричную)

Как уже было сказано выше, шестнадцатеричный и восьмеричный коды используются для более компактной и удобной записи двоичных чисел. Так, программирование в машинных кодах осуществляется в большинстве случаев в шестнадцатеричном коде. Правила перевода для шестнадцатеричной и восьмеричной системы структурно одинаковы, отличия для восьмеричной системы отображаются в скобках.

Двоичная запись числа делится на группы по четыре ( три ) двоичных знака влево и вправо от запятой, отделяющей целые и дробные части Неполные крайние группы (если они есть) дополняются нулями до четырех ( трех ) знаков. Каждая группа заменяется одним шестнадцатеричным ( восьмеричным ) знаком в соответствии с кодом группы (табл. 11.2).

Таблица 11.2. Соответствие двоичных групп, шестнадцатеричных и восьмеричных знаков

Двоичная группа	Шестнадцатеричный знак	Десятичный эквивалент	Двоичная группа	Восьмеричный знак
0000	0	0	000	0
0001	1	1	001	1
0010	2	2	010	2
0011	3	3	011	3
0100	4	4	100	4
0101	5	5	101	5
0110	6	6	110	6
0111	7	7	111	7
1000	8	8
1001	9	9
1010	A	10
1011	B	11
1100	C	12
1101	D	13
1110	E	14
1111	F	15

Перевод из шестнадцатеричной (восьмеричной) системы в двоичную

Каждая цифра (без всяких сокращений!) шестнадцатеричного ( восьмеричного ) числа заменяется одной двоичной группой из четырех ( трех ) двоичных знаков (табл. 11.2).

Как показано в примерах, крайние нули слева и справа при желании можно не писать, но такое сокращение делается уже после перевода в двоичную систему.

Источник