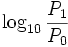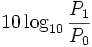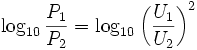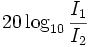Децибелы это что такое простыми словами
Что такое децибел
Очень часто новички сталкивается с таким понятием, как децибел. Многие из них интуитивно догадываются, что это такое, но у большинства до сих пор возникают вопросы.
Что такое децибел?
Относительные логарифмические единицы Белы (децибелы) широко используются при количественных оценках параметров различных аудио, видео, измерительных устройств. Физическая природа сравниваемых мощностей может быть любой — электрической, электромагнитной, акустической, механической, — важно лишь, чтобы обе величины были выражены в одинаковых единицах — ваттах, милливаттах и т. п. Бел выражает отношение двух значений энергетической величины десятичным логарифмом этого отношения, причем под энергетическими величинами понимаются: мощность, энергия.
Кстати, эта единица получила свое название в честь Александра Белл (1847 — 1922) — американского ученого шотландского происхождения, основоположника телефонии, основателя всемирно известных компаний AT&T и «Bell Laboratories». Еще интересно напомнить, что во многих современных мобильных телефонах (смартфонах) обязательно есть выбираемый звук звонка (оповещения), так и называемый «bell». Впрочем, Бел относится к единицам, не входящим в Международную систему единиц (СИ), но в соответствии с решением Международного комитета мер и весов допускается к применению без ограничений совместно с единицами СИ. В основном применяется в электросвязи, акустике, радиотехнике.
Формулы для вычисления децибелов
P1 — мощность до усиления, Вт
P2 — мощность после усиления или ослабления, Вт
На практике, оказалось, что удобнее пользоваться уменьшенным в 10 раз значением Бел, т.е. децибел, поэтому:
дециБел (дБ) = 10 * lg(P2/P1)
Усиление или ослабление мощности в децибелах выражается формулой:
NдБ — усиление, либо ослабление мощности в децибелах
P1 — мощность до усиления, Вт
P2 — мощность после усиления или ослабления, Вт
Значения Бел, децибел могут быть со знаком «плюс», если P2 > P1 (усиление сигнала) и со знаком «минус», если P2
Во многих случаях, сравнение сигналов путем измерения мощностей может быть неудобным или невозможным — проще измерить напряжение или ток.
В этом случае, если мы сравниваем напряжения или токи, формула примет уже другой вид:
NдБ — усиление, либо ослабление мощности в децибелах
U1 — это напряжение до усиления, В
U2 — напряжение после усиления, В
I2 — сила тока после усиления, А
Вот небольшая табличка, в которой приведены основные отношения напряжений и соответствующее число децибел:
Дело в том, что операции умножения и деления над числами в обычном базисе, заменяются операциями сложения и вычитания в логарифмическом базисе. Например, у нас есть два каскадно-включенных усилителя с коэффициентами усиления K1 = 963 и K2 = 48. Какой общий коэффициент усиления? Правильно — он равен произведению K = K1 * K2. Вы можете в уме быстро вычислить 963*48? Я — нет. Я могу прикинуть K = 1000*50 = 50 тыс., не более. А, если нам известно, что K1 = 59 дБ и K2 = 33 дБ, то К = 59+33 = 92 дБ — сложить было не трудно, надеюсь.
Закон Вебера-Фехнера
Почему именно децибелы? Все исходит от закона Вебера-Фехнера, который говорит нам, что интенсивность ощущения человеческих чувств прямо-пропорциональна логарифму интенсивности какого-либо раздражителя.
Так светильник, в котором восемь лампочек, кажется нам настолько же ярче светильника из четырёх лампочек, насколько светильник из четырёх лампочек ярче светильника из двух лампочек. То есть количество лампочек должно увеличиваться каждый раз вдвое, чтобы нам казалось, что прирост яркости постоянен. То есть если добавить к нашим 32 лампочкам на графике еще одну лампочку, то мы даже и не заметим разницы. Для того, чтобы для нашего глаза была заметна разница, мы должны к 32 лампочкам добавить еще 32 лампочки, и т.д. Или иными словами, для того, чтобы нам казалось, что наш светильник плавно набирает яркость, нам надо зажигать вдвое больше лампочек каждый раз, чем было предыдущее значение.
Поэтому децибел действительно удобнее в некоторых случаях, так как сравнивать две величины намного проще в маленьких цифрах, чем в миллионах и миллиардах. А так как электроника — это чисто физическое явление, то и децибелы не обошли ее стороной.
Децибелы и АЧХ усилителя
Как вы помните в прошлом примере с ОУ, у нас неинвертирующий усилитель усиливал сигнал в 10 раз. Если посмотреть в нашу табличку, то это получается 20 дБ относительно входного сигнала. Ну да, так оно и есть:
Также в дБ на некоторых графиках АЧХ обозначают наклон характеристики АЧХ. Это может выглядеть примерно вот так:
Давайте рассмотрим пример. Имеем фильтр высоких частот (ФВЧ) первого порядка, собранного на RC-цепи.
Его АЧХ будет выглядеть следующим образом (кликните для полного открытия)
Итак возьмем первую точку на частоте в 10 Герц. На частоте в 10 Герц амплитуда сигнала уменьшилась на 44 дБ, это видно в правом нижнем углу (out:-44)
Умножаем частоту на 10 (декада) и получаем вторую точку в 100 Герц. На частоте в 100 Герц наш сигнал уменьшился приблизительно на 24 дБ
Что еще измеряют в децибелах?
Uc — это эффективное значение напряжения сигнала, В
Uш — эффективное значение напряжения шума, В
Чем выше значение сигнал/шум, тем более чистый звук обеспечивается аудиосистемой. Для музыкальной аппаратуры желательно, чтобы это отношение было не менее 75 дБ, а для Hi-Fi аппаратуры не менее 90 дБ. Не имеет значение физическая природа сигнала, важно, чтобы единицы были в одинаковых измерениях.
В качестве единицы логарифмического отношения двух одноимённых физических величин применяется также непер (Нп) — 1 Нп
0,8686 Б. В основе лежит не десятичный (lg), а натуральный (ln) логарифм отношений. В настоящее время используется редко.
Во многих случаях, удобно сравнивать между собой не произвольные величины, а одну величину относительно другой, названной условно опорной (нулевой, базовой).
В электротехнике, в качестве такой опорной или нулевой величины выбрано значение мощности равное 1 мВт выделяемое на резисторе сопротивлением 600 Ом.
В этом случае, базовыми значениями при сравнении напряжений или токов станут величины 0.775 В или 1.29 мА.
Для звуковой мощности такой базовой величиной является 20 микроПаскаль (0 дБ), а порог +130 дБ считается болевым для человека:
Более подробно об этом написано в Википедии по этой ссылке.
Для случаев когда в качестве базовых значений используются те или иные конкретные величины, придуманы даже специальные обозначения единиц измерений:
dbW (дБВт) — здесь отсчет идет относительно 1 Ватта (Вт). Например, пусть уровень мощности составил +20 дБВт. Это значит что мощность увеличилась в 100 раз, то есть на 100 Вт.
dBm (дБм) — здесь у нас отсчет уже идет относительно 1 милливатта (мВт). Например, уровень мощности в +30дБм будет соответственно равен 1 Вт. Не забываем, что это у нас энергетические децибелы, поэтому для них будет справедлива формула
Следующие характеристики — это уже амплитудные децибелы. Для них будет справедлива формула
dBV (дБВ) — как вы догадались, опорное напряжение 1 Вольт. Например, +20дБВ даст — это 10 Вольт
От дБВ также вытекают другие виды децибелов с разными приставками:
dBmV (дБмВ) — опорный уровень 1 милливольт.
dBuV (дБмкВ) — опорное напряжение 1 микровольт.
Здесь я привел наиболее употребимые специальные виды децибелов в электронике.
Децибелы используются и в других отраслях, где они также показывают отношение каких-либо двух измеряемых величин в логарифмическом масштабе.
Также на YouTube есть интересное видео о децибелах.
Децибелл
Децибе́л — десятая часть бела, безразмерной единицы для измерения отношения некоторых величин (например, энергетических — мощности и энергии или силовых — напряжения и силы тока) по логарифмической шкале. Другими словами, децибел — это некая относительная величина. Не абсолютная физическая, как например, грамм или метр, а такая же относительная, как кратность или проценты, предназначенная для измерения отношения («разности уровней») других величин, обычно сигналов. Сегодня децибел в основном применяется в акустике (где в децибелах измеряется громкость звука) и электронике.
Децибел не является официальной единицей в системе единиц СИ, хотя, по решению Генеральной конференции по мерам и весам, допускается его применение без ограничений совместно с СИ, а Международная палата мер и весов рекомендовала включить его в эту систему.
Содержание
Области применения
Первоначально децибел использовался для измерения отношений энергетических (мощность, энергия) или силовых (напряжение, сила тока) величин. В принципе, с помощью децибелов можно измерять что угодно, но в настоящее время рекомендуется употреблять децибелы только для измерения уровня мощности и некоторых других связанных с мощностью величин. Так децибелы сегодня используются в акустике для измерения громкости звука и в электронике для измерения мощности электрического сигнала. Иногда в децибелах также измеряют динамический диапазон (например, звучания музыкальных инструментов). Также децибел является единицей звукового давления.
Измерение мощности
Как уже было сказано выше, изначально белы использовались для оценки отношения мощностей, поэтому в каноническом, привычном смысле величина, выраженная в белах, означает логарифмическое отношение двух мощностей и вычисляется по формуле:
величина в белах =
где P1 / P0 — отношение уровней двух мощностей, обычно измеряемой к т. н. опорной, базовой (взятой за нулевой уровень). Если говорить более точно, то это — «белы по мощности». Тогда отношение двух величин в «децибелах по мощности» вычисляется по формуле:
величина в децибелах (по мощности) =
Измерение немощностных величин
Формулы для вычисления в децибелах разностей уровней немощностных (неэнергетических) величин, таких как напряжение или сила тока, отличаются от приведённой выше! Но в конечном итоге отношение этих величин, выраженное в децибелах, также выражается через отношение связанных с ними мощностей.
Так для линейной цепи справедливо равенство 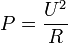
Отсюда видим, что 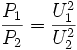
откуда получаем равенство: 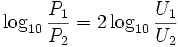
Из всего этого видим, что при сравнении величин напряжений (U1 и U2) или токов (I1 и I2) их отношения в децибелах выражаются формулами:
децибелы по напряжению = 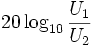
Можно подсчитать, что при измерении мощности изменению на 1 дБ соответствует приращение мощности (P2/P1) в ≈1,25893 раза. Для напряжения или силы тока изменению на 1 дБ будет соответствовать приращение в ≈1,122 раза.
Пример вычислений
Предположим, что мощность P2 в 2 раза больше начальной мощности P1, тогда
то есть изменение мощности на 3 дБ означает её увеличение в 2 раза. Аналогично изменение мощности в 10 раз:
И, наоборот, чтобы получить разы из децибел (dB), нужно
Например, зная опорный уровень (P1) и значение в дБ можно найти значение мощности, например, при P1 = 1 мВт и известном отношении 20 дБ (dB):
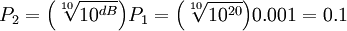
Аналогично для напряжения, при U1 = 2 В и отношении в 6 дБ :
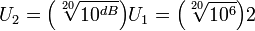
Вычисления вполне реально производить в уме, для этого достаточно помнить примерную несложную таблицу (для мощностей):
1 дБ 1.25 3 дБ 2 6 дБ 4 9 дБ 8 10 дБ 10 20 дБ 100 30 дБ 1000
Сложению (вычитанию) значений дБ соответствует умножение (деление) самих отношений. Отрицательные значения дБ соответствуют обратным отношениям. Например, уменьшение мощности в 40 раз это 4*10 раз или −6 дБ-10 дБ= −16 дБ. Увеличение мощности в 128 раз это 2^7 или 3 дБ*7=21 дБ. Увеличение напряжения в 4 раза эквивалентно увеличению мощности в 4*4=16 раз, это 2^4 или 3 дБ*4=12 дБ.
Практическое применение
Поскольку децибел — не абсолютная, а относительная величина и вычисляется для различных физических величин по-разному (см. выше), то во избежание путаницы при использовании децибелов на практике существуют дополнительные договорённости.
чаще всего нужно знать отношение двух уровней (напряжений), выраженное в децибелах, есть несколько значений, которые легко запомнить:
6 дБ — отношение 2:1
20 дБ — отношение 10:1
40 дБ — отношение 100:1
60 дБ — отношение 1000:1
80 дБ — отношение 10000:1
100 дБ — отношение 100000:1
120 дБ — отношение 1000000:1
Промежуточные значения можно легко вычислить по формуле — 20*Lg(U1/U2), где U1 — уровень(напряжение) сигнала,U2 — уровень(напряжение) шума, напомним, что измерения проводятся средне-квадратичным милливольтметром, либо анализатором спектра с фильтром МЭК(А), где МЭК — Международная электротехническая комиссия
Зачем вообще применять децибелы и оперировать логарифмами, если то же самое можно выразить привычными процентами или долями? Представим себе, что в совершенно тёмной комнате включили лампочку некоторой светосилы. При этом, комната разительно отличается по виду до и после включения. Изменение освещённости, выраженное в дБ, тоже огромно, теоретически бесконечно. Допустим, что теперь включили ещё одну такую же лампочку. Теперь эффект будет совсем не тот, может быть даже человек не сразу заметит изменения, если её включить плавно. И в децибелах это будет всего 3 дБ. Итак, на практике, в децибелах удобно выполнять измерения как сильно меняющихся величин, так и почти постоянных.
Условные обозначения
Для различных физических величин одному и тому же числовому значению, выраженному в децибелах, могут соответствовать разные уровни сигналов (вернее разности уровней). Поэтому во избежание путаницы такие «конкретизированные» единицы измерения обозначают теми же буквами «дБ», но с добавлением индекса — общепринятого обозначения измеряемой физической величины. Например «дБВ» (децибел относительно вольта) или «дБмкВ» (децибел относительно микровольта), «дБВт» (децибел относительно ватта) и т. п. В соответствии с международным стандартом МЭК 27-3 при необходимости указать исходную величину ее значение помещают в скобках за обозначением логарифмической величины, например для уровня звукового давления: LP (re 20 µPA) = 20 dB; LP (исх. 20 мкПа) = 20 дБ
Применение в теории автоматического регулирования
Децибел также используется в теории автоматического регулирования и управления (ТАУ) и является одним из важнейших параметров при сравнении амплитуд выходного и входного сигналов.
Опорный уровень
Несмотря на то, что децибел служит для определения отношения двух величин, иногда децибелы используют и для измерения абсолютных значений. Для этого достаточно условиться, какой уровень измеряемой физической величины будет принят за опорный уровень (условный 0). На практике распространены следующие опорные уровни и специальные обозначения для них:
Во избежание путаницы желательно указывать опорный уровень явно, например −20 дБ (относительно 0,775 B).
При пересчёте уровней мощностей в уровни напряжений и обратно надо обязательно учитывать сопротивление, являющиеся стандартным для данной задачи:
Следует чётко помнить математические правила:
Например, подав на один конец 50-омного кабеля с коэффициентом передачи −6 дБ, мощность 0 дБм, что эквивалентно 1 мВт, или 0,22 В, или 107 дБмкВ, на выходе получим мощность −6 дБм, что эквивалентно 0,25 мВт (в 4 раза меньше по мощности) или 0,11 В (в два раза меньше по напряжению) или 101 дБмкВ (на те же 6 дБ меньше).
Что такое децибел?
Изображённый на фотографии прибор называется измерителем уровня громкости звука, а по-простому — шумомером. Нажмём на кнопку и посмотрим, что он покажет. Оказывается, в тихой комнате, где я сейчас нахожусь, уровень звука составляет 35 дБ (читается «35 децибел»). То есть какой-то звук здесь всё-таки есть, хотя я и сижу молча и неподвижно. И в самом деле, если прислушаться, то можно услышать, как хлопнула дверь в подъезде, проехала машина на улице, где-то вдали идёт поезд — прибор реагирует на все эти звуки и отображает на дисплее общий уровень шума. А что будет, если я заговорю? Уровень звука теперь прыгает между 55 и 70 дБ. Было 35 — стало 70. Означает ли это, что звук стал в два раза громче? Похоже, что нет — ведь было совсем тихо, а стало довольно громко — и с этим надо разобраться.
Для начала давайте поймём, что такое громкость звука и как её можно измерять. Всякий звук — это волна, которая распространяется в упругой среде, например, в воздухе. Волны создаются колеблющимися телами и распространяются от них во все стороны, перенося механическую энергию. Именно эта энергия заставляет колебаться барабанную перепонку нашего уха или мембрану микрофона. Наш шумомер — это прежде всего микрофон; чем больше энергия, переносимая волной, тем больше амплитуда колебаний мембраны микрофона и тем больше электрический ток, который течёт от этого микрофона по проводам. Мы измеряем этот ток и по его величине узнаём, какова была энергия звуковой волны, которая заставила колебаться мембрану.
Если энергия — слишком абстрактное понятие для вас, подойдём к делу по-другому. Пусть в комнате вместо одного человека с той же самой громкостью разговаривают десять человек одновременно. Естественно считать, что при этом шум в комнате станет в десять раз громче. А физик скажет, что десять одновременно говорящих людей по сравнению с одним человеком создают в десять раз большую звуковую энергию.
Однако при чём здесь децибелы? Ведь это какая-то совсем другая единица? Это правильный вопрос, и с ним полезно будет разобраться. Тем более что это не только интересная физика, но и хорошая математика.
Мы начнём с того, что дадим определение децибела, и его надо внимательно прочитать. Говорят, что один сигнал сильнее («громче») другого на 10 децибел, когда энергия первого сигнала превышает энергию второго сигнала в 10 раз. Прочитайте это определение ещё раз, чтобы привыкнуть, потому что на первый взгляд оно звучит достаточно странно. А теперь давайте с ним разбираться.
Самое главное в этом определении то, что оно связывает две разные арифметические операции — сложение и умножение. «Больше на» — это сложение; «больше в» — умножение. Найдём, во сколько раз будет различаться энергия двух сигналов, когда один из них будет громче другого на 30 дБ. Первый сигнал будет громче второго на 10 дБ, плюс ещё на 10 дБ, плюс ещё на 10 дБ. Применяем определение и понимаем, что энергия первого сигнала будет больше энергии второго сигнала в 10 раз, потом ещё в 10 раз, и потом ещё в 10 раз. Но увеличить что-то в 10 раз три раза подряд — значит увеличить его в 10 × 10 × 10 = 1000 раз.
Но что же такое тогда звук в 0 дБ, от которого идёт отсчёт шкалы громкости? Это вовсе не отсутствие звука в физическом смысле — это такой уровень звука, когда человеческое ухо перестаёт что-либо слышать. Звук в физическом смысле, как колебания воздуха, ещё есть, но мы его уже не слышим, потому что он для нас слишком слабый. Если этот звук сделать в 10 раз громче, его уровень станет равным 10 дБ, увеличение громкости ещё в 10 раз даст уровень 20 дБ, и так далее. Заметьте также, что громкость звука на шкале децибел может быть отрицательной — просто такие звуки мы не будем слышать, хотя какое-нибудь более чуткое ухо или физический прибор всё равно сможет их фиксировать.
Если уровень звука на громкой дискотеке равен 100 дБ, это означает, что он в 10 000 000 000 раз (десять нулей) громче самого тихого звука, который мы можем слышать. Примерные значения разных уровней громкости показаны в этой таблице. Интересно заметить, что психологически мы воспринимаем скорее децибелы, чем звуковую энергию: громкий и тихий разговор различаются на 30 дБ, но никто не почувствует, что разговор стал в 1000 раз громче.
| 15 | Шелест листвы |
| 20 | Тихий шёпот, 1 м |
| 35 | Тиканье настенных часов |
| 45 | Тихий разговор |
| 60 | Спокойный разговор |
| 75 | Громкий разговор |
| 80 | Шум пылесоса |
| 90 | Тяжёлый грузовик, 7 м |
| 100 | Концерт рок-музыки |
| 110 | Вертолёт |
| 120 | Отбойный молоток |
| 140 | Взлёт реактивного самолета, 25 м |
| 150 | Взлёт ракеты, 100 м |
| 160 | Выстрел из ружья вблизи уха |
Задачи
1. Сколько нужно собрать человек, чтобы они, разговаривая одновременно, издавали звук такой же громкости, как один вертолёт?
2. По определению, если один звук громче другого на 10 дБ, то он громче этого второго звука в 10 раз. А если два звука различаются на 5 дБ, во сколько раз один из них будет громче другого?
1. По таблице в статье вертолёт громче спокойного разговора на 50 дБ. Значит, громкость вертолёта равна громкости разговора 10 5 = 100 000 человек.