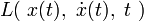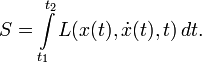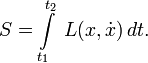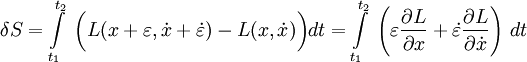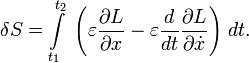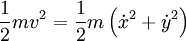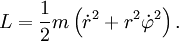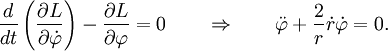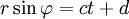Действие в физике что такое
ДЕЙСТВИЕ (в физике)
Смотреть что такое «ДЕЙСТВИЕ (в физике)» в других словарях:
Действие (физическая величина) — У этого термина существуют и другие значения, см. Действие (физика). Действие Размерность L2MT−1 Действие в физике скалярная физическая величина, являющаяс … Википедия
Действие (механика) — В физике принцип действия является утверждением о природе движения, из которого может быть определена траектория объекта, на который действуют внешние силы. Траектория объекта та, которая приводит к постоянному значению для физической величины,… … Википедия
Действие (физика) — У этого термина существуют и другие значения, см. Действие. Термин действие употребляется в физике в нескольких специальных значениях: как название фундаментальной физической величины, в значении, близком к разговорному: действие сил или… … Википедия
Действие — физическая величина, имеющая размерность энергии на время. В классической механике, да и во всей физике, применим т. н. «принцип наименьшего действия», который постулирует, что из всех возможных движений системы, при определенных установленных… … Начала современного естествознания
Важнейшие открытия в физике — История технологий По периодам и регионам: Неолитическая революция Древние технологии Египта Наука и технологии древней Индии Наука и технологии древнего Китая Технологии Древней Греции Технологии Древнего Рима Технологии исламского мира… … Википедия
Эфир в физике — Содержание: 1) Э. до эпохи Декарта. 2) Э. картезианцев. 3) Э. Гюйгенса, Ньютона и позднейшего времени. 4) Свойства Э., как вида материи, согласно современным воззрениям. 5) Плотность Э. 6) Э. и тяготение. 7) Э. и молекулы обычных тел. 8) Инерция… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Эфир, в физике — Содержание: 1) Э. до эпохи Декарта. 2) Э. картезианцев. 3) Э. Гюйгенса, Ньютона и позднейшего времени. 4) Свойства Э., как вида материи, согласно современным воззрениям. 5) Плотность Э. 6) Э. и тяготение. 7) Э. и молекулы обычных тел. 8) Инерция… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Список обозначений в физике — Необходимо проверить качество перевода и привести статью в соответствие со стилистическими правилами Википедии. Вы можете помочь … Википедия
Реакция (действие) — Реакция (лат. re… против + лат. actio действие) действие, возникающие в ответ на какое либо воздействие. Содержание 1 В химии и физике 2 В биологии и медицине 3 В э … Википедия
Действие (физическая величина)
Из Википедии — свободной энциклопедии
\mathrm Действие в физике — скалярная физическая величина, являющаяся мерой движения физической системы. Действие является математическим функционалом, который берёт в качестве аргумента траекторию движения физической системы и возвращает в качестве результата вещественное число. Действие — одна из фундаментальных физических величин, входящая в современную формулировку большинства основных физических теорий во всех фундаментальных разделах физики, имеющая при этом и огромное значение в теоретической физике. Оно может иметь меньшее значение в сравнительно более прикладных областях, хотя и там нередко бывает употребительно. Используется равно и в квантовой, и в классической, и в релятивистской физике. В классической механике принцип наименьшего действия постулирует, что физическая система всегда следует траектории с наименьшим действием. В квантовой механике, в формулировке теории через интегралы по траекториям, физическая система одновременно следует всем возможным траекториям, причём амплитуда вероятности следования определённой траектории определяется действием этой траектории. Если характерное действие намного больше постоянной Планка, то амплитуда классической траектории с наименьшим действием является преобладающей — таким образом квантовая механика переходит в классическую. Если для какой-то системы написано действие, то это в принципе определяет и её классическое поведение (то есть поведение системы в классическом приближении), и её квантовое поведение. Первое — через принцип стационарного (наименьшего) действия, второе — через фейнмановский интеграл по траекториям. При этом само действие записывается одинаково, в одной и той же форме, и для классического, и для квантового случая, что делает его очень удобным инструментом (для квантования через фейнмановский интеграл в принципе надо знать только действие, определённое для обычных классических траекторий, то есть записанное так же, как и для классического применения). В физике при́нцип де́йствия является утверждением о природе движения, из которого может быть определена траектория объекта, на который действуют внешние силы. Траектория объекта — та, которая приводит к постоянному значению для физической величины, названной действием. Таким образом, вместо того, чтобы думать об объекте, ускоряющемся в ответ на приложенные силы, можно было думать о силах, которые выделяют траектории со стационарным действием. Принцип также называют принципом стационарного действия и также принцип Гамильтона-Остроградского. Другая формулировка принципа как принцип наименьшего действия менее общая и фактически неправильная. Действие — скаляр (число) с единицей измерения «Действия» как «Энергия» умножить на «Время». Принцип — простое, общее и мощное средство для того, чтобы предсказать движение в классической механике. Расширения принципа действия описывают релятивистскую механику, квантовую механику, электричество и магнетизм. Хотя принцип эквивалентен законам Ньютона в классической механике, но принцип действия лучше подходит для обобщений и играет важную роль в современной физике. Действительно, этот принцип — одно из больших обобщений в физике. В частности, это полностью оценено и лучше всего понято в пределах квантовой механики. Формулировка квантовой механики Ричардом Фейнманом с помощью интегралов по траекториям основана на принципе стационарного действия в качестве классического (т.е. неквантового) предела (иными словами, принцип стационарного действия дает классический предел для фейнмановского интеграла по траекториям). Используя интегралы по траекториям, уравнения Максвелла могут быть получены как условия стационарного действия. Много проблем в физике могут быть представлены и решены в форме принципа действия, типа обнаружения самого быстрого пути спуска к берегу, чтобы достичь тонущего человека. Текущая вода ищет самый крутой спуск, самый быстрый путь вниз, и вода, сталкивающаяся с бассейном, распределяет себя так, чтобы его поверхность была настолько низка, насколько возможно. Свет находит самый быстрый путь через оптическую систему (принцип Ферма). Траектория тела в поле тяготения (то есть свободное падение в пространстве-времени, так называемая геодезическая) может быть найдена, используя принцип действия. Симметрии в физической ситуации можно лучше понять, используя принцип действия, вместе с уравнениями Эйлера-Лагранжа, которые получены из принципа действия. Например, теорема Нётер, которая гласит, что каждой непрерывной симметрии в физической ситуации соответствует закон сохранения (верно и обратное). Эта глубокая связь, однако, требует, чтобы принцип действия был принят. В классической механике правильный выбор действия может быть доказан из законов движения Ньютона. И наоборот, из принципа действия доказываются уравнения движения Ньютона, при правильном выборе действия. Так, в классической механике принцип действия является эквивалентным уравнениям движения Ньютона. Использование принципа действия часто проще, чем прямое решение уравнений движения Ньютона. Принцип действия — скалярная теория, с производными и применениями, которые используют элементарное исчисление. Принцип наименьшего действия был сначала сформулирован Мопертюи [1] в 1746 году и далее развивался (после 1748 года) математиками Эйлером, Лагранжем и Гамильтоном. Мопертюи пришёл к этому принципу из ощущения, что совершенство вселенной требует определенной экономии в природе и противоречит любым бесполезным расходам энергии. Естественное движение должно быть таким, чтобы сделать некоторую величину минимальной. Нужно было только найти эту величину, что он и продолжал делать. Она являлась произведением продолжительности (время) движения в пределах системы на удвоенную величину, которую мы теперь называем кинетической энергией системы. Эйлер (в «Reflexions sur quelques loix generales de la nature», 1748) принимает принцип наименьшего количества действия, называя его «усилием». Его выражение соответствует тому, что мы теперь назвали бы потенциальной энергией, так что его утверждение наименьшего количества действия в статике эквивалентно принципу, что система тел в покое примет конфигурацию, которая минимизирует полную потенциальную энергию. Уравнения движения Ньютона можно получить многими способами, т.е. Ньютонова механика может быть аксиоматически сформулирована по-разному. Один из них с помощью лагранжева формализма, также называемого лагранжевой механикой. Если обозначить траекторию движения частицы, как функцию времени t как x(t), со скоростью Действие S — интеграл от лагранжиана по времени между заданной начальной точкой x(t1) в момент времени t1 и заданной конечной точкой x(t2) в момент времени t2 Стационарная точка интеграла вдоль пути эквивалентна системе дифференциальных уравнений, названных уравнениями Эйлера-Лагранжа. Это может быть замечено следующим образом (ограничимся одномерным случаем). Обобщение на многомерный случай тривиально. Предположим, имеется интеграл действия S с подинтегральной функцией L, который зависит от координат x(t) и их производных dx(t)/dt, по времени t: Рассмотрим вторую кривую x1(t), которая начинается и заканчивается в тех же точках, что и первая кривая, и предположим, что расстояние между двумя кривыми мало: ε(t) = x1(t) — x(t). В начальной и конечной точках мы имеем ε(t1) = ε(t2) = 0. Разница между интегралами по пути 1 и по пути 2 равна где мы использовали разложение L до первого порядка по ε и ε′. Теперь используя интегрирование по частям для последнего слагаемого и используя условия ε(t1) = ε(t2) = 0 найдём S достигает стационарной точки, то есть δ S = 0 для каждого ε. Заметим, что точка может быть как минимумом, так и седловой точкой, и даже максимумом, если говорить формально. δ S = 0 для каждого ε если и только если Где мы заменили xa, a = 0,1,2,3 на x, поскольку это выполняется для всех координат. Эта система уравнений называется уравнениями Эйлера-Лагранжа для вариационной задачи. Простое следствие этих уравнений, что если L не зависит явно от x, то есть если Тогда координата x называется циклической координатой, и Например, если L не зависит явно от времени, то соответствующий интеграл движения (сопряжённый импульс) называется энергией. При использовании сферических координат t, r, φ, θ если L не зависит от φ, сохраняющийся сопряжённый импульс — угловой момент. Для тех, кто знаком с функциональным анализом заметим, что уравнения упрощаются Тривиальные примеры помогают оценивать использование принципа действия через уравнения Эйлера-Лагранжа. Свободная частица (масса m и скорость v) в Евклидовом пространстве перемещается по прямой линии. Используя уравнения Эйлера-Лагранжа, это можно показать в полярных координатах следующим образом. В отсутствие потенциала функция Лагранжа просто равна кинетической энергии в ортогональной системе координат (x, y). В полярных координатах (r, φ) кинетическая энергия, и следовательно, функция Лагранжа становится Радиальная компонента r и φ’ уравнений становятся, соответственно Решение этих двух уравнений ряд констант «a, b, c, d» задаётся начальными условиями. Таким образом, действительно, «решение — прямая линия», заданная в полярных координатах. Формализм, приведённый выше, действителен в классической механике в очень ограничительном смысле. Более широко, действие — функционал, задающий отображение из конфигурационного пространства на множество вещественных чисел и, в общем, оно не обязано быть интегралом, потому что нелокальные действия в принципе возможны, по крайней мере, теоретически. Для библиографии с аннотацией смотрите Edwin F. Taylor [2] Среди библиографического списка есть следующие книги МЕХАНИКА — (от греч. mechanike (techne) наука о машинах, искусство построения машин), наука о механич. движении матер. тел и происходящих при этом вз ствиях между ними. Под механич. движением понимают изменение с течением времени взаимного положения тел или … Физическая энциклопедия МЕХАНИКА — (от греч. mechane машина), наука о движении. До 17 века познания в этой области почти ограничивались эмпирическими наблюдениями, часто ошибочными. В 17 веке свойства движения впервые стали выводиться из немногих основных принципов математически.… … Большая медицинская энциклопедия действие по Гамильтону — Величина, равная интегралу по времени от функции Лагранжа для механической системы. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая… … Справочник технического переводчика действие по Лагранжу — Величина, равная интегралу по времени от удвоенной кинетической энергии механической системы. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики… … Справочник технического переводчика Действие (физическая величина) — У этого термина существуют и другие значения, см. Действие (физика). Действие Размерность L2MT−1 Действие в физике скалярная физическая величина, являющаяс … Википедия МЕХАНИКА — раздел физики, в котором изучается движение тел под действием сил. Механика охватывает очень широкий круг вопросов в ней рассматриваются объекты от галактик и систем галактик до мельчайших, элементарных частиц вещества. В этих предельных случаях… … Энциклопедия Кольера Механика — [от греч. mechanike (téchne) наука о машинах, искусство построения машин], наука о механическом движении материальных тел и происходящих при этом взаимодействиях между телами. Под механическим движением понимают изменение с течением… … Большая советская энциклопедия Механика (терминология) — Эта статья содержит список основных определений классической механики. Содержание 1 Кинематика 2 Вращательное дви … Википедия Механика/Основные определения — Предупреждение. Здесь приведены определения некоторых терминов в школьной, элементарной формулировке. При этом некоторыми более сложными эффектами может быть пренебрежено. Содержание 1 Кинематика 2 Вращательное движение тела вокруг неподвижной… … Википедия Действие — I Действие физическая величина, имеющая размерность произведения энергии на время и являющаяся одной из существенных характеристик движения системы. Для механической системы Д. обладает следующим важным свойством: если рассмотреть… … Большая советская энциклопедия Что такое действие и почему физики все время о нем говорят Как современные физики-теоретики разрабатывают новые теории, описывающие мир? Что такого они добавляют к квантовой механике и общей теории относительности, чтобы построить «теорию всего»? О каких ограничениях идет речь в статьях, говорящих про отсутствие «новой физики»? На все эти вопросы можно ответить, если разобраться, что такое действие — объект, лежащий в основе всех существующих физических теорий. В этой статье я расскажу, что физики понимают под действием, а также покажу, как с его помощью можно построить настоящую физическую теорию, используя всего несколько простых предположений о свойствах рассматриваемой системы. Сразу предупреждаю: в статье будут формулы и даже несложные вычисления. Впрочем, их вполне можно пропускать без большого вреда для понимания. Вообще говоря, я привожу здесь формулы только для тех заинтересованных читателей, которые непременно хотят разобраться во всем самостоятельно. Физика описывает наш мир с помощью уравнений, связывающих вместе различные физические величины — скорость, силу, напряженность магнитного поля и так далее. Практически все такие уравнения являются дифференциальными, то есть содержат не только функции, зависящие от величин, но и их производные. Например, одно из самых простых уравнений, описывающее движение точечного тела, содержит вторую производную от его координаты: Однако как же физики находят эти дифференциальные уравнения? В течение долгого времени единственным источником новых теорий был эксперимент. Другими словами, первым делом ученый проводил измерения нескольких физических величин, и только потом пытался определить, как они связаны. Например, именно таким образом Кеплер открыл три знаменитых закона небесной механики, которые впоследствии привели Ньютона к его классической теории тяготения. Получалось, что эксперимент как будто «бежит впереди теории». В современной же физике дела устроены немного по-другому. Конечно, эксперимент до сих пор играет в физике очень важную роль. Без экспериментального подтверждения любая теория является всего лишь математической моделью — игрушкой для ума, не имеющей отношения к реальному миру. Однако сейчас физики получают уравнения, описывающие наш мир, не эмпирическим обобщением экспериментальных фактов, а выводят их «из первых принципов», то есть на основании простых предположений о свойствах описываемой системы (например, пространства-времени или электромагнитного поля). В конечном счете, из эксперимента определяются только параметры теории — произвольные коэффициенты, которые входят в выведенное теоретиком уравнение. При этом ключевую роль в теоретической физике играет принцип наименьшего действия, впервые сформулированный Пьером Мопертюи в середине XVIII века и окончательно обобщенный Уильямом Гамильтоном в начале XIX века. Что же такое действие? В самой общей формулировке действие — это функционал, который ставит в соответствие траектории движения системы (то есть функции от координат и времени) некоторое число. А принцип наименьшего действия утверждает, что на истинной траектории действие будет минимально. Чтобы разобраться в значении этих умных слов, рассмотрим следующий наглядный пример, взятый из Фейнмановских лекций по физике. Допустим, мы хотим узнать, по какой траектории будет двигаться тело, помещенное в поле тяжести. Для простоты будем считать, что движение полностью описывается высотой x(t), то есть тело движется вдоль вертикальной прямой. Предположим, что мы знаем о движении только то, что тело стартует в точке x1 в момент времени t1 и приходит в точку x2 в момент t2, а полное время в пути составляет T = t2 − t1. Рассмотрим функцию L, равную разности кинетической энергии К и потенциальной энергии П: L = К − П. Будем считать, что потенциальная энергия зависит только от координаты частицы x(t), а кинетическая — только от ее скорости ẋ(t). Также определим действие — функционал S, равный среднему значению L за все время движения: S = ∫ L(x, ẋ, t) dt. Очевидно, что значение S будет существенно зависеть от формы траектории x(t) — собственно, поэтому мы называем его функционалом, а не функцией. Если тело слишком высоко поднимется (траектория 2), вырастет средняя потенциальная энергия, а если оно станет слишком часто петлять (траектория 3), увеличится кинетическая — мы ведь предположили, что полное время движения в точности равно T, а значит, телу нужно увеличить скорость, чтобы успеть пройти все повороты. В действительности функционал S достигает минимума на некоторой оптимальной траектории, которая является участком параболы, проходящей через точки x1 и x2 (траектория 1). По счастливому стечению обстоятельств, эта траектория совпадает с траекторией, предсказанной вторым закон Ньютона. Примеры траекторий, соединяющих точки x1 и x2. Серым отмечена траектория, полученная вариацией истинной траектории. Вертикальное направление отвечает оси x, горизонтальное — оси t Действие в физике — скалярная физическая величина, являющаяся мерой движения физической системы. Действие является математическим функционалом, который берёт в качестве аргумента траекторию движения физической системы и возвращает в качестве результата вещественное число. Принцип наименьшего действия в классической механике постулирует, что физическая система всегда следует траектории с наименьшим действием. В квантовой механике, в формулировке интегралов по траекториям, физическая система одновременно следует всем возможным траекториям, причём амплитуда вероятности следования определённой траектории определяется действием этой траектории. Если характерное действие намного больше постоянной Планка, то амплитуда классической траектории с наименьшим действием является преобладающей — таким образом квантовая механика переходит в классическую. Действие — одна из наиболее фундаментальных физических величин, входящая в современную формулировку большинства основных физических теорий во всех фундаментальных разделах физики, имеющая при этом и огромное техническое значение в теоретической физике. Несколько меньшее значение может иметь в сравнительно более прикладных областях, хотя и там нередко бывает употребительна. Употребляется равно и в квантовой, и в классической, и в релятивистской физике. Имеет физическую размерность энергия · время = импульс · расстояние, совпадающую с размерностью момента импульса. По физическому смыслу действие — фаза квантовой «волны вероятности», точнее — из-за другой размерности в традиционных системах физических единиц (в том числе СИ) — пропорциональна этой фазе: Если для какой-то системы написано действие, то это в принципе определяет и её классическое поведение (то есть поведение системы в классическом приближении), и её квантовое поведение. Первое — через принцип стационарного (наименьшего) действия, второе — через фейнмановский интеграл по траекториям. При этом само действие записывается одинаково, в одной и той же форме, и для классического и для квантового случая, что делает его очень удобным инструментом (для квантования через фейнмановский интеграл в принципе надо знать только действие, определенное для обычных классических траекторий, то есть, записанное так же, как и для классического применения). Исторически терминология довольно сильно колебалась, но в настоящее время принято называть действием величину где (Обе величины в принципе совпадают, но по-разному выражены — первая в соответствии с лагранжевым формализмом, вторая в соответствии с гамильтоновым). Укороченным действием принято называть где обозначения совпадают с использованными выше, а выражение в последнем интеграле — скалярное произведение векторов импульса и скорости, которое в случае одной частицы можно рассматривать в обычном ньютоновском смысле. Вообще в этом пункте под Для распределённых систем (например, для полей или упругих сплошных сред) действие обычно может быть записано так: где С современной точки зрения действие имеет смысл фазы волновой функции (правда, выраженной традиционно — для более прямой связи с классической механикой — в других единицах, а конкретно Классическая физика (механика и теория поля) является высокочастотным и коротковолновым приближением квантовой, когда фазы волн очень велики ( В квантовой же физике — при решении той же задачи без условия Мопертюи в работах 1740(?),1741—1746 гг. впервые сформулировал принцип наименьшего действия для механики и высказал мысль о том, что это универсальный закон природы, проинтерпретировав и оптику (принцип Ферма) в терминах действия (он использовал то, что сейчас принято называть укороченным действием). Мопертюи был склонен к теологической интерпретации этого принципа, свидетельствовавшего, по его мнению, об определенном совершенстве сотворённого Богом мира. Ещё при жизни Мопертюи эти его работы были поддержаны и развиты Эйлером, к тому же разработавшим вариационное исчисление, позволявшее наиболее эффективно реализовать преимущества принципа. Затем Лагранж (в «Аналитической механике» («Mécanique analytique»), опубликованной в 1788 г.) развил применение принципа наименьшего действия в механике, использовав вариационное исчисление и введя обобщённые координаты. Также он изложил в 1795 г. метод неопределенных множителей, позволяющий значительно улучшить использование принципа наименьшего действия в задачах со связями. В 1915 Гильберт, использовав вариационный метод по отношению к действию Эйнштейна-Гильберта, получил верные уравнения гравитационного поля в общей теории относительности. При этом, пожалуй, впервые было в такой полноте использовано преимущество простоты подхода, исходящего из написания из общих соображений скалярного (инвариантного) действия (явный вид которого заранее не известен), а затем — получения уравнений движения для поля (уравнений поля) варьированием этого функционала. В начале XX века Планк, Бор, Зоммерфельд, Шварцшильд и другие использовали действие (обычно укороченное действие) для ранней формулировки квантовой теории, являющейся с современной точки зрения неким вариантом квазиклассического приближения, оказавшейся довольно хорошо подходящей для описания таких ключевых задач, как гармонический осциллятор и атом с круговыми и эллиптическими орбитами электрона (по крайней мере, это касается простейшего случая — атома водорода). Правило квантования, широко использовавшееся на данном этапе развития квантовой теории, сводилось к квантованию укороченного действия на замкнутых орбитах в соответствии с условием Луи де Бройль (1923-1924 гг.) использовал такой формализм для формулировки своих утверждений о волновой природе электрона и вообще материальных частиц. Заметную роль в обосновании современной формы квантовой механики (в смысле выяснения её соотношения с классической) сыграло имеющее дело с действием как функцией координат и времени уравнение Гамильтона — Якоби, уже имеющее форму, близкую к форме основного уравнения квантовой механики — уравнения Шрёдингера — и являющегося при этом по сути его классическим пределом. Фейнман разработал в квантовой механике метод интегрирования по траекториям (1938 год), переформулировавший квантовую механику так, что в ней органически использовался классический функционал действия, а отличие полного квантового описания от классического сводилось к необходимости суммировать величину Начиная со второй половины XX века был изобретен ряд обобщений действия для точечной частицы, например, в области теории струн — действие Намбу — Гото (действие-площадь) и действие Полякова. В заключение следует сказать, что в современных абстрактных областях теоретической физики действие является одним из основных инструментов формулировки конкретной теории уже с начального этапа. Например, один из очень распространенных способов формулировки новой теории сводится к тому, что для исследуемой системы в первую очередь стараются написать действие, ограничивая возможные варианты наложением условий симметрии, и часто — ещё соображениями простоты. Действие в классической механике записывается в двух формах, в конечном итоге эквивалентных: Несмотря на эквивалентность в конечном итоге, лагранжева и гамильтонова форма записи действия обладают не совпадающими техническими и идейными преимуществами. Каждая из них может считаться основой для построения (на основе принципа наименьшего (или стационарного) действия) соответственно лагранжевой и гамильтоновой форм механики. А именно, осуществляя прямое варьирование первого действия по каждому Проводя вывод уравнений движения с подходящим выбором координат (вообще говоря не декартовых) и с использованием метода неопределенных множителей Лагранжа, нетрудно получить в удобном виде и уравнения движения для систем со связями, иногда исключая из них реакции связей (что может заметно упрощать уравнения). Следует заметить, что при всей фундаментальной значимости концепция действия не покрывает некоторых случаев макроскопической механики, например, не позволяет написать действие в случае наличия произвольных диссипативных сил, и соответственно не позволяет воспользоваться для их описания принципом наименьшего действия. Классическое действие — с современной точки зрения — это величина, пропорциональная фазе квантовой волновой функции соответствующей частицы или системы (по сути это и есть фаза, только измеренная в других единицах; однако коэффициент пропорциональности внутри классической механики неизвестен — это существенно квантовая величина, с точки зрения классической механики важно только, что он очень мал). Сама же классическая механика есть коротковолновый предел квантовой, и может быть получена из неё переходом Для механических распределённых систем (например, для упругих сплошных сред) действие обычно может быть записано так: где Для немеханических распределенных систем подобная запись возможна на базе аналогии с механическими. В частности, сходный способ работает для фундаментальных полей, формально также подходящих под определение распределённых систем (хотя можно считать и это лишь аналогией, вопрос того или иного выбора здесь — в сущности терминологический). Подробно фундаментальные физические поля рассмотрены в отдельном параграфе, хотя обычные распределённые системы, механические в особенности, дают в общем достаточно хорошие модели, способствующие пониманию построения динамики этих полей и, в частности, вопросов, связанных с действием. Действие в классической теории поля используется для получения уравнений поля (как свободных, так и с источниками) из принципа стационарного (наименьшего) действия (варьированием по полевым переменным). Также оно используется для получения уравнений движения частиц при взаимодействии с данным полем, также через принцип стационарного (наименьшего) действия, но варьированием уже по координатам (а в гамильтоновом варианте — и по импульсам) частиц. Сам вид действия для поля (применяемого как в классическом, так и в квантовом смысле) в общем очень похож на вид действия для распределённых систем (в частности, для механических распределённых систем, таких, как струна, мембрана и т. п.). Это позволяет установить иногда прямую, иногда условную, аналогию между тем и другим случаем, хотя в деталях то и другое может заметно различаться (так что прямая механическая аналогия возможна не всегда, а иногда её просто оказывается не слишком легко построить и использовать). Чаще всего (в случае линейных полей или изучения их в линейном приближении) действие имеет достаточно простой вид и распадается на три члена: где Среди фундаментальных физических полей скалярные поля, хотя и присутствуют в теории, но пока само их существование носит в значительной мере гипотетический характер, а свойства, соответственно, достаточно плохо известны. Однако это самый простой случай, к тому же, кроме фундаментальных полей представляют интерес такие макроскопические поля, как, например, поле давления газа в акустике, которое в случае малых (и гладких) отклонений от равновесия может быть в известном смысле прямо уподоблено абстрактному скалярному полю. Простейшим видом действия для скалярного поля (записано в форме, соответствующей полю в трёхмерном пространстве; здесь Будучи проварьировано по Стандартное действие для электромагнитного поля записывается так — действие для свободного поля ( член взаимодействия может быть записан по-разному: (первая форма удобна для вывода уравнения (уравнений) поля (с источниками), а второе — для вывода уравнения движения заряженной частицы; здесь где Если же движение частиц медленное по сравнению со скоростью света и достаточно ньютоновского приближения, то можно взять соответствующее приближённое действие, обычное для классической механики: Проще всего получить уравнения Максвелла в форме варьируя записанное выше действие по Варьируя по где правая часть совпадает с обычной силой Лоренца, которая может быть также записана (а при желании и получена явно) и в трёхмерном виде; то есть, в трёхмерном виде уравнение движения будет таким: Действие для электромагнитного поля (и его член для свободного поля, и член, описывающий взяимодействие с токами) с самого начала лоренц-инвариантно. То же можно сказать о действии для всех фундаментальных полей, известных в современных теориях (говоря несколько точнее — в общепризнанных теориях, прошедших экспериментальную проверку). Однако действие классической (ньютоновской) механики, не важно, в какой форме оно записано, гамильтоновой или лагранжевой, не обладает свойством лоренц-инвариантности. Исторически в определенный момент (на грани XIX и XX веков) возникла необходимость привести механику в соответствие с принципом относительности, а значит, сделать её лоренц-ковариантной. Простейший путь для этого — написать для частицы («материальной точки») такое действие, которое бы было лоренц-инвариантным, а затем обычной процедурой варьирования получить из него уравнение движения, которое будет уже лоренц-ковариантным (приближённо, при медленных движений, такая механика должна совпадать с ньютоновской, так как та хорошо проверена для малых скоростей). Простейшее действие для свободной частицы, которое можно предложить, исходя из геометрии Минковского, — это величина, с точностью до постоянного множителя совпадающая с длиной мировой линии данной частицы (а соображения размерности определят коэффициент): где Разложив где первый член можно отбросить, так как он не даёт никакого вклада в уравнения движения (за исключением вклада в уравнения гравитационного поля, в которых его влияние не исчезает даже в этом приближении; здесь же идет речь об уравнениях движения самой частицы, для которой написано действие, а гравитация в эйнштейновском смысле не рассматривается). При желании можно в проделанном разложении сохранить и члены следующих порядков по Для ньютоновской теории тяготения действие можно бы было записать как Поэтому здесь ограничимся тем, что приведем действие, соответствующее основной (неквантовой) теории гравитации современной физики — общей теории относительности. Это действие Эйнштейна — Гильберта: где Варьированием этого действия по метрике (именно таким образом их получил впервые в 1915 году Гильберт, Эйнштейн шёл другим путём). Член уравнения, описывающий источник гравитационного поля (правая часть) получается при этом потому, что метрика Действие для гравитационного поля ОТО может быть переписано и в другом виде, эквивалентном данному за исключением граничных условий (а если граничные почему-либо обнуляются, то в полностью эквивалентном), и содержащем под интегралом вместо тензора кривизны конструкцию из Дополняя же написанное выше действие членом Вполне удовлетворительной квантовой теории гравитации, насколько известно, в настоящее время (2009 год) не существует. Однако многие из теорий, которые с большим или меньшим основанием могут претендовать на эту роль, дают обычно эффективное действие Эйнштейна — Гильберта в низкоэнергетическом пределе. Для фермионных (в частности, для спинорных) полей можно не только написать действие, но и получить формально классические уравнения для этих полей, варьируя такое действие. Однако в отличие от бозонных, фермионные поля наблюдаемы в их классическом виде хуже, так как принцип Паули запрещает более чем одному фермиону находиться в одном состоянии, что разрешено для бозонов и позволяет им, находясь в одинаковом квантовом состоянии в большом количестве, наблюдаться как обычное классическое поле, например, электромагнитное. Но при этом есть теорема, утверждающая (по крайней мере в рамках применимости теории возмущений), что результат вторичного квантования для таких фермионных полей совпадает с интерпретацией таких «классических» полей как волновых функций фермионов в смысле первичного квантования. Таким образом, например, полученное с помощью принципа стационарного действия из той или иной формы записи действия для частицы со спином 1/2 уравнение Дирака имеет прямое отношение к квантовому описанию такого фермиона (например, электрона). У уравнения Дирака есть свойство, представляющее определённую трудность для получения его из действия с квадратичным лагранжианом (да и каким-либо иным, если пользоваться обычными правилами варьирования и считать компоненты спиноров обычными числами). Это свойство — первый порядок производных в уравнении Дирака. Из положения иногда выходят, просто введя искусственные формальные модификации ограничения на правила варьирования или действия операторов производных. Более систематический, по-видимому, подход заключается в том, что фермионные поля (спиноры и их компоненты) считаются грассмановыми, то есть антикоммутирующими числами, что меняет знак членов с производными первого и второго порядка по сравнению с обычным, из-за чего члены второго порядка при варьировании уничтожаются, а первого остаются. Фейнмановский интеграл по траекториям применим к квантовому описанию как точечных частиц в обычном пространстве, так и полей (как распределенных систем) в конфигурационном пространстве (и эта применимость к обоим случаям в принципе неудивительна, поскольку формальное отличие между точечной частицей и многомерной, даже бесконечномерной, динамической системой — лишь в размерности конфигурационного пространства, что в целом хорошо понятно уже в рамках классической механики). Если действие S[x] (в сущности, совпадающее с обычным классическим действием, по крайней мере для систем, описание которых не настолько экзотично, чтобы затруднять такое словоупотребление) известно, то есть его можно написать для обычной классической траектории где x — траектория, начинающаяся в В квантовой теории поля применяется интегрирование как по траекториям частиц в обычном пространстве (точнее, в пространстве-времени), которое обычно называют в этом случае первичным квантованием, так и по траекториям в пространстве полевых переменных, что называется вторичным квантованием. Тот и другой способ, насколько известно, дает эквивалентные результаты в рамках теории возмущений. Фейнмановский интеграл по траекториям — один из наиболее популярных у современных физиков-теоретиков способов квантования (построения квантовой теории). Одновременно это один из наиболее прямых способов сопоставления квантовой картины с классической, что является одним из серьёзных его психологических преимуществ, так как каждая траектория в нём в принципе воспринимается как классическая, а действие вычисляется в точности по классическому рецепту, что в ряде случаев и аспектов делает теорию заметно более обозримой и легко понимаемой, чем другие подходы. В числе прочего это свойство удобно для осуществления предельного перехода к классике (см. ниже), и переход к ней исходя из интеграла по траекториям является в этом смысле одним из наиболее стандартных путей в современной физике. То же относится и к достаточному удобству получения таким путем квазиклассического приближения (также см. ниже). В ряде случаев (весьма ограниченном — когда действие квадратично по координатам или полевым переменным и их производным, и интеграл сводится к многомерному гауссову с предельным переходом к бесконечномерному случаю) фейнмановский интеграл по траекториям может быть вычислен явно и точно. Практикуется его расчёт численными методами. Во многих случаях этот интеграл полезен в различных преобразованиях и прочих теоретических расчётах. Нетрудно установить эквивалентность подхода интегрирования по траекториям уравнению Шрёдингера, по крайней мере при тривиальной топологической ситуации. Для свободных (не взаимодействующих друг с другом) полей на пустом плоском пространстве интегрирование по траекториям позволяет часто получить в явном виде пропагатор, который оказывается совпадающим с пропагатором, получаемым из дифференциального уравнения для соответствующего поля (например, из волнового уравнения для безмассового скалярного поля). При этом оказывается, что для взаимодействующих полей интеграл по траекториям является, пожалуй, наиболее естественным (и популярным среди современных теоретиков) способом обоснования техники диаграмм Фейнмана. Дело в том, что интеграл по траекториям для системы взаимодействующих частиц (полей) легко разбивается на части, где взаимодействия нет (а результат, как мы говорили чуть выше, для этого случая известен — это пропагатор, соответствующий поведению свободного поля, который может быть довольно легко вычислен любым способом), дополненные точечным взаимодействием, которое уже сводится к обычному конечномерному интегрированию — в соответствии с правилами Фейнмана. Однако квантование с помощью интеграла по траекториям не ограничено теорией возмущений (диаграммами Фейнмана). Этот способ находит и более нетривиальные применения, как в теоретической физике, так и в некоторых областях чистой математики. [4] [5] [6]Размерность L 2 MT −1 Единицы измерения СИ Дж·с СГС эрг·с Примечания скалярная величина Действие (механика)
Содержание
Некоторые применения принципа действия
История
Принцип действия в классической механике
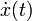
Уравнения Эйлера-Лагранжа для интеграла действия
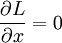
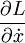
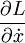
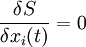
Пример: свободная частица в полярных координатах
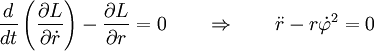
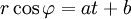
Смотрите также
Литература на русском языке
Литература
Внешние ссылки
Полезное
Смотреть что такое «Действие (механика)» в других словарях:
На пути к теории всего
Уравнения
Действие
Действие (физическая величина)

Содержание
Терминология












Общий обзор






История



Действие в классической механике





Действие для распределённых систем









Действие в классической теории поля






Скалярное поле














Электромагнитное поле



























Релятивистское действие











Действие в теории гравитации
















Действие и квантовая механика
Действие для фермионных полей
Фейнмановский интеграл по траекториям