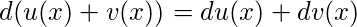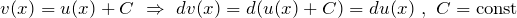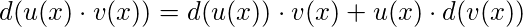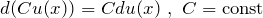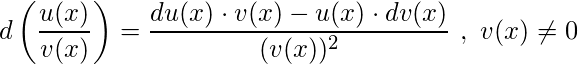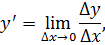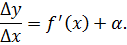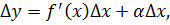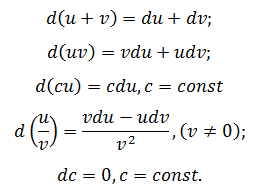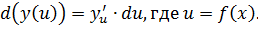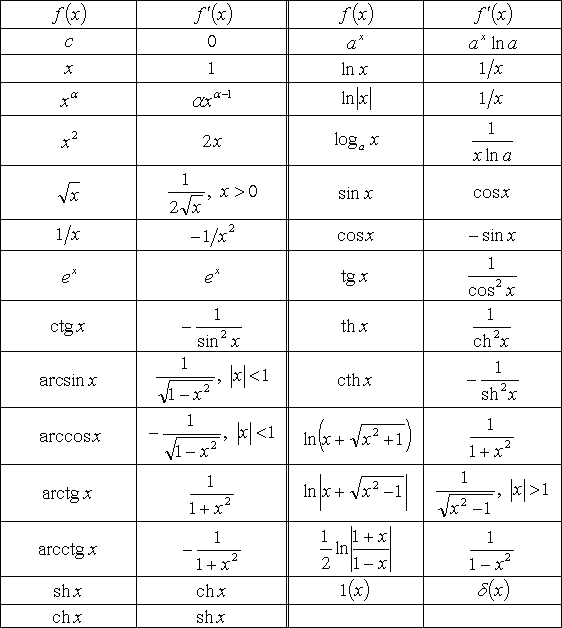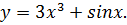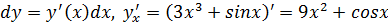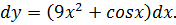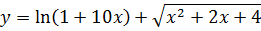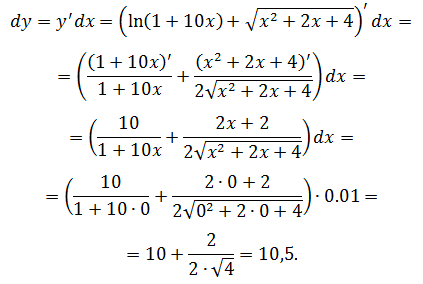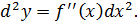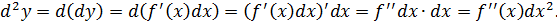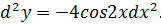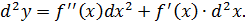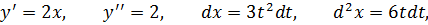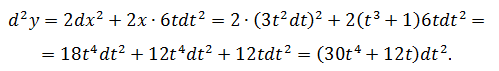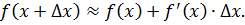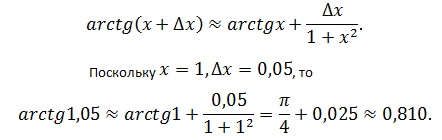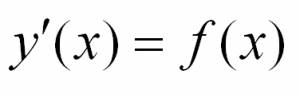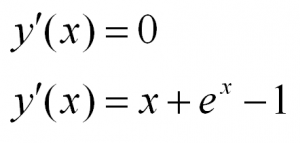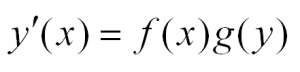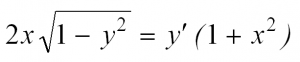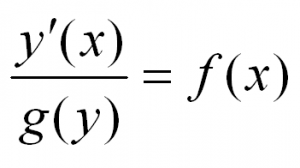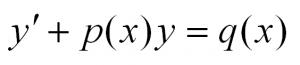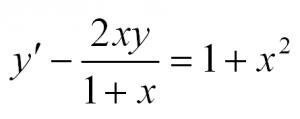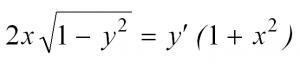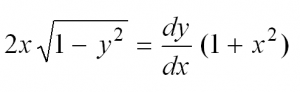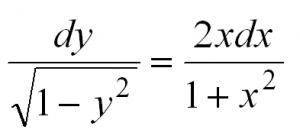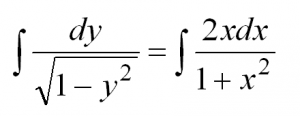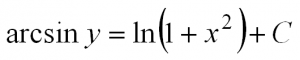Дифференциал нуля чему равен
Свойства дифференциалов
1. Дифференциал константы равен нулю:
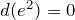 |
2. Дифференциал суммы функций равен сумме дифференциалов слагаемых:
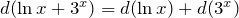 |
Следствие. Если две функции отличаются на константу, то их дифференциалы равны:
3. Дифференциал произведения двух функций равен произведению дифференциала первой функции на вторую плюс первая функция на дифференциал второй:
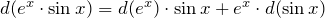 |
Следствие. Постоянный множитель можно выносить за знак дифференциала:
4. Дифференциал частного двух функций 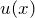
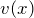
5. Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной функции на дифференциал аргумента независимо от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.
Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.
При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции. Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.
Понятие и геометрический смысл дифференциала
Пусть y = f (x) имеет производную
Применяя свойства предела функции, получают равенство
После умножения обеих частей на приращение аргумента Δx, образуется тождество:
в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.
Определение 1
Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).
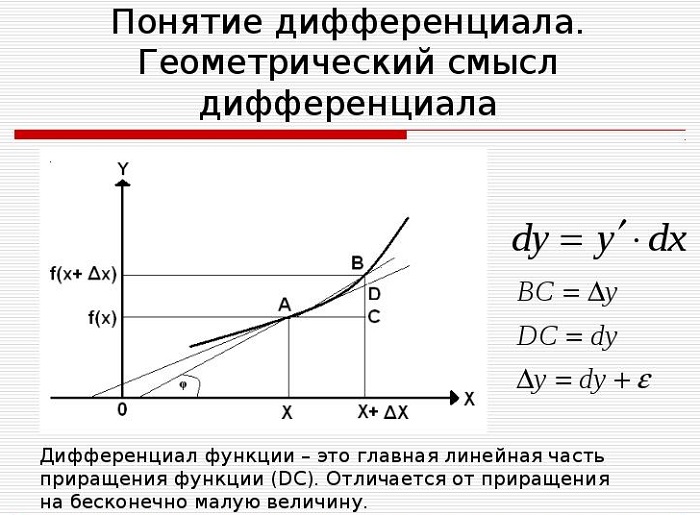
Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.
Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.
Определение 2
Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.
Формы записи дифференциала
Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:
Отсюда получается формула:
Для второго порядка вводится обозначение d 2 y.
Свойства дифференциала
Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:
Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,
Примеры решения задач
Задача №1
Найти дифференциал функции
Задача №2
Вычислить значение дифференциала функции
В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.
Если dx есть константа, то для высших порядков имеет место следующая формула:
Этот результат вытекает непосредственно из определения:
Задача №3
Найти d 2 y, если y = cos2x и x – независимая переменная.
Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,
Задача №4
Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.
Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.
с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.
Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:
Задача №5
Вычислить приближённо arctg1,05.
Пусть f(x) = arctg x. Тогда
Полный дифференциал функции
Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.
Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.
Например, если z = f(x;y) то
Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.
Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.
Заключение
Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.
Дифференциал функции определение, виды, свойства, формула полного дифференциала функции, геометрический смысл, правило применения, примеры решения уравнений
При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции.
Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.
Понятие и геометрический смысл дифференциала
Пусть y = f (x) имеет производную
Применяя свойства предела функции, получают равенство
После умножения обеих частей на приращение аргумента Δx, образуется тождество:
в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.
Определение 1
Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).
Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.
Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.
Определение 2
Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.
Формы записи дифференциала
Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:
Отсюда получается формула:
Для второго порядка вводится обозначение d 2 y.
Свойства дифференциала
Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:
Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,
Примеры решения задач
Задача №1
Найти дифференциал функции
Задача №2
Вычислить значение дифференциала функции
В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.
Если dx есть константа, то для высших порядков имеет место следующая формула:
Этот результат вытекает непосредственно из определения:
Задача №3
Найти d 2 y, если y = cos2x и x – независимая переменная.
Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,
Задача №4
Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.
Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.
с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.
Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:
Задача №5
Вычислить приближённо arctg1,05.
Пусть f(x) = arctg x. Тогда
Полный дифференциал функции
Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.
Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.
Например, если z = f(x;y) то
Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.
Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.
Заключение
Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.
Дифференциальные уравнения для «чайников». Примеры решения
Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?
Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.
Основные понятия теории дифференциальных уравнений
Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.
Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.
Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.
Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.
Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.
Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.
Порядок дифференциального уравнения определяется наивысшим порядком производных, входящих в него.
Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.
Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:
Решить такое уравнение можно, просто проинтегрировав его правую часть.
Примеры таких уравнений:
Уравнения с разделяющимися переменными
В общем виде этот тип уравнений выглядит так:
Решая такое уравнение, нужно разделить переменные, приведя его к виду:
После этого останется проинтегрировать обе части и получить решение.
Линейные дифференциальные уравнения первого порядка
Такие уравнения имеют вид:
Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:
Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).
Для решения таких уравнений необходима определенная подготовка и взять их “с наскока” будет довольно сложно.
Пример решения ДУ с разделяющимися переменными
Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.
Сначала перепишем производную в более привычном виде:
Затем разделим переменные, то есть в одной части уравнения соберем все «игреки», а в другой – «иксы»:
Теперь осталось проинтегрировать обе части:
Интегрируем и получаем общее решение данного уравнения:
Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Дифференциал нуля чему равен
Заметим, что в данном примере коэффициент \(A\) равен значению производной функции \(S\) в точке \(
Коэффициент \(A\) главной части приращения функции в точке \(
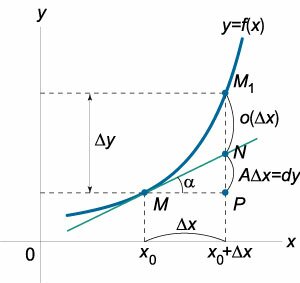
На рисунке \(2\) схематически показана разбивка приращения функции \(\Delta y\) на главную часть \(A\Delta x\) (дифференциал функции) и член высшего порядка малости \(\omicron\left( <\Delta x>\right)\).
Касательная \(MN\), проведенная к кривой функции \(y = f\left( x \right)\) в точке \(M\), как известно, имеет угол наклона \(\alpha\), тангенс которого равен производной: \[\tan \alpha = f’\left( <