Дифференцирующая цепь для чего нужна
Что такое дифференцирующие и интегрирующие цепи?
Активные на ОУ и пассивные RC и RL дифференцирующие и интегрирующие цепи: схемы, осциллограммы и онлайн калькулятор расчёта постоянной времени цепи.
Святая простота! Что может быть проще?
А проще могут быть лишь чётко сформулированные определения дифференцирующей и интегрирующей цепей, не обременённые ни лингвистическими излишествами, ни всякого рода необязательными формулами.
Начнём с RC и RL дифференцирующих цепей.
Эти цепи решают две основные задачи преобразования сигналов:
1. Формирование импульсов малой длительности (укорочение входных импульсов), которые далее используются для запуска триггеров, одновибраторов и других устройств,
2. Выполнение математической операции дифференцирования (получение производной по времени) для устройств вычислительной техники, аппаратуры авторегулирования и т.д.
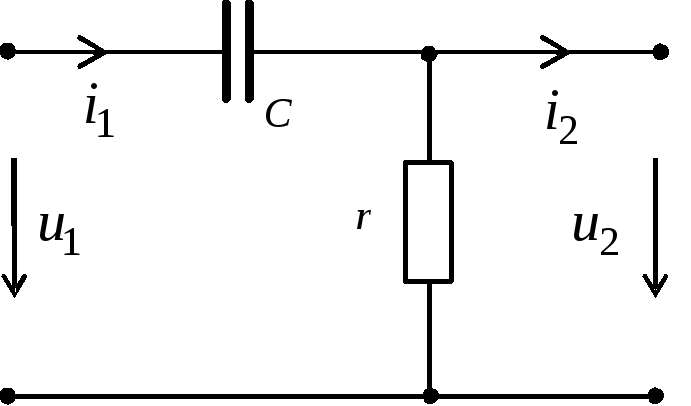
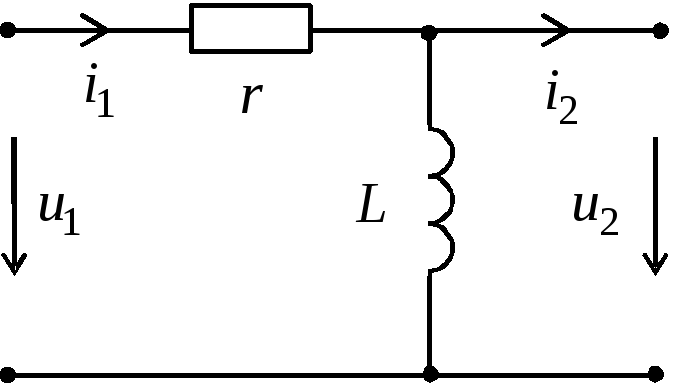
Рис.1.
Основной характеристикой данных цепей является постоянная времени цепи τ = rC, либо τ = L/r.
В общем случае сигнал на выходе цепи описывается следующей формулой:
U2 = τ ×d(U1-U2)/dt.
Однако на практике, если мы выбираем τ τ ×dU1/dt.
Приведём несколько поясняющих картинок.
На Рис.2 приведены осциллограммы напряжений на выходах дифференцирующих цепей, в зависимости от различных соотношений постоянной времени цепи τ и длительности входного импульса tи.
Переходим к интегрирующим RC и RL цепям.
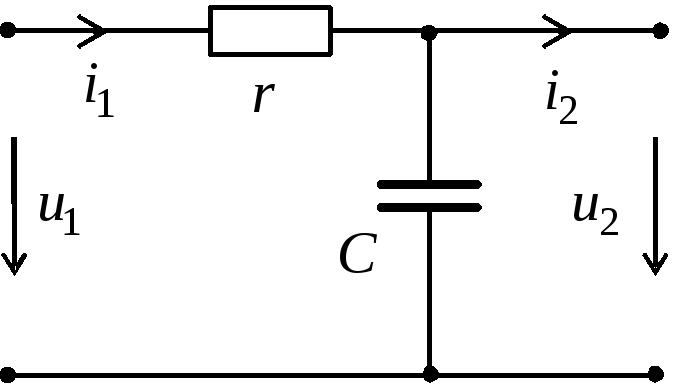
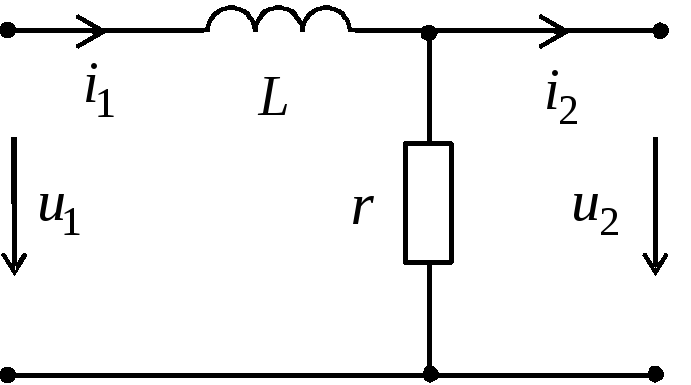
Рис.3.
Значение величины постоянной времени интегрирующей цепи ничем не отличается от дифференцирующих собратьев: τ = rC, либо τ = L/r.
Продолжим уроки рисования.
На Рис.4 приведены осциллограммы напряжений на выходах интегрирующих цепей, в зависимости от различных соотношений постоянной времени цепи τ и длительности входного импульса tи.
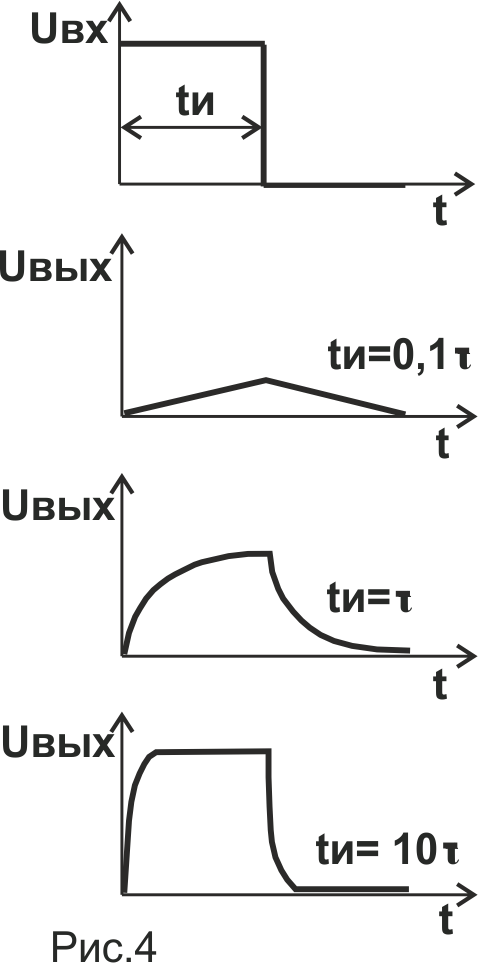
Снять ограничения по выбору постоянной времени дифференцирующих и интегрирующих цепей (по отношению к длительности входного импульса) можно посредством применения операционных усилителей (Рис.5).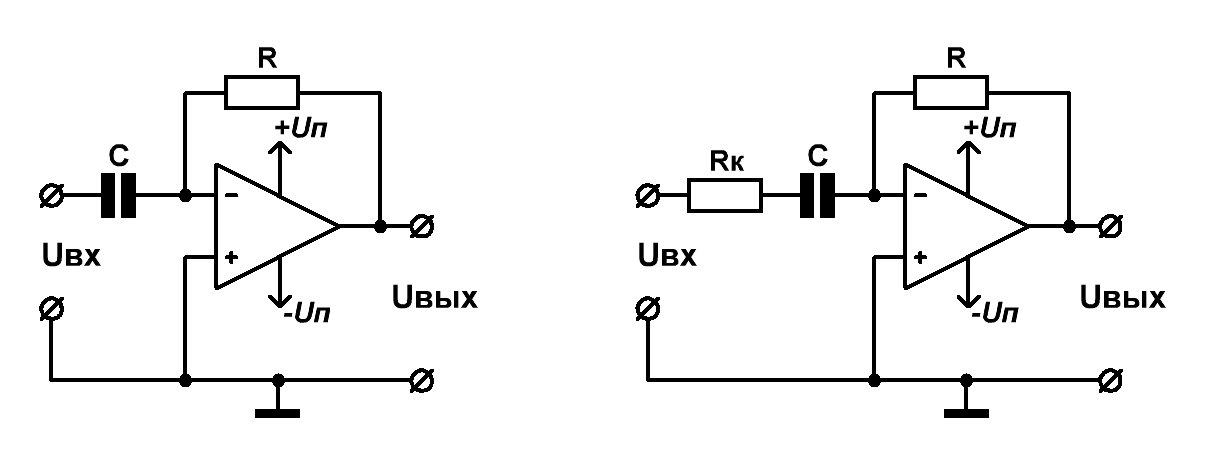 
Рис.5 Схемы активных дифференциаторов на ОУ
Здесь всё по аналогии с пассивными цепями, только без ограничений по длительности входного импульса и, поскольку включение операционного усилителя инвертирующее – со знаком минус:
Uвых = – RC×dUвх/dt.
Уменьшение реактивного сопротивления конденсатора С при росте частоты приводит к синхронному повышению коэффициента усиления активного дифференциатора, что создаёт условия для возможного самовозбуждения устройства. Для того, чтобы этого избежать в схему активного дифференциатора часто вводят корректирующее сопротивление Rк (Рис.5 справа). Применение данного резистора ограничивает коэффициент усиления на BЧ, что, в свою очередь, обеспечивает более высокую динамическую устойчивость.
Для того чтобы не сильно пострадала точность преобразования, номинал корректирующего резистора Rк следует выбрать небольшим, как минимум в 100 раз меньшим, чем величина сопротивления резистора R.
Переходим к схемам интеграторов, построенных на операционных усилителях (Рис.6).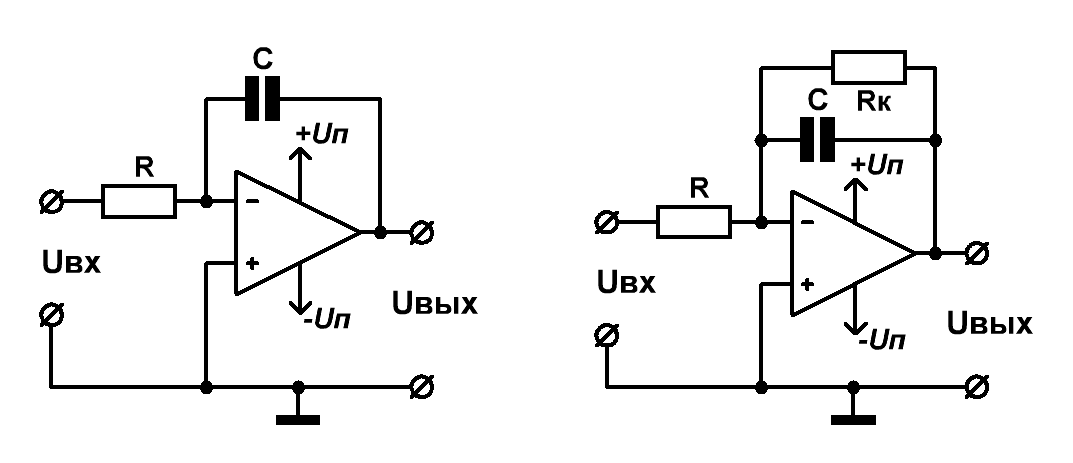 
Рис.6 Схемы активных интеграторов на ОУ
Здесь тоже всё без изменений: Uвых = – ∫Uвхdt / (RC).
В отличие от дифференциатора, схема интегрирующего усилителя имеет высокую устойчивость, но за счёт отсутствия обратной связи по постоянному току, имеет склонность к дрейфу выходного напряжения. Связано это с ненулевым значением параметра смещения выходного уровня реального ОУ.
Ошибку напряжения сдвига можно уменьшить посредством включения параллельно конденсатору С корректирующего резистора Rк (Рис.6 справа), образующего совместно с входным резистором R ООС по постоянному току. Для сохранения точности преобразования номинал Rк как минимум в 100 раз должен превышать сопротивление резистора R.
3.2. ДИФФЕРЕНЦИРУЮЩИЕ ЦЕПИ
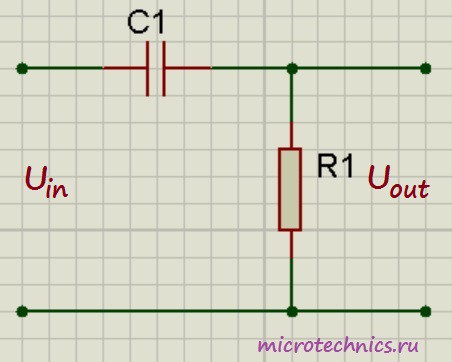
Сложные радиоэлектронные устройства состоят из простых цепей. Рассмотрим цепь, состоящую из резистора и конденсатора, включенных последовательно с идеальным генератором напряжения, показанную на рис. 3.3.
Рис.3.3. Дифференцирующая цепь
Если выходное напряжение снимается с резистора, то цепь называется дифференцирующей, если с конденсатора – интегрирующей. Эти линейные цепи характеризуются стационарными и переходными характеристиками. Это связано с тем, что изменение величины действующего в цепи напряжения приводит к тому, что токи и напряжения в различных участках цепи приобретают новые значения. Изменение состояния цепи происходит не мгновенно, а в течение некоторого интервала времени. Поэтому различают установившееся и переходное состояние электрической цепи.
Электрические процессы считаются установившимися (стационарными), если закон изменения всех напряжений и токов совпадает с точностью до постоянных величин с законом изменения действующего в цепи напряжения от внешнего источника. В противном случае считают, что цепь находится в переходном (нестационарном) состоянии.
К стационарным характеристикам относятся амплитудно-частотная и фазовая характеристики линейной цепи.
Нестационарное состояние линейной цепи описывается переходной характеристикой.
Будем считать, что к входу цепи подключен идеальный генератор напряжения 
. На основании второго закона Кирхгофа для дифференцирующей цепи можно записать дифференциальное уравнение, связывающее напряжения и ток в ветвях цепи:
(3.2)
Так как напряжение на выходе цепи 
, то:
(3.3)
Подставляя в интеграл значение тока, получим:
(3.4)
Продифференцируем левую и правую части последнего уравнения по времени:
(3.5)
Перепишем это уравнение, в следующем виде:
, (3.6)
Где 
=
— параметр цепи называемый постоянной времени цепи.
В зависимости от величины постоянной времени возможны два различных соотношения между первым и вторым слагаемыми правой части уравнения.
Если постоянная времени большая по сравнению с периодом гармонических сигналов 
>>
Или с длительностью импульсов >>
, которые можно подавать на вход этой цепи, то
(3.7)
И напряжение на выходе цепи с небольшими искажениями повторяет входное напряжение:
. (3.8)
Дифференцирующая и интегрирующая электрические цепи
Рассмотрим электрическую цепь из резистора сопротивлением R и конденсатора ёмкостью C.
Элементы R и C соединены последовательно, значит, ток в их цепи можно выразить, исходя из производной напряжения заряда конденсатора dQ/dt = C(dU/dt) и закона Ома U/R. Напряжение на выводах резистора обозначим UR. Тогда будет иметь место равенство:
Проинтегрируем последнее выражение
Интеграл левой части уравнения будет равен Uout + Const.
Перенесем постоянную составляющую Const в правую часть с тем же знаком. В правой части постоянную времени RC вынесем за знак интеграла
В итоге получилось, что выходное напряжение Uout прямопропорционально интегралу напряжения на выходах резистора, следовательно, и входному току Iin.
Здесь t – время заряда или разряда конденсатора в пределах периода.
τ = RC – постоянная времени – произведение величин R и C.
Если взять номиналы RC цепи, когда τ будет значительно больше t, тогда начальный участок экспоненты для короткого периода (относительно τ) может быть достаточно линейным, что обеспечит необходимую пропорциональность между входным напряжением и током. Для простой цепи RC постоянную времени обычно берут на 1-2 порядка больше периода переменного входного сигнала, тогда основная и значительная часть входного напряжения будет падать на выходах резистора, обеспечивая в достаточной степени линейную зависимость Uin/Iin ≈ R.
В таком случае выходное напряжение Uout будет с допустимой погрешностью пропорционально интегралу входного Uin. Чем больше величины номиналов RC, тем меньше переменная составляющая на выходе, тем более точней будет кривая функции. В большинстве случаев, переменная состовляющая интеграла не требуется при использовании таких цепей, нужна только постоянная Const, тогда номиналы RC можно выбирать по возможности большими, но с учетом входного сопротивления следующего каскада.
В качестве примера, сигнал с генератора – положительный меандр 1V периодом 2 mS подадим на вход простой интегрирующей цепи RC с номиналами:
R = 10 kOhm, C = 1uF. Тогда τ = RC = 10 mS.
В данном случае постоянная времени лишь в пять раз больше времени периода, но визуально интегрирование прослеживается в достаточной степени точно. График показывает, что выходное напряжение на уровне постоянной состовляющей 0.5 будет треугольной формы, потому как участки, не меняющиеся во времени, для интеграла будут константой (обозначим её α), а интеграл константы будет линейной функцией. ʃαdx = αx + Const. Величина константы α определит тангенса угла наклона линейной функции.
Если подать на вход сигнал треугольной формы, на выходе будет синусоидальное напряжение. Интеграл линейного участка функции – парабола. В простейшем варианте ʃxdx = x 2 /2 + Const. Знак множителя определит направление параболы.
Недостаток простейшей цепочки в том, что переменная составляющая на выходе получается очень маленькой относительно входного напряжения.
Для простейшей дифференцирующей цепочки RC из двух элементов используем пропорциональную зависимость выходного напряжения от производной напряжения на выводах конденсатора.
Если взять номиналы элементов RC, чтобы постоянная времени была на 1-2 порядка меньше длины периода, тогда отношение приращения входного напряжения к приращению времени в пределах периода может определять скорость изменения входного напряжения в определенной степени точно. В идеале это приращение должно стремится к нулю. В таком случае основная часть входного напряжения будет падать на выводах конденсатора, а выходное будет составлять незначительную часть от входного, поэтому для вычислений производной такие схемы практически не используются.
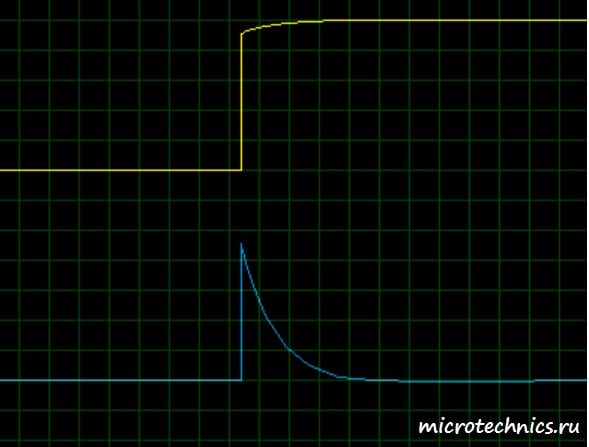
На выходе дифференцирующей цепи амплитудное напряжение после подачи импульса появляется мгновенно, так как на выводах разряженного конденсатора оно равно нулю. Далее следует процесс заряда и напряжение на выводах резистора убывает. За время 3τ оно уменьшится до 5% амплитудного значения.
5% – величина показательная. В практических расчетах этот порог определится входными параметрами применяемых логических элементов.
RC-цепь. Дифференцирующие и интегрирующие RC-цепи.
Обсудив в предыдущих статьях устройство и принцип работы резисторов, конденсаторов и катушек индуктивности, мы имеем полное право перейти к рассмотрению цепей, состоящих из этих элементов! Этим мы сегодня и займемся. И первая RC-цепь, работу которой мы рассмотрим…
Дифференцирующая RC-цепь.
Из названия цепи, в принципе, уже понятно, что за элементы входят в ее состав — это конденсатор и резистор 🙂 И выглядит она следующим образом:
Работа данной схемы основана на том, что ток, протекающий через конденсатор, прямо пропорционален скорости изменения напряжения, приложенного к нему:
Напряжения в цепи связаны следующим образом (по закону Кирхгофа):
В то же время, по закону Ома мы можем записать:
Выразим u_c из первого выражения и подставим во второе:
При условии, что C R\medspace\frac
Таким образом, цепь полностью оправдывает свое название, ведь напряжение на выходе представляет из себя дифференциал входного сигнала. Но возможен еще и другой случай, когда C R\medspace\frac
То есть: U_
Давайте разберемся, какой смысл несет в себе эта характеристика цепи 🙂 Заряд и разряд конденсатора происходит по экспоненциальному закону:
Здесь U_0 — напряжение на заряженном конденсаторе в начальный момент времени. Теперь посмотрим, каким будет значение напряжения по истечении времени \tau :
Напряжение на конденсаторе уменьшится до 37% от первоначального. Таким образом, \tau — это время, за которое конденсатор:
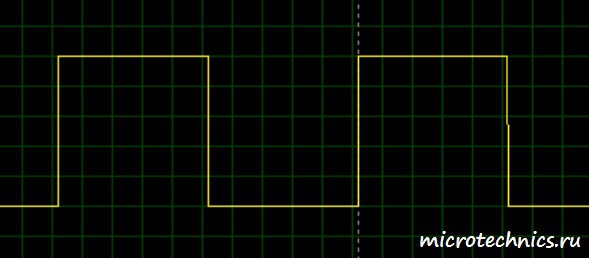
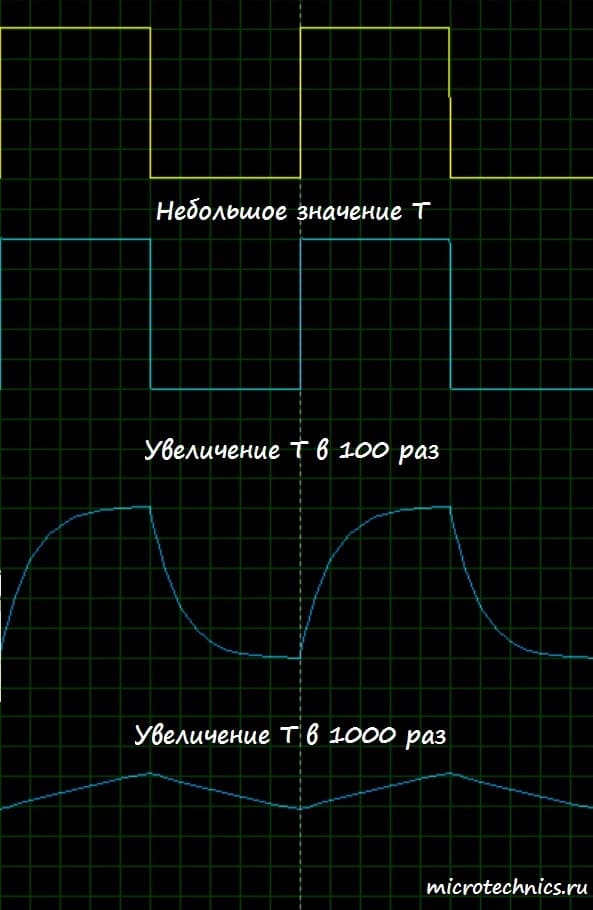
С постоянной времени цепи мы разобрались, давайте вернемся к дифференцирующей RC-цепи. Теоретические аспекты функционирования мы разобрали, так что давайте посмотрим, как она работает на практике. А для этого попробуем подавать на вход какой-нибудь сигнал и посмотрим, что получится на выходе. В качестве примера, подадим на вход последовательность прямоугольных импульсов:
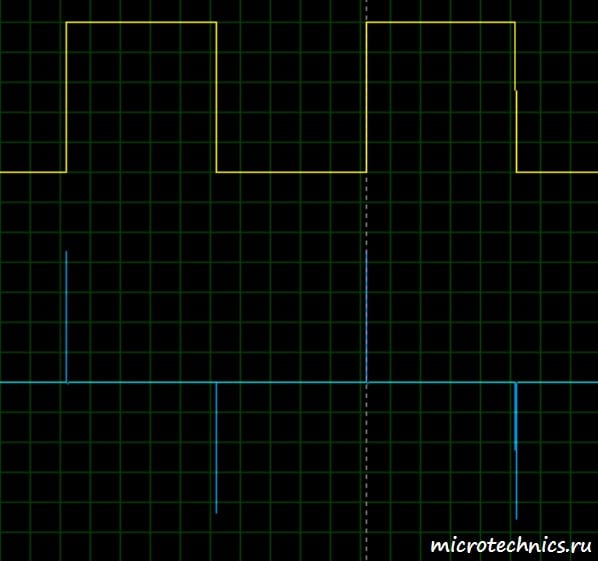
А вот как выглядит осциллограмма выходного сигнала (второй канал — синий цвет):
Что же мы тут видим?
При «отключении» сигнала на входе дифференцирующей цепи происходит аналогичный переходный процесс, но только вызван он не зарядкой, а разрядкой конденсатора.
В данном случае постоянная времени цепи у нас имеет небольшую величину, поэтому цепь хорошо дифференцирует входной сигнал. По нашим теоретическим расчетам, чем больше мы будем увеличивать постоянную времени, тем больше выходной сигнал будет похож на входной. Давай проверим это на практике! Будем увеличивать сопротивление резистора, что и приведет к росту \tau :
Тут даже не надо ничего комментировать — результат налицо 🙂 Мы подтвердили теоретические выкладки, проведя практические эксперименты, так что давайте переходить к следующему вопросу — к интергрирующим RC-цепям.
Интегрирующая RC-цепь.
Запишем выражения для вычисления тока и напряжения данной цепи:
В то же время ток мы можем определить из Закона Ома:
Приравниваем эти выражения и получаем:
Проинтегрируем правую и левую части равенства:
Как и в случае с дифференцирующей RC-цепочкой здесь возможны два случая:
Для того, чтобы убедиться в работоспособности цепи, давайте подадим на ее вход точно такой же сигнал, какой мы использовали при анализе работы дифференцирующей цепи, то есть последовательность прямоугольных импульсов. При малых значениях \tau сигнал на выходе будет очень похож на входной сигнал, а при больших величинах постоянной времени цепи, на выходе мы увидим сигнал, приближенно равный интегралу входного. А какой это будет сигнал? Последовательность импульсов представляет собой участки равного напряжения, а интеграл от константы представляет из себя линейную функцию ( \int Cdx = Cx ). Таким образом, на выходе мы должны увидеть пилообразное напряжение. Проверим теоретические выкладки на практике:
Желтым цветом здесь изображен сигнал на входе, а синим, соответственно, выходные сигналы при разных значениях постоянной времени цепи. Как видите, мы получили именно такой результат, который и ожидали увидеть 🙂
На этом мы и заканчиваем сегодняшнюю статью, но не заканчиваем изучать электронику, так что до встречи в новых статьях!
RC цепь
R — это резистор, С — конденсатор, а вместе они образуют RC-цепь, то есть это цепь, которая состоит из конденсатора и резистора. Все просто 😉
Принцип работы RC цепи
Как вы помните, конденсатор представляет из себя две обкладки на некотором расстоянии друг от друга.
Вы, наверное, помните, что его емкость зависит от площади обкладок, от расстояния между ними, а также от вещества, которое находится между обкладками. Или формулой для плоского конденсатора:
Ладно, ближе к делу. Пусть у нас имеется конденсатор. Что с ним можно сделать? Правильно, зарядить 😉 Для этого берем источник постоянного напряжения и подаем заряд на конденсатор, тем самым заряжая его:
В результате, у нас конденсатор зарядится. На одной обкладке будет положительный заряд, а на другой обкладке — отрицательный:
Даже если убрать батарею, у нас заряд на конденсаторе все равно сохранится в течение какого-то времени.
Сохранность заряда зависит от сопротивления материала между пластинами. Чем оно меньше, тем быстрее со временем будет разряжаться конденсатор, создавая ток утечки. Поэтому самыми плохими, в плане сохранности заряда, являются электролитические конденсаторы, или в народе — электролиты:
Но что произойдет, если к конденсатору мы подсоединим резистор?
Конденсатор разрядится, так как цепь станет замкнутой. Разряжаться он будет через резистор. В разряде конденсатора через резистор и заложен весь принцип работы RC цепочки.
Постоянная времени RC-цепи
Но дело в том, что мы не можем наблюдать процесс разрядки конденсатора, просто посмотрев на RC цепь. Для этого нам понадобится цифровой осциллограф с функцией записи сигнала. Благо на моем рабочем столе уже есть место этому прибору:
Итак, план действий будет такой: мы будем заряжать конденсатор с помощью блока питания, а потом разряжать его на резисторе и смотреть осциллограмму, как разряжается конденсатор.
Соберем классическую схему, которая есть в любом учебнике по электронике:
в этот момент мы заряжаем конденсатор
потом переключаем тумблер S в другое положение и разряжаем конденсатор, наблюдая процесс разряда конденсатора на осциллографе
Думаю, с этим все понятно. Ну что же, приступим к сборке.
Берем макетную плату и собираем схемку. Конденсатор я взял емкостью в 100мкФ, а резистор 1 КилоОм.
Вместо тумблера S я буду вручную перекидывать желтый проводок.
Ну все, цепляемся щупом осциллографа к резистору
и смотрим осциллограмму, как разряжается конденсатор.
Те, кто впервые читает про RC-цепи, думаю, немного удивлены. По логике, разряд должен проходить прямолинейно, но здесь мы видим загибулину. Разряд происходит по так называемой экспоненте. Так как я не люблю алгебру и матанализ, то не буду приводить различные математические выкладки. Кстати, а что такое экспонента? Ну экспонента — это график функции «е в степени икс». Короче, все учились в школе, вам лучше знать 😉
Итак, думаю стоит запомнить, что постоянная времени RC-цепи равняется произведению номиналов сопротивления и емкости и выражается в секундах, или формулой:
R — сопротивление, Ом
Для тех, кто любит считать глазами, можно построить уровень в 37% от амплитуды сигнала и затем уже аппроксимировать на ось времени. Это и будет постоянная времени RC-цепи. Как вы видите, наши алгебраические расчеты почти полностью сошлись с геометрическими, так как цена деления стороны одного квадратика по времени равняется 50 миллисекундам.
В идеальном случае конденсатор сразу же заряжается, если на него подать напряжение. Но в реальном все-таки есть некоторое сопротивление ножек, но все равно можно считать, что заряд происходит почти мгновенно. Но что будет, если заряжать конденсатор через резистор? Разбираем прошлую схему и стряпаем новую:
как только мы замыкаем ключ S, у нас конденсатор начинает заряжаться от нуля и до значения 10 Вольт, то есть до значения, которое мы выставили на блоке питания
Наблюдаем осциллограмму, снятую с конденсатора
Ничего общего не увидели с прошлой осциллограммой, где мы разряжали конденсатор на резистор? Да, все верно. Заряд тоже идет по экспоненте ;-). Так как радиодетали у нас одинаковые, то и постоянная времени тоже одинаковая. Графическим способом она высчитывается как 63% от амплитуды сигнала
Как вы видите, мы получили те же самые 100 миллисекунд.
По формуле постоянной времени RC-цепи, нетрудно догадаться, что изменение номиналов сопротивления и конденсатора повлечет за собой изменение и постоянной времени. Поэтому, чем меньше емкость и сопротивление, тем короче по времени постоянная времени. Следовательно, заряд или разряд будет происходить быстрее.
Для примера, давайте поменяем значение емкости конденсатора в меньшую сторону. Итак, у нас был конденсатора номиналом в 100 мкФ, а мы поставим 10 мкФ, резистор оставляем такого же номинала в 1 кОм. Посмотрим еще раз на графики заряда и разряда.
Вот так заряжается наш конденсатор номиналом в 10 мкФ
А вот так он разряжается
Строим на графике заряда или разряда прямую на соответствующем уровне и аппроксимируем ее на ось времени. На графике разряда будет проще 😉
Одна сторона квадратика по оси времени у нас 10 миллисекунд (чуть ниже рабочего поля написано M:10 ms), поэтому нетрудно посчитать, что постоянная времени у нас 10 миллисекунд ;-). Все элементарно и просто.
То же самое можно сказать и про сопротивление. Емкость я оставляю такой же, то есть 10 мкФ, резистор меняю с 1 кОм на 10 кОм. Смотрим, что получилось:
Вывод: чем больше номинал конденсатора и резистора, тем больше постоянная времени, и наоборот, чем меньше номиналы этих радиоэлементов, тем меньше постоянная времени. Все просто 😉
Ладно, думаю, с этим все понятно. Но куда можно применить этот принцип зарядки и разрядки конденсатора? Оказывается, применение нашлось…
Интегрирующая RC цепь
Собственно сама схема:
А что будет, если мы на нее будем подавать прямоугольный сигнал с разной частотой? В дело идет китайский генератор функций:
Выставляем на нем частоту 1 Герц и размахом в 5 Вольт
Желтая осциллограмма — это сигнал с генератора функций, который подается на вход интегрирующей цепи на клеммы Х1, Х2, а с выхода мы снимаем красную осциллограмму, то есть с клемм Х3, Х4:
Как вы могли заметить, конденсатор почти полностью успевает зарядиться и разрядиться.
Но что будет, если мы добавим частоту? Выставляю на генераторе частоту в 10 Герц. Смотрим что у нас получилось:
Конденсатор не успевает заряжаться и разряжаться как уже приходит новый прямоугольный импульс. Как мы видим, амплитуда выходного сигнала очень сильно просела, можно сказать, он скукожился ближе к нулю.
А сигнал в 100 Герц вообще не оставил ничего от сигнала, кроме малозаметных волн
Сигнал в 1 Килогерц на выходе вообще не дал ничего…
Еще бы! Попробуй-ка с такой частотой перезаряжать конденсатор 🙂
Все то же самое касается и других сигналов: синусоиды и треугольного. везде выходной сигнал почти равен нулю на частоте 1 Килогерц и выше.
«И это все, на что способна интегрирующая цепь?» — спросите вы. Конечно нет! Это было только начало.
Давайте разберемся… Почему у нас с возрастанием частоты сигнал стал прижиматься к нулю и потом вообще пропал?
Итак, во-первых, эта цепь у нас получается как делитель напряжения, и во-вторых, конденсатор — это частотно-зависимый радиоэлемент. Его сопротивление зависит от частоты. Про это можно прочитать в статье конденсатор в цепи постоянного и переменного тока. Следовательно, если бы мы подавали постоянный ток на вход (у постоянного тока частота 0 Герц), то и на выходе бы тоже получили тот же самый постоянный ток такого же значения, которое загоняли на вход. В это случае конденсатору ведь по барабану. Все что он сможет сделать в этой ситуации — тупо зарядиться по экспоненте и все. На этом его участь в цепи постоянного тока заканчивается и он стает диэлектриком для постоянного тока.
Но как только в цепь подается переменный сигнал, конденсатор вступает в игру. Тут его сопротивление уже зависит от частоты. И чем она больше, тем меньшим сопротивлением обладает конденсатор. Формула сопротивления конденсатора от частоты:
ХС — это сопротивление конденсатора, Ом
π — постоянная и равняется приблизительно 3,14
С — емкость конденсатора, Фарад
F — частота, измеряется в Герцах
С — емкость, измеряется в Фарадах
Итак, что в результате получается? А получается то, что чем больше частота, тем меньше сопротивление конденсатора. На нулевой частоте у нас сопротивление конденсатора в идеале стает равно бесконечности (поставьте в формулу 0 Герц частоту). А так как у нас получился делитель напряжения
следовательно, на меньшем сопротивлении падает меньшее напряжение. С ростом частоты сопротивление конденсатора очень сильно уменьшается и поэтому падение напряжения на нем стает почти 0 Вольт, что мы и наблюдали на осциллограмме.
Но на этом ништяки не заканчиваются.
Давайте вспомним, что из себя представляет сигнал с постоянной составляющей. Это есть ничто иное, как сумма переменного сигнала и постоянного напряжения. Взглянув на рисунок ниже, вам все станет ясно.
То есть в нашем случае можно сказать, этот сигнал (ниже на картинке) имеет в своем составе постоянную составляющую, другими словами, постоянное напряжение
Для того, чтобы выделить постоянную составляющую из этого сигнала, нам достаточно прогнать его через нашу интегрирующую цепь. Давайте рассмотрим все это на примере. С помощью нашего генератора функций мы поднимем нашу синусоиду «над полом», то есть сделаем вот так:
Итак, все как обычно, желтый входной сигнал цепи, красный — выходной. Простая двухполярная синусоида дает нам на выходе RC интегрирующей цепи 0 Вольт:
Чтобы понять, где нулевой уровень сигналов, я их пометил квадратиком:
Теперь давайте я добавлю постоянную составляющую в синусоиду, а точнее — постоянное напряжение, благо это сделать мне позволяет генератор функций:
Как вы видите, как только я поднял синус «над полом», на выходе цепи я получил постоянное напряжение величиной в 5 Вольт. Именно на 5 Вольт я поднимал сигнал в генераторе функций ;-). Цепочка выделила постоянную составляющую из синусоидального приподнятого сигнала без проблем. Чудеса!
Но мы так и не разобрались, почему цепь называется интегрирующей? Кто хорошо учился в школе, в классе эдак 8-9, то наверняка помнит геометрический смысл интеграла — это есть ничто иное, как площадь под кривой.
Давайте рассмотрим тазик с кубиками льда в двухмерной плоскости:
Что будет, если весь лед растает и превратится в воду? Все верно, вода ровным слоем покроет тазик одной плоскостью:
Но какой будет этот уровень воды? Вот именно — средний. Это среднее значение этих башен из кубиков льда. Так вот, интегрирующая цепочка делает то же самое! Тупо усредняет значение сигналов до одного постоянного уровня! Можно сказать, усредняет площадь до одного постоянного уровня.
Но самый смак получается тогда, когда мы подаем на вход прямоугольный сигнал. Давайте так и сделаем. Подадим положительный меандр на RC интегрирующую цепь.
Как вы видите, постоянная составляющая меандра равна половине его амплитуды. Думаю, вы уже и сами догадались, если бы представили тазик с кубиками льда). Или просто подсчитайте площадь каждого импульса и размажьте его равномерным слоем по осциллограмме, как гов… как сливочное масло по хлебу 😉
Ну а теперь самое веселое. Сейчас я буду менять скважность нашего прямоугольного сигнала, так как скважность — это ничто иное, как отношение периода на длительность импульса, следовательно, мы будем менять длительность импульсов.
Уменьшаю длительность импульсов
Увеличиваю длительность импульсов
Если никто ничего до сих пор не заметил, просто взгляните на уровень красной осциллограммы и все станет понятно. Вывод: управляя скважностью, мы можем менять уровень постоянной составляющей. Именно этот принцип и заложен в ШИМ (Широтно-Импульсной Модуляции). О ней как-нибудь поговорим в отдельной статье.
Дифференцирующая RC цепь
Еще одно ругательное слово, которое пришло с математики — дифференцирующий. Башка начинает сразу же болеть от одного только их произношения. Но, куда деваться? Электроника и математика неразлучные друзья.
А вот и сама дифференциальная цепочка
В схеме мы только переставили резистор и конденсатор местами
Ну а теперь проведем также все опыты, как мы делали с интегрирующей цепью. Для начала подаем на вход дифференциальной цепи низкочастотный двухполярный меандр с частотой в 1,5 Герца и с размахом в 5 Вольт. Желтый сигнал — это сигнал с генератора частоты, красный — с выхода дифференциальной цепочки:
Как вы видите, конденсатор успевает почти полностью разрядится, поэтому у нас получилась вот такая красивая осциллограмма.
Давайте увеличим частоту до 10 Герц
Как видите, конденсатор не успевает разрядиться, как уже приходит новый импульс.
Сигнал в 100 Герц сделал кривую разряда еще менее заметной.
Ну и добавим частоту до 1 Килогерца
Какой на входе, такой и на выходе 😉 С такой частотой конденсатор вообще не успевает разряжаться, поэтому вершинки выходных импульсов гладкие и ровные.
Но и на этом тоже ништяки не заканчиваются.
Давайте я подниму входной сигнал над «уровнем моря», то есть выведу его в положительную часть полностью. Смотрим, что получается на выходе (красный сигнал)
Ничего себе, красный сигнал по форме и по положению остался таким же, посмотрите — в нем нет постоянной составляющей, как в желтом сигнале, который мы подавали из нашего генератора функций.
Могу даже желтый сигнал вывести в отрицательную область, но на выходе мы все равно получим переменную составляющую сигнала без всяких хлопот:
Да и вообще пусть сигнал будет с небольшой отрицательной постоянной составляющей, все равно на выходе мы получим переменную составляющую:
Все то же самое касается и любых других сигналов:
В результате опытов мы видим, что основная функция дифференциальной цепи — это выделение переменной составляющей из сигнала, который содержит в себе как переменную, так и постоянную составляющую. Иными словами — выделение переменного тока из сигнала, который состоит из суммы переменного тока и постоянного тока.
Почему так происходит? Давайте разберемся. Рассмотрим нашу дифференциальную цепь:
Если внимательно рассмотреть эту схему, то мы можем увидеть тот же самый делитель напряжения, как и в интегрирующей цепи. Конденсатор — частотно-зависимый радиоэлемент. Итак, если подать сигнал с частотой в 0 Герц (постоянный ток), то у нас конденсатор тупо зарядится и потом вообще перестанет пропускать через себя ток. Цепь будет в обрыве. Но если мы будем подавать переменный ток, то и через конденсатор он тоже начнет проходить. Чем больше частота — тем меньше сопротивление конденсатора. Следовательно, весь переменный сигнал будет падать на резисторе, с которого мы как раз и снимаем сигнал.
Но если мы будем подавать смешанный сигнал, то есть переменный ток + постоянный ток, то на выходе мы получим просто переменный ток. В этом мы с вами уже убеждались на опыте. Почему так произошло? Да потому что конденсатор не пропускает через себя постоянный ток!
Видео «Как работает RC-цепь РЕАЛЬНО. Понятное объяснение»
Заключение
Интегрирующую цепь также называют фильтром низких частот (ФНЧ), а дифференцирующую — фильтром высоких частот (ФВЧ). Более подробно про фильтры читаем здесь. Чтобы точнее их сделать, нужно провести расчет на нужную вам частоту. RC цепи используются везде, где надо выделить постоянную составляющую (ШИМ), переменную составляющую (межкаскадное соединение усилителей), выделить фронт сигнала, сделать задержку и тд… По мере глубины погружения в электронику вы будете часто встречаться с ними.
Крутой набор радиолюбителя по ссылке алиэкспрессе.