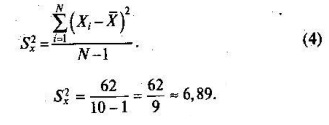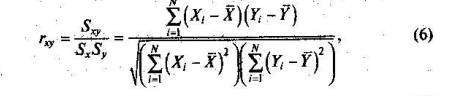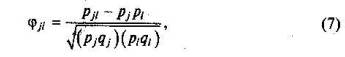Дихотомическая система оценивания что это

Дихотомическая система оценивания что это

Лекция 12. Классическая теория и методики конструирования тестов.

1. Основные этапы конструирования теста.

2. Традиционная теория тестов.

3. Математико-статистический анализ тестов и тестовых заданий.

4. Показатели связи между заданиями теста.

5. Оценка характеристик заданий теста.

1. Основные этапы конструирования теста

Перечень этапов и их очередность. Процесс создания теста, его научного обоснования, переработки и улучшения можно разбить на ряд этапов, представленных ниже.

1. Определение цели тестирования, выбор вида теста и подхода к его созданию.

2. Концептуальный выбор конструкта (переменной измерения).

3. Анализ содержания учебной дисциплины и планирование содержания теста, априорный выбор длины теста и времени его выполнения, разработка спецификации теста.

4. Определение структуры теста, форм заданий и стратегии их расположения в тесте.

5. Создание предтестовых заданий.

6. Отбор заданий в тест и их ранжирование согласно выбранной стратегии предъявления на основании априорных авторских оце­нок трудности заданий.

7. Экспертиза формы предтестовых заданий и содержания-теста.

8. Коррекция заданий и теста по результатам экспертизы.

9. Разработка методики апробационного тестирования, инст­рукций для учеников и преподавателей, проводящих апробацию

10. Формирование репрезентативной выборки апробации.

11. Проведение апробационного тестирования.

12. Проверка результатов выполнения теста (автоматизирован­ная или ручная), подготовка эмпирических данных тестирования к виду, удобному для обработки и проведения анализа.

13. Статистическая обработка результатов выполнения теста (ав­томатизированная с помощью специального программного обес­печения).

14. Анализ и интерпретация результатов обработки в целях улуч­шения качества теста. Проверка соответствия характеристик теста научно обоснованным критериям качества.

15. Коррекция содержания и формы заданий на основании дан­ных предыдущего этапа. Чистка теста и добавление новых заданий для оптимизации диапазона значений параметра трудности и улучшения системообразующих свойств заданий теста. Оптимизация длины теста и времени его выполнения на основании статисти­ческих оценок характеристик теста Оптимизация порядка распо­ложения заданий в тесте.

16. Повторение этапа апробации для выполнения очередных шагов по повышению качества теста.

17. Интерпретация данных обработки, установление норм тес­та и создание шкалы для оценки результатов испытуемых.

Апробация, анализ и коррекция теста. Апробация теста неодно­кратно повторяется. Обычно на разработку стандартизованного те­ста уходит не менее 3—4 лет, поскольку для апробации важно не только сформировать репрезентативную выборку учащихся, но и выбрать подходящее время в учебном процессе.

При разработке теста возникает своеобразный цикл, так как после его чистки создателю приходится возвращаться, к этапу ап­робация и анализа эмпирических данных тестирования, причем, как правило, не один раз,

Тщательная коррекция теста необходима особенно в тех случа­ях, когда тест должен быть стандартизован, а его результаты пла­нируется использовать для принятия административно-управлен­ческих решений в образовании.

2. Классическая (традиционная) теория тестов

Основное предположение классической теории тестов. Предпо­ложение о существовании истинного балла ( true score ) является основополагающим в классической теории тестов.

Нередко в одномерных измерениях истинный балл называют параметром учащегося, при этом предполагается, что каждому ученику можно поставить в соответствие единственное на момент измерения значение параметра, не зависящее от применяемого теста. В целом истинный балл — это идеализированная константа испытуемого в гипотетической генеральной совокупности зада­ний бесконечного теста.

Постулаты классической теории тестов. Помимо предположе­ния о существовании истинного балла в классической теории те­стов выделяют несколько постулатов, позволяющих построить ма-тематико-статистический аппарат для разработки научно обосно­ванных тестов и оценки качества результатов педагогических из­мерений [60; 81]. Эти постулаты связаны с предположениями:

— о равенстве ковариаций результатов тестирования по парал­лельным формам;

— о приближении средних значений ошибок измерения истин­ных баллов к нулю при числе тестирований, стремящемся к бес­конечности;

— о инвариантности истинных баллов относительно различных параллельных форм теста;

— о континуальном (непрерывном) распределении истинных баллов в генеральной совокупности учащихся;

— о нормальном законе распределения наблюдаемых баллов, истинных баллов и ошибок измерения.

3. Математико-статистический анализ качества тестов и тестовых заданий на основе

классической теории тестов

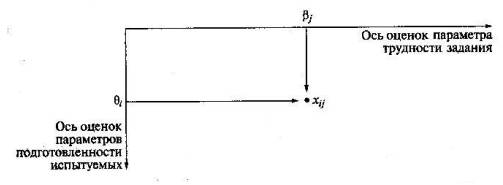
Интегрирование данных тестирования в форме матрицы удоб­но для обработки и отражает взаимодействие множеств испытуе­мых и заданий, происходящее при выполнении теста (рис. 21).

Рис.21 Геометрическая интерпретация взаимодействия множеств испытуемых и заданий теста

Правило дихотомического оценивания ответа

Матрица наблюдаемых результатов выполнения теста

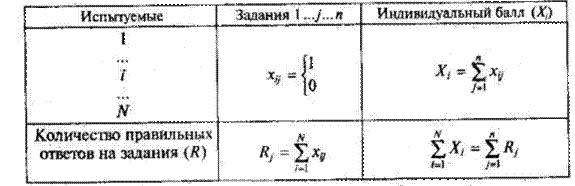
Общий вид матрицы наблюдаемых результатов выполнения N учащимися n заданий теста при дихотомических оценках по зада­ниям приведен в табл. 7.

Матрица результатов тестировании

Номер испытуемого i

После занесения результатов выполнения теста в матрицу на­чинается этап математико-статистической обработки, который включает ряд шагов. Из дидактических соображений для иллюст­рации методов обработки выбрана небольшая матрица, когда 10 учеников отвечали всего на 10 заданий теста (табл. 8). Однако все формулы и подсчеты, обсуждаемые в разделе, могут быть распро­странены на любые выборки испытуемых и применимы к тестам любой длины.

Матрица результатов с индивидуальными баллами испытуемых и количеством правильных ответов на задания теста

Третий шаг математико-статистической обработки эмпириче­ских данных тестирования. На данном этапе производится графи­ческая интерпретация распределений эмпирических данных, ко­торые можно представить в виде полигона, гистограммы или сгла­женной кривой (процентилей, огивы). Для графической интер­претации результатов учащихся необходимо их предварительное упорядочение в виде несгруппированного ряда произвольной фор­мы (табл. 11), ранжированного ряда (табл. 12), частотного распре­деления или распределения сгруппированных частот [1; 18; 59].

В табл. 11 содержатся индивидуальные баллы испытуемых, взя­тые из последнего столбца матрицы эмпирических результатов выполнения теста (см. табл. 9). В табл. 12 эти баллы располагаются в порядке возрастания слева — направо, а также приводятся места (ранги) испытуемых, соответствующие их индивидуальным бал­лам.

Упорядоченная матрица данных тестирования

Данные таблицы удобны для подведения итогов тестирования в работе педагога, поскольку в классе распределения сырых бал­лов вполне достаточно для сообщения тестовых результатов уче­никам. Например, балл 6 обеспечивает первому испытуемому ранг 5 в группе из 10 учеников. Аналогичным образом можно интер­претировать любую оценку ученика в терминах рангов. Очевидно, что равным баллам приписываются равные ранги.

Если группа учащихся велика, то для определения рангов ис­пользуют классификацию оценок по распределению частот или строят сгруппированное частотное распределение. По ряду час­тотного распределения можно получить графическое представле­ние результатов тестирования в виде полигона частот и гисто­граммы — последовательности столбцов, каждый из которых опирается на единичный (разрядный) интервал и высота которых пропорциональна частоте наблюдаемых баллов [18; 59].

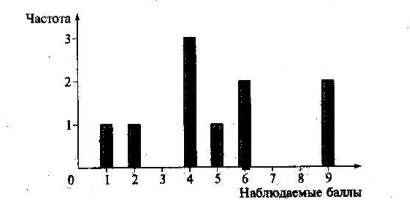
Рис. 22. Столбиковая гистограмма для распределения баллов в матрице, представленной в табл. 9

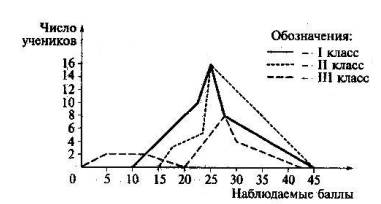
Рис. 23. Сравнение результатов тестирования

Например, матрице, представленной в табл. 10, соответствует гистограмма, приведенная на рис. 22. Середина столбца совмеща­ется с серединой интервала разряда, длина которого равна одно­му баллу.

Для сравнения двух или более распределений обычно исполь­зуют полигоны частот, так как при наложении гистограмм полу­чается довольно запутанная картина.

Например, с помощью полигонов можно сравнить результаты выполнения теста учащимися различных классов, имеющих оди­наковое количество учеников (рис. 23). На рисунке отчетливо вид­но значительное сходство в результатах тестирования у первых двух классов, имеющих довольно похожие полигоны распределе­ния оценок.

Четвертый шаг математико-статистической обработки эмпири­ческих данных тестирования. На данном этапе обработки данных оцениваются меры центральной тенденции в распределении ре­зультатов тестирования, предназначенные для выявления той точ­ки, вокруг которой в основном группируются все результаты вы­полнения теста [1; 18; 59]. При анализе результатов тестирования можно использовать разные способы определения такой централь­ной точки. Наиболее простой из них основан на выявлении моды распределения.

Мода — это такое значение, которое встречается наиболее часто среди результатов выполнения теста. Например, для дан­ных матрицы, представленной в табл. 10, модой является балл «4», потому что он встречается чаще (три раза) любого другого значения балла. Распределение может иметь одну или несколь­ко мод. В случае существования двух мод распределение называ­ется бимодальным. Если все значения баллов учеников встреча­ются одинаково часто, принято считать, что моды у распределе­ния нет.

Среднее выборочное (среднее арифметическое) определяется сумми­рованием всех значений совокупности баллов и последующим делением на их число. Для индивидуальных баллов Х_1, Х₂. X_N группы N испытуемых среднее значение X будет

Среднее арифметическое индивидуальных баллов испытуемых для рассмотренного выше примера матрицы (см. табл. 10) равно

В отличие от моды, фиксирующей одно или несколько значе­ний, на величину среднего влияют значения всех результатов рас­пределения. Таким образом, среднее арифметическое характери­зует все распределение в целом. Оно обобщает индивидуальные особенности составляющих распределения на основе уравнива­ния отдельных значений рассматриваемой величины. С другими свойствами среднего выборочного можно познакомиться в учеб­нике по статистике.

Меры центральной тенденции полезны при оценке качества теста в том случае, когда есть результаты апробации теста на ре­презентативной выборке учеников. Обычно считают, что хороший нормативно-ориентированный тест обеспечивает нормальное рас­пределение индивидуальных баллов репрезентативной выборки учеников, когда среднее значение баллов находится в центре рас­пределения, а остальные значения концентрируются вокруг сред­него по нормальному закону, т.е. примерно 70 % значений в цен­тре, а остальные сходят на нет к краям распределения, как пока­зано на рис. 24.

Рис. 24. Нормальная кривая распределения индивидуальных баллов

Если тест обеспечивает распределение баллов, близкое к нор­мальному, то это означает, что с его помощью можно определить устойчивое среднее, которое принимается в качестве одной из репрезентативных норм выполнения теста. Обратный вывод неве­рен: устойчивость тестовых норм вовсе не предполагает обязатель­ного нормального распределения эмпирических результатов вы­полнения теста. Таким образом, правильно сконструированный нормативно-ориентированный тест на репрезентативной выбор­ке учеников должен обеспечивать близкое к симметричному рас­пределение индивидуальных баллов, когда мода и среднее значе­ние примерно равны, а остальные результаты расположены во­круг среднего по нормальному закону.

Пятый шаг математико-статистической обработки эмпирических данных тестирования. На данном этапе определяются описатель­ные характеристики, служащие мерами изменчивости в распре­делении данных по гесту [1; 18; 59]. Введение мер изменчивости связано с необходимостью выявления дополнительных основа­ний для сравнения различных распределений по тестам. Если рас­пределения имеют одинаковые средние, то, оценивая и анализи­руя, меры изменчивости, можно выявить существенные отличия в качестве тестов.

Характеристика изменчивости указывает на особенности раз­броса эмпирических данных вокруг среднего значения: баллов. Отдельные значения индивидуальных баллов могут быть тесно сгруппированы вокруг своего среднего балла или, наоборот, сильно удалены от него. Для отражения характера рассеяния отдельных значений вокруг среднего используются различные меры: размах, дисперсия и стандартное отклонение.

Размах измеряет на шкале расстояние, в пределах которого изменяются все значения показателя в распределении. Напри­мер, для распределения индивидуальных баллов, представлен­ных в, табл. 10, размах равен 9-1 = 8. Вариационный размах легко вычисляется, но при характеристике распределения баллов по тесту используется крайне редко. Во-первых, размах является весьма приближенным показателем, так как не зависит от степени из­менчивости промежуточных значений, расположенных между крайними значениями в распределении баллов по тесту, Во-вторых, крайние значения индивидуальных баллов, как правило, ненадежны, поскольку содержат в себе значительную ошибку из­мерения. В этой связи более удачной мерой изменчивости считает­ся дисперсия.

Если просуммировать все отклонения, взятые со своим знаком, то для симметричных распределений сумма будет равна нулю. Чтобы отрицательные и положительные слагаемые не уничтожали друг друга, каждое отклонение возводят в квадрат, а затем находят сумму квадратов отклонений. Эта сумма будет большой, если результаты тестирования отличаются существенной неоднородностью, и малой — в случае близких результатов испытуемых по тесту. Для матрицы, представленной в табл. 9, сумма квадратов отклонений будет равна

Для рассматриваемого примера

Кроме дисперсии для характеристики меры изменчивости рас­пределения удобно использовать еще один показатель вариации, который называется стандартным отклонением и вычисляется путем извлечения квадратного корня из дисперсии:

Для рассматриваемого примера данных тестирования 6,89=2,62. Свойства дисперсии и стандартного отклонения рассматриваются подробно в учебниках по статистике. Заинтере­сованному читателю можно порекомендовать, например, книгу Дж. Гласс и Дж. Стенли «Статистические методы в педагогике и психологии» [18].

Дисперсия играет важную роль в оценке качества тестов. Низ­кая дисперсия указывает на плохое качество нормативно-ориен­тированного теста, поскольку не обеспечивается высокий диффе­ренцирующий эффект. Излишне высокая дисперсия, характерная для случая, когда все учащиеся различаются по числу выполнен­ных заданий, также требует переработки теста из-за существен­ного отличия вида распределения баллов от плакируемой нор­мальной кривой.

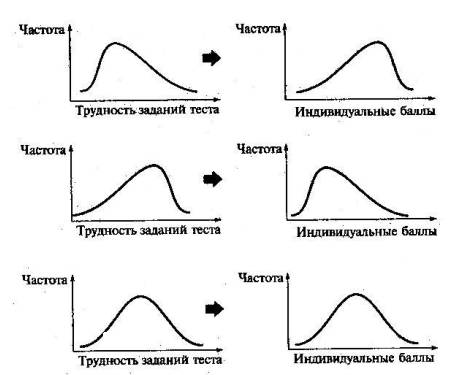
При использовании теста необходимо помнить о том, что по­лучаемое распределение индивидуальных баллов учащихся явля­ется следствием подбора трудности заданий теста, как показано на рис. 25.

.Для верхнего распределения слева характерно смещение в сто­рону легких заданий, поэтому большая часть учащихся выполнит почти все задания теста и получит высокие индивидуальные бал­лы, показанные на правом верхнем рисунке. Средние графики отражают тенденцию к приоритетному подбору самых трудных заданий при разработке теста и вытекающий отсюда всплеск у начала горизонтальной оси там, где располагаются низкие инди­видуальные баллы. Тест, представленный на нижнем графике сле­ва, обладает сбалансированной трудностью, что автоматически приводит к нормальности распределения индивидуальных баллов репрезентативной выборки учеников.

Это позволяет считать полученное распределение устойчивым по отношению к генеральной совокупности, а также помогает определить репрезентативные нормы выполнения теста.

Последующие шаги обработки данных предназначаются для оценивания мер симметрии и островершинности кривых распре­делений [1; 18; 60; 63] и выполняются обычно при разработке тестов административно-управленческого предназначения не «ру­ками», а с помощью специальных статистических пакетов для ПК.

Рис. 25. Связь распределения индивидуальных баллов и трудности зада­ний теста

4. Показатели связи между заданиями теста

Корреляция результатов учащихся по заданиям. Для итогового контроля полезно вычислять показатели связи между результата­ми учеников по отдельным заданиям теста. При этом важно по­нять, существует ли тенденция, когда одни и те же ученики до­биваются успеха в какой-либо паре заданий теста, или состав уче­ников, добивающихся успеха, полностью меняется при переходе одного задания теста к другому.

При исследовании связи между наборами данных необходимо правильно выбрать вид и форму показателя, зависящие от шкал, в которых представлены данные [18]. В частности, для оценки свя­зи между результатами выполнения учащимися двух заданий тес­та коэффициент корреляции Пирсона r _ху необходимо преобразо­вать, поскольку результаты выполнения заданий представляются в дихотомической шкале (столбцы из нулей и единиц в матрице данных по тесту). Преобразованный коэффициент Пирсона для дихотомических данных называется коэффициентом «фи» и вы­числяется по формуле

Анализ значений коэффициента корреляции р позволяет выя­вить неудачные задания теста, которые отрицательно коррелиру­ют с большинством остальных заданий и, следовательно, изме­ряют нечто иное, чем та переменная, для которой предназначал­ся тест. Отрицательные значения коэффициента корреляции ука­зывают на определенный просчет разработчиков в содержании заданий, которые рекомендуется удалить из теста. Наиболее распространенная причина появления отрицательной корреляции — отсутствие предметной чистоты содержания — встречается при разработке самых разных тестов довольно часто. Предметная чистота — скорее идеализируемое, чем реаль­ное, требование к содержанию любого теста. Так, в любом тесте по физике встречаются задания с большим количеством мате­матических преобразований, в тесте по биологии — задания, требующие, серьезных знаний по химии, в тесте по истории — за­дания, рассчитанные на выявление культурологических знаний, и т.п. Поэтому можно лишь стремиться к тому, чтобы при выпол­нении каждого задания доминировали знания по проверяемому предмету.

Для тематических тестов характерна высокая корреляция меж­ду заданиями, так как они в большинстве случаев имеют слабо варьирующее исходное содержание, что вполне объясняется на­значением теста. Однако в итоговых тестах по возможности стара­ются избегать высокой корреляции между заданиями, поскольку вряд ли имеет смысл включать в итоговый тест несколько зада­ний, оценивающих одинаковые содержательные элементы. В ито­говых тестах обычно стремятся к невысокой положительной кор­реляции, когда значения коэффициента варьируют в интервале (0; 0,3) и каждое задание вносит свой вклад в общее содержание теста.

Бисериальный коэффициент корреляции. Бисериальный коэф­фициент корреляции используется в том случае, когда один на­бор значений распределения задается в дихотомической шкале, а другой — в интервальной. Под эту ситуацию подпадает подсчет корреляции между результатами выполнения каждого задания (ди­хотомическая шкала) и суммой баллов испытуемых по заданиям теста (интервальная или квазиинтервальная шкала). С помощью подсчета значений бисериального коэффициента корреляции оце­нивается валидность, иногда называемая показателем дифферен­цирующей способности (дискриминативности) заданий теста.

Анализ значений коэффициента бисериальной корреляции, подсчитанного для оценки связи результатов по каждому заданию с суммой баллов по тесту, позволяет выявить задания с низкой валидностью, с помощью которых трудно отделить хорошо под­готовленных учащихся от слабо подготовленных учащихся тести­руемой группы. Значения, близкие к нулю, указывают на низкую дифференцирующую способность заданий теста. Если коэффици­ент бисериальной корреляции принимает отрицательные значе­ния, задание следует удалить из теста, так как при выполнении такого теста слабые ученики выполняют его верно, а сильные выбирают неверный ответ либо пропускают задание.

5. Оценка характеристик заданий теста

Оценка трудности заданий по классической теории тестов. Оценка трудности тестовых заданий в классической теорий тестов осуще­ствляется по формуле

Связь оценок трудности и валидностн заданий. Интересна взаи­мосвязь показателей трудности и валидности (дискриминативности) заданий теста. Задания с высокой дискриминативностъю обыч­но имеют среднюю трудность, поскольку именно для них харак­терен в первую очередь высокий дифференцирующий эффект. Однако обратное заключение неверно. Задания с р = 0,5 могут иметь как высокий, так и низкий дифференцирующий эффект.

При подсчете статистик по тесту всегда проводится проверка значимости полученных оценок дисперсии, асимметрии и т д. Для этого к данным, собранным по тесту, необходимо добавить информацию о принимаемом уровне риска допущения ошибки в статистическом выводе. Наиболее приемлемым для педагогичес­ких измерений является уровень в 5 %, который допускает ошиб­ку в 5 случаях из 100. После выбора степени риска проверка значимости проводится одним из описанных в литературе методов [18; 74].

Гомогенность (содержательная однородность) задания. При кон­струировании теста необходимо иметь четкое представление о со­держании заданий, которые предполагается включить в оконча­тельную версию теста. При одномерных измерениях содержание заданий должно отвечать свойству гомогенности, указывающему на степень его однородности с точки зрения оцениваемого пара­метра подготовленности ученика. Таким образом, гомогенность (однородность) — это характеристика задания, отражающая сте­пень соответствия его содержания измеряемому свойству ученика. Степень гомогенности содержания обычно оценивают с помощью факторного и корреляционного анализа.

Источник

Система оценивания знаний

Система оценивания знаний — система оценивания качества освоения образовательных программ учащимся, важнейший элемент образовательного процесса.

В мире существует множество шкал оценивания знаний. В некоторых шкалах принято использовать цифровые обозначения разрядов, причём допускаются дробные оценки, другие шкалы (например, в США) по традиции имеют дело с буквенными обозначениями. Американская шкала также имеет численную интерпретацию, при которой высшим оценкам A и A+ соответствуют 5 баллов.

Международные системы оценивания знаний

Большинство стран имеет национальную систему школьных оценок в своих школах. Также существуют и стандартные международные системы оценивания знаний.

Международный бакалавриат

В настоящее время программа GPA не существует отдельно от программы Международного бакалавриата. Системы IB Diploma и IB MYP ввели единую шкалу оценок от 1 до 7, где 7 — высшая оценка, 1 — низшая. Оценки всегда являются целыми числами.

Страны СНГ, Российская империя, СССР и РФ

В истории российского просвещения изначально, как и в Европе, существовала трёхразрядная система оценок. В списке студентов Киевской духовной академии (1737 г.) высший разряд обозначает хорошие выдающиеся успехи: «учения изрядного, надежного, доброго, честного, хорошего, похвального». Средний разряд обозначает успехи «учения посредственного, мерного, нехудого». Низший разряд характеризует успехи ниже среднего: «учения слабого, подлого, прехудого, безнадежного, ленивого».

Постепенно словесная оценка становилась однообразней и короче, она чаще заменялась цифровой, причём направление шкалы установилось противоположным германскому.

Традиция обозначать цифрами прилежание и успехи учеников утвердилась в России ещё в начале XIX века. Тогда в гимназиях употреблялись цифры от 0 до 5. Нуль показывал, что ученик совсем не исполнил своих обязанностей; если он получал два «нуля» подряд, то он подвергался телесному наказанию (до 1864 г.) «Единицу» и «двойку» ставили тогда, когда ученик неудовлетворительно приготовил урок; «тройку» ставили за посредственное прилежание; «четыре» — когда ученик хорошо исполнил свои обязанности; «пять» он получал только за отличное знание урока. Учитель был обязан ставить баллы в классе, характеризуя только знание заданного на дом урока, и не имел права учитывать внимание или рассеянность учеников во время занятия, а также временное или постоянное прилежание ученика, его возраст и способности.

В разное время в России применялись 3-, 5-, 8-, 10-, 12-балльные системы оценки знаний. Из них прижилась 5-балльная, которая и была в 1837 году официально установлена Министерством народного просвещения: «1» — слабые успехи; «2» — посредственные; «3» — достаточные; «4» — хорошие; «5» — отличные. В течение XX века оценка «1» постепенно вышла из употребления, в результате 5-балльная система трансформировалась в современную 4-балльную. В последние годы по России в некоторых учебных заведениях возвращается 5-балльная система («1» — балл за невыполненную работу). Эта традиционная для советского образования система сейчас повсеместно применяется в России и многих странах постсоветского пространства, хотя в последние годы заметен отход от неё:

Казахстан

Киргизия

Киргизия использует 5-балльную шкалу оценивания:

Республика Молдова

В Молдове в начальных классах (1-4) применяется критериальная система оценивания. За каждый продукт ребёнок самостоятельно оценивает себя по каждому критерию тремя цветами: зелёный (выполнил самостоятельно) — соответствует букве «с», жёлтый (был руководим учителем) — соответствует букве «р», красный (с постоянной поддержкой учителя) — соответствует букве «п». Суммативное оценивание выражается заглавными буквами ОХ — очень хорошо, Х — хорошо, У — удовлетворительно. В последующих классах используют 10-балльную шкалу, где 5 — минимальная удовлетворительная оценка:

Россия

Система оценки знаний в школе

С 11 января 1944 года в российских школах введена пятибалльная система оценки успеваемости учащихся согласно Постановлению Совета народных комиссаров РСФСР № 18 от 10 января 1944 года и Приказу Народного комиссара просвещения РСФСР № 24 от 10 января 1944 года.

В соответствии с инструкцией Управления начальных и средних школ Наркомпроса РСФСР, утверждённой Народным комиссаром просвещения РСФСР 29 февраля 1944 года, установлены следующие критерии оценивания учащихся:

Согласно Инструкции Управления начальных и средних школ Наркомпроса РСФСР, утверждённой Народным комиссаром просвещения РСФСР 29 февраля 1944 года, при определении четвертных и итоговых (в конце учебного года) оценок не допускается выведение их как средних арифметических. Эти итоговые оценки должны соответствовать уровню знаний учащегося к моменту его аттестации.

Эксперимент оценивания знаний учеников буквенной шкалой «ABCDF» в РФ проводился в посёлке Урдома Архангельской области (без разрешений от Министерства образования, без согласия родителей учеников) и не подтвердил свою эффективность.

Оценивание знаний учащихся начальной и средней школы исходя из процентного отношения в Российской Федерации

В течение учебного года преподаватель начальной и средней школы должен оценивать знания учащихся по таблице, приведенной ниже, и в данном случае оценки с минусом обязательны. Балл «1-» не существует в России. Если учащийся получает балл «1», то это говорит о его полном незнании пройденного материала.

При проверке работ, написанных на государственном экзамене, проверяющий преподаватель не может ставить учащемуся оценку с минусом. В этом случае таблица оценивания знаний меняется, и преподаватель должен оценивать знания учащихся по таблице, приведенной ниже.

Выставление годовых оценок в средней и начальной школе

При выставлении годовых оценок учащемуся преподаватель, исходя из четырёх четвертных, должен поставить балл, равный среднему арифметическому из итоговых оценок. Если среднее арифметическое четырёх чисел не является целым и две категории оценок стоят в равном количестве, то годовая оценка будет являться спорной и выставляется по этим данным:

1) Спорная между 5 и 4

2) Спорная между 4 и 3

2) Спорная между 3 и 2

Два семестра/ полугодия

При выставлении годовых оценок учащемуся преподаватель, исходя из двух семестровых/ полугодичных, должен поставить балл, равный среднему арифметическому из итоговых оценок двух семестров/ полугодий. Если среднее арифметическое двух чисел не является целым, то годовая оценка является спорной и выставляется по этим данным:

1) Спорная между 5 и 4

2) Спорная между 4 и 3

2) Спорная между 3 и 2

Преподаватель может выставлять годовые оценки по выше представленным данным только в том случае, если учебное пособие, по которому учащийся обучался в течение года, соответствует Федеральному Государственному образовательному стандарту (по дате на 2014 год), так как все учебники, соответствующие этому стандарту, были составлены по данному принципу:

Система оценки знаний в средних и высших учебных заведениях

В вузах и ссузах России оценки знаний установлены Приказом Государственного комитета СССР по народному образованию от 22 июня 1990 года № 432 «Об утверждении Положения о формах контроля учебной работы учащихся дневных и вечерних отделений средних специальных учебных заведений». Согласно данному нормативному документу знания, умения и навыки учащихся по всем формам контроля учебной работы, включая учебную и технологическую практики, оцениваются в баллах: 5 (Отлично); 4 (Хорошо); 3 (Удовлетворительно); 2 (Неудовлетворительно). Лабораторные работы, практические занятия и преддипломная практика оцениваются: «Зачтено», «Не зачтено». Учебные заведения культуры и искусства могут использовать другие системы оценок успеваемости учащихся, согласованные с вышестоящим органом.

Украина

Украина осенью 2000 года представила свою новую шкалу оценивания, которая заменила советскую.

Новая система оценивания базируется на основе существовавшей ранее 5-балльной шкалы оценок, которая соотносится с 12-балльной системой оценивания. Оценка 12 выставляется только за выдающиеся успехи либо за какую-либо творческую работу.

Четвёртый уровень — высокий (10-12 баллов). Знания ученика глубокие, твёрдые, системные; ученик умеет использовать их для выполнения творческих заданий, его учебная деятельность отличается умением самостоятельно оценивать разнообразные ситуации, явления и факты, проявлять и отстаивать личную позицию.

Третий уровень — достаточный (7-9 баллов). Ученик знает существенные признаки понятий, явлений, связи между ними, умеет объяснить основные закономерности, а также самостоятельно использует знания в стандартных ситуациях, владеет умственными операциями (анализом, абстрагированием, обобщением). Ответ правильный, логически обоснованный, но ученику недостает собственных суждений.

Второй уровень — средний (4-6 баллов). Ученик воспроизводит основной учебный материал, способен выполнять задания по образцу, владеет элементарными умениями учебной деятельности.

Первый уровень — начальный (1-3 балла). Ответ ученика фрагментарный, характеризуется начальными представлениями о предмете изучения.

Белоруссия

В Белоруссии используются оценки от 1 до 10.

Европа

Система оценки знаний баллами зародилась в иезуитских школах в XVI—XVII веках и имела гуманную цель заменить принятые в те времена телесные наказания на поощрения. Первая трёхбалльная шкала оценок возникла в Германии, она получилась в результате разделения всех учеников на три нумерованных разряда: лучших, средних и худших, причём переход из одного разряда в другой, более высокий, знаменовал собой приобретение целого ряда преимуществ и привилегий. Первоначально единица имела значение высшей оценки. Со временем средний разряд, к которому принадлежало наибольшее число учеников, дополнительно разделили на подразряды — так сформировалась многоуровневая ранговая шкала, с помощью которой стали оценивать познания учащихся.

Австрия

В Австрии используются оценки от 5 до 1.

Албания

В Албании используются оценки от 1 до 10. Некоторые школы разрешают использовать более высокие оценки, а также другую систему оценивания знаний.

Болгария

В Болгарии в школах используется следующая шкала оценок:

Для экзаменов и тестов для более точного результата выставляется оценка с учётом двух десятичных знаков после запятой:

Такие оценки, как, например, Хорошо (3,50) или Превосходно (5,75) являются общими. Любая оценка, равная либо большая 50, считается удовлетворительной. Минимальной является оценка 2,00; оценки ниже 3,00 являются неудовлетворительными, и максимальной является оценка 6,00. Оценки наподобие Очень хорошо (5-) и Средне (3+) также возможны, но они не учитываются в подсчётах.

Грубо говоря, болгарская шкала может приравниваться к американской следующим образом: 6=A, 5=B, 4=C, 3=D и 2=F. Также её можно сравнить с австралийской шкалой оценивания: 6=HD, 5=D, 4=Cr, 3=P и 2=F.

Наиболее распространённая формула подсчёта оценок в болгарских школах в настоящее время следующая: итоговая оценка = (6 * число правильных ответов) / общее число вопросов. Таким образом, если учащийся ответил правильно на 7 вопросов из 10, его оценка будет следующей: (6*7)/10 = 4,20, которая оценивается как Хорошо (4), что соответствует среднему уровню знаний.

Босния и Герцеговина

В Боснии и Герцеговине в начальных и средних школах используются оценки от 5 до 1, в университетах используется шкала оценивания от 10 до 5.

В начальных и средних школах используется следующая шкала:

Шкала оценивания в университетах:

Венгрия

С 1950 года в Венгрии используется 5-балльная шкала оценивания. В ней присутствует всего одна неудовлетворительная оценка: 1 — elégtelen (Неудовлетворительно). В целом, нижний предел шкалы варьируется от 50 % до 60 % или на один балл выше. Также в этой шкале присутствуют следующие оценки: 2 — elégséges (Удовлетворительно или Достаточно), 3 — közepes (Средне), 4 — jó (Хорошо) и 5 — jeles (Превосходно).

Пятибалльная система оценивания в большинстве случаев используется в конце семестра, а также на других образовательных уровнях (например, в начальной школе, старшей школе, университете). Во время учебного года учитель имеет право использовать шкалу оценок, применяемую в начальной школе. Также после оценки может использоваться знак (,) («alá»), а также апостроф (’) («fölé»). Существуют и промежуточные оценки (например, 3/4) («háromnegyed»), что является эквивалентом оценки 3,5; 4/5 — оценка между 4 и 5 и т. д. Иногда, для того чтобы показать, что за семестр у обучающегося произошёл большой прогресс, может использоваться и оценка «5*» («csillagos ötös»).

Германия

В Германии в среднем образовании используется 6-балльная система оценок с обратной зависимостью, которая имеет следующие количественные и качественные обозначения:

В некоторых учебных заведениях для выведения средней оценки используется пересчёт приведённых выше оценок в баллы по следующему соотношению: оценка 1 = 15 баллов, 2 = 12 баллов, 3 = 9 баллов, 4 = 6 баллов, 5 = 3 балла и оценка 6 = 0 баллов.

В высшем образовании используется 5-балльная система оценок, пять количественных и качественных параметров которой полностью идентичны приведённым выше пяти первым параметрам 6-балльной системы оценок среднего образования.

Дания

В Дании в 2007 году была принята 7-балльная система оценивания (syv-trins-skalaen), которая стала заменой старой 13-балльной системы оценивания (13-skala). Новая шкала была создана и совмещена в соответствии со стандартами ECTS-шкалы. Syv-trins-skalaen состоит из семи различных оценок в диапазоне от 12 до −3, с максимальной оценкой в 12 баллов. Эта новая шкала является остатком «чистой» шкалы, а это означает, что оценка не всегда соответствует заслугам.

Исландия

В Исландии используются оценки от 0 до 10, где 5 является наименьшей удовлетворительной оценкой, однако в некоторых случаях наименьшей удовлетворительной оценкой является 3,5.

Литва и Латвия

В Литве и Латвии используются баллы от 1 до 10. Наименьшей удовлетворительной оценкой является 4. В большинстве случаев ученику нельзя исправлять оценки от 5 баллов до 10, однако бывают школы, где ученики имеют возможность исправить эти оценки. Баллы от 1 до 4 являются неудовлетворительными и должны быть исправлены. Ученик не может перейти в следующий класс, если имеет в табеле оценки ниже 4 баллов.

Северная Македония

Шкала для начальных и средних школ:

Норвегия

В начальной школе (Barneskole, в возрасте от 6 до 13 лет) официально оценки не ставятся. Конечно, преподаватели пишут собственные комментарии или анализы тестов в конце каждой четверти. В младших и старших классах средней школы используется шкала от 1 до 6, где 6 — высшая оценка, а 2 — самая низкая удовлетворительная оценка. Для обычных тестов и четвертных результатов оценки часто употребляются со знаками «+» и «−» (кроме 6+ и 1−). Также в общей практике используются такие оценки, как 5/6 или 4/3, что указывает на результат между этими двумя оценками. Конечно, те оценки, которые учащиеся получают в свой диплом (Vitnemål), содержат целое число: 1, 2, 3, 4, 5 или 6. Нецелочисленный средний балл учащегося также указывается в дипломе Vitnemål.

В высшем образовании в соответствии с системой ECTS оценки за университетские и аспирантские экзамены выставляются по шкале от A (высший балл) до F (низший балл), где E является минимальным проходным баллом. Система ECTS была введена в университетах и колледжах Норвегии в начале 2000-х годов, в школах оценки переводятся в систему ECTS с 2003 года. До 2003 года наиболее распространённой шкалой оценок, используемой на университетском уровне, была шкала 1,0 (высший балл) до 6,0 (низший балл) с минимальным удовлетворительным результатом в 4,0.

Румыния

В начальных школах Румынии используется следующая шкала:

В средних и старших школах и академических институтах используется 10-балльная шкала, где 5 — наименьшая удовлетворительная оценка:

В этой системе нет оценки 0, а 1 ставится только за списывание. Если учащийся выполнил 86 % заданий, то он будет иметь результат в 8,60 балла, который будет округлён до 9.

Сербия

В Сербии имеется такая же шкала оценивания, что и в бывшей Югославии. В начальных и средних школах используется 5-балльная шкала:

Чехия

В Чехии 5-балльная шкала используется в начальных и средних школах:

Турция

В Турции применяется шкала оценивания от 1 до 5.

Финляндия

Школьная шкала оценок в Финляндии формально имеет диапазон от 0 до 10, но оценки ниже 4 не ставятся. Таким образом, в настоящее время шкала оценок делится на неудовлетворительные (4) и оценки от 5 до 10, являющиеся удовлетворительными. Данная шкала оценивания похожа на румынскую шкалу:

Источник