Дискретная математика что это простыми словами

Что такое дискретность (дискретная математика, сигнал, величины, видеокарты, а так же дискретность в биологии)

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Знать все обо всем попросту невозможно. Человек на протяжении всей жизни стремится познать себя и окружающую его действительность.

Вот и сегодня мы продолжим свой познавательный процесс, поговорим о новом (для многих) термине – « дискретность», и о сферах, где он применяется.

Дискретность – это …

Наш мир непрерывен, мы живем в постоянно меняющемся времени и пространстве. Наша жизнь тоже непрерывна до своего конечного момента. Согласитесь, невозможно сейчас жить, через час не жить, а потом вновь возродиться.

В противопоставлении непрерывности существует дискретность. В переводе с «вечно живого» латинского языка «дискретность» (discretus) обозначает прерывность, разделенность.

Дискре́тность (от лат. discretus — разделённый, прерывистый) — свойство, противопоставляемое непрерывности, прерывистость. Синонимы к слову дискретный: корпускулярный, отдельный, прерывистый, раздельный и т. п.

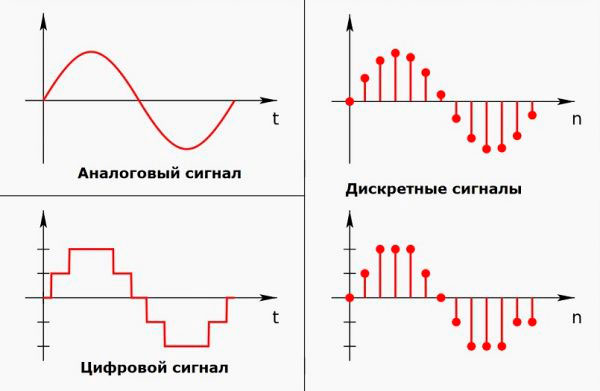
Например, линия непрерывна (на определенном промежутке), пунктир – прерывистая линия. Поэтому пунктир можно назвать дискретной линией. Проиллюстрирую понятие дискретности:

Дискретность можно толковать следующим образом:

Далее проанализируем особенности применения термина в различных областях.

Дискретная математика

Если коротко и простыми словами, то дискретная математика (ДМ)– это наука, которые изучает математические объекты, принимающие отдельные (дискретные) значения.

ДМ условно подразделяется на пять направлений:

Дискретная величина

Дискретность какой-либо величины подразумевает, что ее значения можно пронумеровать, измерить и посчитать.

Такими величинами оперирует, например, экономика. Различные экономические показатели фиксируют и рассчитывают с определенной периодичностью (например, раз в месяц, квартал, полугодие и т.д.). Таким образом, изменение показателей происходит не непрерывно во времени, а как бы «скачками» через установленные интервалы времени.

Дискретность в информатике

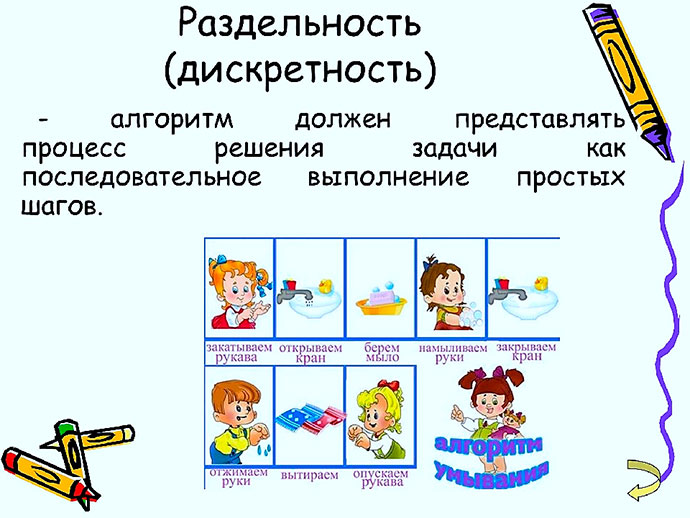
Программирование – это создание программ с использованием различных алгоритмов и языков программирования. Алгоритмы являются дискретными объектами, потому как представляют собой четкое последовательное выполнение ранее разработанных упрощенных шагов-действий (подпрограмм).

Только исполнение шага № 1 дает возможность выполнить шаг № 2 и т.д. Таким образом, этот процесс дискретен.

Как пример – алгоритм умывания (компьютерные программы создаются по тому же принципу):

Дискретная видеокарта

Видеокарта – один из важнейших элементов компьютера, отвечающий за визуализацию информации. Конструкция компа может быть оснащена либо интегрированной (встроенной) видеокартой, либо дискретной. Встроенная размещается в процессоре или на материнской плате, т.е. она неотделима от конкретного компьютера.

Дискретная видеокарта выполнена на отдельной плате, снабжена индивидуальным графическим процессором и памятью. Поэтому она более производительна, чем интегрированная.

Часто в компьютерах применяются видеокарты обоих видов, что позволяет пользователю при необходимости переключаться с одной на другую.

Дискретность в биологии

Все биологические объекты состоят из отдельных (дискретных) «кирпичиков», которые в совокупности образуют единый организм. Например, скелет человека состоит из костей, кости –из костной ткани, она, в свою очередь – из клеток.

Автор статьи: Елена Копейкина

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Благодарю за дискретное изложение материала

Источник

Основы дискретной математики

Привет, хабр. В преддверии старта базового курса «Математика для Data Science» делимся с вами переводом еще одного полезного материала.

Об этой статье

Эта статья содержит лишь малую часть информации по заявленной теме. Рассматривайте ее как вводный курс перед началом всестороннего изучения предмета. Надеюсь, вы найдете в ней полезную информацию. Знание дискретной математики помогает описывать объекты и задачи в информатике, особенно когда дело касается алгоритмов, языков программирования, баз данных и криптографии. В дальнейшем я планирую подробнее раскрыть темы, затронутые в этой статье. Приятного чтения!

ЧТО ТАКОЕ ДИСКРЕТНАЯ МАТЕМАТИКА?

Это область математики, изучающая объекты, которые могут принимать только уникальные отдельные значения.

Мы рассмотрим пять основных разделов в следующем порядке.

ЛОГИКА

Что такое логика?

Это наука о корректных рассуждениях. Мы будем использовать приемы идеализации и формализации. Неформальная логика изучает использование аргументов в естественном языке.

Формальная логика анализирует выводы с чисто формальным содержанием. Примерами формальной логики являются символическая логика и силлогистическая логика (о которой писал Аристотель).

Начнем с азов. Рассмотрим следующее высказывание на естественном языке:

«Если я голоден, я ем».

Пусть «голоден» будет посылкой A, а «ем» — следствием B. Попробуем формализовать:

A => B (то есть из A следует B)

NB. Посылка и следствие являются суждениями.

Логические выражения

Для нас важна форма, а НЕ содержание. Значение будет истинным, если оно соответствует форме.

Например, 10 4 — ИСТИНА.

Логические операции

Суждение P — это утверждение, которое может быть как истинным, так и ложным.

Обозначим истинное значение P единицей (1), а ложное значение P нулем (0).

Существует другое суждение; обозначим истинное значение Q единицей (1), а ложное значение Q нулем (0).

Рассмотрим логические операции с суждениями, значение которых истинно. Они могут сами образовывать истинные значения путем выполнения соответствующих операций над истинными значениями.

Источник

Дискретная математика

Дискре́тная матема́тика — область математики, занимающаяся изучением дискретных структур, которые возникают как в пределах самой математики, так и в её приложениях.

К числу таких структур могут быть отнесены конечные группы, конечные графы, а также некоторые математические модели преобразователей информации, конечные автоматы, машины Тьюринга и так далее. Это примеры структур конечного (финитного) характера. Раздел дискретной математики, изучающий их, называется конечной математикой. Иногда само это понятие расширяют до дискретной математики. Помимо указанных конечных структур, дискретная математика изучает некоторые алгебраические системы, бесконечные графы, вычислительные схемы определённого вида, клеточные автоматы и т. д. В качестве синонима иногда употребляется термин «дискретный анализ».

Содержание

Разделы дискретной математики

Примечания

Литература

См. также

Ссылки

Полезное

Смотреть что такое «Дискретная математика» в других словарях:

ДИСКРЕТНАЯ МАТЕМАТИКА — то же, что конечная математика … Большой Энциклопедический словарь

дискретная математика — то же, что конечная математика. * * * ДИСКРЕТНАЯ МАТЕМАТИКА ДИСКРЕТНАЯ МАТЕМАТИКА, то же, что конечная математика (см. КОНЕЧНАЯ МАТЕМАТИКА) … Энциклопедический словарь

ДИСКРЕТНАЯ МАТЕМАТИКА — конечная математика, раздел математики, занимающийся изучением св в объектов конечного характера. К их числу могут быть отнесены, напр., конечные группы, конечные графы, нек рые матем. модели преобразователей информации. Д. м. теоретич. основа… … Большой энциклопедический политехнический словарь

ДИСКРЕТНАЯ МАТЕМАТИКА — то же, что конец ноя математика … Естествознание. Энциклопедический словарь

«Дискретная математика» — научный журнал РАН, с 1989, Москва. Учредитель (1998) Отделение математики РАН. 4 номера в год … Энциклопедический словарь

Теория функциональных систем (дискретная математика) — У этого термина существуют и другие значения, см. Теория функциональных систем (значения). Теория функциональных систем раздел дискретной математики, занимающийся изучением функций, описывающих работу дискретных преобразователей. В теории… … Википедия

МАТЕМАТИКА — (греч. mathematike от mathema наука), наука, в которой изучаются пространственные формы и количественные отношения. До нач. 17 в. математика преимущественно наука о числах, скалярных величинах и сравнительно простых геометрических фигурах;… … Большой Энциклопедический словарь

Математика — Евклид. Деталь «Афинской школы» Рафаэля Математика (от др. греч … Википедия

математика — и; ж. [греч. mathēmatikē] 1. Наука о количественных отношениях и пространственных формах действительного мира. Высшая м. Элементарная м. Прикладная м. Законы математики. // Учебный предмет, изучающий эту науку. Экзамен по математике. Преподавать… … Энциклопедический словарь

Математика гармонии — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/22 ноября 2012. Пока процесс обсуждени … Википедия

Источник

Дискретная математика

В контексте математики в целом дискретная математика часто отождествляется с конечной математикой — направлением, изучающим конечные структуры — конечные графы, конечные группы, конечные автоматы. И при этом можно выделить некоторые особенности, не присущие разделам, работающим с бесконечными и непрерывными структурами. Так, в дискретных направлениях как правило обширнее класс разрешимых задач, так как во многих случаях возможен полный перебор вариантов, тогда как в разделах, имеющих дело с бесконечными и непрерывными структурами, для разрешимости обычно требуются существенные ограничения на условия. В этой же связи в дискретной математике особо важную роль играют задачи построения конкретных алгоритмов, и в том числе, эффективных с точки зрения вычислительной сложности. Ещё одна особенность дискретной математики — невозможность применения для её экстремальных задач техник анализа, существенно использующих недоступные для дискретных структур понятия гладкости. В широком смысле, дискретной математикой могут считаться охваченными значительные части алгебры, теории чисел, математической логики.

В рамках учебных программ дискретная математика обычно рассматривается как совокупность разделов, связанных с приложениями к информатике и вычислительной технике: теория функциональных систем, теория графов, теория автоматов, теория кодирования, комбинаторика, целочисленное программирование.

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

Данная статья представляет собой обзор основных событий и тенденций в истории математики с древнейших времён до наших дней.

Источник

Дискретная математика: для чего они нужны, теория множеств

Содержание:

В дискретная математика Они соответствуют той области математики, которая отвечает за изучение набора натуральных чисел; то есть набор счетных конечных и бесконечных чисел, в котором элементы можно пересчитывать отдельно, один за другим.

Эти наборы известны как дискретные наборы; Примером этих наборов являются целые числа, графики или логические выражения, и они применяются в различных областях науки, в основном в информатике или вычислениях.

Описание

В дискретной математике процессы счетные, в их основе лежат целые числа. Это означает, что десятичные числа не используются и, следовательно, приближения или пределы не используются, как в других областях. Например, неизвестное значение может быть равно 5 или 6, но не 4,99 или 5,9.

С другой стороны, в графическом представлении переменные будут дискретными и даны из конечного набора точек, которые подсчитываются одна за другой, как показано на изображении:

Дискретная математика возникает из-за необходимости получить точное исследование, которое можно объединить и проверить, чтобы применить его в разных областях.

Для чего нужна дискретная математика?

Дискретная математика используется во многих областях. Среди основных можно выделить следующие:

Комбинаторный

Изучите конечные наборы, в которых элементы можно упорядочивать, комбинировать и подсчитывать.

Теория дискретного распределения

Изучите события, которые происходят в пространствах, где выборки могут быть счетными, в которых непрерывные распределения используются для аппроксимации дискретных распределений, или наоборот.

Теория информации

Это относится к кодированию информации, используемой для разработки, передачи и хранения данных, таких как аналоговые сигналы.

Вычисление

С помощью дискретной математики задачи решаются с использованием алгоритмов, а также того, что можно вычислить, и времени, которое требуется для этого (сложность).

Важность дискретной математики в этой области возросла в последние десятилетия, особенно для развития языков программирования и программирования. программное обеспечение.

Криптография

Он полагается на дискретную математику для создания структур безопасности или методов шифрования. Примером этого приложения являются пароли, отправляющие биты, содержащие информацию, отдельно.

Благодаря изучению свойств целых и простых чисел (теория чисел) эти методы безопасности могут быть созданы или уничтожены.

Логика

Для доказательства теорем или, например, проверки программного обеспечения используются дискретные структуры, которые обычно образуют конечное множество.

Теория графов

Он позволяет решать логические проблемы, используя узлы и линии, которые образуют тип графа, как показано на следующем изображении:

Это область, тесно связанная с дискретной математикой, потому что алгебраические выражения дискретны. Благодаря этому разрабатываются электронные схемы, процессоры, программирование (булева алгебра) и базы данных (реляционная алгебра).

Геометрия

Изучите комбинаторные свойства геометрических объектов, например плоского покрытия. С другой стороны, вычислительная геометрия позволяет разрабатывать геометрические задачи, применяя алгоритмы.

Теория множеств

В дискретной математике множества (конечные и бесконечные счетные) являются основной целью исследования. Теория множеств была опубликована Джорджем Кантором, который показал, что все бесконечные множества имеют одинаковый размер.

В математике существуют различные наборы, которые группируют определенные числа в соответствии с их характеристиками. Так, например, имеем:

Наборы именуются прописными буквами алфавита; а элементы названы строчными буквами в фигурных скобках (<>) и разделены запятыми (,). Обычно они представлены в виде диаграмм Венна и Кэролла, а также в виде вычислений.

С помощью основных операций, таких как объединение, пересечение, дополнение, различие и декартово произведение, наборы и их элементы управляются на основе отношения принадлежности.

Существует несколько классов множеств, наиболее изученными в дискретной математике являются следующие:

Конечный набор

Он состоит из конечного числа элементов и соответствует натуральному числу. Так, например, A = <1, 2, 3,4>— это конечное множество, состоящее из 4 элементов.

Бесконечный набор учетных записей

Это тот, в котором существует соответствие между элементами множества и натуральными числами; то есть из одного элемента могут быть последовательно перечислены все элементы набора.

Таким образом, каждый элемент будет соответствовать каждому элементу набора натуральных чисел. Например:

Это метод, используемый для решения непрерывных задач (моделей и уравнений), которые необходимо преобразовать в дискретные задачи, в которых решение известно с приближением решения непрерывной задачи.

С другой стороны, дискретизация пытается извлечь конечную величину из бесконечного множества точек; Таким образом, непрерывная единица превращается в отдельные единицы.

Обычно этот метод используется в численном анализе, например, при решении дифференциального уравнения, с помощью функции, которая представлена ​​конечным количеством данных в своей области, даже если она является непрерывной.

Ссылки

Что происходит в вашем мозгу, когда вы едите шоколад или какао?

3 закона Менделя и горох: вот чему они нас учат

Источник