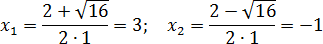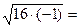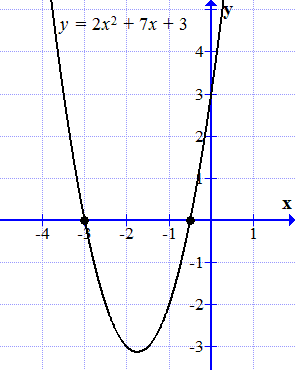Дискриминант отрицательный что значит
Дискриминант
Дискриминантом квадратного трехчлена называют выражение \(b^<2>-4ac\), где \(a, b\) и \(c\) – коэффициенты данного трехчлена.
Например, для трехчлена \(3x^2+2x-7\), дискриминант будет равен \(2^2-4\cdot3\cdot(-7)=4+84=88\). А для трехчлена \(x^2-5x+11\), он будет равен \((-5)^2-4\cdot1\cdot11=25-44=-19\).
Дискриминант и корни квадратного уравнения
Значение дискриминанта показывает количество корней квадратного уравнения:
— если \(D\) положителен – уравнение будет иметь два корня;
— если \(D\) равен нулю – только один корень;
— если \(D\) отрицателен – корней нет.
Если дискриминант положителен
В этом случае корень из него – это некоторое положительное число, а значит \(x_<1>\) и \(x_<2>\) будут различны по значению, ведь в первой формуле \(\sqrt
Пример: Найдите корни уравнения \(x^2+2x-3=0\)
Решение:
Вычисляем дискриминант по формуле \(D=b^2-4ac\)
Найдем корни уравнения
Получили два различных корня из-за разных знаков перед \(\sqrt
Если дискриминант равен нулю
А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.
То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.
Пример: Найдите корни уравнения \(x^2-4x+4=0\)
Решение:
Вычисляем дискриминант по формуле \(D=b^2-4ac\)
Находим корни уравнения
Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.
Если дискриминант отрицателен
В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.
Пример: Найдите корни уравнения \(x^2+x+3=0\)
Решение
Вычисляем дискриминант по формуле \(D=b^2-4ac\)
Находим корни уравнения
Оба корня содержат невычислимое выражение \(\sqrt<-11>\), значит, и сами не вычислимы
То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение \(x^2+x+3\) получился ноль.
Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.
Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!
Дискриминант
квадратного уравнения
Мы уже разобрали, как решать квадратные уравнения. Теперь давайте более подробно рассмотрим, что называют дискриминантом квадратного уравнения.
Вернемся к нашей формуле для нахожденя корней квадратного уравнения.
Выражение « b 2 − 4ac », которое находится под корнем, принято называть дискриминантом и обозначать буквой « D ».
По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:
По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».
В зависимости от знака « D » (дискриминанта) квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.
I случай
D > 0
(дискриминант больше нуля)
x1;2 =
| −b ± √ D |
| 2a |
x1;2 =
| −5 ± √ 81 |
| 2 · 2 |
x1;2 =
| −5 ± 9 |
| 4 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 1 | x2 = −3
| ||||
| x1 = 1 | x2 = −3
|
Ответ: x1 = 1; x2 = −3
| 1 |
| 2 |
II случай
D = 0
(дискриминант равен нулю)
D = b 2 − 4ac
D = (−8) 2 − 4 · 16 · 1
D = 64 − 64
D = 0
x1;2 =
| −b ± √ D |
| 2a |
x1;2 =
| − (−8) ± √ 0 |
| 32 |
x1;2 =
| 8 ± 0 |
| 32 |
x =
| 8 |
| 32 |
x =
| 1 |
| 4 |
Ответ: x =
| 1 |
| 4 |
III случай
D
(дискриминант меньше нуля)
D = b 2 − 4ac
D = (−6) 2 − 4 · 9 · 2
D = 36 − 72
D = −36
D
x1;2 =
| −b ± √ D |
| 2a |
x1;2 =
| − (−6) ± √ −36 |
| 32 |
Ответ: нет действительных корней
Решение квадратных уравнений
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.
Дискриминант
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
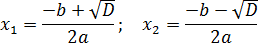
Первое уравнение:
x 2 − 2 x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2 x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
Наконец, третье уравнение:
x 2 + 12 x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид a x 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
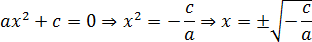
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (− c / a ) ≥ 0. Вывод:
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
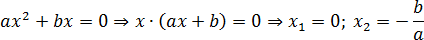
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
x 2 − 7 x = 0 ⇒ x · ( x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5 x 2 + 30 = 0 ⇒ 5 x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4 x 2 − 9 = 0 ⇒ 4 x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Если в дискриминанте отрицательное число
Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:
Пример 42.4. Решить уравнение: 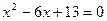
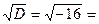
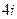
Тогда 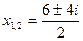
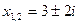
Ответ:
Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.
Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение п-й степени имеет п комплексных корней (при этом некоторые корни являются кратными). Эти результаты подчеркивают ту исключительную роль, которую играют комплексные числа в теории алгебраических уравнений.
Дата добавления: 2014-12-27 ; Просмотров: 11818 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Как решать квадратные уравнения?
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю. Тогда у вас одно решение. Строго говоря, это не один корень, а два одинаковых.
Например, для трехчлена (3x^2+2x-7), дискриминант будет равен (2^2-4cdot3cdot(-7)=4+84=88). А для трехчлена (x^2-5x+11), он будет равен ((-5)^2-4cdot1cdot11=25-44=-19).
Дискриминант и корни квадратного уравнения
Значение дискриминанта показывает количество корней квадратного уравнения:
– если (D) положителен – уравнение будет иметь два корня;
– если (D) равен нулю – только один корень;
– если (D) отрицателен – корней нет.
Если дискриминант положителен
В этом случае корень из него – это некоторое положительное число, а значит (x_ ) и (x_ ) будут различны по значению, ведь в первой формуле (sqrt ) прибавляется, а во второй – вычитается. И мы имеем два разных корня.
Пример: Найдите корни уравнения (x^2+2x-3=0)
Решение:
Вычисляем дискриминант по формуле (D=b^2-4ac)
Найдем корни уравнения
Получили два различных корня из-за разных знаков перед (sqrt )
На графике квадратичной функции положительный дискриминант будет означать пересечение функции с осью икс ровно в двух точках – корнях уравнения. И это логично. Вдумайтесь – если уравнение (x^2+2x-3=0) имеет корни (x_ =1) и (x_ =-3), значит при подстановке (1) и (-3) вместо икса, левая часть станет нулем. А значит, если те же самые единицу и минус тройку подставить в функцию (y=x^2+2x-3) получим (y=0). То есть, функция (y=x^2+2x-3) проходит через точки ((1;0)) и ((-3;0)) (подробнее смотри статью Как построить график функции ).
Если дискриминант равен нулю
А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.
То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.
Пример: Найдите корни уравнения (x^2-4x+4=0)
Решение:
Вычисляем дискриминант по формуле (D=b^2-4ac)
Находим корни уравнения
Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.
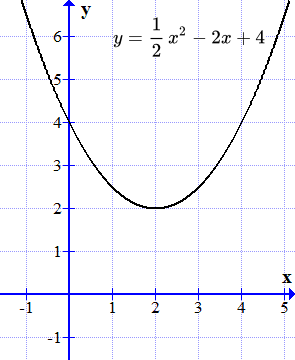
На графике квадратичной функции нулевой дискриминант означает одну точку пересечения функции с осью икс. Все аналогично изложенному выше: два корня – две точки пересечения, один корень – одна. В частности, функция (y=x^2-4x+4) будет выглядеть вот так:
Если дискриминант отрицателен
В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.
Пример: Найдите корни уравнения (x^2+x+3=0)
Решение
Вычисляем дискриминант по формуле (D=b^2-4ac)
Находим корни уравнения
Оба корня содержат невычислимое выражение (sqrt ), значит, и сами не вычислимы
То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение (x^2+x+3) получился ноль.
Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.
Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!
Если дискриминант отрицательный то сколько корней
Например, для трехчлена (3x^2+2x-7), дискриминант будет равен (2^2-4cdot3cdot(-7)=4+84=88). А для трехчлена (x^2-5x+11), он будет равен ((-5)^2-4cdot1cdot11=25-44=-19).
Дискриминант и корни квадратного уравнения
Значение дискриминанта показывает количество корней квадратного уравнения:
– если (D) положителен – уравнение будет иметь два корня;
– если (D) равен нулю – только один корень;
– если (D) отрицателен – корней нет.
Если дискриминант положителен
В этом случае корень из него – это некоторое положительное число, а значит (x_ ) и (x_ ) будут различны по значению, ведь в первой формуле (sqrt ) прибавляется, а во второй – вычитается. И мы имеем два разных корня.
Пример: Найдите корни уравнения (x^2+2x-3=0)
Решение:
Вычисляем дискриминант по формуле (D=b^2-4ac)
Найдем корни уравнения
Получили два различных корня из-за разных знаков перед (sqrt )
На графике квадратичной функции положительный дискриминант будет означать пересечение функции с осью икс ровно в двух точках – корнях уравнения. И это логично. Вдумайтесь – если уравнение (x^2+2x-3=0) имеет корни (x_ =1) и (x_ =-3), значит при подстановке (1) и (-3) вместо икса, левая часть станет нулем. А значит, если те же самые единицу и минус тройку подставить в функцию (y=x^2+2x-3) получим (y=0). То есть, функция (y=x^2+2x-3) проходит через точки ((1;0)) и ((-3;0)) (подробнее смотри статью Как построить график функции ).
Если дискриминант равен нулю
А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.
То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.
Пример: Найдите корни уравнения (x^2-4x+4=0)
Решение:
Вычисляем дискриминант по формуле (D=b^2-4ac)
Находим корни уравнения
Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.
На графике квадратичной функции нулевой дискриминант означает одну точку пересечения функции с осью икс. Все аналогично изложенному выше: два корня – две точки пересечения, один корень – одна. В частности, функция (y=x^2-4x+4) будет выглядеть вот так:
Если дискриминант отрицателен
В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.
Пример: Найдите корни уравнения (x^2+x+3=0)
Решение
Вычисляем дискриминант по формуле (D=b^2-4ac)
Находим корни уравнения
Оба корня содержат невычислимое выражение (sqrt ), значит, и сами не вычислимы
То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение (x^2+x+3) получился ноль.
Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.
Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!
Как решать квадратные уравнения?
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю. Тогда у вас одно решение. Строго говоря, это не один корень, а два одинаковых.
Основные формулы
Графическая интерпретация
Ниже приводятся примеры таких графиков.
Полезные формулы, связанные с квадратным уравнением
Вывод формулы для корней квадратного уравнения
Выполняем преобразования и применяем формулы (f.1) и (f.3):
Итак, мы получили формулу для многочлена второй степени в виде:
.
Отсюда видно, что уравнение
Примеры определения корней квадратного уравнения
Пример 1
Отсюда получаем разложение квадратного трехчлена на множители:
График функции y = 2 x 2 + 7 x + 3 пересекает ось абсцисс в двух точках.
Пример 2
Тогда разложение трехчлена на множители имеет вид:
.
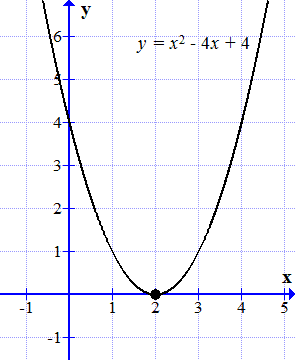
График функции y = x 2 – 4 x + 4 касается оси абсцисс в одной точке.
Построим график функции
.
График этой функции является параболой. Она касается оси абсцисс (ось ) в одной точке:
.
Эта точка является корнем исходного уравнения (2.1). Поскольку этот корень входит в разложение на множители два раза:
,
то такой корень принято называть кратным. То есть считают, что имеется два равных корня:
.
Пример 3
Можно найти комплексные корни:
;
;
.
График функции не пересекает ось абсцисс. Действительных корней нет.
Построим график функции
.
График этой функции является параболой. Она не пересекает ось абсцисс (ось ). Поэтому действительных корней нет.
Действительных корней нет. Корни комплексные:
;
;
.