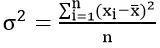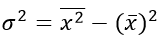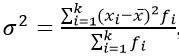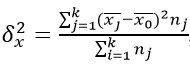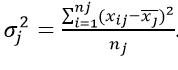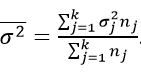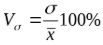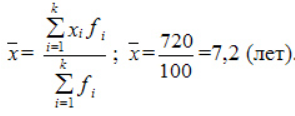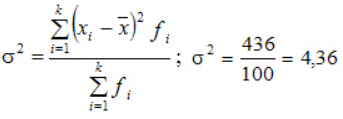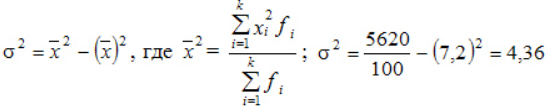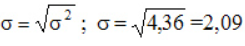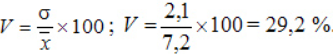Дисперсия что это простыми словами

Значение слова «дисперсия»

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Дисперсия волн — в физике зависимость фазовой скорости волны от её частоты, различают:

Закон дисперсии — в физике закон, выражающий зависимость фазовой скорости волны от её частоты.

Дисперсия случайной величины — одна из усреднённых характеристик случайной величины.

Дисперсия (химия) — образования из двух или более фаз (тел), которые совершенно или практически не смешиваются и не реагируют друг с другом химически

Дисперсия (биология) — термин, обозначающий разнообразие признаков в популяции.

Дисперсия второй вязкости

ДИСПЕ’РСИЯ, и, мн. нет, ж. [латин. dispersio]. 1. Расхождение световых лучей разного цвета при прохождении сквозь преломляющую среду (опт.). 2. Состояние большего или меньшего раздробления вещества (ест.).

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

диспе́рсия

1. матем. стат. разброс чего-либо и численная характеристика такого разброса ◆ Этот старый дурак не сообразил, что существует дисперсия свойств… Стругацкие, «Понедельник начинается в субботу», 1964 г. (цитата из НКРЯ) ◆ В теории вероятностей — дисперсия случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания Владимир Горбачёв, «Концепции современного естествознания», 2003 г. (цитата из НКРЯ)

2. физ. зависимость фазовой скорости волны от частоты ◆ Ещё более крупный шаг в этом направлении был сделан Н. П. Кастериным (1898, 1901, 1904), которому удалось проследить аналогию в явлениях дисперсии акустических и световых волн. П. Н. Лебедев, «Успехи акустики за последние десять лет», 1905 г. (цитата из НКРЯ)

3. физ. характеристика спектрометра, спектроскопа, дифракционной решётки ◆ Только для этого понадобится спектроскоп с очень большой дисперсией, то есть такой спектроскоп, в котором спектр растягивается на очень большую длину. М. П. Бронштейн, «Солнечное вещество», 1936 г. (цитата из НКРЯ)

6. в материаловедении — степень дисперсности, доля атомов в гетерогенной системе, находящихся на границе раздела фаз ◆ Эмульсия с высокой дисперсией.

Источник

Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel

Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Расчет дисперсии в Excel

Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

Среднеквадратичное (стандартное) отклонение

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:

На практике формула стандартного отклонения следующая:

Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

Расчет cреднеквадратичного (стандартного) отклонения в Excel

Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Расчет коэффициента вариации в Excel

Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:

Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Источник

Значение слова дисперсия

Словарь Ушакова

дисп е рсия, дисперсии, мн. нет, жен. (лат. dispersio).

1. Расхождение световых лучей разного цвета при прохождении сквозь преломляющую среду (оптика).

2. Состояние большего или меньшего раздробления вещества (ест.).

Современный экономический словарь. 1999

величина, характеризующая степень разброса количественных измерений индивидуальных участников статистической выборки (случайных величин) относительно среднего значения для этой выборки.

Начала Современного Естествознания. Тезаурус

(от лат. — рассеяние) — в широком смысле — мера рассеяния, отклонение от среднего; широко используется в математической статистике и теории вероятностей.

Словарь экономических терминов

величина, характеризующая степень разброса количественных измерений индивидуальных участников статистической выборки (случайных величин) относительно среднего значения для этой выборки.

Глоссарий телекоммуникационных терминов

Увеличение ширины импульса сигнала при его распространении по оптоволокну. Основной фактор, ограничивающий полосу пропускания многомодового оптоволокна.

Краткий словарь современных тектонических терминов

расхождение, рассеяние фрагментов континентальных блоков после раскола, дробления последних.

Тезаурус русской деловой лексики

Энциклопедический словарь

Словарь Ефремовой

Энциклопедия Брокгауза и Ефрона

или светорассеяние (см.) — расхождение преломленных лучей сложного цвета или при образовании цветовых спектров вследствие интерференции в явлениях дифракции и др. случаях; расхождение оптических осей для лучей разного цвета в двуосных кристаллах.

Большая Советская Энциклопедия

(от лат. dispersio ≈ рассеяние), в математической статистике и теории вероятностей, наиболее употребительная мера рассеивания, т. е. отклонения от среднего. В статистическом понимании Д.

есть среднее арифметическое из квадратов отклонений величин xi от их среднего арифметического

В теории вероятностей Д. случайной величины Х называется математическое ожидание Е (Х ≈ mх)2 квадрата отклонения Х от её математического ожидания mх= Е (Х). Д. случайной величины Х обозначается через D (X) или через s2X. Квадратный корень из Д. (т. е. s, если Д. есть s2) называется средним квадратичным отклонением (см. Квадратичное отклонение ).

Для случайной величины Х с непрерывным распределением вероятностей, характеризуемым плотностью вероятности р (х), Д. вычисляется по формуле

Лит.: Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969.

Источник

Дисперсия и ковариация: что это такое и в чем разница?

Здравствуйте, уважаемые читатели проекта Тюлягин! Сегодня речь пойдет о дисперсии и ковариации, двух на первый взгляд сложных понятий. Однако при более близком рассмотрении вы поймете что в них нет ничего сложного. Эти два термина чаще всего можно встретить в математике и статистике, однако они также используются в финансах и инвестициях. Об этом и поговорим далее в статье.

Содержание статьи:

Что такое дисперсия и ковариация

Дисперсия и ковариация — математические термины, часто используемые в статистике и теории вероятностей. Дисперсия это разброс набора данных вокруг его среднего значения, в то время как ковариация это мера направленного отношения между двумя случайными величинами.

В дополнение к их общему использованию в статистике, оба этих термина имеют также определенные значения для инвесторов, относящиеся к измерениям, проводимым на фондовом рынке, и распределению активов, оба из которых указаны ниже.

Дисперсия простыми словами

Дисперсия используется в статистике для описания разброса между набором данных от его среднего значения. Она рассчитывается путем нахождения взвешенного по вероятности среднего квадрата отклонений от ожидаемого значения. Таким образом, чем больше дисперсия, тем больше расстояние между числами в наборе и средним значением. И наоборот, меньшая дисперсия означает, что числа в наборе ближе к среднему.

Наряду со статистическим определением термин дисперсия также может использоваться в финансовом контексте. Многие биржевые эксперты и финансовые консультанты используют дисперсию акции для измерения ее волатильности. Возможность выразить, насколько далеко стоимость данной акции может отклониться от среднего значения, в одном числе — очень полезный индикатор того, насколько велик риск, с которым связана конкретная акция. Акция с более высокой дисперсией обычно сопряжена с большим риском и потенциалом для более высокой или более низкой доходности, в то время как акция с меньшей дисперсией может быть менее рискованной, что означает, что она будет иметь среднюю доходность.

Ковариация простыми словами

Ковариация — это мера того, как две случайные величины изменятся при сравнении друг с другом. Однако в финансовом или инвестиционном контексте термин ковариация описывает доходность двух разных инвестиций за период времени по сравнению с разными переменными. Эти активы обычно представляют собой рыночные ценные бумаги в портфеле инвестора, например акции.

Положительная ковариация означает, что доходность обоих инвестиций имеет тенденцию одновременно увеличиваться или уменьшаться в стоимости. С другой стороны, обратная или отрицательная ковариация означает, что доходности будут отдаляться друг от друга. Так, когда один актив поднимается, другой актив падает.

Ковариация может измерять движения двух переменных, но не указывает на степень, в которой эти две переменные изменяются по отношению друг к другу.
Ковариацию также можно использовать как инструмент для диверсификации портфеля инвестора. Для этого управляющий инвестиционным портфелем должен искать инвестиции, которые имеют отрицательную ковариацию друг с другом. Это означает, что когда доходность одного актива падает, доходность другого (связанного) актива повышается. Таким образом, покупка акций с отрицательной ковариацией — отличный способ минимизировать риск портфеля. Можно ожидать, что экстремальные пики и спады динамики акций уравновесят друг друга, что приведет к более стабильной норме доходности на протяжении многих лет.

Резюме

А на этом сегодня все про дисперсию и ковариацию, как видите это не так и сложно. Надеюсь статья была для вас полезной и интересной. Делитесь статьей в социальных сетях и мессенджерах и добавляйте сайт в закладки. Успехов и до новых встреч на страницах проекта Тюлягин!

Источник

Что такое дисперсия в статистике

Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.

Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.

Характеристики равномерного распределения представлены на картинке:

При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.

Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.

Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.

В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.

Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.

Виды дисперсии дискретной случайной величины

Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.

Общая дисперсия

Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.

Простая дисперсия, без разделения на группы:

Или в несколько преобразованном виде:

Взвешенная дисперсия, для вариационного ряда:

где x_i – значение из ряда;

f_i – частота, количество повторений;

n – число вариантов.

Черта сверху указывает на среднюю величину.

Межгрупповая дисперсия

Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».

Как найти данную дисперсию? По формуле:

где k – количество групп;

n_j – элементов в группе с индексом j.

Внутригрупповая дисперсия

Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».

Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.

В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.

Если вычислить среднюю величину от всех групповых,

то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.

Взаимосвязь

В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.

Свойства дисперсии

Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.

Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ 2 можно по отклонениям от фиксированного числа.

Уменьшение всех цифр в k раз приведет к падению D[X] в k 2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.

Показатели вариаций

Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:

Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.

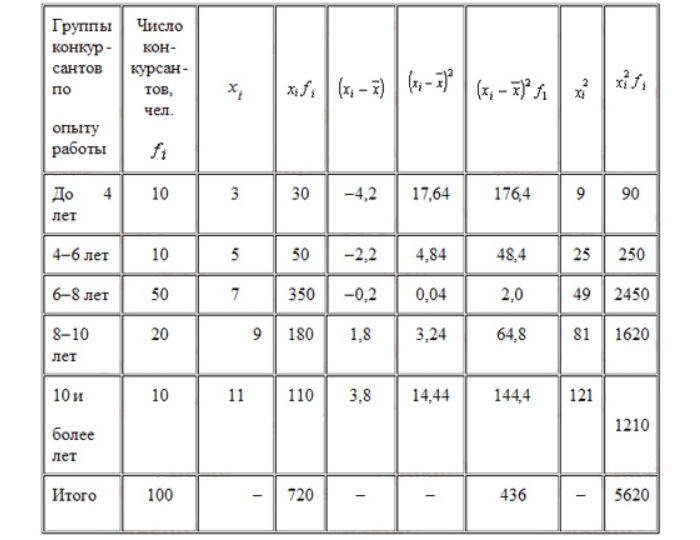
Пример расчета дисперсии

Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.

По альтернативной формуле:

Заключение

Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.

Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.

Источник