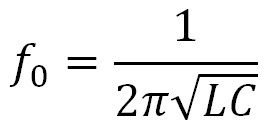Для чего фильтр низких частот
Электрический фильтр
Что такое электрический фильтр
Электрический фильтр — это устройство для выделения желательных компонентов спектра (частот) электрического сигнала и/или для подавления нежелательных. Для остальных частот, которые не входят в полосу пропускания, фильтр создает большое затухание, вплоть до полного их исчезновения.
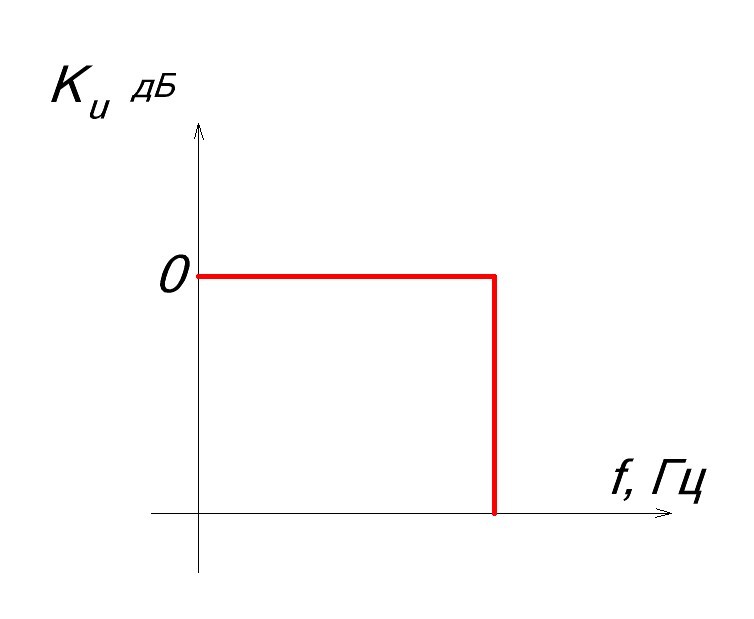
Характеристика идеального фильтра должна вырезать строго определенную полосу частота и «давить» другие частоты до полного их затухания. Ниже пример идеального фильтра, который пропускает частоты до какого-то определенного значения частоты среза.
На практике такой фильтр реализовать нереально. При проектировании фильтров стараются как можно ближе приблизиться к идеальной характеристике. Чем ближе характеристика АЧХ к идеальному фильтру, тем лучше он будет исполнять свою функцию фильтрации сигналов.
Фильтры, которые собираются только на пассивных радиоэлементах, таких как катушка индуктивности, конденсатор, резистор, называют пассивными фильтрами. Фильтры, которые в своем составе имеют один или несколько активных радиоэлементов, типа транзистора или ОУ, называют активными фильтрами.
В нашей статье мы будем рассматривать пассивные фильтры и начнем с самых простых фильтров, состоящих из одного радиоэлемента.
Одноэлементные фильтры
Как вы поняли из названия, одноэлементные фильтры состоят из одного радиоэлемента. Это может быть либо конденсатор, либо катушка индуктивности. Сами по себе катушка и конденсатор не являются фильтрами — это ведь по сути просто радиоэлементы. А вот вместе с выходным сопротивлением генератора и с сопротивлением нагрузки их уже можно рассматривать как фильтры. Здесь все просто. Реактивное сопротивление конденсатора и катушки зависят от частоты. Подробнее про реактивное сопротивление вы можете прочитать в этой статье.
В основном одноэлементные фильтры применяются в аудиотехнике. В этом случае для фильтрации используется либо катушка, либо конденсатор, в зависимости от того, какие частоты надо выделить. Для ВЧ-динамика (пищалки), мы последовательно с динамиком соединяем конденсатор, который будет пропускать через себя ВЧ-сигнал почти без потерь, а низкие частоты будет глушить.
Для сабвуферного динамика нам нужно выделить низкие частоты (НЧ), поэтому последовательно с сабвуфером соединяем катушку индуктивности.
Номиналы одиночных радиоэлементов можно, конечно, рассчитать, но в основном подбирают на слух.
Для тех, кто не желает заморачиваться, трудолюбивые китайцы создают готовые фильтры для пищалок и сабвуфера. Вот один из примеров:
На плате мы видим 3 клеммника: входной клеммник (INPUT), выходной под басы (BASS) и клеммник под пищалку (TREBLE).
Г-образные фильтры
Г-образные фильтры состоят из двух радиоэлементов, один или два из которых имеют нелинейную АЧХ.
RC-фильтры
Думаю, начнем с самого известного нам фильтра, состоящего из резистора и конденсатора. Он имеет две модификации:
С первого взгляда можно подумать, что это два одинаковых фильтра, но это не так. В этом легко убедиться, если построить АЧХ для каждого фильтра.
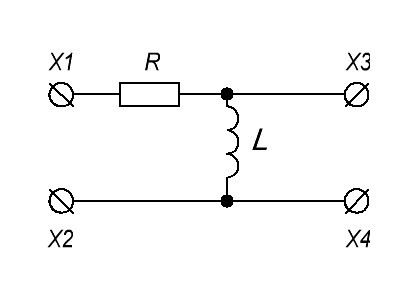
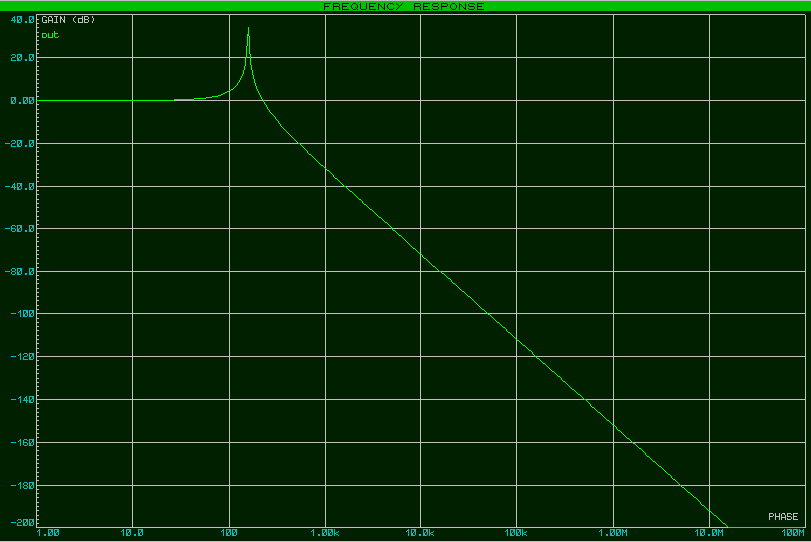
В этом деле нам поможет Proteus. Итак, АЧХ для этой цепи
будет выглядеть вот так:
Как мы видим, АЧХ такого фильтра беспрепятственно пропускает низкие частоты, а с ростом частоты ослабляет высокие частоты. Поэтому, такой фильтр называют фильтром низких частот (ФНЧ).
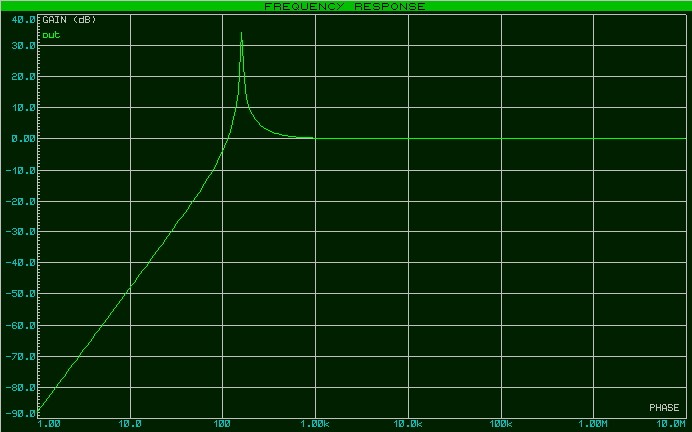
А вот для этой цепи
АЧХ будет выглядеть таким образом
Здесь как раз все наоборот. Такой фильтр ослабляет низкие частоты и пропускает высокие частоты, поэтому такой фильтр называется фильтром высокой частоты (ФВЧ).
Наклон характеристики АЧХ
Давайте рассмотрим этот пример
Чем больше крутизна наклона прямой АЧХ, тем лучше избирательные свойства фильтра:
Фильтр, с характеристикой наклона в 24 дБ/октаву явно будет лучше, чем в 6 дБ/октаву, так как становится более приближенным к идеальному.
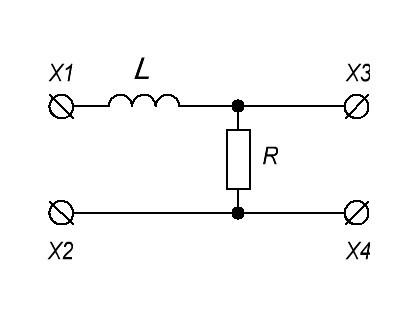
RL-фильтры
Почему бы не заменить конденсатор катушкой индуктивности? Получаем снова два типа фильтров:
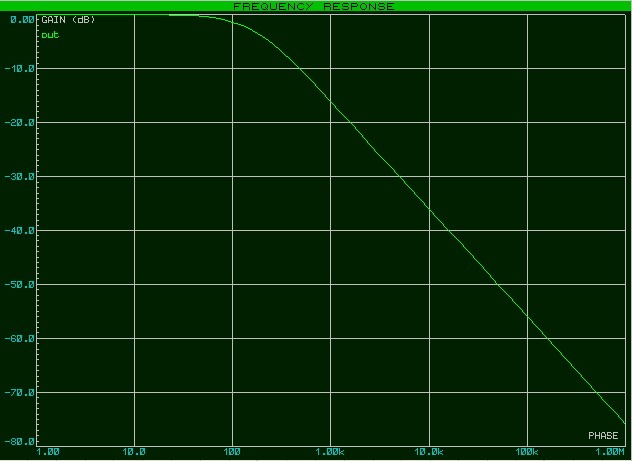
АЧХ принимает такой вид:
Получили все тот же самый ФНЧ
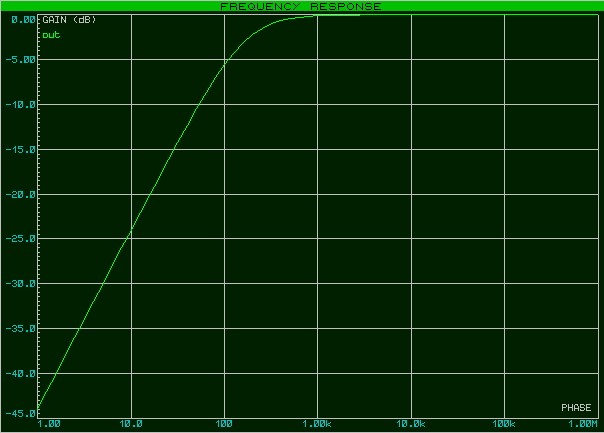
АЧХ примет такой вид
Тот же самый фильтр ФВЧ
RC и RL фильтры называют фильтрами первого порядка и они обеспечивают наклон характеристики АЧХ в 6 дБ/октаву после частоты среза.
LC-фильтры
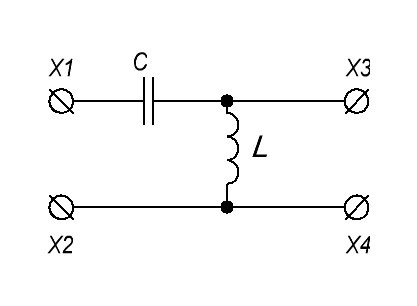
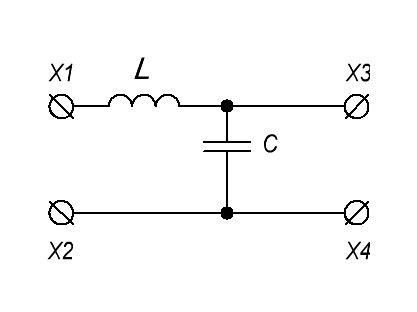
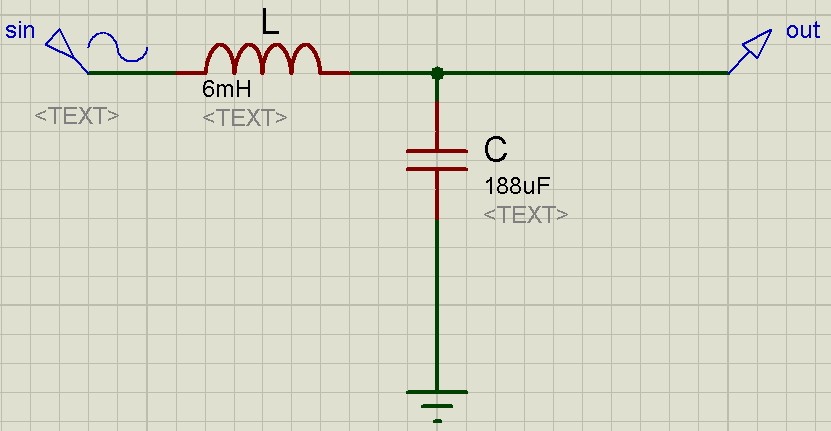
А что если заменить резистор конденсатором? Итого мы имеем в схеме два радиоэлемента, реактивное сопротивление которых зависит от частоты. Здесь получаются также два варианта:
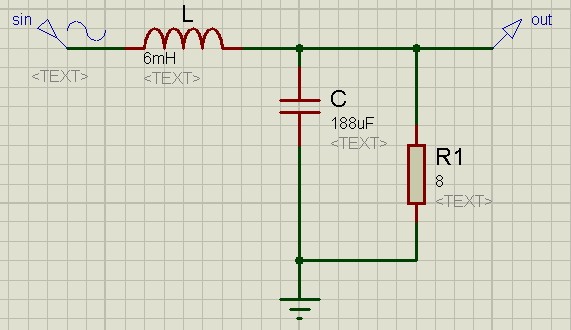
Давайте рассмотрим АЧХ этого фильтра
Как вы могли заметить, его АЧХ в области низких частот получилась наиболее плоской и заканчивается шипом. Откуда вообще он взялся? Мало того, что цепь собрана из пассивных радиоэлементов, так она еще и усиливает сигнал по напряжению в области шипа!? Но не стоит радоваться. Усиливает по напряжению, а не по мощности. Дело в том, что мы получили последовательный колебательный контур, у которого, как вы помните, на частоте резонанса возникает резонанс напряжений. При резонансе напряжений, напряжение на катушке равняется напряжению на конденсаторе.
Все то же самое касается и ФВЧ фильтра
Как я уже сказал, LC фильтры называют уже фильтрами второго порядка и они обеспечивают наклон АЧХ в 12 дБ/октаву.
Сложные фильтры
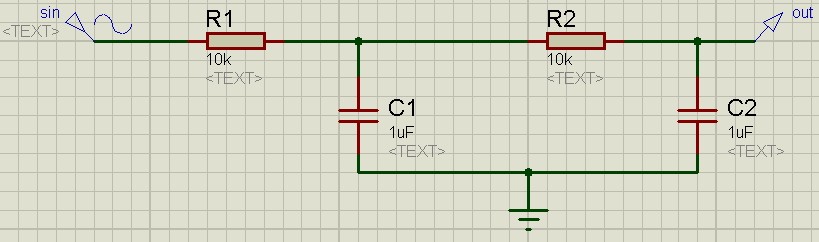
Что будет, если соединить два фильтра первого порядка друг за другом? Как ни странно, получится фильтр второго порядка.
В приведенных схемах мы строили АЧХ фильтра без внутреннего сопротивления генератора а также без нагрузки. То есть в данном случае сопротивление на выходе фильтра равняется бесконечности. Значит, желательно делать так, чтобы каждый последующий каскад имел значительно бОльшее входное сопротивление, чем предыдущий. В настоящее время каскадирование звеньев уже кануло в лету и сейчас используют активные фильтры, которые построены на ОУ.
Разбор фильтра с Алиэкспресс
Для того, чтобы вы уловили предыдущую мысль, мы разберем простой пример от наших узкоглазых братьев. На Алиэкпрессе продаются различные фильтры для сабвуфера. Рассмотрим один из них.
Как вы заметили, на нем написаны характеристики фильтра: данный тип фильтра рассчитан на сабвуфер мощностью 300 Ватт, наклон его характеристики 12 дБ/октаву. Если соединять к выходу фильтра саб с сопротивлением катушки в 4 Ома, то частота среза составит 150 Гц. Если же сопротивление катушки саба 8 Ом, то частота среза составит 300 Гц.
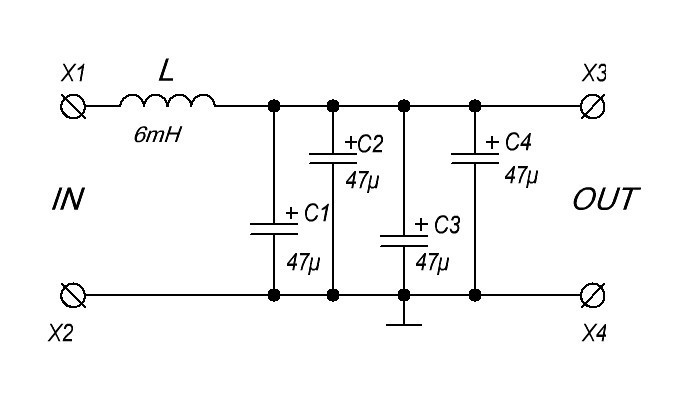
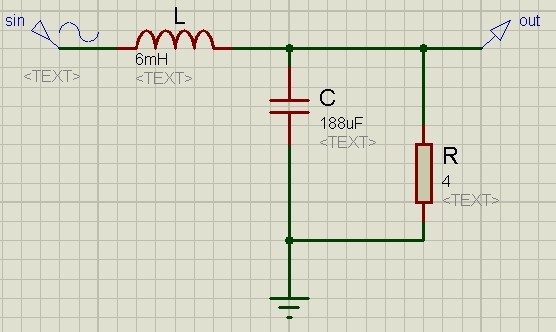
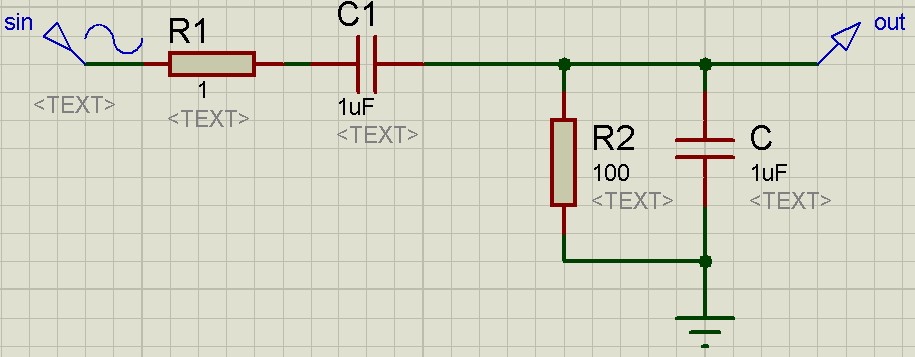
Для полных чайников продавец даже привел схему в описании товара. Выглядит она вот так:
Далее мы собираем эту схему в Proteus. Так как при параллельном соединении конденсаторов номиналы суммируются, я сразу заменил 4 конденсатора одним.
Чаще всего можно увидеть прямо на динамиках значение сопротивления катушки на постоянном токе: 2 Ω, 4 Ω, 8 Ω. Реже 16 Ω. Значок Ω после цифр обозначает Омы. Также не забывайте, что катушка в динамике обладает индуктивностью.
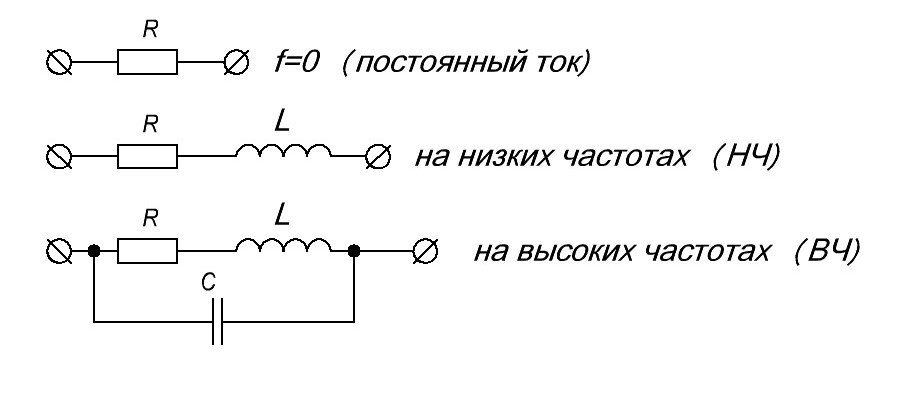
Как ведет себя катушка индуктивности на разных частотах?
Как вы видите, на постоянном токе катушка динамика обладает активным сопротивлением, так как она намотана из медного провода. На низких частотах в дело вступает реактивное сопротивление катушки, которое вычисляется по формуле:
ХL — сопротивление катушки, Ом
П — постоянная и равна приблизительно 3,14
Так как сабвуфер предназначен именно для низких частот, значит, последовательно с активным сопротивлением самой катушки добавляется реактивное сопротивление этой же самой катушки. Но в нашем опыте мы это учитывать не будем, так как не знаем индуктивность нашего воображаемого динамика. Поэтому, все расчеты в опыте берем с приличной погрешностью.
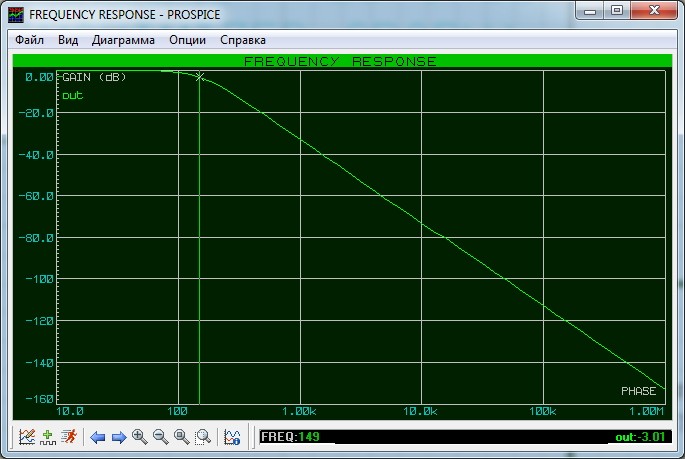
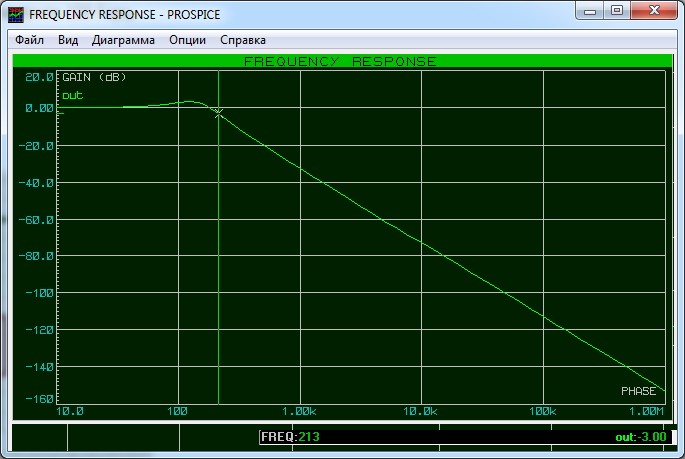
Как утверждает китаец, при нагрузке на фильтр динамика в 4 Ома, его полоса пропускания будет доходить до 150 Герц. Проверяем так ли это:
Нагружаем наш фильтр динамиком в 8 Ом
Частота среза составила 213 Гц.
В описании на товар утверждалось, что частота среза на 8-омный саб составит 300 Гц. Думаю, можно поверить китайцам, так как во-первых, все данные приближенные, а во-вторых, симуляция в программах далека от реальности. Но суть опыта была не в этом. Как мы видим на АЧХ, нагружая фильтр сопротивлением большего номинала, частота среза сдвигается в большую сторону. Это также надо учитывать при проектировании фильтров.
Полосовые фильтры
В прошлой статье мы с вами рассматривали один из примеров полосового фильтра
Вот так выглядит АЧХ этого фильтра.
Полосовые резонансные фильтры
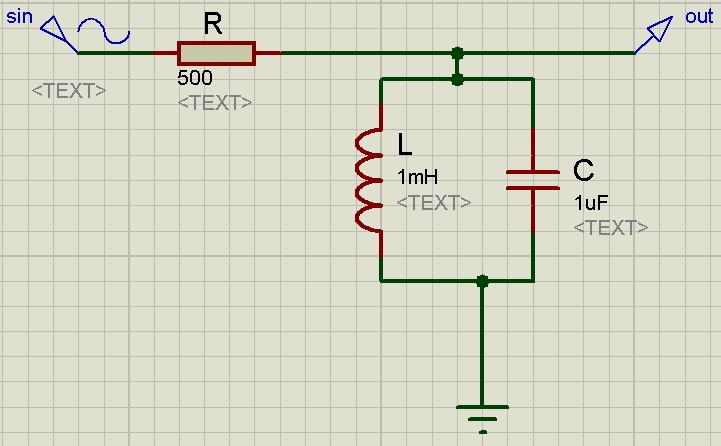
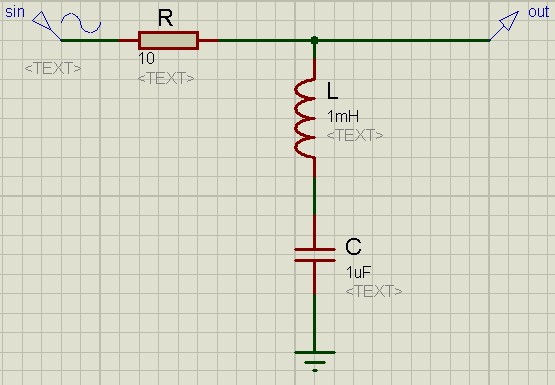
Если нам надо выделить какую-то узкую полосу частот, для этого применяются LC-резонанcные фильтры. Еще их часто называют избирательными. Давайте рассмотрим одного из их представителя.
LC-контур в сочетании с резистором R образует делитель напряжения. Катушка и конденсатор в паре создают параллельный колебательный контур, который на частоте резонанса будет иметь очень высокий импеданс, в народе — обрыв цепи. В результате, на выходе цепи при резонансе будет значение входного напряжения, при условии если мы к выходу такого фильтра не цепляем никакой нагрузки.
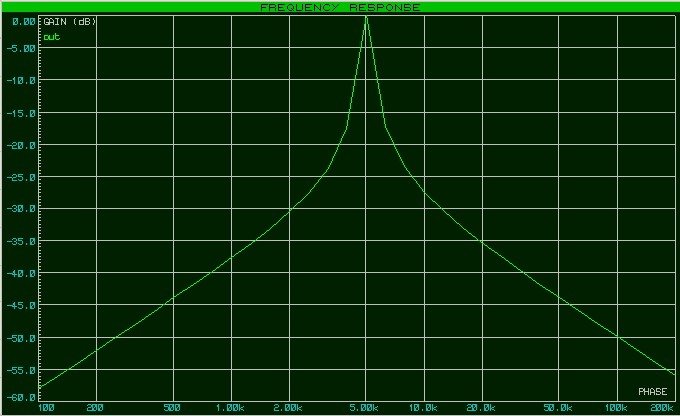
АЧХ данного фильтра будет выглядеть примерно вот так:
В реальной же цепи пик характеристики АЧХ будет сглажен за счет потерь в катушке и конденсаторе, так как катушка и конденсатор обладают паразитными параметрами.
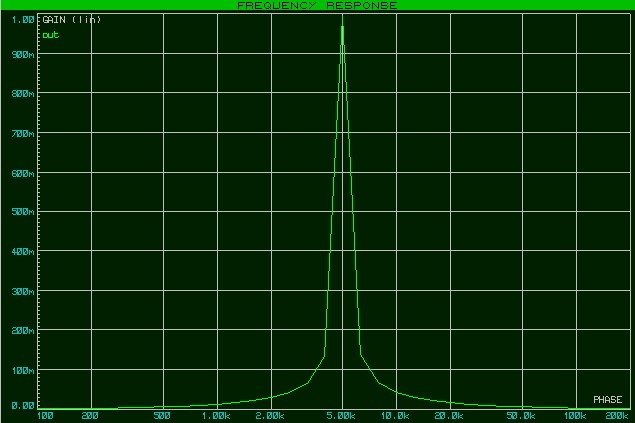
Если взять по оси Y значение коэффициента передачи, то график АЧХ будет выглядеть следующим образом:
Постройте прямую на уровне в 0,707 и оцените полосу пропускания такого фильтра. Как вы можете заметить, она будет очень узкой. Коэффициент добротности Q позволяет оценить характеристику контура. Чем большее добротность, тем острее характеристика.
Как же определить добротность из графика? Для этого надо найти резонансную частоту по формуле:
f0— это резонансная частота контура, Гц
L — индуктивность катушки, Гн
С — емкость конденсатора, Ф
Подставляем L=1mH и С=1uF и получаем для нашего контура резонансную частоту в 5033 Гц.
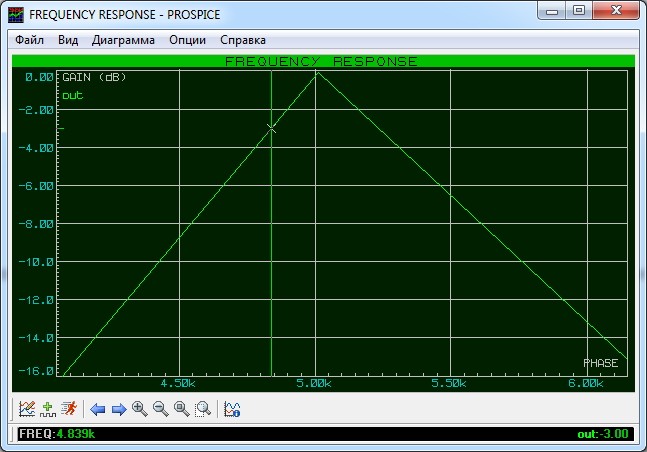
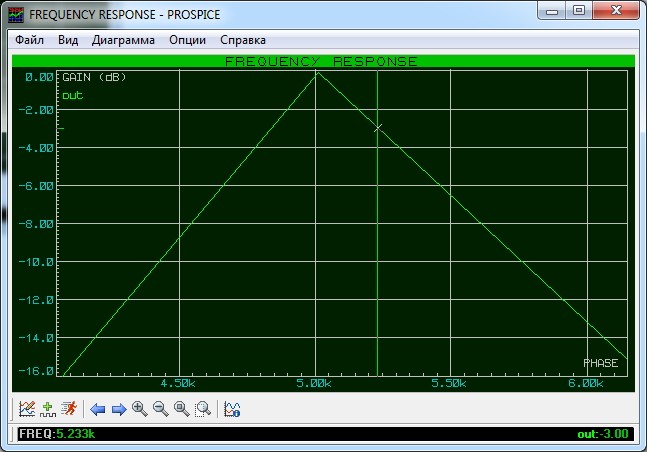
Давайте увеличим верхушку нашей АЧХ и найдем две частоты среза.
Следовательно, полоса пропускания Δf=f2 — f1 = 5233-4839=394 Гц
Ну и осталось найти добротность:
Режекторные фильтры
Другой разновидностью LC схем является последовательная LC-схема.
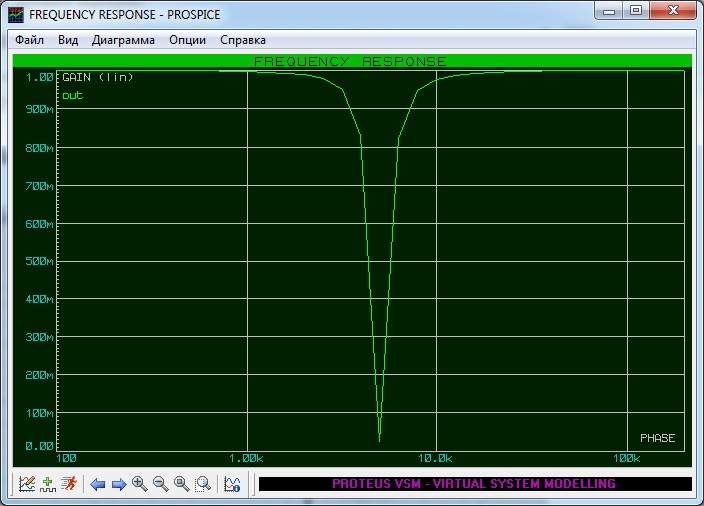
Ее АЧХ будет выглядеть примерно вот так:
Как можно увидеть, такая схема на резонансной частоте и вблизи нее как бы вырезает небольшой диапазон частот. Здесь вступает в силу резонанс последовательного колебательного контура. Как вы помните, на резонансной частоте сопротивление контура будет равняться его активному сопротивлению. Активное сопротивление контура составляют паразитные параметры катушки и конденсатора, поэтому падение напряжения на самом контуре будет равняться падению напряжения на паразитном сопротивлении, которое очень мало. Такой фильтр называют узкополосным режекторным фильтром.
На практике звенья таких фильтров каскадируют, чтобы получить различные фильтры с требуемой полосой пропускания. Но есть один минус у фильтров, в которых имеется катушка индуктивности. Катушки дорогие, громоздкие, имеют много паразитных параметров. Они чувствительны к фону, который магнитным путем наводится от расположенных поблизости силовых трансформаторов.
Конечно, этот недостаток можно устранить, поместив катушку индуктивности в экран из мю-металла, но от этого она станет только дороже. Проектировщики всячески пытаются избежать катушек индуктивности, если это возможно. Но, благодаря прогрессу, в настоящее время катушки не используются в активных фильтрах, построенных на ОУ.
Видео на тему «Как работает электрический фильтр», рекомендую к просмотру:
Заключение
В радиоэлектронике электрический фильтр находит множество применений. Например, в области электросвязи полосовые фильтры используются в диапазоне звуковой частоты (20 Гц-20 КГц). В системах сбора данных используются фильтры низких частот (ФНЧ). В музыкальной аппаратуре фильтры подавляют шумы, выделяют определенную группу частот для соответствующих динамиков, а также могут изменять звучание. В системах источников питания фильтры часто используются для подавления частот, близких к частоте сети 50/60 Герц. В промышленности фильтры применяются для компенсации косинуса фи, а также используются как фильтры гармоник.
Фильтр низких частот
Фильтр ни́жних часто́т (ФНЧ) — электронный или любой другой фильтр, эффективно пропускающий частотный спектр сигнала ниже некоторой частоты (частоты среза), и уменьшающий (или подавляющий) частоты сигнала выше этой частоты. Степень подавления каждой частоты зависит от вида фильтра.
В отличие от него, фильтр высоких частот пропускает частоты сигнала выше частоты среза, подавляя низкие частоты.
Реализация фильтров нижних частот может быть разнообразной, включая электронные схемы, программные алгоритмы, акустические барьеры, механические системы и т. д.
Содержание
Примеры фильтров нижних частот
Для звуковых волн твёрдый барьер играет роль фильтра нижних частот — например, в музыке, играющей в другой комнате, легко различимы басы, а высокие частоты отфильтровываются (звук «оглушается»). Точно так же ухом воспринимается музыка, играющая в закрытой машине.
Электронные фильтры нижних частот используются в сабвуферах и других типах звуковых колонок, в системах передачи данных для отфильтровки высокочастотных помех, а также имеют большое число других применений.
Радиопередатчики используют низкочастотные фильтры для блокировки гармонических излучений, которые могут взаимодействовать с низкочастотным полезным сигналом.
Механические низкочастотные фильтры часто используют в контурах непрерывных систем управления в качестве корректирующих звеньев.
В обработке изображений низкочастотные фильтры используются для очистки картинки от шума и создания спецэффектов, а также в сжатии изображений.
Идеальный фильтр нижних частот
Идеальный фильтр нижних частот (sinc-фильтр) полностью подавляет все частоты входного сигнала выше частоты среза и пропускает без изменений все частоты ниже частоты среза. Переходной зоны между частотами полосы подавления и полосы пропускания не существует. Идеальный фильтр нижних частот может быть реализован лишь теоретически с помощью умножения входного сигнала на прямоугольную функцию в частотной области, или, что даёт тот же эффект, свёртки сигнала во временно́й области с sinc-функцией.
Однако такой фильтр практически нереализуем для большинства сигналов, так как sinc-функция имеет ненулевые значения для всех моментов времени вплоть до бесконечности. Его можно использовать только для уже записанных цифровых сигналов либо для идеально периодических сигналов.
Реальные фильтры для приложений реального времени могут лишь приближаться к идеальному фильтру.
Для RC фильтра, применяемого на линейном входе компьютера, обычно используются переменный резистор и конденсатор емкостью около 0,33 мкФ.
См. также
Ссылки
Полезное
Смотреть что такое «Фильтр низких частот» в других словарях:
фильтр низких частот — — [В.А.Семенов. Англо русский словарь по релейной защите] Тематики релейная защита EN low pass filter … Справочник технического переводчика
фильтр низких частот — žemųjų dažnių filtras statusas T sritis automatika atitikmenys: angl. low pass filter vok. Tiefpaß, m; Tiefpaßfilter, n rus. фильтр низких частот, m pranc. filtre passe bas, m … Automatikos terminų žodynas
Фильтр высоких частот — Фильтр верхних частот (ФВЧ) электронный или любой другой фильтр, пропускающий высокие частоты входного сигнала, при этом подавляя частоты сигнала меньше, чем частота среза. Степень подавления зависит от конкретного типа фильтра. В отличие от ФВЧ … Википедия
Фильтр нижних частот — (ФНЧ) один из видов аналоговых или электронных фильтров, эффективно пропускающий частотный спектр сигнала ниже некоторой частоты (частоты среза), и уменьшающий (подавляющий) частоты сигнала выше этой частоты. Степень подавления каждой… … Википедия
фильтр верхних частот — Электрический частотный фильтр, имеющий полосу пропускания выше заданной частоты среза и полосу задерживания для более низких частот [ГОСТ 24375 80] фильтр верхних частот Фильтр, пропускающий сигналы с частотами выше граничной частоты и… … Справочник технического переводчика
Фильтр верхних частот — 1. Электрический частотный фильтр, имеющий полосу пропускания выше заданной частоты среза и полосу задерживания для более низких частот Употребляется в документе: ГОСТ 24375 80 … Телекоммуникационный словарь
Фильтр Саллена — Фильтр Саллена Кея один из типов активных электронных фильтров. Реализуется в виде простой схемы с двумя резисторами, двумя конденсаторами и активным элементом (например с операционным усилителем), представляя собой фильтр с… … Википедия
Фильтр Саллена-Кея — Фильтр Саллена Ки один из типов активных электронных фильтров. Реализуется в виде простой схемы с двумя резисторами, двумя конденсаторами и активным элементом (например с операционным усилителем), представляя собой фильтр с передаточной… … Википедия
Фильтр Чебышёва — Линейные электронные фильтры Фильтр Баттерворта Фильтр Чебышёва Эллиптический фильтр Фильтр Бесселя Фильтр Гаусса Фильтр Лежандра Фильтр Габора Править Фильтр Чебышёв … Википедия
ФИЛЬТР ЧАСТОТ — (англ. frequency filter) устройство, ослабляющее в сигнале определенные диапазоны частот; фильтр низких частот (англ. low frequency filter) ослабляет высокие частоты и пропускает низкие, тогда как фильтр высоких частот (англ. high frequency… … Большая психологическая энциклопедия
Что такое фильтр нижних частот? Руководство по основам пассивных RC фильтров
Что такое фильтрация? Рассмотрим, что представляют собой фильтры нижних частот из резисторов и конденсаторов (RC фильтры), и где их можно использовать.
Данная статья познакомит вас с концепцией фильтрации и подробно объяснит назначение и характеристики RC фильтров нижних частот.
Временная область и частотная область
Когда вы смотрите на электрический сигнал на осциллографе, вы видите линию, которая представляет изменения напряжения относительно времени. В любой конкретный момент времени сигнал имеет только одно значение напряжения. На осциллографе вы видите представление сигнала во временной области.
Типовая осциллограмма проста и интуитивно понятна, но она также имеет некоторые ограничения, поскольку она напрямую не раскрывает частотный состав сигнала. В отличие от представления во временной области, в котором один момент времени соответствует только одному значению напряжения, представление в частотной области (также называемое спектром) передает информацию о сигнале посредством определения различных частотных компонентов, которые представлены одновременно.
Рисунок 1 – Представления во временной области синусоидального (вверху) и прямоугольного (внизу) сигналов 
Рисунок 2 – Частотные представления синусоидального (вверху) и прямоугольного (внизу) сигналов
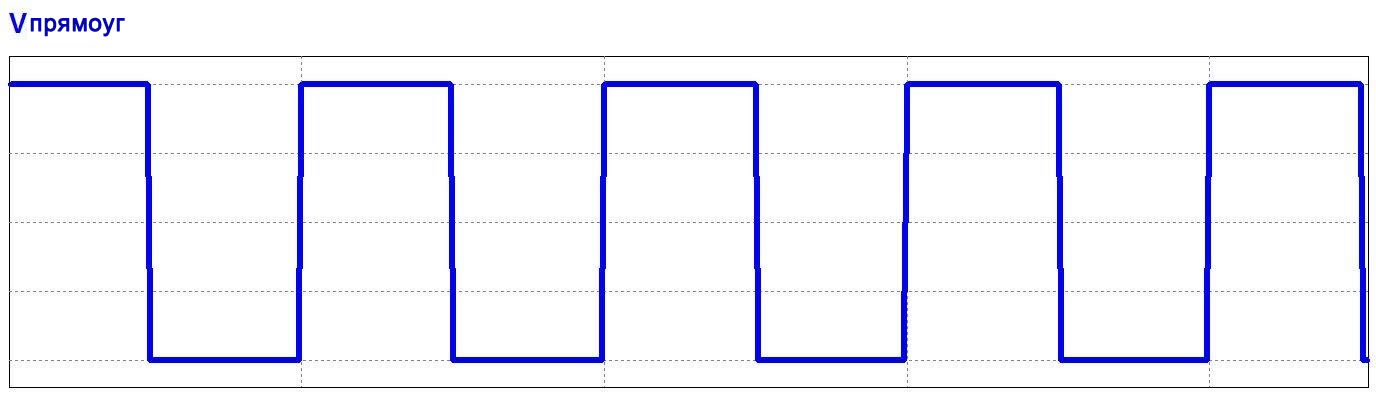
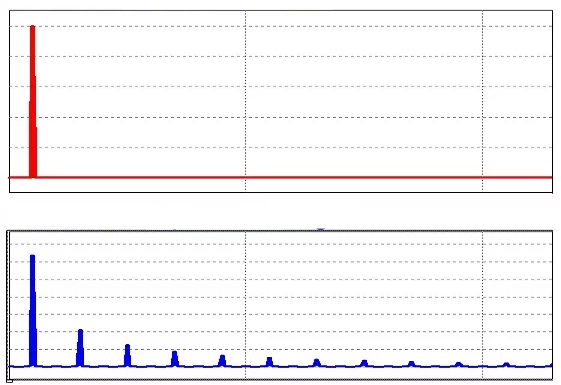
Что такое фильтр?
Фильтр – это схема, которая удаляет или «отфильтровывает» определенный диапазон частотных компонентов. Другими словами, он разделяет спектр сигнала на частотные составляющие, которые будут передаваться дальше, и частотные составляющие, которые будут блокироваться.
Если у вас нет большого опыта анализа частотной области, вы можете быть не уверены в том, что представляют собой эти частотные компоненты и как они сосуществуют в сигнале, который не может иметь несколько значений напряжения одновременно. Давайте рассмотрим краткий пример, который поможет прояснить эту концепцию.
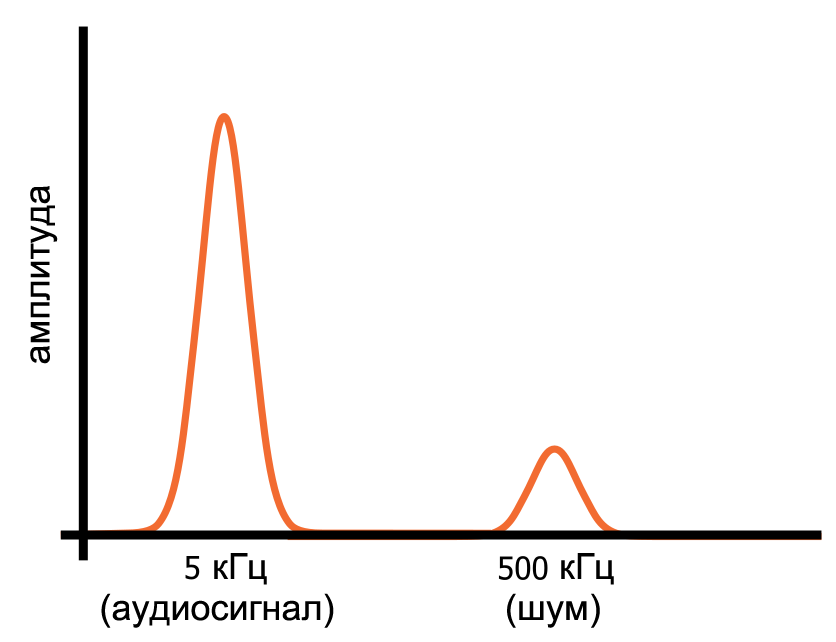
Давайте представим, что у нас есть аудиосигнал, который состоит из идеальной синусоидальной волны 5 кГц. Мы знаем, как выглядит синусоида во временной области, а в частотной области мы не увидим ничего, кроме частотного «всплеска» на 5 кГц. Теперь предположим, что мы включили генератор на 500 кГц, который вносит в аудиосигнал высокочастотный шум.
Сигнал, видимый на осциллографе, будет по-прежнему представлять собой только одну последовательность напряжений с одним значением на момент времени, но он будет выглядеть по-другому, поскольку его изменения во временной области теперь должны отражать как синусоидальную волну 5 кГц, так и высокочастотные колебания шума.
Однако в частотной области синусоида и шум являются отдельными частотными компонентами, которые присутствуют одновременно в этом одном сигнале. Синусоидальная волна и шум занимают разные участки представления сигнала в частотной области (как показано на диаграмме ниже), и это означает, что мы можем отфильтровать шум, направив сигнал через схему, которая пропускает низкие частоты и блокирует высокие частоты.
Рисунок 3 – Представление аудиосигнала и высокочастотного шума в частотной области
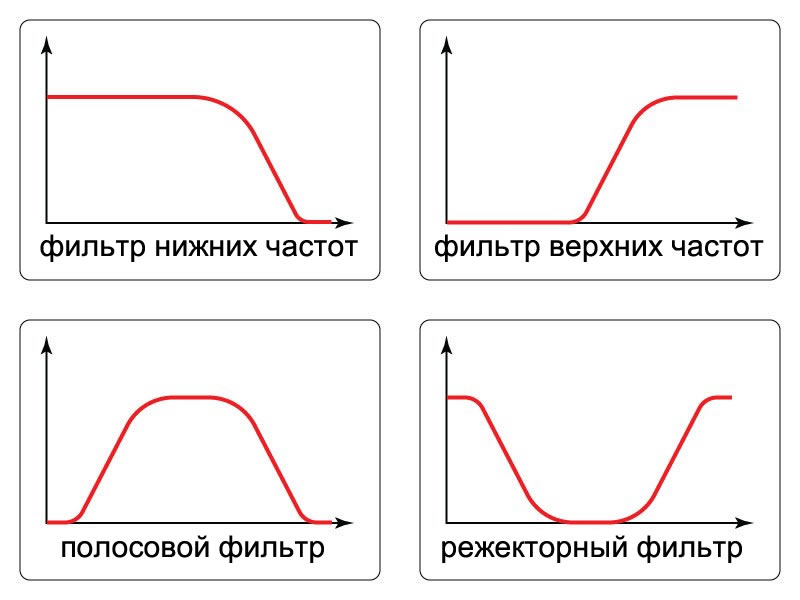
Типы фильтров
В зависимости от особенностей амплитудно-частотных характеристик фильтры можно распределить по широким категориям. Если фильтр пропускает низкие частоты и блокирует высокие частоты, он называется фильтром нижних частот. Если он блокирует низкие частоты и пропускает высокие частоты, это фильтр верхних частот. Существуют также полосовые фильтры, которые пропускают только относительно узкий диапазон частот, и режекторные фильтры, которые блокируют только относительно узкий диапазон частот.
Рисунок 4 – Амплитудно-частотные характеристики фильтров
Фильтры также могут быть классифицированы в соответствии с типами компонентов, которые используются для реализации схемы. Пассивные фильтры используют резисторы, конденсаторы и катушки индуктивности; эти компоненты не способны обеспечить усиление, и, следовательно, пассивный фильтр может только сохранять или уменьшать амплитуду входного сигнала. Активный фильтр, напротив, может фильтровать сигнал и применять усиление, поскольку он включает в себя активный компонент, такой как транзистор или операционный усилитель.
Рисунок 5 – Этот активный фильтр нижних частот основан на популярной топологии Саллена-Ки
В данной статье рассматривается анализ и проектирование пассивных фильтров нижних частот. Эти схемы играют важную роль в самых разных системах и приложениях.
RC фильтр нижних частот
Чтобы создать пассивный фильтр нижних частот, нам нужно объединить резистивный элемент с реактивным элементом. Другими словами, нам нужна схема, которая состоит из резистора и либо конденсатора, либо катушки индуктивности. Теоретически, топология фильтров нижних частот резистор-индуктивность (RL) эквивалентна, с точки зрения фильтрующей способности, топологии фильтров нижних частот резистор-конденсатор (RC). Однако на практике версия резистор-конденсатор встречается гораздо чаще, и, следовательно, оставшаяся часть этой статьи будет посвящена RC фильтру нижних частот.
Рисунок 6 – RC фильтр нижних частот
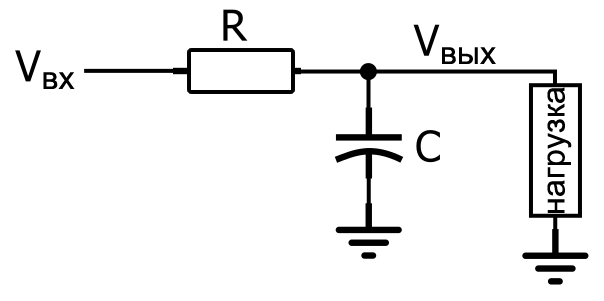
Как вы можете видеть на схеме, пропускающая нижние частоты частотная характеристика RC фильтра создается путем установки резистора последовательно с путем прохождения сигнала и конденсатора параллельно нагрузке. На схеме нагрузка является отдельным компонентом, но в реальной цепи она может представлять что-то гораздо более сложное, например, аналого-цифровой преобразователь, усилитель или входной каскад осциллографа, который вы используете для измерения амплитудно-частотной характеристики фильтра.
Мы можем интуитивно проанализировать фильтрующее действие топологии RC фильтра нижних частот, если поймем, что резистор и конденсатор образуют частотно-зависимый делитель напряжения.
Рисунок 7 – RC фильтр нижних частот перерисован так, чтобы он выглядел как делитель напряжения
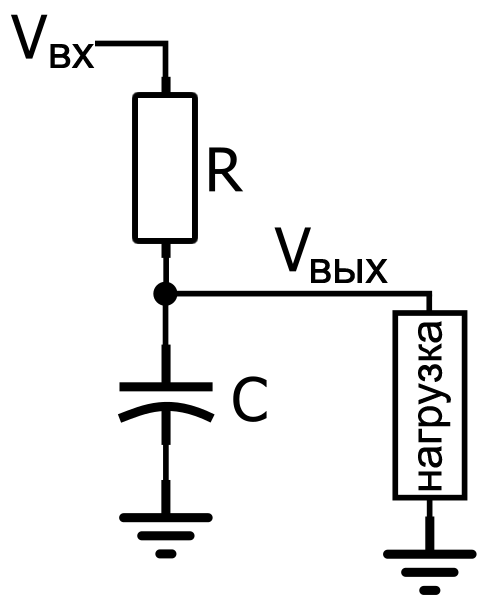
Когда частота входного сигнала низкая, полное сопротивление конденсатора будет высоким относительно полного сопротивления резистора; таким образом, большая часть входного напряжения падает на конденсаторе (и на нагрузке, которая параллельна конденсатору). Когда входная частота высокая, полное сопротивление конденсатора будет низким по сравнению с полным сопротивлением резистора, что означает, что на резисторе падает большее напряжение, и меньшее напряжение передается на нагрузку. Таким образом, низкие частоты пропускаются, а высокие частоты блокируются.
Это качественное объяснение работы RC фильтра нижних частот является важным первым шагом, но оно не очень полезно, когда нам нужно проектировать реальную схему, потому что термины «высокая частота» и «низкая частота» чрезвычайно расплывчаты. Инженеры должны создавать схемы, которые пропускают и блокируют определенные частоты. Например, в аудиосистеме, описанной выше, мы хотим сохранить сигнал 5 кГц и подавить сигнал 500 кГц. Это означает, что нам нужен фильтр, который переходит от пропускания к блокировке где-то между 5 кГц и 500 кГц.
Частота среза
Диапазон частот, для которого фильтр не вызывает значительного ослабления, называется полосой пропускания, а диапазон частот, для которых фильтр вызывает существенное ослабление, называется полосой задерживания. Аналоговые фильтры, такие как RC фильтр нижних частот, переходят из полосы пропускания в полосу задерживания всегда постепенно. Это означает, что невозможно идентифицировать одну частоту, на которой фильтр прекращает пропускать сигналы и начинает их блокировать. Однако инженерам нужен способ, чтобы удобно и кратко охарактеризовать амплитудно-частотную характеристику фильтра, и именно здесь в игру вступает понятие частоты среза.
Когда вы посмотрите на график амплитудно-частотной характеристики RC фильтра, вы заметите, что термин «частота среза» не очень точен. Изображение спектра сигнала, «разрезанного» на две половины, одна из которых сохраняется, а другая отбрасывается, неприменимо, поскольку затухание увеличивается постепенно по мере того, как частоты перемещаются от значений ниже частоты среза к значениям выше частоты среза.
Как объяснялось выше, пропускающее низкие частоты поведение RC фильтра обусловлено взаимодействием между частотно-независимым импедансом резистора и частотно-зависимым импедансом конденсатора. Чтобы определить подробности амплитудно-частотной характеристики фильтра, нам нужно математически проанализировать взаимосвязь между сопротивлением (R) и емкостью (C); мы также можем манипулировать этими значениями, чтобы разработать фильтр, который соответствует точным спецификациям. Частота среза (fср) RC фильтра нижних частот рассчитывается следующим образом:
Давайте посмотрим на простой пример. Значения конденсаторов являются более сдерживающими, чем значения резисторов, поэтому мы начнем с распространенного значения емкости (например, 10 нФ), а затем воспользуемся формулой для определения необходимого значения сопротивления. Цель состоит в том, чтобы разработать фильтр, который будет сохранять аудиосигнал 5 кГц и подавлять шум 500 кГц. Мы попробуем частоту среза 100 кГц, а позже в этой статье мы более тщательно проанализируем влияние этого фильтра на обе частотные составляющие.
Таким образом, резистор 160 Ом в сочетании с конденсатором 10 нФ даст нам фильтр, который дает амплитудно-частотную характеристику, близкую к необходимой.
Расчет амплитудно-частотной характеристики фильтра
Мы можем рассчитать теоретическое поведение фильтра нижних частот, используя частотно-зависимую версию типового расчета делителя напряжения. Выходное напряжение резистивного делителя напряжения выражается следующим образом:
Рисунок 9 – Резистивный делитель напряжения
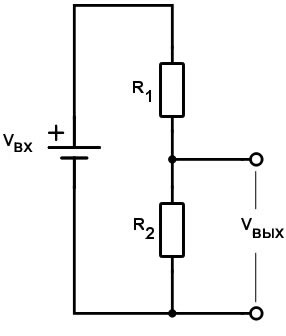
RC фильтр использует эквивалентную структуру, но вместо R2 у нас конденсатор. Сначала мы заменим R2 (в числителе) на реактивное сопротивление конденсатора (XC). Далее нам нужно рассчитать величину полного сопротивления и поместить его в знаменатель. Таким образом, мы имеем
Реактивное сопротивление конденсатора указывает величину противодействия протеканию тока, но, в отличие от активного сопротивления, величина противодействия зависит от частоты сигнала, проходящего через конденсатор. Таким образом, мы должны рассчитать реактивное сопротивление на определенной частоте, и формула, которую мы используем для этого, следующая:
В приведенном выше примере схемы R ≈ 160 Ом, и C = 10 нФ. Предположим, что амплитуда Vвх равна 1 В, поэтому мы можем просто удалить Vвх из расчетов. Сначала давайте рассчитаем амплитуду Vвых на частоте необходимой нам синусоиды:
Амплитуда необходимого нам синусоидального сигнала практически не изменяется. Это хорошо, поскольку мы намеревались сохранить синусоидальный сигнал при подавлении шума. Этот результат неудивителен, поскольку мы выбрали частоту среза (100 кГц), которая намного выше частоты синусоидального сигнала (5 кГц).
Теперь посмотрим, насколько успешно фильтр ослабит шумовую составляющую.
Амплитуда шума составляет всего около 20% от первоначального значения.
Визуализация амплитудно-частотной характеристики фильтра
Наиболее удобным способом оценки влияния фильтра на сигнал является изучение графика его амплитудно-частотной характеристики. На этих графиках, часто называемых графиками Боде, амплитуда (в децибелах) откладывается по вертикальной оси, а частота – по горизонтальной оси; горизонтальная ось обычно имеет логарифмический масштаб, поэтому физическое расстояние между 1 Гц и 10 Гц такое же, как физическое расстояние между 10 Гц и 100 Гц, между 100 Гц и 1 кГц и так далее. Такая конфигурация позволяет нам быстро и точно оценить поведение фильтра в очень широком диапазоне частот.
Рисунок 10 – Пример графика амплитудно-частотной характеристики
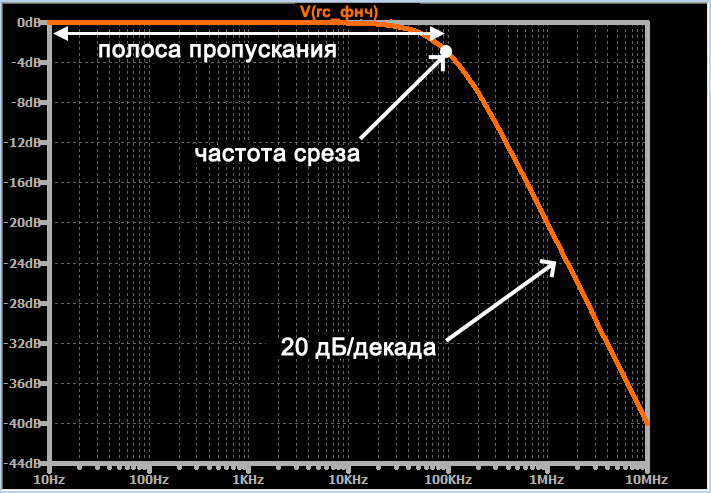
Каждая точка на кривой указывает амплитуду, которую будет иметь выходной сигнал, если входной сигнал имеет величину 1 В и частоту, равную соответствующему значению на горизонтальной оси. Например, когда частота входного сигнала равна 1 МГц, амплитуда выходного сигнала (при условии, что амплитуда входного сигнала равна 1 В) будет 0,1 В (поскольку –20 дБ соответствует уменьшению в десять раз).
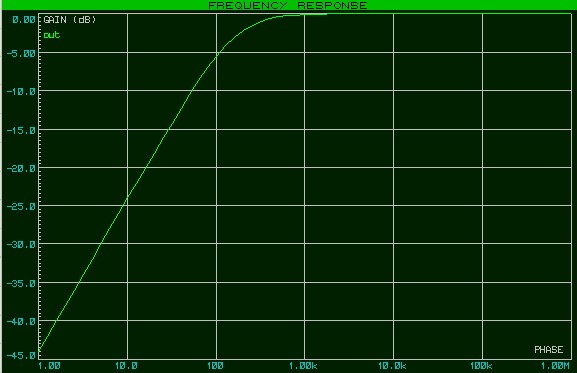
Общий вид этой кривой амплитудно-частотной характеристики станет вам очень знакомым, если вы будете проводить больше времени со схемами фильтров. Кривая почти идеально плоская в полосе пропускания, а затем, по мере приближения частоты входного сигнала к частоте среза, скорость ее спада начинает увеличиваться. В конечном итоге скорость изменения затухания, называемая спадом, стабилизируется на уровне 20 дБ/декада, то есть уровень выходного сигнала уменьшается на 20 дБ при каждом увеличении частоты входного сигнала в десять раз.
Оценка производительности фильтра нижних частот
Если мы построим амплитудно-частотную характеристику фильтра, который мы разработали ранее в этой статье, то увидим, что амплитудный отклик на 5 кГц, по сути, равен 0 дБ (т.е. почти нулевое затухание), а амплитудный отклик на 500 кГц составляет приблизительно –14 дБ (что соответствует коэффициенту передачи 0,2). Эти значения согласуются с результатами расчетов, которые мы выполнили в предыдущем разделе.
Поскольку RC фильтры всегда имеют плавный переход от полосы пропускания к полосе задерживания, а затухание никогда не достигает бесконечности, мы не можем разработать «идеальный» фильтр, то есть фильтр, который не влияет на необходимый синусоидальный сигнал и полностью устраняет шум. Вместо этого у нас всегда есть компромисс. Если мы сместим частоту среза ближе к 5 кГц, то получим большее затухание шума, но так же и большее затухание полезного синусоидального сигнала, который мы хотим отправить на динамик. Если мы переместим частоту среза ближе к 500 кГц, то получим меньшее затухание на частоте полезного сигнала, но так же и меньшее затухание на частоте шума.
Фазовый сдвиг фильтра низких частот
До сих пор мы обсуждали способ, которым фильтр изменяет амплитуду различных частотных составляющих в сигнале. Однако реактивные элементы цепи в дополнение к влиянию на амплитуду всегда вносят сдвиг фазы.
Понятие фазы относится к значению периодического сигнала в определенный момент цикла. Таким образом, когда мы говорим, что схема вызывает сдвиг фазы, то имеем в виду, что она создает смещение между входным и выходным сигналами: входной и выходной сигналы больше не начинают и заканчивают свои циклы в один и тот же момент времени. Значение сдвига фазы, например, 45° или 90°, показывает, какое было создано смещение.
Каждый реактивный элемент в цепи вводит сдвиг фазы на 90°, но этот фазовый сдвиг происходит не сразу. Фаза выходного сигнала, так же как и амплитуда выходного сигнала, изменяется постепенно по мере увеличения частоты входного сигнала. В RC фильтре нижних частот у нас есть один реактивный элемент (конденсатор), и, следовательно, схема в конечном итоге будет вводить сдвиг фазы на 90°.
Как и в случае амплитудно-частотной характеристикой, фазо-частотную характеристику легче всего оценить, изучив график, на котором частота на горизонтальной оси приведена в логарифмическом масштабе. Приведенное ниже описание дает общее представление, а затем вы можете заполнить детали, изучив график.
Фильтры нижних частот второго порядка
До сих пор мы предполагали, что RC фильтр нижних частот состоит из одного резистора и одного конденсатора. Эта конфигурация является фильтром первого порядка.
«Порядок» пассивного фильтра определяется количеством реактивных элементов, то есть конденсаторов или индуктивностей, которые присутствуют в цепи. Фильтр более высокого порядка имеет больше реактивных элементов, что приводит к большему сдвигу фазы и более крутому спаду АЧХ. Эта вторая характеристика является основной причиной для увеличения порядка фильтра.
Добавляя один реактивный элемент к фильтру, например, переходя от первого порядка ко второму или от второго к третьему, мы увеличиваем максимальный спад на 20 дБ/декада. Более крутой спад приводит к более быстрому переходу от низкого затухания к высокому затуханию, и это может привести к улучшению производительности, когда нет широкой полосы частот, отделяющей необходимые частотные компоненты от шумовых компонентов.
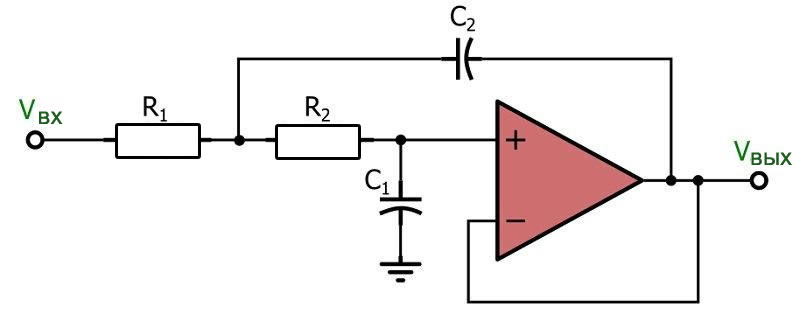
Фильтры второго порядка обычно строятся вокруг резонансного контура, состоящего из катушки индуктивности и конденсатора (эта топология называется «RLC», т.е. резистор-индуктивность-конденсатор). Однако также возможно создание RC фильтров второго порядка. Как показано на рисунке ниже, всё, что нам нужно сделать, это включить каскадно два RC фильтра первого порядка.
Рисунок 12 – RC фильтр нижних частот второго порядка
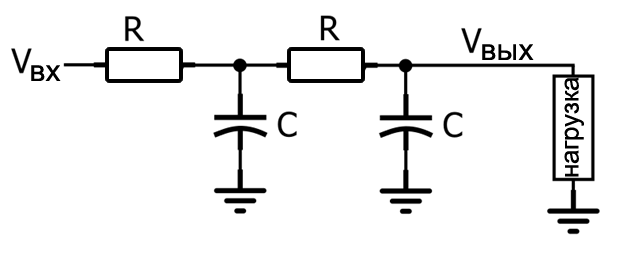
Хотя эта топология, безусловно, создает характеристику второго порядка, она широко не используется – как мы увидим в следующем разделе, ее амплитудно-частотная характеристика часто уступает амплитудно-частотной характеристике активного фильтра второго порядка или RLC фильтра второго порядка.
Амплитудно-частотная характеристика RC фильтра второго порядка
Мы можем попытаться создать RC фильтр нижних частот второго порядка, разработав фильтр первого порядка в соответствии с необходимой частотой среза, а затем соединив два этих каскада первого порядка последовательно. Это даст фильтр, который имеет аналогичную общую амплитудно-частотную характеристику и максимальный спад 40 дБ/декада вместо 20 дБ/декада.
Однако если мы посмотрим на АЧХ более внимательно, то увидим, что частота –3 дБ снизилась. RC фильтр второго порядка ведет себя не так, как ожидалось, поскольку эти два звена не являются независимыми – мы не можем просто соединить эти две звена вместе и проанализировать схему как фильтр нижних частот первого порядка, за которым следует идентичный фильтр нижних частот первого порядка.
Кроме того, даже если мы вставим буфер между этими двумя звеньями, чтобы первое RC звено и второе RC звено могли работать как независимые фильтры, затухание на исходной частоте среза будет составлять 6 дБ вместо 3 дБ. Это происходит именно потому, что два звена работают независимо – первый фильтр вносит затухание 3 дБ на частоте среза, а второй фильтр добавляет еще 3 дБ затухания.
Рисунок 13 – Сравнение амплитудно-частотных характеристик фильтров нижних частот второго порядка
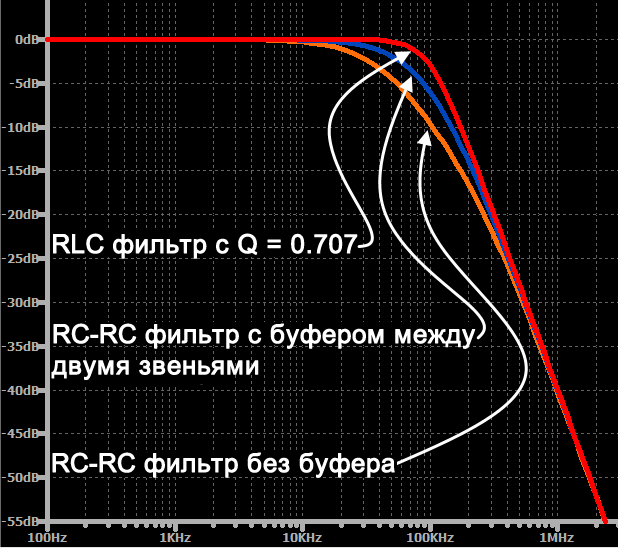
Основное ограничение RC фильтра нижних частот второго порядка состоит в том, что разработчик не может точно настроить переход от полосы пропускания к полосе задерживания, регулируя добротность (Q) фильтра; этот параметр указывает, насколько сглажена амплитудно-частотная характеристика. Если вы каскадно соединяете два идентичных RC фильтра нижних частот, общая передаточная функция соответствует отклику второго порядка, но добротность всегда равна 0,5. Когда Q = 0,5, фильтр находится на границе чрезмерного затухания, и это приводит к амплитудно-частотной характеристике, которая «провисает» в переходной области. Активные фильтры второго порядка и резонансные фильтры второго порядка не имеют такого ограничения; разработчик может управлять добротностью и, таким образом, точно настраивать амплитудно-частотную характеристику в переходной области.