Для чего формулы ускорения a v v0 t

Ускорение. Равноускоренное движение

Что такое ускоренное движение

Ускоренное движение — что это такое? Хороший вопрос. Давайте разберем это понятие по словам.

«Движение» — значит, что-то двигается. Ага, значит тело перемещается, значит у него есть какая-то скорость.

«Ускоренное» — значит «убыстренное», с возрастающей скоростью, когда тело двигается все быстрее и быстрее. Ага, значит скорость не постоянная. Она меняется. Тело двигается все быстрее, быстрее и быстрее. То есть скорость все время увеличивается.

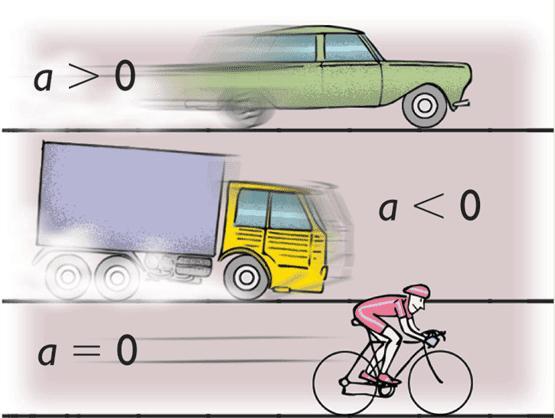
Чтобы быть конкретнее, посмотрим на пример: мальчик на велосипеде разгоняется из состояния покоя. Сначала у него скорость 5 5 5 км/ч, потом 1 0 10 1 0 км/ч, потом 1 5 15 1 5 км/ч, 2 0 20 2 0 км/ч, 2 5 25 2 5 км/ч, 3 0 30 3 0 км/ч и т.д. — насколько у него хватит сил.

Точно так же, как мальчик разгоняется на велосипеде, кто-то, например девочка на самокате, может тормозить, останавливаться, двигаться все медленнее, медленнее и медленнее. В конце — остановиться. Сначала у нее может быть скорость 1 0 10 1 0 км/ч, потом 5 5 5 км/ч, а потом 0 0 0 км/ч. То есть скорость все время уменьшается на 5 5 5 км/ч.

Вернемся к примеру с девочкой. Мы видим, что ее скорость начинает возрастать в отрицательном направлении. То есть наше замедленное движение девочки на самокате переходит в ускоренное движение (когда скорость набирается), но уже в противоположную сторону. Именно поэтому замедленное движение — это вариант ускоренного движения. Поэтому между ускоренным и замедленным движениями (как правило) не делают различий и называют их просто ускоренным движением.

В итоге мы пришли к тому, что ускоренное движение — это движение, при котором меняется скорость. Но мы помним, что скорость — это векторная величина. А любой вектор характеризуется двумя величинами: длиной и направлением. Так вот, оказывается, что тело движется с ускорением в случае, если меняется скорость по величине (тело убыстряет свое движение) или же тело меняет направление скорости (тело поворачивает). Первый случай (с изменением величины — или, как говорят, модуля) мы рассмотрим сейчас в теме «Равноускоренное движение», а второй случай — с поворотом — в теме «Движение по окружности», когда тело поворачивает, а значит — изменяет направление скорости.

Ускорение

— это очень полезная для нас формула. Ее нужно запомнить.

Источник

Ускорение при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v ₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

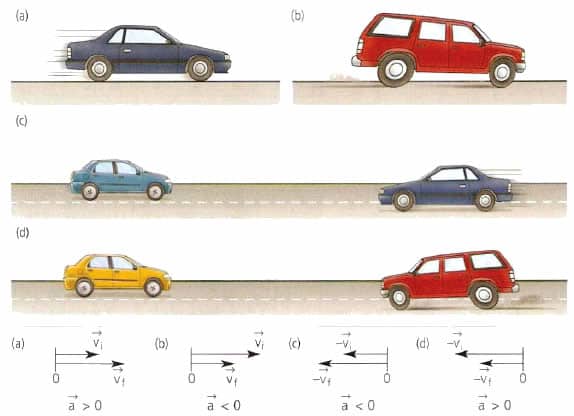
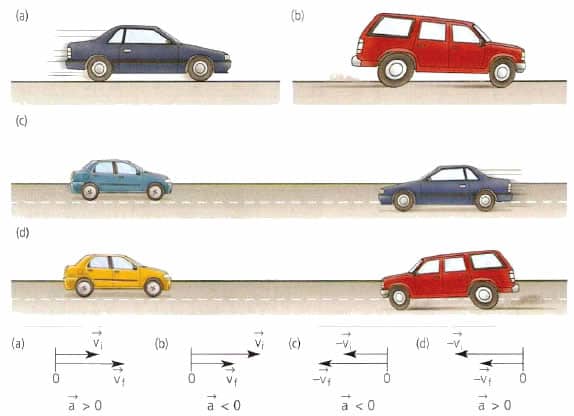
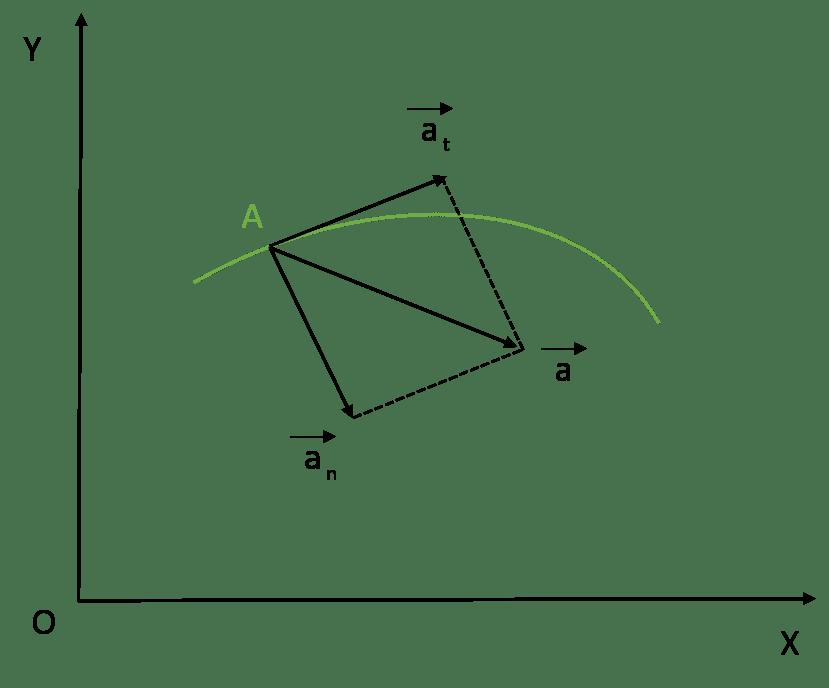
Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают ( а ↑↑ v ).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу ( а ↑↓ v ).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁ = 1 и t₂ = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Запишем исходные данные:

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Внимательно прочитайте текст задани я и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

Подставляем данные формулу и вычисляем модуль ускорения:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Что такое ускорение? Формулы ускорения при равноускоренном движении по прямой траектории

Ускорение и причина его появления

В физике величину, которая характеризует изменение во времени скорости, называют ускорением. Математическая формула для ускорения выглядит так:

Чем быстрее изменяется скорость, тем больше будет ускорение тела. Например, значение a = 1 м/с2 говорит о том, что за 1 секунду скорость увеличилась на 1 м/с.

Ускорение у тел возникает за счет действия на них внешних сил любой природы. Этот факт был установлен Ньютоном в XVII веке. В настоящее время он носит название 2-го закона Ньютона:

Обе формулы говорят о том, что вектор ускорения направлен в сторону изменения вектора скорости или в сторону вектора силы (F¯ и dv¯ направлены одинаково). Если направления векторов a¯ и v¯ совпадают, тогда тело будет ускоряться, если они противоположны, то тело будет замедлять свое движение, если же они направлены под некоторым углом, тогда траектория перемещения будет кривой линией.

Равноускоренное прямолинейное движение. Скорость и ускорение

Указанный вид движения предполагает, что траектория тела является прямой линией, а величина ускорения в процессе перемещения тела не изменяется ни по модулю, ни по направлению. Поскольку тело движется по прямой линии, то векторы a¯ и v¯ направлены либо в одну сторону, либо в противоположные.

Предположим, что тело находилось в покое. Затем на него начала действовать постоянная сила, которая придала ему ускорение. В таком случае скорость v в любой момент времени t может быть вычислена так:

Где a = const. Графиком этого уравнения является возрастающая прямая, которая начинается с точки (v=0; t=0).

Если же тело до начала действия силы уже имело некоторую скорость v0, тогда будут справедливы такие формулы:

Из последних двух выражений можно получить формулы ускорения при равноускоренном движении тела по прямой линии:

Время t отсчитывается от момента действия силы на тело.

Ускорение и путь

При решении задач на равноускоренное перемещение часто требуется найти ускорение, зная пройденный путь. Покажем, какие формулы для этого следует применять.

Путь рассчитать несложно при равноускоренном движении по прямой. Для этого следует взять интеграл по времени от уравнения v(t). Выполнив это математическое действие, получим три рабочие формулы:

Как выразить ускорение из формул равноускоренного движения для пути? Для этого необходимо изолировать множитель a*t2 в одной части равенства, а затем все равенство поделить на квадрат времени. Из формул выше получаем:

Первое уравнение используется для экспериментального определения ускорения свободного падения g, когда тяжелые тела сбрасывают вниз с некоторой высоты. Подобные эксперименты проводил еще Галилей в конце XVI века. В настоящее время для определения ускорения g в исследуемой местности используют абсолютные гравиметры, принцип работы которых также основан на свободном падении.

Два последних уравнения отличаются друг от друга лишь знаком ускорения. При торможении ускорение считают отрицательным.

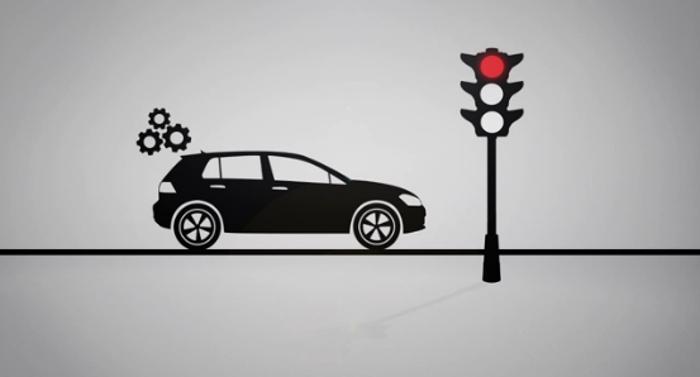
Задача на вычисление ускорения

Разобравшись с основными формулами ускорения при равноускоренном движении, решим следующую проблему практического характера: водитель автомобиля, который двигался со скоростью 63 км/ч, увидел, что впереди загорелся красный сигнал светофора. После нажатия на педаль тормоза автомобиль полностью остановился через 100 метров. Зная, что время торможения заняло 14 секунд, необходимо рассчитать соответствующее ускорение.

Для решения задачи можно сразу же воспользоваться одной из записанных выше формул:

Переведем начальную скорость автомобиля из км/ч в м/с, получаем:

v0 = 63*1000/3600 = 17,5 м/с2.

Источник

Формулы модуля ускорения для прямолинейного и криволинейного движения. Пример решения задачи

В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.

Что такое ускорение?

Вам будет интересно: Смоленский государственный институт искусств: факультеты, специальности, сроки обучения, документы для поступления

Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:

Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с2). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.

Движение по прямой и ускорение

Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.

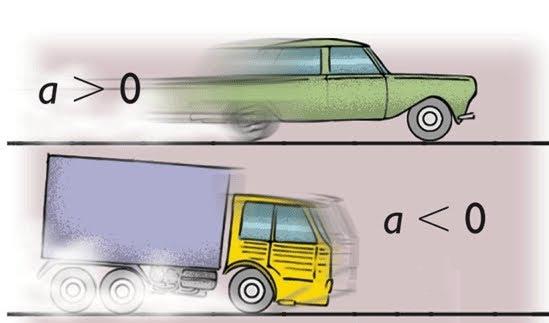
В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение. Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:

Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с2).

Полное ускорение и его компоненты при движении тела по кривой

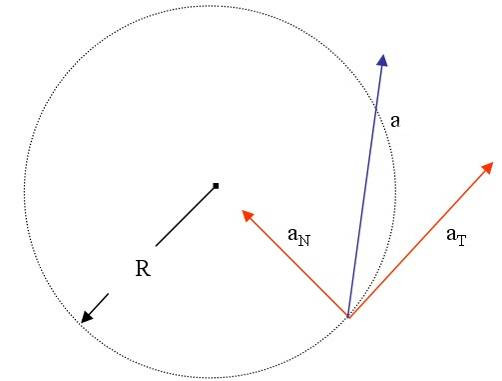
В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным at и нормальным an ускорениями. Для такого случая формула модуля ускорения точки принимает вид:

Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:

Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина at может быть равна нулю, что является справедливым для равномерного вращения тел.

Угловое ускорение

Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:

Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.

Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:

Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента at линейно возрастает при увеличении радиуса кривизны r.

Пример решения задачи

Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:

Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.

Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:

at = dv/dt = 6*t + 6*t2 = 6*3 + 6*9 = 76 м/с2.

Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с2).

Нормальная компонента вычисляется так:

an = v2/r = 1/r*(2 + 3*t2 + 2*t3)2 = 1/0,2*(2+27+54)2 = 34445 м/c2.

Теперь можно рассчитать полное ускорение. Оно будет равно:

a = √(at2 + an2) = √(76 2 + 34445 2) = 34445,1 м/с2.

То есть, полное ускорение практически полностью образовано нормальной компонентой.

Наконец, ускорение угловое определяется по формуле:

α = at/r = 76/0,2 = 380 рад/с2.

Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.

Источник

Прямолинейное равноускоренное движение. Формулы и решение задач

Одним из самых распространенных видов перемещения объектов в пространстве, с которым человек встречается повседневно, является равноускоренное прямолинейное движение. В 9 классе общеобразовательных школ в курсе физики изучают подробно этот вид движения. Рассмотрим его в статье.

Кинематические характеристики движения

Прежде чем приводить формулы, описывающие равноускоренное прямолинейное движение в физике, рассмотрим величины, которые его характеризуют.

Вам будет интересно: Методика ШТУР: расшифровка аббревиатуры, особенности проведения теста, итоговый анализ и результаты

Вам будет интересно: «Рубаха-парень»: значение в прошлом и сейчас

Путь S и скорость v являются переменными характеристиками при прямолинейном равноускоренном движении. Ускорение же является величиной постоянной.

Связь скорости и ускорения

Представим себе, что некоторый автомобиль движется по прямой дороге, не меняя свою скорость v0. Это движение называется равномерным. В какой-то момент времени водитель стал давить на педаль газа, и автомобиль начал увеличивать свою скорость, приобретя ускорение a. Если начинать отсчет времени с момента, когда автомобиль приобрел ненулевое ускорение, тогда уравнение зависимости скорости от времени примет вид:

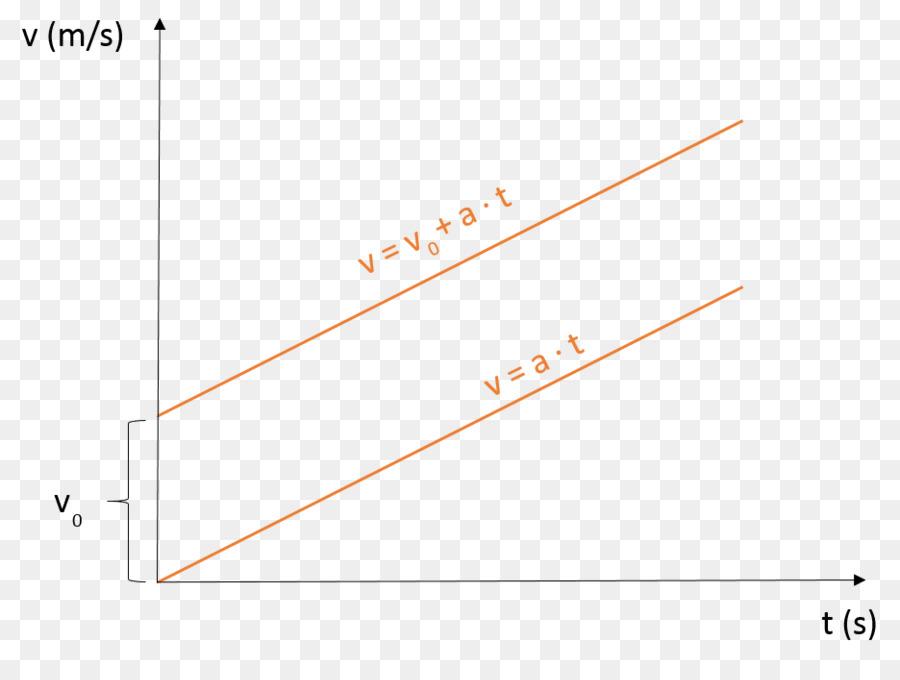
На рисунке показаны два графика. Отличие между ними заключается только в том, что верхний график соответствует скорости при наличии некоторого начального значения v0, а нижний описывает скорость равноускоренного прямолинейного движения, когда тело начало из состояния покоя ускоряться (например, стартующий автомобиль).

Отметим, если в примере выше водитель вместо педали газа нажал бы педаль тормоза, то движение торможения описывалось бы следующей формулой:

Этот вид движения называется прямолинейным равнозамедленным.

Формулы пройденного пути

На практике часто важно знать не только ускорение, но и значение пути, который за данный период времени проходит тело. В случае прямолинейного равноускоренного движения эта формула имеет следующий общий вид:

S = v0 * t + a * t2 / 2.

В случае торможения движущегося объекта выражение для пути примет вид:

В отличие от предыдущего случая здесь ускорение направлено против скорости движения, что приводит к обращению в ноль последней через некоторое время после начала торможения.

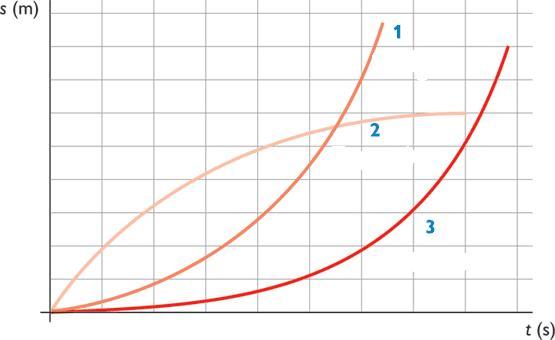
Не сложно догадаться, что графиками функций S(t) будут ветви параболы. На рисунке ниже представлены эти графики в схематическом виде.

Параболы 1 и 3 соответствуют ускоренному перемещению тела, парабола 2 описывает процесс торможения. Видно, что пройденный путь для 1 и 3 постоянно увеличивается, в то время как для 2 он выходит на некоторую постоянную величину. Последнее означает, что тело прекратило свое движение.

Далее в статье решим три разные задачи на использование приведенных формул.

Задача на определение времени движения

Автомобиль должен отвести пассажира из пункта A в пункт B. Расстояние между ними 30 км. Известно, что авто в течение 20 секунд движется с ускорением 1 м/с2. Затем его скорость не меняется. За какое время авто доставит пассажира в пункт B?

Расстояние, которое авто за 20 секунд пройдет, будет равно:

При этом скорость, которую он наберет за 20 секунд, равна:

Тогда искомое время движения t можно вычислить по следующей формуле:

Переведем все известные данные в систему СИ и подставим в записанное выражение. Получим ответ: t = 1510 секунд или приблизительно 25 минут.

Задача на расчет пути торможения

Теперь решим задачу на равнозамедленное движение. Предположим, что грузовой автомобиль двигался со скоростью 70 км/ч. Впереди водитель увидел красный сигнал светофора и начал останавливаться. Чему равен тормозной путь авто, если он остановился за 15 секунд.

Тормозной путь S можно рассчитать по следующей формуле:

Время торможения t и начальную скорость v0 мы знаем. Ускорение a можно найти из выражения для скорости, учитывая, что ее конечное значение равно нулю. Имеем:

Подставляя полученное выражение в уравнение, приходим к конечной формуле для пути S:

Подставляем значения из условия и записываем ответ: S = 145,8 метра.

Задача на определение скорости при свободном падении

Пожалуй, самым распространенным в природе прямолинейным равноускоренным движением является свободное падение тел в поле гравитации планет. Решим следующую задачу: тело с высоты 30 метров отпустили. Какую скорость будет оно иметь в момент падения на поверхность земли?

Искомую скорость можно рассчитать по формуле:

Время падения тела определим из соответствующего выражения для пути S:

Подставляем время t в формулу для v, получаем:

v = g * √(2 * S / g) = √(2 * S * g).

Значение пройденного телом пути S известно из условия, подставляем его в равенство, получаем: v = 24,26 м/с или около 87 км/ч.

Источник