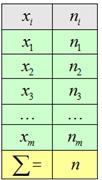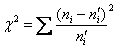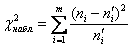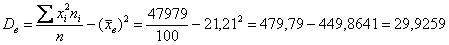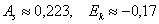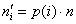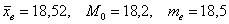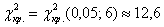Для чего и каким образом проводится проверка гипотезы нормального распределения
Проверка гипотезы о нормальном распределении
Перейти к онлайн решению своей задачи
Решение находим с помощью калькулятора.
Таблица для расчета показателей.
| xi | Кол-во, fi | xi·fi | Накопленная частота, S | (x- x )·f | (x- x ) 2 ·f | (x- x ) 3 ·f | Частота, fi/n |
| 5 | 15 | 75 | 15 | 114.45 | 873.25 | -6662.92 | 0.075 |
| 7 | 26 | 182 | 41 | 146.38 | 824.12 | -4639.79 | 0.13 |
| 9 | 25 | 225 | 66 | 90.75 | 329.42 | -1195.8 | 0.13 |
| 11 | 30 | 330 | 96 | 48.9 | 79.71 | -129.92 | 0.15 |
| 13 | 26 | 338 | 122 | 9.62 | 3.56 | 1.32 | 0.13 |
| 15 | 21 | 315 | 143 | 49.77 | 117.95 | 279.55 | 0.11 |
| 17 | 24 | 408 | 167 | 104.88 | 458.33 | 2002.88 | 0.12 |
| 19 | 20 | 380 | 187 | 127.4 | 811.54 | 5169.5 | 0.1 |
| 21 | 13 | 273 | 200 | 108.81 | 910.74 | 7622.89 | 0.065 |
| 200 | 2526 | 800.96 | 4408.62 | 2447.7 | 1 |
Пример 2. Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n = 200.
Решение.
Таблица для расчета показателей.
Мир статистических гипотез
В современном мире мы обладаем все большим и большим объемом данных о событиях, происходящих вокруг. Зачастую у нас появляются вопросы, на которые хотелось бы быстро ответить на основе имеющейся информации, для этого как нельзя лучше подходит процесс, связанный с проверкой статистических гипотез. Однако, многие считают, что это занятие подразумевает под собой большое число вычислений и в принципе довольно сложно для понимания. На самом деле, алгоритм проверки гипотез достаточно прост, а для осуществления расчетов с каждым годом появляется все больше и больше готовых инструментальных средств, не требующих от человека глубоких познаний в области. Далее я попытаюсь показать, что мало того, что процесс проверки гипотез может быть полезным, так и осуществляется достаточно быстро и без серьезных усилий.
Статистические гипотезы и области их применения
Проверка статистических гипотез является важнейшим классом задач математической статистики. С помощью данного инструмента можно подтвердить или отвергнуть предположение о свойствах случайной величины путем применения методов статистического анализа для элементов выборки. Если в предыдущем предложении какие-либо термины являются не совсем понятными, ниже можно найти пояснение на простом языке.
Для проверки статистических гипотез зачастую применяются статистические тесты, о которых будет рассказано далее.
Алгоритм проверки статистической гипотезы
В обобщенном виде алгоритм выглядит таким образом:
Формулировка основной (H0) и альтернативной (H1) гипотез
Выбор уровня значимости
Выбор статистического критерия
Определения правила принятия решения
Итоговое принятие решения на основе исходной выборки данных
Данные шаги являются унифицированными и схему можно использовать почти во всех случаях. Далее подробнее рассмотрим пример работы данного алгоритма на конкретных данных.
Пример проверки статистической гипотезы
Итак, как вы, наверное, догадались по вышеприведенным примерам, будем проверять гипотезу о том, что имеется существенное различие между числом созданных европейских AI-стартапов в 2019-м и 2020-м годах. Пример достаточно простой, чтобы было проще разобраться в ходе работы алгоритма.
Проверка гипотезы о законе распределения
Для данных 2019-го года проверим нормальность распределения.
H0: случайная величина распределена нормально
H1: случайная величина не распределена нормально
Пусть уровень значимости alpha = 0.05 (как и в 95-ти процентах статистических тестов). Определение уровня значимости достойно отдельного поста, так что не будем заострять на нем внимание.
Будет использован критерий Шапиро-Уилка.
,
,
,
;
Можно сравнить статистику W с критическим значением Wкрит. Критическое значение чаще всего приведено в готовых таблицах (по строкам/столбцам там отмечен объем выборки и уровень значимости, а на пересечении как раз-таки и лежит Wкрит.). Если W>Wкрит., то не отвергаем H0 и наоборот. Но это не очень удобно, поэтому чаще используется второй способ.
Разнообразие статистических критериев
Как мы увидели на примере, важным шагом в проверке статистической гипотезы является выбор критерия. В примере выше я использовала лишь два статистических критерия, но по факту их гораздо больше, так сказать, на все случаи жизни. Данные критерии важно знать и четко нужно осознавать, когда и какой можно применить. Многие из них направлены на сравнение центров распределений случайных величин, например, сравнение средних, медиан, равенство параметра распределения какому-либо числу и т. д. В основном они делятся на параметрические (знаем закон распределения случайной величины) и непараметрические.
Для вашего удобства внизу (рис. 3) приведена таблица с основными, с моей точки зрения, критериями сравнения центров распределения и их классификацией. Надеюсь, она будет вам полезна, ее можно дополнять и расширять по вашему желанию.
Для чего и каким образом проводится проверка гипотезы нормального распределения
1. Статистические гипотезы. Основные понятия.
2. Гипотезы о законе распределения.
3. Гипотезы о числовом значении генерального среднего и дисперсии.
1. Статистические гипотезы. Основные понятия.
В тех случаях, когда известен закон, но неизвестны значения его параметров (дисперсия или математическое ожидание) в конкретной ситуации, статистическую гипотезу называют параметрической.
Например, предположение об ожидаемом среднем доходе по акциям или разбросе дохода являются параметрическими гипотезами.
Когда закон распределения генеральной совокупности не известен, но есть основания предположить, каков его конкретный вид, выдвигаемые гипотезы о виде его распределения называются непараметрическими.
Например, можно выдвинуть гипотезу, что число дневных продаж в магазине или доход населения подчинены нормальному закону распределения.
По содержанию статистические гипотезы можно классифицировать:
1. Гипотезы о типе вероятностного закона распределения случайной величины, характеризующего явление или процесс.
2. Гипотезы об однородности двух или более обрабатываемых выборок. Изучаемое свойство исследуется с помощью двух или более генеральных совокупностей. Гипотеза в этом случае может заключаться в следующем: исследуемые выборочные характеристики различаются между собой статистически значимо или нет.
3. Гипотезы о свойствах числовых значений параметров исследуемой генеральной совокупности. Больше ли значения параметров некоторого заданного номинала или меньше и т.д.
4. Гипотезы о вероятностной зависимости двух или более признаков, характеризующих различные свойства рассматриваемого явления или процесса. При этом определяется характер этой зависимости.
Гипотезы бывают простые (содержащие одно предположение) и сложные (содержащие несколько предположений).
Под статистическим критерием понимают однозначно определенное правило, устанавливающее условие, при котором проверяемая гипотеза отвергается либо не отвергается.
Увеличение числа заболевших некоторым заболеванием дает возможность выдвинуть гипотезу о наличии эпидемии. Для сравнения доли заболевших в обычных и экстремальных условиях используются статистические данные, на основании которых делается вывод о том, является ли данное массовое заболевание эпидемией. Предполагается, что существует некоторый критерий- уровень доли заболевших, критический для этого заболевания, который устанавливается по ранее имевшимся случаям.
Различают три вида критериев:
Проверка параметрических гипотез проводится на основе критериев значимости., а непараметрических- критериев согласия.
Задача проверки статистических гипотез сводится к исследованию генеральной совокупности по выборке. Множество возможных значений элементов выборки может быть разделено на два непересекающихся подмножества- критическую область и область принятия гипотезы.
Областью принятия гипотезы или областью допустимых значений Iдоп называют совокупность значений критерия, при которых эту гипотезу принимают.
Критической областью Iкр называют множество значений критерия, при котором гипотезу отвергают.
Наблюдаемые значения критерия (статистика) Kнабл называют такое значение критерия, которое находится по данным выборки.
С помощью уровня значимости определяются границы критической области.
Основной принцип проверки статистических гипотез состоит в следующем: если наблюдаемое значение статистики критерия попадает (не попадает) в критическую область, то гипотеза H0 отвергается (принимается), а гипотеза H1 принимается (отвергается) в качестве одного из возможных решений с формулировкой «гипотеза H0 противоречит (не противоречит) выборочным данным на уровне значимости ».
В зависимости от содержания альтернативной гипотезы осуществляется выбор критической области: левосторонней, правосторонней, двусторонней. Если смысл исследования заключается в доказательстве конкретного изменения наблюдаемого параметра (его уменьшения или увеличения), то говорят об односторонней критической области. Если смысл исследования- выявить различия в изучаемых параметрах, но характер их отклонения от контрольных (или теоретических) не известен, то говорят о двусторонней критической области.
Однако, принятие той или иной гипотезы не дает оснований утверждать, что она верна. Результат проверки статистической гипотезы лишь устанавливают на определенном уровне значимости ее соответствие (несоответствие) результатам эксперимента.
При проверке статистических гипотез возможны следующие ошибки:
2. Отвергнута правильная альтернативная гипотеза H1 и принята неправильная нулевая гипотеза H0 — ошибка второго рода.
Можно доказать, что с уменьшением ошибок первого рода одновременно увеличиваются ошибки второго рода и наоборот. Поэтому, на практике пытаются подбирать значения параметров и опытным путем в целях минимизации суммарного эффекта от возможных ошибок. При принятии управленческих решений для одновременного уменьшения ошибок первого и второго рода самым действенным средством является увеличение объема выборки, что согласуется с законом больших чисел.
На бытовом уровне ошибки второго рода могут иметь более трагические последствия, чем ошибки первого рода.
2. Гипотеза о законе распределения. Критерий согласия Пирсона ( X 2 -критерий).
Критериями согласия называют критерии, в которых гипотеза определяет закон распределения либо полностью, либо с точностью до небольшого числа параметров.
Причины расхождения результатов эксперимента и теоретических характеристик могут быть вызваны малым объемом выборки, неудачным способом группировки наблюдений, ошибками в выборе гипотезы о виде распределения генеральной совокупности и др.
Рассмотрим универсальный критерий согласия Пирсона. Проверка гипотезы о том, что эмпирическая частота мало отличается от соответствующей теоретической частоты, осуществляется с помощью величины X 2 — меры расхождения между ними.
Для произвольной выборки, когда распределение непрерывно или число различных вариант велико, все пространство наблюдаемых вариант делят на конечное число непересекающихся областей, в каждой из которых подсчитывают наблюдаемую частоту и теоретическую вероятность.
Для применения критерия согласия Пирсона необходимо:
13. Гипотеза о законе распределения генеральной совокупности.
Критерий согласия Пирсона
Итак, после разгрома двух десятков задач ставим вишенку на торт статистических гипотез, а именно разбираем важнейшую гипотезу о виде (законе) распределения и распространённые тематические примеры.
Рассмотрим генеральную совокупность, распределение которой неизвестно. Однако есть основание полагать, что она распределена по некоторому закону 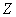
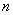
И нам требуется на уровне значимости 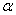
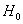
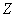
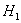
Как проверить эту гипотезу? Постараюсь объяснить кратко. Как вы знаете, выборочные данные группируются в дискретный или интервальный вариационный ряд с вариантами 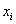
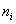
Поскольку эти данные взяты из практического опыта, то выборочный вариационный ряд называют эмпирическим рядом, а частоты 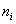
Далее строятся графики, рассчитываются выборочные характеристики (выборочная средняя 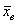
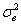
На основе некоторых выборочных характеристик по специальным формулам, которые зависят от проверяемого закона 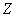
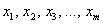
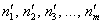
И возникает вопрос: значимо или незначимо различие между эмпирическими 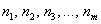
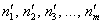
Для ответа на это вопрос рассматривают различные статистические критерии, которые называют критериями согласия, и наиболее популярный из них разработал Карл Пирсон:
При достаточно большом 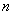
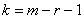
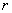
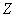
…всем понятно, почему величина 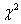
Далее строится правосторонняя критическая область: 
Критическое значение 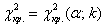
Наблюдаемое значение критерия рассчитывается по эмпирическим и найденным теоретическим частотам:
Если 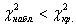
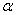
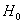
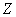
Если 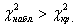
Обратите внимание на формулировку, которую я выделил жирным цветом – такая формулировка напоминает нам о том, что принятие статистической гипотезы ещё не означает её истинность, поскольку существует 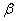
И, наконец, бараны коровы, которые нас уже заждались. Реалистичность фактических данных оставлю на совести автора методички сельскохозяйственной академии:
По результатам выборочного исследования найдено распределение средних удоев молока в фермерском хозяйстве (литров) от одной коровы за день:
На уровне значимости 0,05 проверить гипотезу о том, что генеральная совокупность (средний удой коров всей фермы) распределена нормально. Построить гистограмму частот и теоретическую кривую.
…если не любите молоко, то пусть это будет чай, сок, пиво или какой-то другой напиток, который вам нравится 🙂 Чтобы было интереснее исследовать эту волшебную ферму.
Решение: на уровне значимости 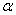
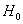
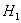
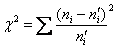
Эмпирические частоты известны из предложенного интервального ряда, и осталось найти теоретические. Для этого нужно вычислить выборочную среднюю 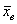
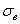
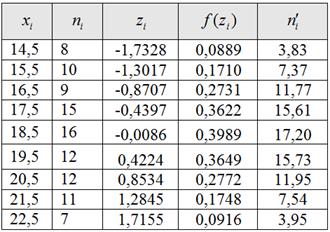
Выберем в качестве вариант 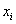
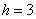
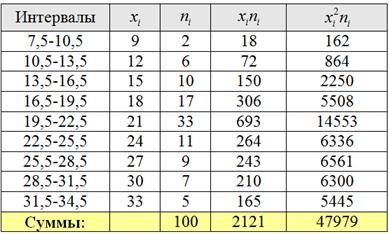
Внимание! Если вы не понимаете, как заполнять эту таблицу, или не знаете, как это сделать быстро, то обязательно обратитесь к Примеру 16, там есть все объяснения и видео!
Вычислим выборочную среднюю:
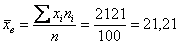
Выборочную дисперсию вычислим по формуле:
И выборочное стандартное отклонение:
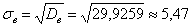
По причине большого объёма выборки его исправлением можно пренебречь.
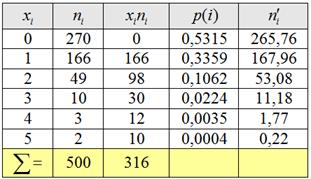
Теоретические частоты рассчитываются по формуле: 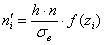
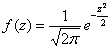
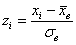
Входные данные известны: 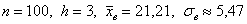
Все вычисления удобно проводить в Экселе и на всякий случай я распишу одну строчку:
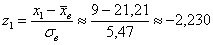
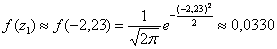
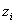
И, наконец, теоретическая частота: 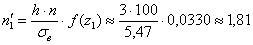
Надеюсь, на данный момент уже все умеют протягивать (копировать) формулы по образцу, а если нет, то я всё равно научу 🙂 Решил таки записать отдельный ролик, хотя особой технической новизны тут нет:

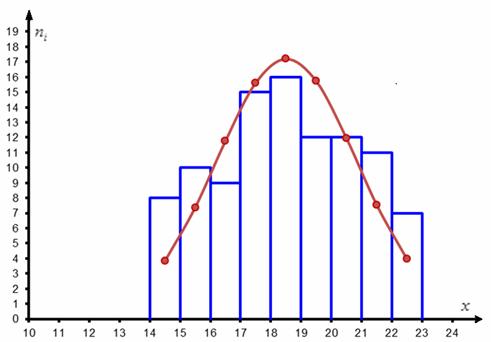
Построим гистограмму эмпирических частот и теоретическую кривую, которая проходит через точки 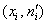
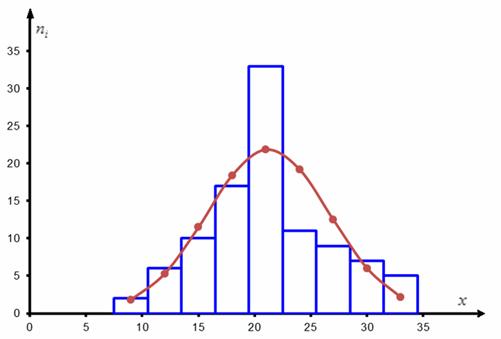
О технике построения гистограммы в MS Excel я рассказывал на уроке об интервальном ряде распределения, вот нужный ролик на Ютубе, и далее через правый клик к ней добавляется нормальная кривая. Эта кривая построена на основе выборочных данных (выборочной средней и стандартного отклонения) и наилучшим образом приближает гистограмму. Дальнейшая задача состоит в том, чтобы оценить, насколько ЗНАЧИМО отличаются эмпирические частоты (ступеньки гистограммы) от соответствующих теоретических частот (уровень коричневых точек).
Но перед тем, как сравнивать теоретические и эмпирические частоты, следует объединить интервалы с малыми (меньше пяти) частотами. В данном случае объединяем два первых и два последних интервала, для этого суммируем частоты, обведённые красным цветом, и получаем оранжевые результаты: 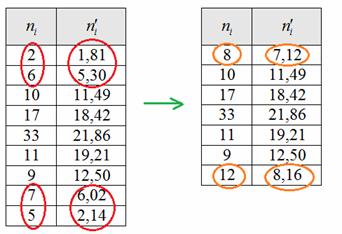
Это нужно для того, чтобы сгладить неоправданно большое расхождением между малыми частотами по краям выборки. Действие не обязательное, но крайне желательное, ибо студентов на моей памяти часто заставляли переделывать задание.
Найдём критическое значение 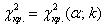
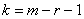
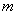
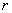
Так как мы объединяли интервалы, то теперь их не девять, а 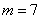
У нормального закона мы оцениваем 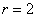
Пояснение: 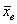
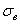
Таким образом, 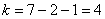
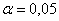
Это значение можно найти по таблице критических значений распределения хи-квадрат или с помощью Калькулятора (Пункт 11б).
При 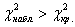
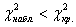

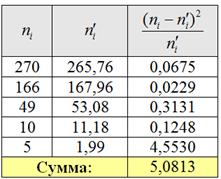
Вычислим наблюдаемое значение критерия 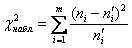
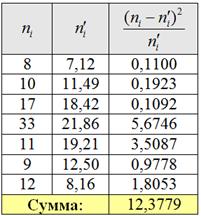
На всякий пожарный пример расчёта: 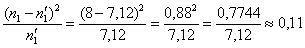
В нижней строке таблицы у нас получилось готовое значение 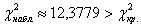
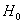
Иными словами различие между эмпирическими и теоретическими частотами статистически значимо и вряд ли объяснимо случайными факторами.
Ответ: на уровне значимости 0,05 гипотезу о нормальном распределении отвергаем
В чём может быть причина? Ведь по теореме Ляпунова большинство коров не оказывает практически никакого влияния на удой других коров, и поэтому распределение ген. совокупности должно быть близкО к нормальному.
Причины могут быть разными. Например, неоднородный состав совокупности (коровы разной породы), или на ферме есть VIP-хлев, где коровы получают улучшенное питание 🙂 А может быть, некоторые коровы больны и как раз оказывают существенное влияние на остальных, в связи с чем нарушается условие теоремы Ляпунова.
Интересно отметить, что при уменьшении уровня значимости до 0,01 критическое значение 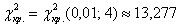
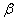
И, конечно, в случае сомнений имеет смысл увеличить объём выборки, чтобы провести повторное исследование.
Рассмотренная задача может встретиться в более простой или более сложной формулировке. В версии-«лайт» вам предложат готовые теоретические частоты, где остаётся только проверить гипотезу. Продвинутое же условие звучит примерно так:
На основании исследования выборки выдвинуть гипотезу о законе распределения генеральной совокупности
То есть, здесь не говорится о том, что предполагаемый закон нормальный (или какой-то другой) – этот вопрос вам предлагается проанализировать самостоятельно.
Каким образом это можно сделать?
Во-первых, гипотезу можно выдвинуть априорно, даже не исследуя выборку, и зависеть она будет от содержания задачи. Так, для коров используем упомянутую выше теорему Ляпунова: если каждый объект совокупности оказывает несущественное влияние на всю совокупность, то её распределение близкО к нормальному. Если речь идёт о погрешностях округления, то распределены они обычно равномерно. Если распадаются радиоактивные изотопы, то, скорее всего, по экспоненциальному закону. И так далее.
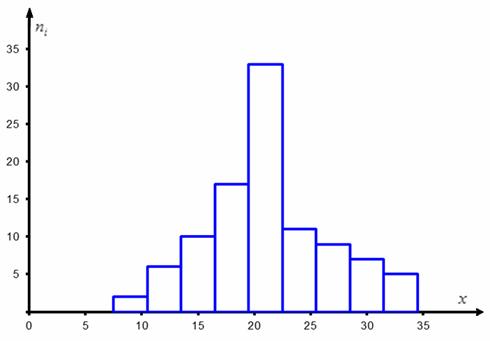
Но по условию, требуют опираться на выборочные данные, и здесь есть сразу несколько признаков, чтобы «вычислить» этот закон. Самый простой и наглядный способ – графический. Грубо говоря, чертим и смотрим. Интервальный вариационный ряд чаще всего изображают гистограммой, возвращаемся к нашим коровам:
Построенная гистограмма по форме напоминает колоколообразный график плотности нормального распределения, и это является веской причиной предположить, что генеральная совокупность распределена нормально. Да, здесь есть слишком высокий средний столбик, но, возможно, это просто случайность выборки.
Если столбики примерно одинаковы по высоте, то предполагаем, что генеральная совокупность распределена равномерно. Для показательного распределения тоже будет своя, характерная гистограмма.
Следующие признаки аналитические, приведу их для нормального распределения:
1) У нормального распределения математическое ожидание совпадает с модой и медианой. В нашем случае соответствующие выборочные показатели весьма близкИ друг к другу (матожидание оценивается выборочной средней):
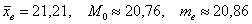

Желающие могут рассчитать моду и медиану самостоятельно. Впрочем, желающими часто становятся поневоле, поскольку задача, которую мы рассматриваем, нередко идёт в комплексе со всеми этими заданиями.
2) Выполнение правила «трёх» сигм. Практически все значения нормальной случайной величины находятся в интервале 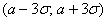
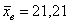
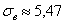
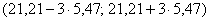
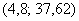
3) Коэффициенты асимметрии и эксцесса нормального распределения равны нулю. В нашем случае эти характеристики не сказать что сильно, но довольно близкИ к нулю:
На практике в исследование желательно включить все пункты за исключением, возможно, третьего (т.к. асимметрию и эксцесс рассчитывают далеко не всегда).
Следует отметить, что перечисленные выше предпосылки ещё не означают, что распределение нормально или то, что соответствующая гипотеза будет принята. В чём мы недавно и убедились.
И теперь настал момент продолжить решение нашего «экзаменационного» задания:
Если вы не прорешали предыдущие пункты, то настоятельно рекомендую это сделать, ну или просто взять готовые числа из образца:
6) По найденным характеристикам сделать вывод о законе эмпирического ряда распределения.
7) Построить нормальную кривую по опытным данным на графике гистограммы.
8) Произвести оценку степени близости теоретического распределения эмпирическому ряду с помощью критерия согласия Пирсона на уровне значимости 0,05.
Как видите, Пункт 6 как раз на обоснование предполагаемого закона распределения. Краткое решение в конце этого урока.
И, конечно же, ещё одна задача, передаю привет студентам Университета путей сообщения:
В результате проверки 500 контейнеров со стеклянными изделиями установлено, что число повреждённых изделий 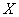

( 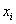
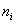
С помощью критерия согласия Пирсона на уровне значимости 0,05 проверить гипотезу о том, что случайная величина 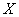
…здесь тоже представьте изделия по своему интересу 🙂
Все числа уже забиты в макет, придерживайтесь следующего алгоритма:
1) Находим выборочную среднюю 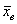
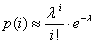
2) Находим значения 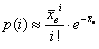
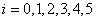
3) Находим теоретические частоты
4) Находим критическое значение 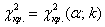
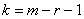
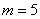
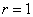
5) Рассчитываем наблюдаемое значение критерия 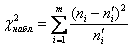
Примерный образец чистового оформления задачи в конце урока.
Помимо разобранных примеров, в задачнике В. Е. Гмурмана можно найти аналогичные задачи для биномиального, равномерного и показательного распределения, но лично в моей практике они почти не встречались.
Желаю успехов и до скорых встреч!
Пример 20. Решение (продолжение):
6) Проанализируем полученные результаты:
Форма гистограммы похожа на нормальную кривую.
Выборочная средняя, мода и медиана достаточно близкИ друг другу:
Построим интервал 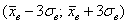
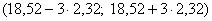
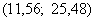
Асимметрия практически равна нулю 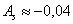
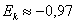
Перечисленные признаки позволяют предположить, что генеральная совокупность распределена нормально.
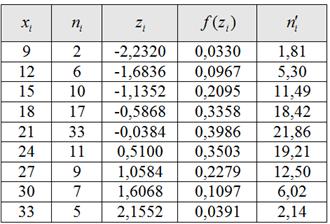
7) Найдём теоретические частоты: 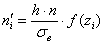
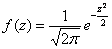
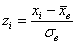
в данной задаче 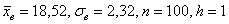
Построим гистограмму частот и теоретическую кривую:
8) Проверим гипотезу 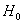
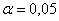
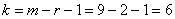
При 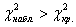
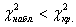
Вычислим наблюдаемое значение критерия 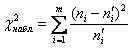
В результате: 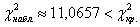
Пример 54. Решение: проверим гипотезу 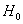
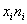
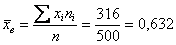
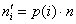
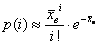
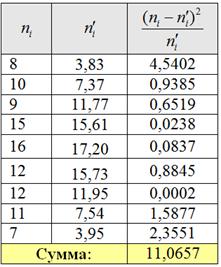
Вычисления сведём в таблицу:
Объединяем две последние варианты ввиду их малых частот и находим критическое значение для уровня значимости 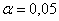
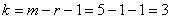
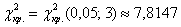
Вычислим наблюдаемое значение критерия 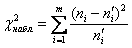
Таким образом, 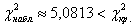
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5