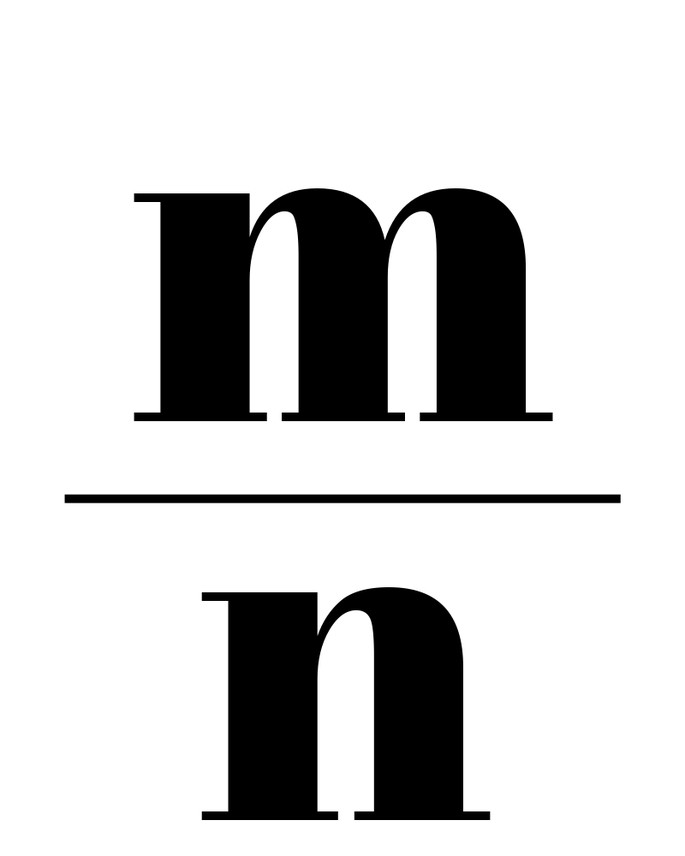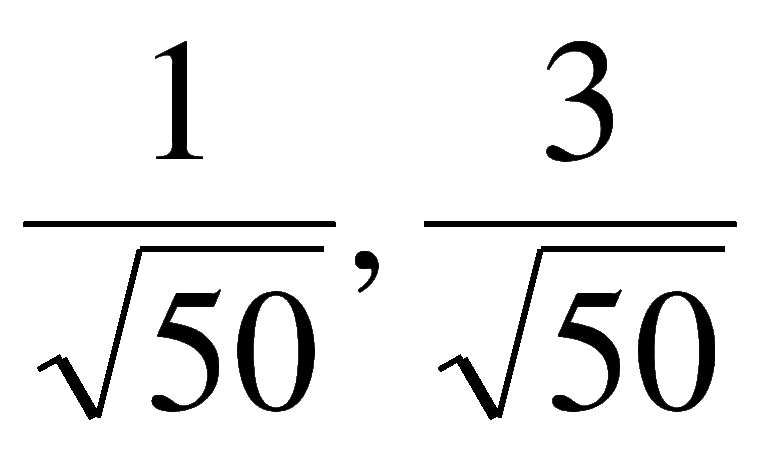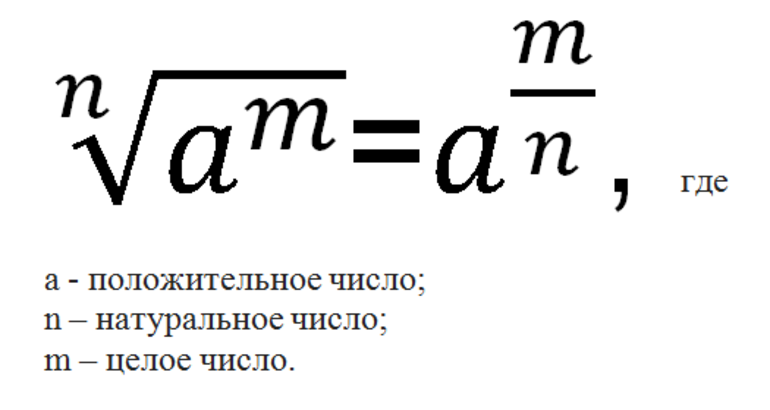Для чего иррациональные числа
Иррациональные числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение иррациональных чисел
Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби:
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.
Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.
Примеры иррациональных чисел:
Множество иррациональных чисел договорились обозначать латинской буквой I.
Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.
Свойства иррациональных чисел
Какие числа являются иррациональными мы уже поняли, но это еще не все. Есть еще важная тема для изучения: их основные свойства.
Свойства иррациональных чисел:
Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.
Определение рациональных чисел
А теперь наоборот: рассмотрим противоположное заданной теме определение.
Рациональное число — это такое число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или нуля. Если число можно получить делением двух целых чисел — это число точно рациональное.
Рациональные числа — это те, которые можно представить в виде:
где числитель m — целое число, а знаменатель n — натуральное число.
Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Множество рациональных чисел принято обозначать латинской буквой Q.
Примеры рациональных чисел:
У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.
Основные свойства действий с рациональными числами
Буддийский физмат: как гёделевская неполнота и иррациональные числа породили нашу Вселенную
Каждый человек в определенный момент своей жизни начинает задаваться вопросами: «Почему существует Вселенная?», «Что такое время?», «Что было до Большого Взрыва?».
Со мной это произошло несколько лет тому назад. Я стал искать ответы на эти вопросы, пытаясь найти их везде: в научно-популярных книгах по физике, в древнегреческой и древнеиндийской философии, в популярных и эзотерических религиях. В каждом из этих направлений человеческой мысли я не находил окончательной истины, но находил одну из её бесконечных граней.
Наш ум анализирует поток сырых сенсорных данных от органов чувств: он различает разные цвета, звуки, запахи и конструирует из них цельную картину сознания. Именно из-за этих базовых свойств нашего ума: различения базовых частиц восприятия и конструирования из них абстракций, мы видим внешний мир как набор отношений между абстрактными объектами.
Пустота материи, пространства и времени
Если мы рассмотрим любые предметы, которые мы считаем материальными, с точки зрения буддийской доктрины пустоты, то они окажутся иллюзией и «исчезнут». Виктор Пелевин в своём известном романе «Чапаев и Пустота» рассказывал метафорическую историю про Будду, указывавшего на разные предметы своим мизинцем, после чего эти предметы тотчас исчезали.
Наука о пустоте
Вот её определение из Википедии:
Если однажды мы встретимся с представителями внеземных цивилизаций, то можно с уверенностью сказать, что и в их математическом аппарате дважды два будет равно четырем. Конечно, они будут обозначать цифры и операции другими символами, но суть будет та же самая. С помощью математических выражений мы сможем найти и другие сходства с инопланетной наукой: у них ведь будут те же самые, что и у нас, законы физики, химии и частично даже биологии.
Но что, если мы встретимся с существами из вообще другой Вселенной с отличными от наших законами физики? Какие точки соприкосновения с ними мы сможем найти? Очевидно, что единственной общей вещью между нами и иновселянами будет математика. Ведь даже несмотря на отличные от наших законов физики, законы математики в их Вселенной будут такими же как и у нас. Невозможно существование какой-то иной математики. Математика никак не зависит от времени, пространства и любых других свойств той Вселенной, в которой мы существуем. Ведь если подумать, то даже до Большого Взрыва утверждение «дважды два равно четыре» должно было быть верным.
Рассуждая схожим образом, древнегреческий философ Платон пришел к выводу, что математика обладает независимым бытием и существует в неком нематериальном «мире форм». В доказательство своему утверждению Платон приводил правильные многогранники, позже в его честь названные платоновыми телами.
Платоновы тела
Рождение Вселенной
Мы подошли к самой красивой части «буддийского физмата»: гипотезе рождения Вселенной. Эта часть содержит достаточно много непростой метафизики, но начинается она с единственного постулата: все вещи существуют симметрично относительно друг друга. Я употребляю слово «существует», а не «возникает», потому что возникновение предполагает некий процесс во времени, а в мире абсолютных форм нет времени, оно появляется позже.
Одной из таких структур становятся иррациональные и трансцендентные числа, то есть числа не представимые в виде целочисленной дроби или корня уравнения. Количество цифр после запятой у таких чисел бесконечно. Самым известным трансцендентным числом является число π:
3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989.
Нетривиальные нули дзета-функции Римана (их мнимые части) соответствуют собственным значениям некоторого эрмитового оператора (неограниченного самосопряжённого оператора в гильбертовом пространстве).
Оказалось, что квантовый хаос прекрасно описывается распределением нетривиальных нолей функции Римана:
Связь статистики нетривиальных нулей дзета-функции Римана (синие точки — первые 105 нетривиальных нулей) с квантовым хаосом (непрерывная линия описывает двухточечную корреляционную функцию случайной матрицы типа ГУА)
Британский научно-популярный писатель Джон Дербишир задавался вопросом на этот счёт:
Нетривиальные нули дзета-функции Римана появились при исследовании распределения простых чисел. Собственные значения случайных эрмитовых матриц появились при исследовании поведения систем субатомных частиц, подчиняющихся законам квантовой механики. Скажите, пожалуйста, что вообще может быть общего между простыми числами и поведением субатомных частиц?
Если бы он был знаком с «буддийским физматом», он бы знал ответ! Более того, «буддийский физмат» проливает свет и на то, почему наш мир на микроуровне, изучаемом квантовой механикой, кажется случайным, а на макроуровне абсолютно стабилен. Каждое следующее простое число случайно и невычислимо по точной формуле, но их распределение строго подчинено дзета-функции Римана. А каждая следующая цифра после запятой в иррациональном числе тоже абсолютно случайна: 
, но их общее количество на большом масштабе абсолютно стабильно: например, в первом миллионе цифр после запятой числа Пи 99959 нулей, 99758 единиц, 100026 двоек, 100229 троек, 100230 четвёрок, 100359 пятёрок, 99548 шестёрок, 99800 семёрок, 99985 восьмёрок и 100106 девяток. Получается, простые и иррациональные числа, прямо как наша Вселенная, строго детерминированы математикой, но кажутся случайными на микромасштабах.
Вывод
История открытия
Одни учёные считают, что иррациональные числа были открыты Пифагором. Другие полагают, что существование таких величин было выявлено пифагорейцами в V веке до нашей эры. Третьи выдвигают версию, что открытие принадлежит древним учёным Азии.
Несмотря на то что возникновение нового типа чисел связывают с именем Пифагора, сам великий учёный этих величин не признавал. Математик основывал свои труды на рациональности значений, а потому их иные виды были неприменимы к его теориям. Из-за огромного авторитета учёного иррациональные значения стали использоваться в науке только после его смерти.
Аристотель доказал иррациональность квадратного корня из 2. Теодор из Кирены привёл подобные доказательства в отношении корня из 3, 5 и так далее. Есть версия, что даже термины для соответствующей теории ввёл этот математик. Его ученик Теэтет на основании указанных данных создал общее учение об иррациональности. Полная теория иррациональных количественных значений Эвклид изложил в пятой книге «Начал».
Понятие и характеристика
Огромным прорывом в математической науке стали числа, которые называются иррациональными. Какие-либо ограничения, связанные с целыми величинами или обыкновенными дробями, были сняты. Люди получили возможность открывать и даже изобретать новые количественные значения.
Иррациональным считается вещественное число, не являющееся рациональным. Оно не может быть представлено в виде арифметической дроби n/m, где числитель и знаменатель являются целыми величинами, а n не равно 0. Также подобные значения невозможно точно выразить целой величиной. Это значит, что иррациональные числа всегда выглядят, как бесконечные непериодические десятичные дроби. Для их обозначения применяют радикалы или специальные буквы, например, е, π. Множество чисел обозначается заглавной буквой в полужирном начертании без заливки.
В геометрии оно представляется в качестве отрезка, длина которого несоизмерима с единичной. Об этой несоизмеримости упоминали и древние математики. Они установили, что диагональ квадрата не имеет общей меры с его стороной, что равносильно иррациональности корня из 2.
Не всякая величина из множества значений, не относящихся к рациональным, так известна, как число π. В школьной программе его часто определяют, как 3,14, но истинный показатель π значительно ближе к 3. Следует отметить, что даже известная длинная десятичная дробь является лишь приближённым вариантом, поскольку указанное число нельзя точно установить. Дробь, которую используют для этого, бесконечна, а цифры в ней распределяются без какой-либо закономерности.
Самыми известными примерами таких иррациональных чисел являются:
Математиками составлены специальные таблицы величин, не являющихся рациональными. Но так как множество бесконечно, определить тип значения по данным таблицам довольно сложно.
Зачастую понять, что число иррационально, можно по его соответствию одному из перечисленных признаков:
Но в ряде случаев установить иррациональность значения возможно только посредством доказательства. К примеру, школьникам часто дают задание доказать, что число log3 4 не относится к рациональным.
Отличительные качества
Значения, которые нельзя выразить дробью, существенно отличаются от других чисел. К их уникальным свойствам относятся следующие:
Виды преобразования выражений
Иррациональные выражения содержат операцию извлечения корня. Это особые записи, состоящие из радикалов и знаков алгебраических действий.
Во время преобразования таких выражений нельзя допускать сужения области допустимых значений. С ними разрешается проводить любые из основных тождественных преобразований:
В основе подобного упрощения выражений лежат действия, общие для всех количественных значений. Поэтому в процессе преобразования этих записей необходимо сохранять установленный порядок выполнения действий.
Замена исходной записи
Подкоренное выражение можно заменить тождественно равным, то есть математической записью, значение которой будет равно исходному. Следует учитывать, что равенство должно соблюдаться при любых допустимых значениях переменных, которые входят в состав обоих выражений.
Это утверждение основывается на единственности корня из числа. Иными словами, нет значения, которое, отличаясь от исходной величины, сохраняло бы равенство с нею.
Использование свойств корней
Для упрощения сложных выражений часто применяются свойства корней, к примеру, перемножение их степеней. Делать это необходимо в соответствии со специальными формулами.
Особое внимание при работе следует обращать на отрицательные числа и выражения с переменными. В ряде случаев для применения формул такие значения сначала придётся привести к тождественно равным, которые подойдут для дальнейшего использования свойств корней.
Внесение множителя под знак корня — это преобразование произведения, в котором лишь один из множителей находится под знаком радикала со степенью, выраженной натуральным числом. После замены выражения под корнем будут находиться все множители, составляющие произведение, но оно останется равным исходному.
Обратным изменением является вынесение множителя из-под радикала. Его используют в случаях, когда степень корня равна степени множителя под радикалом. В таких ситуациях указанный множитель можно извлечь и тем самым упростить выражение.
Изменение дробей
Иррациональные математические записи могут содержать дроби с радикалами в делимом или делителе. С ними разрешается проводить любые действия, относящиеся к основным преобразованиям дробных чисел:
Избавление от иррациональности в знаменателе
Освобождение от иррациональности в знаменателе представляет собой преобразование дроби путём её замены на тождественно равную с делителем, не содержащим корней и степеней. Для этого необходимо последовательно провести два действия:
Переход к степеням
Переход от радикалов к степеням осуществляется на основе равенства, давшего определение степени, которая имеет рациональный показатель. При этом используется следующая формула:
Если же величина под радикалом отрицательная или там находится выражение с переменными, то перед использованием формулы подкоренное значение необходимо преобразовать. Для этого следует применять свойства степеней.
Математические действия
Иррациональные выражения записывают друг за другом с сохранением знаков и лишь после этого складывают или вычитают. Иногда их преобразуют в подобные, то есть имеющие одинаковые подкоренные значения, а затем проводят арифметические действия.
Чтобы найти произведение выражений с одинаковыми радикалами, умножают значения, находящиеся под знаком корня. Полученный результат вносится под корень изначальных выражений.
При делении степени корней делимого и делителя также должны быть равны. Если это условие соблюдено, то первое выражение делится на второе, после чего итог действия записывается под исходный знак радикала.
Правила сравнения
Иногда для решения математических задач необходимо провести сравнение иррациональных значений. При этом необходимо руководствоваться следующими правилами:
Для возведения иррациональной величины в степень необходимо возвести в неё значение под радикалом. Если величина корня равна степени, то в итоге число или выражение выносится из-под корня неизменным, поскольку возникают взаимно сокращающиеся действия.
Если иррациональное выражение находится под корнем, то для его извлечения показатели радикалов умножают. Этот метод позволяет упрощать извлечение корней четвёртой, шестой, восьмой, девятой степени.
Иррациональные числа можно узнать по специальным буквам, используемым для их обозначения, или по написанию в виде десятичных дробей, не имеющих окончания. Выражения этого типа легко отличить по наличию радикала. С подобными значениями проводят те же действия, что и с другими вещественными числами. Их можно умножить, сложить, сравнить и так далее.
Для чего иррациональные числа
Множество иррациональных чисел обычно обозначается заглавной латинской буквой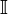 
в полужирном начертании без заливки. Таким образом: 
, т.е. множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.
О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа 
.
Свойства
Примеры
Примеры доказательства иррациональности
Корень из 2
Допустим противное: 
рационален, то есть представляется в виде несократимой дроби 
, где 
— целое число, а 
— натуральное число. Возведём предполагаемое равенство в квадрат:
.
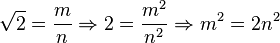
Отсюда следует, что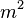 
чётно, значит, чётно и . Пускай 
, где 
целое. Тогда
Следовательно, 
чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число.
Двоичный логарифм числа 3
Допустим противное: 
рационален, то есть представляется в виде дроби , где и — целые числа. Поскольку 0″ src=»http://upload.wikimedia.org/math/d/1/3/d1351d4222403731e31419faebbe54bc.png» />, и могут быть выбраны положительными. Тогда
Но 
чётно, а 
нечётно. Получаем противоречие.
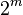
История
Концепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (ок. 750 г. до н. э. — ок. 690 г. до н. э.) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены.
Первое доказательство существования иррациональных чисел обычно приписывается Гиппасу из Метапонта (ок. 500 гг. до н. э.), пифагорейцу, который нашёл это доказательство, изучая длины сторон пентаграммы. Во времена пифагорейцев считалось, что существует единая единица длины, достаточно малая и неделимая, которая целое число раз входит в любой отрезок. Однако Гиппас обосновал, что не существует единой единицы длины, поскольку предположение о её существовании приводит к противоречию. Он показал, что если гипотенуза равнобедренного прямоугольного треугольника содержит целое число единичных отрезков, то это число должно быть одновременно и четным, и нечетным. Доказательство выглядело следующим образом:
Греческие математики назвали это отношение несоизмеримых величин алогос (невыразимым), однако согласно легендам не воздали Гиппасу должного уважения. Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям». Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.
Феодор Киренский доказал иррациональность корней натуральных чисел до 17 (исключая, естественно, точные квадраты — 1, 4, 9 и 16), но остановился на этом, так как имевшаяся в его инструментарии алгебра не позволяла доказать иррациональность квадратного корня из 17. По поводу того, каким могло быть это доказательство, историками математики было высказано несколько различных предположений. Согласно наиболее правдоподобному предположению Жана Итара (1961), оно было основано на пифагорейской теории чётных и нечётных чисел, в том числе — на теореме о том, что нечётное квадратное число за вычетом единицы делится на восемь треугольных чисел.
Позже Евдокс Книдский (410 или 408 г. до н. э. — 355 или 347 г. до н. э.) развил теорию пропорций, которая принимала во внимание как рациональные, так и иррациональные отношения. Это послужило основанием для понимания фундаментальной сути иррациональных чисел. Величина стала считаться не числом, но обозначением сущностей, таких как отрезки прямых, углы, площади, объёмы, промежутки времени — сущностей, которые могут меняться непрерывно (в современном понимании этого слова). Величины были противопоставлены числам, которые могут меняться лишь «прыжками» от одного числа к соседнему, например, с 4 на 5. Числа составляются из наименьшей неделимой величины, в то время как величины можно уменьшать бесконечно.
Поскольку никакое количественное значение не сопоставлялось величине, Евдокс смог охватить и соизмеримые, и несоизмеримые величины при определении дроби как отношения двух величин, и пропорции как равенства двух дробей. Убрав из уравнений количественные значения (числа), он избежал ловушки, состоящей в необходимости назвать иррациональную величину числом. Теория Евдокса позволила греческим математикам совершить невероятный прогресс в геометрии, предоставив им необходимое логическое обоснование для работы с несоизмеримыми величинами. «Книга 10 Элементов» Евклида посвящена классификации иррациональных величин.
Средние века
Средние века ознаменовались принятием таких понятий как ноль, отрицательные числа, целые и дробные числа, сперва индийскими, затем китайскими математиками. Позже присоединились арабские математики, которые первыми стали считать отрицательные числа алгебраическими объектами (наряду и на равных правах с положительными числами), что позволило развить дисциплину, ныне называемую алгеброй.
Арабские математики соединили древнегреческие понятия «числа» и «величины» в единую, более общую идею вещественных чисел. Они критически относились к представлениям Евклида об отношениях, в противовес ей они развили теорию отношений произвольных величин и расширили понятие числа до отношений непрерывных величин. В своих комментариях на Книгу 10 Элементов Евклида, персидский математик Аль Махани (ок 800 гг. н. э.) исследовал и классифицировал квадратичные иррациональные числа (числа вида) и более общие кубические иррациональные числа. Он дал определение рациональным и иррациональным величинам, которые он и называл иррациональными числами. Он легко оперировал этими объектами, но рассуждал как об обособленных объектах, например:
 | Рациональной [величиной] является, например, 10, 12, 3%, 6% и так далее, поскольку эти величины произнесены и выражены количественно. Что не рационально, то иррационально, и невозможно произнести или представить соответствующую величину количественно. Например, квадратные корни чисел таких так 10, 15, 20 — не являющихся квадратами. |  |
В противовес концепции Евклида, что величины суть в первую очередь отрезки прямых, Аль Махани считал целые числа и дроби рациональными величинами, а квадратные и кубические корни — иррациональными. Он также ввел арифметический подход к множеству иррациональных чисел, поскольку именно он показал иррациональность следующих величин:
| результат сложения иррациональной величины и рациональной, результат вычитания рациональной величины из иррациональной, результат вычитания иррациональной величины из рациональной. | |
Египетский математик Абу Камил (ок. 850 г. н. э. — ок. 930 г. н. э.) был первым, кто счел приемлемым признать иррациональные числа решением квадратных уравнений или коэффициентами в уравнениях — в основном, в виде квадратных или кубических корней, а также корней четвёртой степени. В X веке иракский математик Аль Хашими вывел общие доказательства (а не наглядные геометрические демонстрации) иррациональности произведения, частного и результатов иных математических преобразований над иррациональными и рациональными числами. Ал Хазин (900 г. н. э. — 971 г. н. э.) приводит следующее определение рациональной и иррациональной величины:
| Пусть единична величина содержится в данной величине один или несколько раз, тогда эта [данная] величина соответствует целому числу… Каждая величина, которая составляет половину, или треть, или четверть единичной величины, или, сравненная с единичной величиной составляет три пятых от нее, это рациональная величина. И в целом, всякая величина, которая относится к единичной как одно число к другому, является рациональной. Если же величина не может быть представлена как несколько или часть (l/n), или несколько частей (m/n) единичной длины, она иррациональная, то есть невыразимая иначе как с помощью корней. | |
Многие из этих идей были позже переняты европейскими математиками после перевода на латынь арабских текстов в XII веке. Аль Хассар, арабский математик из Магриба, специализировавшийся на исламских законах о наследстве, в XII веке ввел современную символьную математическую нотацию для дробей, разделив числитель и знаменатель горизонтальной чертой. Та же нотация появилась затем в работах Фибоначчи в XIII веке. В течение XIV—XVI вв. Мадхава из Сангамаграмы и представители Керальской школы астрономии и математики исследовали бесконечные ряды, сходящиеся к некоторым иррациональным числам, например, к π, а также показали иррациональность некоторых тригонометрических функций. Джестадева привел эти результаты в книге Йуктибхаза.
Наше время
В XVII веке в математике прочно укрепились комплексные числа, вклад в изучение которых внесли Абрахам де Муавр (1667—1754) и Леонард Эйлер (1707—1783). Когда теория комплексных чисел в XIX веке стала замкнутой и чёткой, стало возможным классифицировать иррациональные числа на алгебраические и трансцендентные (доказав при этом существование трансцендентных чисел), тем самым переосмыслив работы Евклида по классификации иррациональных чисел. По этой теме в 1872 были опубликованы работы Вейерштрасса, Гейне, Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ начал рассмотрения, схожие с Гейне, именно 1872 год принято считать годом рождения теории. Вейерштрасс, Кантор и Гейне обосновывали свои теории при помощи бесконечных рядов, в то время как Дедекинд работал с (ныне так называемым) Дедекиндовым сечением множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.
Цепные дроби, тесно связанные с иррациональными числами (цепная дробь, представляющая данное число, бесконечна тогда и только тогда, когда число является иррациональным), были впервые исследованы Катальди в 1613 году, затем снова привлекли к себе внимание в работах Эйлера, а в начале XIX века — в работах Лагранжа. Дирихле также внёс значительный вклад в развитие теории цепных дробей.