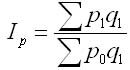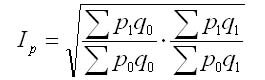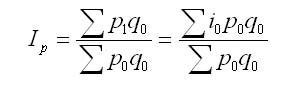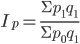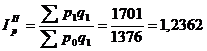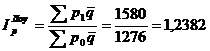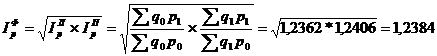Для чего используется индекс фишера
Индекс цен, индекс Пааше, индекс Ласпейреса, индекс Фишера
В условиях современной экономики и эконометрике важное место среди индексов качественных показателей отвелось индексу цен, который представляет собой показатели динамики уровня цен.
При помощи индекса потребительских цен (ИПЦ) проводится оценка динамики цен на товары производственного и непроизводственного потребления. ИПЦ отражает динамику ценконечного потребления, измеряет общее изменение стоимости фиксированного набора потребительских товаров и услуг («потребительская корзина»), а также является одним из основных показателей, характеризующих уровень инфляции. ИПЦ используется при корректировке минимального размера труда, расчета ставок налогов и т. д.
Индекс Пааше
В 1874 г. немецкий экономист Г. Пааше предложил агрегатный индекс цен с отчетными весами. Формула агрегатного индекса цен Пааше определяется так:
Где числитель — фактическая стоимость продукции отчетного периода;
Знаменатель — условная стоимость товаров, которые реализованы в отчетном периоде по базисным ценам.
Индекс цен Пааше показывает, во сколько раз возрос или уменьшился в среднем уровень цен на массу товара, реализованную в отчетном периоде, или сколько процентов составляет его рост (снижение) в отчетном периоде по сравнению с базисным периодом, т. е. он показывает, на сколько товары в отчетном периоде стали дороже (дешевле), чем в базисном.
В 1864 г. немецкий экономист Э. Ласпейрес предложил индекс, отражающий изменение цен и строится по продукции базисного периода.
Индекс Ласпейреса
Формула агрегатного индекса цен Ласпейреса рассчитывается как отношение:
Индекс цен Ласпейреса показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но по продукции, которая была реализована в базисном периоде, и экономию (перерасход), который можно было бы получить от изменения цен. Индекс цен Ласпейреса также показывает, во сколько раз товары базисного периода подорожали (подешевели) в результате изменения цен на них в отчетном периоде.
Индекс Фишера
Американский экономист И. Фишер предложил «идеальный» индекс цен, который назвали его именем, представляющий собой среднюю геометрическую произведения двух агрегатных индексов цен Ласпейреса и Пааше.
Идеальность данной формулы заключается в том, что индекс является обратимым во времени, т. е. при перестановке базисного и отчетного периодов полученный обратный индекс представляет собой величину, обратную величине первоначального индекса. Недостаток формулы состоит в том, что она лишена конкретного экономического содержания (разность между числителем и знаменателем не показывает никакой реальной экономии или потерь вследствие изменения цен).
Средний гармонический индекс цен
Средний гармонический индекс цен применяется тогда, когда неизвестны значения p1, q1 но дано их произведение и индивидуальные индексы цен ip = p1/p0 а сводный индекс должен быть исчислен с отчетными весами.
Индивидуальные индексы определены таким образом, чтобы средний гармонический индекс совпал с агрегатным.
Выражая из формулы индивидуальных индексов цен неизвестное значение р0 = p1/ip, подставляем его в знаменатель агрегатной формулы и получим средний гармонический индекс цен, который равен формуле Пааше:
Весами индивидуальных индексов iр в индексе является стоимость отдельных видов продукции отчетного периода в ценах того же периода p1q1.
Средний арифметический индекс цен
Средний арифметический индекс цен получают в том случае, если из индивидуального индекса цен ip = p1/p0 выразить цену отчетного периода p1 = i0p0, а затем подставить ее в числитель агрегатного индекса цен.
Данный индекс аналогичен агрегатному индексу Ласпейреса и имеет формулу:
В этом индексе весами осредненных индивидуальных индексов служит объем товарооборота в базисном периоде.
Индексы Ласпейреса, Пааше и Фишера. Индекс Эджворта и их экономический смысл.
В экономике в условиях рыночных отношений особое место среди индексов качественных показателей отводится индексу потребительских цен. С его помощью осуществляется оценка динамики цен и пересчет важнейших стоимостных показателей системы национальных счетов.
Рассмотрим принцип построения агрегатных индексов качественных показателей на примере индекса цен.
Если нам необходимо выявить изменения цен на различные продукты и товары или количества товаров и продуктов, то необходимо привести определенное количество товаров и продуктов по определенным ценам к общей стоимости. Для этого мы должны соизмерить «вес» каждого элемента (будь то цена или кол-во товара).
При отражении изменения цен на товары в качестве весов будет выступать количество товара. Если же необходимо отразить изменение количества товаров, то в роли «весов» будут выступать цены. Но возникает проблема: на уровне какого периода зафиксировать веса (базисного или отчетного).
Существует два способа расчета индексов цен: индексы цен Пааше и Лайспейреса.
Индекс цен Ласпейреса
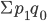

Экономическое содержание
Индекс цен Ласпейреса показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но на товары реализованные в базисном периоде. Иначе говоря индекс цен Ласпейреса показывает во сколько товары базисного периода подорожали или подешевели из-за изменения цен в отчетном периоде.
Индекс цен Пааше
Индекс цен Пааше — это агрегатный индекс цен с весами (количество реализованного товара) в отчетном периоде.


Экономическое содержание
Индекс цен Пааше характеризует изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в отчетном периоде. То есть индекс цен Пааше показывает на сколько подешевели или подорожали товары.
Значения индексов цена Пааше и Ласпейреса для одних и тех же данных не совпадают, так как имеют разное экономическое содержание и следовательно применяются в разных ситуациях.
В отечественной статистике до перехода к рыночным отношениям отдавали предпочтение индексу цен Пааше. Но из-за особенностей расчета начиная с 1991 года вычисление общего уровня цен на товары и услуги начали проводить по формуле Ласпейреса. Связано это с тем что во время инфляции или экономических кризисов многие товары могут выпасть из потребления. При исчислении по формуле Пааше не учитываются товары спрос на которые упал, поэтому при исчислении индекса цен по формуле Пааше небходим частый перерасчет информации для формировании правильной системы весов. В связи с этим и в международной практике прибегли к расчету индексов цен по формуле Ласпейреса.
Идеальный индекс цен Фишера
Представляет собой среднюю геометрическую из произведений двух агрегатных индексов цен Ласпейреса и Пааше:
Идеальность заключается в том, что индекс является обратимым во времени, то есть при перестановке базисного и отчетного периодов получается обратный индекс (величина обратная величине первоначального индекса).
Индекс цен Фишера лишен какого-либо экономического содержания. В силу сложности расчета и трудности экономической интерпретации ипользуется довольно редко (например при исчислении индексов цен за длительный период времени для сглаживания значительных изменений).
Эти формулы дают совершенно различное представление о соотношении уровней явления и естественно имеют разные результаты. В теории и практике статистики для решения этой проблемы применяется метод стандартных весов, который заключается в том, что значения индексируемой величины взвешиваются не по весам какого-либо одного региона, а по весам двух регионов вместе либо области, в которой эти регионы находятся. Для этого стоят индекс цен со стандартными весами Эджворта:

30. Индексы фиксированного и переменного состава. Индекс структурных сдвигов. Взаимосвязь индексов и их экономическое содержание.
Будучи сводной характеристикой качественного показателя, средняя величина складывается как под влиянием значений показателя у индивидуальных элементов (единиц), из которых состоит объект, так и под влиянием соотношения их весов («структуры» объекта).
индекс переменного состава; •
индекс фиксированного состава; •
индекс структурных сдвигов.
Индекс переменного состава отражает динамику среднего показателя (для однородной совокупности) за счет изменения индексируемой величины х у отдельных элементов (частей целого) и за счет изменения весов/, по которым взвешиваются отдельные значения х. Любой индекс переменного состава — это отношение двух средних величин для однородной совокупности (за два периода или по двум территориям):
Свое название этот индекс получил потому, что он характеризует динамику средних величин не только за счет изменения индексируемой величины у отдельных элементов (частей целого), но и за счет изменения удельного веса этих частей в общей совокупности, т.е. изменения состава совокупности.
Например, средняя себестоимость определенного вида продукции, выпускаемой на разных предприятиях, зависит как от уровня себестоимости на отдельных предприятиях, так и от количества продукции, выпускаемой этими предприятиями. Поэтому индекс себестоимости переменного состава отражает изменение средней себестоимости определенного продукта как за счет изменения себестоимости на каждом предприятии, так и за счет изменения удельного веса отдельных предприятий в общем выпуске продукции.
Индекс фиксированного состава отражает динамику среднего показателя лишь за счет изменения индексируемой величины х, при фиксировании весов на уровне, как правило, отчетного периода /у
Другими словами, индекс фиксированного состава исключает влияние изменения структуры (состава) совокупности на динамику средних величин, т.е. он характеризует динамику средних величин, рассчитанных для двух периодов по одной и той же фиксированной структуре весов.
По аналогии можно показать динамику среднего показателя лишь за счет изменения весов / при фиксировании индексируемой величины на уровне базисного периода х0. Такой индекс условно назван индексом структурных сдвигов (/стр):
Если от абсолютных весов перейти к относительным весам /.
пс XV’ ф-с XV,’ стр XV’
Все три формулы отражают динамику среднего показателя определенной индексируемой величины х, но в каждой из них видно, влияние какого фактора учитывается при динамике среднего показателя.
Нетрудно заметить, что индекс переменного состава есть произведение индекса фиксированного состава на индекс структурных сдвигов. Таким образом, индекс структурных сдвигов можно рассчитать путем деления индекса переменного состава на индекс фиксированного состава:
Как отмечалось в параграфе 9.1, для обозначения различных показателей в индексном методе используется определенная символика. Пользуясь ею (вместо х и /), можно записать формулы индексов переменного и фиксированного составов, а также индекса структурных сдвигов для конкретных индексируемых показателей.
Связь индексов переменного, постоянного состава и структурных сдвигов
Индекс переменного состава, зависящий от двух факторов, равен произведению индексов, на каждый из которых влияет один фактор:
Связь индексов используется для проверки расчетов и исчисления любого третьего индекса по известным двум: 0,854 « 0,857-0,996.
Проверку расчетов можно выполнить также, используя связь исчисленных приростов средних значений индексируемого показателя: прирост средней себестоимости за счет двух факторов равен сумме приростов за счет каждого фактора: 0,7 руб.
Область применения индексов переменного, постоянного состава и структурных сдвигов
В статистике товарных рынков эти индексы используются для определения влияния структуры продаж определенного товара на различных рынках на изменение средней цены товара.
62,5%. В городе А уровень цены выше, чем в городе Б, следовательно, в структуре продаж произошли отрицательные изменения.
В отчетном периоде по сравнению с базисным средняя цена картофеля в городах А и Б возросла на 28,3%, или на 1,16 руб., вследствие:
1) повышения цены в каждом городе;
2) отрицательных изменений в структуре продаж, т.е. возрастания доли продаж городом А, где уровень цены выше и в отчетном, и в базисном периодах
индекс фишера
Определение индекса цен Fisher
Формула индекса Фишера
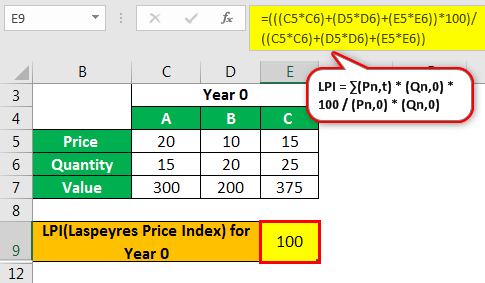
LPI = индекс цен Ласпейреса = ∑ (Pn, t) * (Qn, 0) * 100 / (Pn, 0) * (Qn, 0)
Примеры индекса цен Фишера
Сначала мы рассчитаем индекс цен Фишера для года 0, используя индекс цен Ласпейреса и индекс цен Пааше.
Индекс цен Ласпейреса за год 0 —
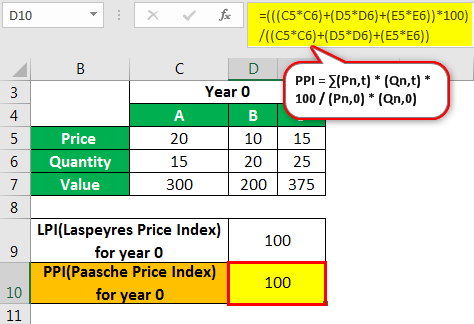
Индекс цен Пааше —
Индекс цен Fisher за год 0 —
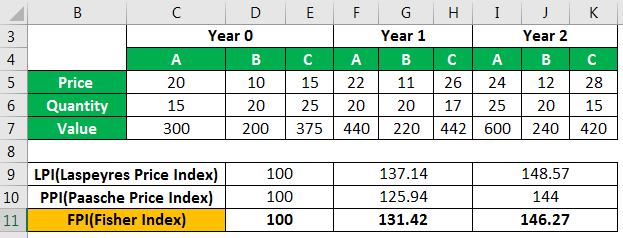
Точно так же мы находим индексы для года 1 и 2 как дано.
За 1 год
Индекс цен Ласпейреса
Индекс цен Пааше
Индекс Фишера (FPI)
На 2 год
Индекс цен Ласпейреса
Индекс цен Пааше
Индекс Фишера
Мы дали табличное представление индексов в следующей таблице.
Пример № 2
Давайте возьмем случай с тремя наиболее часто используемыми видами топлива: бензин, дизельное топливо и керосин и рассчитаем индексы цен за три года.
Цена в долларах и количество в литрах указаны в следующей таблице.
Мы можем видеть, что цены на топливо увеличились в 1-й год и снизились в 2-й. Вы заметили, что объемы также показывают аналогичную тенденцию, что неудивительно, поскольку мы знаем, что нефтегазовые компании часто сокращают добычу, когда цена сырая нефть (сырье) падает?
Таблица, показывающая значения индексов, в этом случае приведена ниже и может быть получена точно так же, как показано в приведенном выше примере.
Преимущества FPI
Недостатки ФПИ
Вывод
Хотя индекс Фишера является лучшим из трех индексов, индекс цен Ласпейреса чаще используется для расчетов инфляции. Но если мы сможем сделать точный прогноз будущих количеств товара, индекс цен Фишера дает более точную оценку.
admin
RESSA GLOBAL LTD 2018/
Индексы цен Ласпейреса, Пааше, Фишера, Лоу



Индексы цен, рассчитанные по формуле Ласпейреса, особенно широко применяются при расчете индексов потребительских цен (ИПЦ), индексов цен производителей на промышленную продукцию по данным о ценах на товары-представители. Однако данный индекс не включает инвестиционные товары, но при этом учитываются цены на импортную продукцию.
Индексы цен, рассчитанные по формуле Пааше, как правило, охватывают более широкий круг товаров и услуг. В качестве весов используется не структура потребительских расходов, а структура товарооборота, или добавленной стоимости, или произведенной продукции в текущем периоде, поэтому они могут быть определены лишь по истечении отчетного периода. Индекс цен Пааше —это индекс розничных цен, используется при измерении динамики цен компонентов ВВП, закупочных цен в сельском хозяйстве, сметных цен в строительстве, экспортных цен.
Индекс цен Ласпейреса в качестве весов использует физический объем продукции базисного периода:
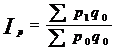
Этот индекс показывает, во сколько бы раз товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетном периоде при неизменной базисной структуре товаров-представителей, вошедших в потребительскую корзину.
Известно, что в индексе цен Ласпейреса весами служит продукция (потребительская корзина) в базисном периоде, и по мере отдаления от базисного года эта потребительская корзина все более, по видам, количеству и качеству вошедших в нее товаров-представителей, претерпевает изменение. Естественно, система весов должна пересматриваться при выборе базисного года, поэтому следует соблюсти критерии:
— базисный год должен находиться в середине длительной фазы подъема (снижения) экономического развития;
— динамика цен в базисном году не должна быть стабильной, но не должна быть и ниже, чем в соседние с ним годы;
— год должен быть «нормальным» с точки зрения различных катаклизмов.
Увязка индекса, рассчитанного по новым весам, осуществляется с помощью процедуры смыкания динамических рядов.
Индексируемой величиной виндексе цен Пааше являются цены, а весами выступает количество продукции отчетного периода.
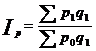
Этот индекс отвечает на вопрос: насколько товары и услуги в отчетном периоде стали дороже (дешевле), чем в базисном периоде?
Значения индексов не совпадают. Отличие значений объясняется тем, что индексы имеют разное экономическое содержание.
Индекс цен Фишера — это корень квадратный из произведения индексов цен Ласпейреса и Пааше. Экономического содержания этот индекс не имеет. Чаще всего он применяется при исчислении индексов цен за длительный период времени для сглаживания тенденций в структуре и составе объема продукции, в которых происходят значительные изменения:
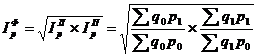
Индекс цен Фишера оценивает не только набор товаров базисного периода по ценам отчетного периода (Σq0р1), но и набор товаров отчетного периода по ценам базисного (Σq1р0). Этот индекс еще называют «идеальным» индексом, так как он является обратимым во времени.
При синтезировании общего индекса цен фактического количества товаров (в отчетный или базисный периоды) в качестве соизмерителей индексируемых величин (р1 и р0) могут применяться средние величины реализации товаров за два или большее периодов. При таком расчете формула общего индекса цен будет выглядеть следующим образом:
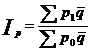
Такой индекс называется индекс Лоу. Если при определении индекса цен исходная информация содержит лишь данные о количестве реализации товаров в базисном и текущем периодах, то средняя их величина определяется: 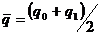
Индекс цен Лоу применяется при расчетах закупок или реализации товара в течении продолжительных периодов времени (пятилетках, десятилетиях и т.д.). Этот метод дает возможность анализа цен с учетом происходящих внутри отдельных субпериодов изменений в ассортиментном составе товаров.
Пример 1:
На основе имеющихся данных оценить изменение цен.
| товар | р0 | q0 | p1 | q1 | p0q0 | p1q1 | p0q1 | p1q0 | q cp | p0q cp | p1q cp |
| а | 15 | 10 | 17 | 15 | 150 | 255 | 225 | 170 | 12,5 | 187,5 | 212,5 |
| б | 10 | 13 | 13 | 18 | 130 | 234 | 180 | 169 | 15,5 | 155 | 201,5 |
| в | 17 | 28 | 20 | 31 | 476 | 620 | 527 | 560 | 29,5 | 501,5 | 590 |
| г | 12 | 35 | 16 | 37 | 420 | 592 | 444 | 560 | 36 | 432 | 576 |
| итого |
Задачи для самостоятельного решения:
Задача 53.
Имеются следующие данные о поставках продукта А:
| Страна-импортер | Объем поставок (тыс. шт.) | Внешнеторговая цена (долл.) | |
| базисный период, | отчетный период, | базисный период, | отчетный период, |
| Болгария | |||
| Германия | |||
| Китай | |||
| Итого | — | — |
Рассчитайте: 1) среднюю цену поставок продуктаА; 2) индексы переменного состава, постоянного состава и структурных сдвигов, характеризующие динамику средней внешнеторговой цены.
Задача 54.
Имеются данные об объемах платных услуг образования и здравоохранения:
| Услуги | Объем платных услуг в текущих ценах, ден. ед. | Изменение цен, % |
| базисный период | отчетный период | |
| 1. Образование | +10 | |
| 2. Здравоохранение в том числе: а) хирургические | +14 | |
| б)терапевтические | +17 | |
| в)другие | +10 |
Сводный индекс цен по полному набору товаров-представителей, исчисленный по формуле цен Ласпейреса, — 0,98. Определите:
1. а) как изменились бы потребительские расходы населения на приобретение платных услуг образования и здравоохранения при неизменной структуре их потребления;
б) какие факторы оказали влияние на это изменение и в какой степени;
в) как изменилась стоимость жизни.
2. Постройте сводный индекс розничных цен на платные услуги образования и здравоохранения.
3. Сделайте выводы по каждому исчисленному показателю.
Задача 55.
Рассчитайте общее и среднее изменение цен на готовую продукцию легкой промышленности, исходя из следующих данных за 8 месяцев текущего года (в % к предыдущему месяцу):
| январь | февраль | март | апрель | май | июнь | июль | Август |
| 103,3 | 102,8 | 94,6 | 99,9 | 94,5 | 101,6 | 100,9 | 106,7 |
Задача 56.
Определите индекс товарооборота; индексы цен Ласпейреса и Пааше, если известно, что за отчетный период цена единицы изделия А выросла на 5%, изделия Б – снизилась на 5%, изделия В – выросла на 11%. Объем товарооборота в отчетном периоде по изделиям А,Б,В соответственно 780, 500, 420 ден.ед., что от товарооборота базисного периода соответственно по товарам А,Б,В составляет 1,06, 0,98, 1,17.
Задача 57.
Имеются следующие данные о реализации товаров:
| Товар | Цены, ден.ед. | Объемы реализации, тыс.шт. |
| А | 5,2 | 25,1 |
| Б | 6,3 | 37,6 |
| В | 4,7 | 23,4 |
| Г | 8,5 | 40,2 |
Рассчитать индексы цен Ласпейреса, Пааше, Лоу. Сделайте выводы.
Задача 58.
Рассчитайте сводные индексы потребительских и розничных цен, исходя из данных по основным товарным группам:
| Товарные группы | Индекс цен за VI 2009 г. к XII 2008 г. | Удельный вес каждой товарной группы по состоянию на: | |
| XII 2008 г. | VI 2009 г. | ||
| Мясо и мясопродукты | 1,58 | 0,3717 | 0,2875 |
| Молоко и молочные продукты | 1,99 | 0,3109 | 0,2769 |
| Рыба и рыбопродукты | 1,89 | 0,0650 | 0,0646 |
| Сахар | 1,08 | 0,1631 | 0,1106 |
| Хлебные продукты | 2,34 | 0,0893 | 0,2604 |
| итого | 1,0000 | 1,0000 |
Задача 59.
По нижеследующим данным рассчитайте индексы цен Ласпейреса, Пааше, Фишера. Проанализируйте полученные результаты.
| Базисный период | Отчетный период | ||
| Цена за единицу, ден.ед. | Произведено, шт. | Цена за единицу, ден.ед. | Произведено, шт. |
| А | |||
| Б | |||
| В |
Задача 60.
Производство изделий в натуральном выражении снизилось в 1,2 раза по сравнению с прошлым годом, а стоимость продукции увеличилась в 2 раза. На сколько процентов выросли цены на данные изделия?
Вопросы для подготовки к экзамену по дисциплине «Экономическая статистика»
1. Предмет, методы и задачи экономической статистики
2. Система показателей экономической статистики
3. Общее понятие о классификациях, группировках и номенклатурах
4. Отраслевые классификации
5. Население как объект статистического изучения
6. Изучение численности населения
7. Движения населения. Перспективные расчеты численности населения.
8. Статистика занятости и безработицы
9. Показатели движения рабочей силы
10. Рабочее время. Баланс рабочего времени.
11. Использование рабочего времени.
12. Статистика оплаты труда. Состав фонда заработной платы.
13. Показатели уровня и динамики заработной платы. Дифференциация заработной платы
14. СНС (общие понятия).
15. Основные счета СНС
16. Система макроэкономических показателей. ВВ, ВДС.
17. Методы определения ВВП. Дефлятор ВВП.
18. Исчисление показателей ВВП в постоянных ценах
19. Национальное богатство. Классификация его элементов. Оценка национального богатства страны.
20. Виды оценки и износ основных фондов.
21. Баланс основных фондов. Показатели состояния, движения и использование основных фондов.
22. Структура финансового рынка. Кредитный рынок (общие понятия, размер кредитных вложений, средняя процентная ставка, ее динамика).
23. Кредитный рынок (валовой доход за пользование кредитами, возвратность кредита, кредитоотдача).
24. Финансы предприятия.
27. Статистическое изучение инвестиций.
28. Задачи статистики цен. Динамика средних цен.
29. Индексы цен Ласпейреса, Пааше, Фишера, Лоу. Использование индексов цен.
30. Показатели статистики уровня жизни населения.