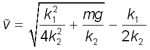Для чего используется информационное моделирование

Информационная модель объекта: что такое, какие виды существуют

Содержание:

Что такое информационная модель объекта? Это модель, которая описывает объект, применяя индивидуальную информацию, состоящую из различных взаимосвязанных параметров и переменных. Информационные модели — это неосязаемые и невидимые процессы, потому что состоят из «чистой» информации. Информация в модели, описывая объект, затрагивает:

В широком смысле, информационная модель объекта представляет собой совокупность информации из разных сфер, но объединенной описанием объекта. Пример информационной модели из жизни — это:

Что такое информационная модель объекта

Простой пример из жизни. Есть дворник, снег и снегоуборочная лопата. Словесное описание лопаты, а также инструкция по ее сборке и применению — это информационная модель лопаты для дворника. Однако это не полноценная информационная модель снегоуборочной лопаты. Еще есть задокументированное описание технологического процесса изготовления лопаты для компании производителя, сюда входят чертежи, описание изготовления, нормы по изготовлению, описание материалов для изготовления и др. Получается, что для производителя лопаты информационная модель будет своя, а для дворника своя, при этом лопата одна и та же.

Это говорит о том, что информационная модель одного и того же объекта может сильно отличаться в зависимости от того, для кого она необходима, то есть зависит от переменных.

Что такое информационная модель объекта: классификация и виды

Информационные модели могут принадлежать трем видам:

Информационные модели могут быт созданы разными способами. Отталкиваясь от способов создания, различают 2 типа моделей:

Как создаются информационные модели?

После сбора и анализа информации происходит ее «упаковка» способа подачи. Тому же дворнику, если описать процесс эксплуатации математическими формулами, будет непонятно, поэтому информационная модель лопаты для него преподносится текстом. А если прорабу описать словами каким должно быть здание, то он тоже вряд ли построит что-то путное. Поэтому информационная модель здания для прораба преподносится в виде чертежа.

Где применяются информационные модели

Любая информация вокруг вас, которая что-то описывает, объясняет или подсказывает — это информационная модель объектов.

Источник

Информационное моделирование

Цифровизация ворвалась во все сферы жизнедеятельности человека. Не осталось в стороне и строительство. Чертежный ватман и логарифмическая линейка уступили место калькулятору и графическим редакторам типа AutoCad. Нельзя говорить, что строительные проекты, уходящих эпох были хуже и примитивнее. Все дело в том, что современные методы и масштабы строительства требуют скорости, точности, четкости в планировании и взаимодействии всех звеньев. Обеспечить слаженность в работе призвана технология BIM.

BIM-технология позволяет создавать модели строительных объектов любой сложности: домов, мостов, дорог, тоннелей, скоростных автотрасс и прочего. BIM по парметрам визуализации сходно с 3D моделированием. Отличие заключается в том, что к BIM привязана обширная база данных.

Суть технологии информационного моделирования

При проектировании объекта, используя технологию BIM, в процесс одновременно могут быть включены все участвующие стороны. Техническая сторона технологии заключается в том, что 3D- объект создается из компонентов, находящихся в информационной базе. В электронную базу загружены данные о стоимости материалов, физико-механические характеристики, условия строительства: геологические, экологичесике и климатические данные. При изменении какого-либо составляющего в схеме проектируемого объекта, алгоритм мгновенно просчитает новые параметры.

Для чего необходим BIM

Возможности BIM

Building information Modeling вмещает в себя различные научные дисциплины. При помощи данной технологии в одном проекте можно объединить результаты решений по архитектуре, экономике, экологии, дизайну, инженерии.

Информационное моделирование позволяет коллективную работу над проектом. Одновременно может быть предоставлен доступ архитекторам, проектировщикам, сметчикам, дизайнерам. Каждый специалист может работать независимо от другого на своем уровне. Руководитель проекта предоставляет уровни доступа специалистам. При внесении изменений система гибко реагирует и корректирует проект одновременно на всех этапах.

Заказчикам и застройщикам BIM помогает в том, что:

Все это осуществимо только при условии создания единой информационной среды, которая обеспечит моментальный доступ к базе данных всех специалистов проекта. Возможности современных электронных систем позволяют создать виртуальную реальность, в которой возможно отслеживать и прогнозировать поведение каждого строительного узла из любой геоточки планеты.

BIM-технология в мире

Изобретение информационного моделирования повлияло на коммуникацию между специалистами в строительной индустрии, а особенно в международных проектах. Благодаря полной и достоверной информации об объекте: проектная стоимость, технологии, материалы, особенности эксплуатации- достигается эффективное взаимодействие и обмен опытом.

Великобритания

Страна, которая первая внедрила и активно развивает технолгии информационного моделирования в стрительстве. С 2016 года законодательно закреплено, что все бюджетные проекты должны создаваться при помощи BIM. Это позволяет государству отслеживать целевое расходование средств.

Соединенные Штаты Америки

Является активным пользователем BIM-технологий. В США более 70% проектных организаций применяют информационное моделирование.

Испания

С 2018 года BIM является обязательным при строителстве государственных объектов.

Китай

Страна с самой быстроразвивающейся экономикой пока не ввела обязательных требований к использованию BIM, но применение цифровых технологий в строительстве приветствуется. Китайцы оцифровали проекты по строительству атомных электростанций, что говорит о твердом решении внедрять повсеместно информационное моделирование.

Россия

Еще в 2016 году Министерство строительства России вносило инициативу об обязательном использовании BIM в стройках с государственным участием. В 2019 году понятие об информационной модели объекта капитального строительства было закреплено в Градостроительном кодексе, в статье 57. В марте 2020 Михаил Мишустин подписал постановление, согласно которому все бюджетные объекты должны создаваться при помощи BIM.

Как создается BIM-модель

Информационные технологии моделирования относительно новое направление в строительстве. Многие специалисты убеждены, что для достижения необходимого результата требуется длительное обучение, навыки программирования и глубокий опыт работы в графических редакторах. Это далеко не так. Интерфейс программного обеспечения выстроен таким образом, чтобы быть понятным всем участникам проекта. Участки по составлению сметы, финансовых отчетов, архитектурных решений, визуализации разнесены в определенные разделы. При взаимодействии с нужными разделами специалист касается только своего направления и ему не нужно расширять дополнять багаж профессиональных знаний.

В базе данных хранятся всевозможные варианты конструктивных элементов. Проектирование ведется поэтапно от подготовки основания до наивысшей степени готовности объекта к эксплуатации. По «кирпичикам» собираются и выстраиваются все элементы. Например, в упрощенном варианте работа по проекту выглядит так: согласно данным геологических изысканий, предельным состояниям грунтов и расчетных нагрузок на объекте применим ленточный фундамент. В библиотеке данных проектировщику необходимо выбрать вид фундамента, тип подушки, марку бетона, марку арматуры, материал опалубки и физические размеры фундамента. Автоматически подтянуться данные о необходимом количестве материала, его стоимости, сформируется объемный план. При этом в модели будут присутствовать не только графические изображения, но и полная информация о свойствах фундамента, включая допустимые нагрузки и предельные деформации. Далее можно подобным образом переходить к стенам и перекрытиям.

Как функционирует BIM

Чтобы получить объемную информационную модель объекта капитального строительства необходимо выполнить несколько этапов:

-предотвратить аварийные ситуации.

— отслеживать износ материалов.

— оперативно вносить изменения в конструкцию объектов, зданий и сооружений

— оснастить в короткий срок новым оборудованием объект.

— наладить взаимодействие инженерных служб.

— составить график проведения регламентных работ по обслуживанию

— контролировать оплату и расходы ресурсов: электричества, водоснабжения, водоотведения, кондиционирования, теплоснабжения.

— формировать отчет об эффективности управления недвижимостью. Сюда могут быть включены показатели по аренде, продаже площадей, оплате затрат на содержание и обслуживание.

— проводить технический аудит, планировать мероприятия по развитию инфраструктуры объекта.

Эффект от использования BIM

Анализ схожих, равнозначных реализованных строительных проектов позволяет говорить о различного рода преимуществах цифрового моделирования перед традиционным подходом. Опыт строительства с применением цифровых технологий позволил выделить наиболее яркие эффекты:

Как видно из приведенных цифр внедрение цифровых технологий неизбежно. Цифровизация не оставляет никаких шансов традиционным методам. Достижение высоких показателей и поддержание уровня эффективности возможно только при государственной поддержке, грамотном нормативно-правовом регулировании, проведении политики с четко очерченными задачами.

Перспективы цифровизации

Упоминания

Приборы отопления

Отопление помещений осуществляется в результате теплообмена. В свою очередь, теплообмен в помещении между внутренней средой и теплоносителем возможен двумя путями:

Обособленно друг от друга типы теплопередачи сложно встретить. Они всегда комбинируются между собой. Но по преобладающему принципу отопительные приборы принято называть конвекторами и излучателями или радиаторами.

Классификация отопительных приборов

В отечественной практике сформировалась следующая классификация отопителей:

Радиаторы выпускают секционные, трубчатые, панельные и блочные.

Конвекторы- с предусмотренным кожухом и без кожуха.

Высота. Низкие. Имеют размер от 200 до 400мм.; средние- 400-650; высокие- от 650 до 900мм.; плинтусные- существуют размером 200мм и меньше.

Глубина или ширина. Малая до 120мм; Средняя от 120мм до 200мм; Большая- 200мм и более.

Конвекторы делают из:

Значительно реже отопительные приборы изготавливаются из органических материалов, имеющих высокую теплопроводность и коэффициент теплоотдачи.

Все конвекторы и радиаторы выпускаются со встроенной регулировкой теплового потока или без таковой.

Различия между конвектором и радиатором

Несмотря на общие задачи, конвекторы и радиаторы имеют существенные отличия.

Способ теплоотдачи принципиально разный. Рабочий конвектор разогревает воздух, который находится в непосредственной близости. Нагретые слои воздуха увеличиваются в объеме и теряют плотность, поэтому становятся легче более холодных слоев. Теплый воздух стремиться к потолку. Внизу, у конвектора образуется зона разрежения, куда засасывается холодный воздух, который снова разогревается и устремляется к потолку. И так постоянно, до выравнивания температуры конвектора и температуры в помещении в любой точке. Ускорить и усилить конвективные потоки помогает кожух, который выполняет роль вытяжного канала.

Радиаторы более термоинертны. То есть тепловому прибору требуется больше времени для разогрева, так как он обладает повышенной теплоемкостью по сравнению с конвектором. Но и остывать радиатор будет дольше. В определенных ситуациях это может быть как плюсом, так и минусом.

Конвекторы окрашивают в разные цвета. Радиаторы традиционно встречаются в белом исполнении, что может потребовать коррекции в дизайнерском интерьере. Белый цвет применим по соображениям его респектабельности и универсальности, но, по законам физики, наибольшей теплоотдачей будет обладать поверхность черного цвета.

Преимущества и недостатки отопительных приборов

Радиатор отличает в лучшую сторону надежность, долговечность, невысокая цена. Термоинерция играет в плюс, когда происходят перебои с отоплением. Но когда нужно отрегулировать температуру на комфортный уровень этот показатель доставляет неудобства.

Очевидным минусом радиаторов служит высокая температура разогрева поверхности. Она приближена к температуре теплоносителя в системе. В системе центрального теплоснабжения температура может достигать 80 0 C и более. Есть угроза получения ожогов. Избежать этого можно, установив защитный корпус или защитный экран. Но в этом случае падает мощность отопителя.

К достоинствам конвекторов можно отнести небольшую массу, возможность скрытой установки и монтажа в сложных местах, например, под панорамными окнами. Невысокую температуру поверхности конвекторных пластин, в районе 50 0 С, что не приведет к ожогам. Конвекторы быстрее и полнее прогревают помещение.

Существенным минусом конвекторов выступает то, что в результате циркуляции конвекционных потоков в окружающий воздух поднимается пыль.

Нецелесообразно применять конвекторы в помещениях с высокими потолками.

Требования безопасности к отопительным приборам

Поверхность конвекторов и радиаторов не должна иметь острых краев и быть травмобезопасной.

В случае, если технологически предусмотрено нагревание поверхности отопительного прибора до температуры превышающей 75 0 С, то должны устанавливаться защитные экраны

Для окраски приборов отопления необходимо применять порошковые, лакокрасочные материалы, которые не выделяют в процессе эксплуатации вредных и токсичных веществ.

Использование батарей централизованного отопления для организации заземления или токопроводящих работ запрещено.

Не допускается производить выпуск воздушной смеси из алюминиевого прибора в процессе эксплуатации при наличии поблизости открытого огня.

От чего зависит выбор отопительных приборов

Приборы отопления должны соответствовать конкретным проектным требованиям эксплуатации. Запрещено применять отопительные приборы, у которых показатели по температуре теплоносителя и давлению ниже, чем требуемых условий по эксплуатации сети.

Утилизацию радиаторов и конвекторов требуется осуществлять в соответствии с нормативной документацией завода- изготовителя.

Для правильного выбора приборов для отопления жилища или производственного помещения стоит опираться на ряд критериев, которые помогут сориентироваться в многообразии.

Как выбрать отопительный прибор

Удачно вписываются в указанные требования для систем централизованного отопления чугунные секционные батареи и биметаллические секционные приборы. Секционные приборы имеют возможность дооснащаться необходимым количеством элементов, что делает их универсальными.

Чугунные секционные батареи. Самые недорогие на сегодняшний день отопительные приборы. Имеют отличный запас прочности и долговечности. Радиаторы из чугуна служат до 50 лет. Продукция из чугуна стойка к гидроударам и коррозийным процессам. На рынке отопительной продукции можно встретить чугунные батареи художественного литья, тем самым можно подчеркнуть дизайнерский стиль интерьера. Однозначно не позволяет сделать выбор в пользу чугунины то, что материал тяжелый и имеет непрезентабельный вид. Если не брать во внимание художественное литье. У чугуна высокая теплоемкость, поэтому требуется время, чтобы его разогреть, но в то же время батарея долго остывает. Это минус, когда требуется оперативно отрегулировать температурный режим.

Биметаллические секционные приборы. Приборы из биметалла лишены недостатков чугуна, и имеют свои преимущества: рассчитаны на высокое давление в сети; имеют современный внешний вид. Но дороже чугуна по стоимости. Биметаллические изделия представляют собой стальной сердечник в виде труб, облитый алюминием по форме готовой батареи. Такая конструкция создавалась для того, чтобы исключить контакт алюминия с теплоносителем, так как вода в системе теплоснабжения довольно реактивна по отношению к алюминию.

Алюминиевые изделия. Отопительные батареи из алюминия обладают отличным коэффициентом теплоотдачи, имеют высокий КПД. Из недостатков можно выделить высокую стоимость и данный тип приборов не предназначен для сетей с высоким давлением теплового агента. Вдобавок алюминий не стоек к воздействию агрессивных сред. Поэтому алюминиевые тепловые приборы целесообразно использовать в частном теплоснабжении, где рабочее давление не превышает 8 атмосфер и теплоагент в составе несет минимум солей.

У секционных приборов, независимо от материала изготовления, есть общий недостаток. Они не предназначены для работы с антифризом. Со временем антифриз уменьшает уплотнительную способность межсекционной прокладки и появляется течь.

Панельные отопители. Делаются из стали. Штампуются два листа, симметричных между собой относительно продольной плоскости и свариваются. Таким образом получается плоский отопительный элемент, внутри которого есть каналы для циркуляции теплоагента. Далее отдельные элементы связываются между собой трубами в единую батарею. Полученная прямоугольная панель закрывается декоративным кожухом, но может обходиться без него. Без защитного экрана эффективность прибора выше, но страдает привлекательность. Стальные отопительные панельные приборы имеют хорошую теплоотдачу, современный вид. Можно устанавливать и в частном домостроении и интегрировать в централизованную магистраль.

Трубчатые отопительные приборы. Похожи на секционные отопители по форме. Выглядят как радиаторы из изогнутых вертикальных трубок, соединенных сверху и снизу трубчатым коллектором. Очень вариативны по размерам: от 0,3 метра до 3 метров. Устанавливаются в жилых и производственных помещениях, независимо от системы теплоснабжения.

Конвекторы. Производят из стали, меди и алюминия. Наиболее физически эффективны медные конвекторы. Изготавливаются конвекторы из центральной трубы диаметром до 3см, с нанизанными на нее пластинами. Между пластинами происходит прогрев воздуха. Конвекторы бывают настенной и скрытой установки. На настенные конвекторы одевается специальный кожух, который обеспечивает эффект тяги воздушным массам. Конвекторы скрытой установки могут монтироваться в пол и располагаться под панорамными окнами. Тепловые приборы на основе конвекции существуют естественной и принудительной циркуляции. Искусственная циркуляция достигается применением вентилятора в системе. Конвекторы имеют хороший коэффициент полезного действия, но имеют трудности в очистке от пыли.

Сколько тепловых приборов нужно в помещении

В помещении, согласно технологии установки тепловых приборов, требуется монтаж отопителя под каждым окном. Так как основная цель отопительных приборов компенсировать теплопотери, то и мощность приборов основывается на суммировании коэффициентов тепловых потерь. По усредненным теплотехническим расчетам, при высоте потолка в 2,7 м. 1м 3 жилища в панельном доме требует 40Вт тепловой энергии, а кирпичный 35 Вт. Исходя из этого можно посчитать общую мощность обогревателей. На конечный результат будут играть факторы: отношение площади остекленной поверхности к площади стен; площадь наружных стен в помещении и степень утепленности, теплопотери потолка и пола, тип стеклопакета, амплитуда колебаний температур. В частном доме учитываются коэффициенты теплопотерь крыши и фундамента. Каждому фактору присвоен коэффициент, который можно найти в таблицах по теплотехническим расчетам.

Итог тепловой системы приборов

В результате подбора приборов по личным и техническим критериям должна получится система, которая отвечает эксплуатационным пунктам:

Отопительная система должна быть надежной и безопасной, не сильно затратной, простой в обслуживании.

Управление температурным режимом продублировано: автоматика- ручное.

Последовательность действий по управлению приборами должно быть простым и логичным.

Должна быть исключена вероятность нанесения ущерба системе по незнанию пользователя.

В частном жилье меры по предотвращению разморозки отопительной системы обязательны.

Отопительная система должна быть собрана из качественных материалов, согласно теплотехническому расчету, законов физики и здравого смысла.

Источник

IV. Информационное моделирование

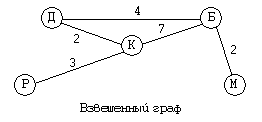
Список статей

1. Графические модели

2. Имитационные модели

3. Математические модели

4. Моделирование процессов оптимального планирования

5. Моделирование глобальных процессов

6. Моделирование физических систем и процессов

7. Моделирование экологических систем и процессов

8. Объектно-информационные модели

9. Системный анализ

10. Статистические модели

11. Табличные модели

12. Формализация и моделирование

В школьном курсе информатики традиционно присутствует содержательная линия формализации и моделирования. Понятие модели относится к фундаментальным общенаучным понятиям, а моделирование — это метод познания действительности, используемый различными науками.

Практически во всех естественных и социальных науках построение и использование моделей является мощным орудием исследований. Реальные объекты и процессы бывают столь многогранны и сложны, что лучшим способом их изучения оказывается построение модели, отображающей лишь какую-то часть реальности и потому многократно более простой, чем эта реальность. Предметом исследования и разработки информатики является методология информационного моделирования, связанная с использованием компьютерной техники и технологий. В этом смысле говорят о компьютерном моделировании. Межпредметное значение информатики в значительной степени проявляется именно через внедрение компьютерного моделирования в различные научные и прикладные области: физику и технику, биологию и медицину, экономику, управление и многие другие.

Компьютерное моделирование включает в себя процесс реализации информационной модели на компьютере и исследование с помощью этой модели объекта моделирования — проведение вычислительного эксперимента. С помощью компьютерного моделирования решаются многие научные и производственные задачи.

Информационное моделирование связано с формализацией данных об объекте моделирования (см. “Формализация и моделирование”). Построение информационной модели начинается с определения целей моделирования и анализа объекта моделирования как сложной системы, в которой требуется выделить отражаемые в модели свойства и отношения между ними (см. “Системный анализ”). Информационные модели различаются по форме представления информации об объекте моделирования. Математические модели используют язык математики для представления объекта моделирования. Отдельной разновидностью математических моделей являются статистические модели — ориентированные на обработку массовых данных (например, опросов населения), в которых имеется элемент случайности. Данные об объекте моделирования, организованные в табличной форме, составляют табличную модель. Графические средства используются для построения графических моделей. Возникший в конце прошлого столетия объектно-ориентированный подход к программированию породил новую парадигму в информационном моделировании: объектно-информационное моделирование. Компьютерные модели, воспроизводящие поведение сложных систем, для описания которых нет однозначного математического аппарата, называются имитационными моделями.

Компьютерное информационное моделирование используется для описания и анализа процессов разнообразной природы. Наибольший опыт в этом отношении имеют физические науки (см. “Моделирование физических систем и процессов”). Компьютерное моделирование помогает решать важные проблемы экологии (см. “Моделирование экологических систем и процессов”). Большую роль играет информационное моделирование в экономике и управлении. Важнейшими задачами этой области являются задачи планирования (см. “Моделирование процессов оптимального планирования”). Средствами компьютерного моделирования ученые пытаются решить даже такую глобальную проблему, как судьбы человеческой цивилизации (см. “Моделирование глобальных процессов”).

1. Графические модели

Разнообразие графических моделей достаточно велико. Рассмотрим некоторые из них.

Наглядным средством отображения состава и структуры систем (см. “Системология”) являются графы.

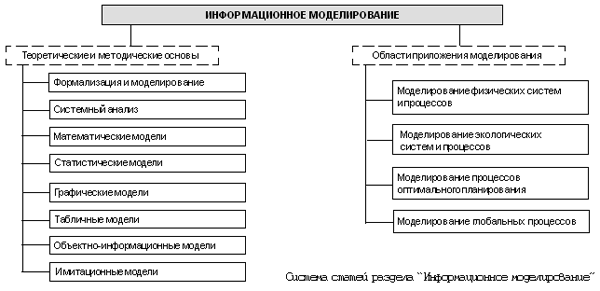
Рассмотрим пример. Имеется словесное описание некоторой местности: “Наш район состоит из пяти поселков: Дедкино, Бабкино, Репкино, Кошкино и Мышкино. Автомобильные дороги проложены между: Дедкино и Бабкино, Дедкино и Кошкино, Бабкино и Мышкино, Бабкино и Кошкино, Кошкино и Репкино”. По такому описанию довольно трудно представить себе эту местность. Гораздо легче та же информация воспринимается с помощью схемы (см. рисунок). Это не карта местности. Здесь не выдержаны направления по сторонам света, не соблюден масштаб. На этой схеме отражен лишь факт существования пяти поселков и дорожной связи между ними. Такая схема, отображающая элементный состав системы и структуру связей, называется графом.

Составными частями графа являются вершины и ребра. На рисунке вершины изображены кружками — это элементы системы, а ребра изображены линиями — это связи (отношения) между элементами. Глядя на этот граф, легко понять структуру дорожной системы в данной местности.

Построенный граф позволяет, например, ответить на вопрос: через какие поселки надо проехать, чтобы добраться из Репкино в Мышкино? Видно, что есть два возможных пути: 1) Р К Б М и) Р К Д Б М. Можно ли отсюда сделать вывод, что 1-й путь короче 2-го? Нет, нельзя. Данный граф не содержит количественных характеристик. Это не карта, где соблюдается масштаб и есть возможность измерить расстояние.

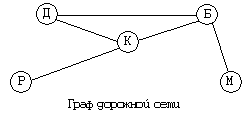
Граф, приведенный на следующем рисунке, содержит количественные характеристики. Числа около ребер обозначают длины дорог в километрах. Это пример взвешенного графа. Взвешенный граф может содержать количественные характеристики не только связей, но и вершин. Например, в вершинах может быть указано население каждого поселка. Согласно данным взвешенного графа, оказывается, что первый путь длиннее второго.

Подобные графы еще называют сетью. Для сети характерна возможность множества различных путей перемещения по ребрам между некоторыми парами вершин. Для сетей также характерно наличие замкнутых путей, которые называются циклами. В данном случае имеется цикл: К Д Б К.

На рассмотренных схемах каждое ребро обозначает наличие дорожной связи между двумя пунктами. Но дорожная связь действует одинаково в обе стороны: если по дороге можно проехать от Б к М, то по ней же можно проехать и от М к Б (предполагаем, что действует двустороннее движение). Такие графы являются неориентированными, а их связи называют симметричными.

Качественно иной пример графа изображен на следующем рисунке.

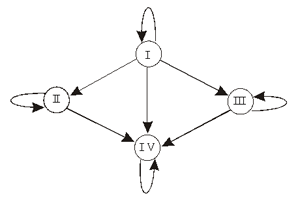
Граф совместимости групп крови

Этот пример относится к медицине. Известно, что у разных людей кровь отличается по группе. Существуют четыре группы крови. Оказывается, что при переливании крови от одного человека к другому не все группы совместимы. Граф показывает возможные варианты переливания крови. Группы крови — это вершины графа с соответствующими номерами, а стрелки указывают на возможность переливания одной группы крови человеку с другой группой крови. Например, из этого графа видно, что кровь I группы можно переливать любому человеку, а человек с I группой крови воспринимает только кровь своей группы. Видно также, что человеку с IV группой крови можно переливать любую, но его собственную кровь можно переливать только в ту же группу.

Связи между вершинами данного графа несимметричны и поэтому изображаются направленными линиями со стрелками. Такие линии принято называть дугами (в отличие от ребер неориентированных графов). Граф с такими свойствами называется ориентированным. Линия, выходящая и входящая в одну и ту же вершину, называется петлей. В данном примере присутствуют четыре петли.

Нетрудно понять преимущества изображения модели системы переливания крови в виде графа по сравнению со словесным описанием тех же самых правил. Граф легко воспринимается и запоминается.

Весьма распространенным типом систем являются системы с иерархической структурой. Иерархическая структура естественным образом возникает, когда объекты или некоторые их свойства находятся в отношении соподчинения (вложения, наследования). Как правило, иерархическую структуру имеют системы административного управления, между элементами которых установлены отношения подчиненности. Например: директор завода — начальники цехов — начальники участков — бригадиры — рабочие. Иерархическую структуру имеют также системы, между элементами которых существуют отношения вхождения одних в другие.

Граф иерархической структуры называется деревом. Основным свойством дерева является то, что между любыми двумя его вершинами существует единственный путь. Деревья не содержат циклов и петель.

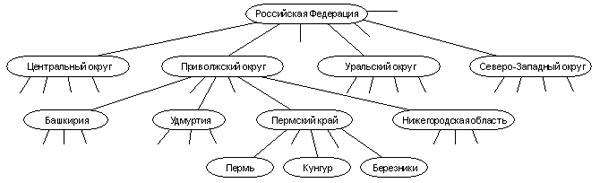
Посмотрите на граф, отражающий иерархическую административную структуру нашего государства: Российская Федерация делится на семь административных округов; округа делятся на регионы (области и национальные республики), в состав которых входят города и другие населенные пункты. Такой граф называется деревом.

Дерево административной структуры РФ

У дерева существует одна главная вершина, которая называется корнем дерева. Эта вершина изображается вверху; от нее идут ветви дерева. От корня начинается отсчет уровней дерева. Вершины, непосредственно связанные с корнем, образуют первый уровень. От них идут связи к вершинам второго уровня и т.д. Каждая вершина дерева (кроме корня) имеет одну исходную вершину на предыдущем уровне и может иметь множество порожденных вершин на следующем уровне. Такой принцип связи называется “один ко многим”. Вершины, которые не имеют порожденных, называются листьями (на нашем графе это вершины, обозначающие города).

Общую цель научной графики можно сформулировать так: сделать невидимое и абстрактное “видимым”. Последнее слово заключено в кавычки, так как эта “видимость” часто весьма условна. Можно ли увидеть распределение температуры внутри неоднородно нагретого тела сложной формы без введения в него сотен микродатчиков, т.е., по существу, его разрушения? — Да, можно, если есть соответствующая математическая модель и, что очень важно, договоренность о восприятии определенных условностей на рисунке. Можно ли увидеть распределение металлических руд под землей без раскопок? Строение поверхности чужой планеты по результатам радиолокации? На эти и множество других вопросов ответ — да, можно, с помощью компьютерной графики и предшествующей ей математической обработки.

Более того, можно “увидеть” и то, что, строго говоря, вообще плохо соответствует слову “видеть”. Так, возникшая на стыке химии и физики наука — квантовая химия — дает нам возможность “увидеть” строение молекулы. Эти изображения — верх абстракции и системы условностей, так как в атомном мире обычные наши понятия о частицах (ядрах, электронах и т.п.) принципиально неприменимы. Однако многоцветное “изображение” молекулы на экране компьютера для тех, кто понимает всю меру его условности, приносит большую пользу, чем тысячи чисел, являющихся результатами вычислений.

Изолинии

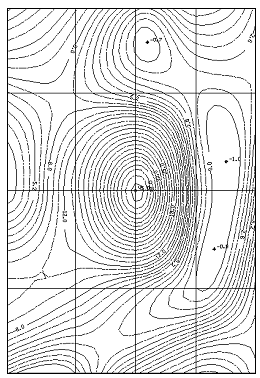
Стандартным приемом обработки результатов вычислительного эксперимента является построение линий (поверхностей), называемых изолиниями (изоповерхностями), вдоль которых некоторая функция имеет постоянное значение. Это очень распространенный прием визуализации характеристик некоторого скалярного поля в приближении сплошной среды: изотермы — линии равной температуры, изобары — линии равного давления, изолинии функции тока жидкости или газа, по которым легко можно представить себе их потоки, изолинии численностей экологической популяции на местности, изолинии концентрации вредных примесей в окружающей среде и т.д.

На рисунке изображены изолинии функции тока неравномерно нагретой жидкости в прямоугольной области течения. По этой картине можно наглядно судить о направлении потоков течения и их интенсивности.

Условные цвета, условное контрастирование

Еще один интересный прием современной научной графики — условная раскраска. Она находит широчайшее применение в самых разных приложениях науки и представляет собой набор приемов по максимально удобной визуализации результатов компьютерного моделирования.

В различных исследованиях температурных полей встает проблема наглядного представления результатов, например, температур на метеорологических картах. Для этого можно рисовать изотермы на фоне карты местности. Но можно добиться еще большей наглядности, учитывая, что большинству людей свойственно воспринимать красный цвет как “горячий”, синий — как “холодный”. Переход по спектру от красного к синему отражает промежуточные значения температур.

То же самое можно делать при иллюстрации температурного поля и на поверхности обрабатываемой на станке детали, и на поверхности далекой планеты.

При моделировании сложных органических молекул компьютер может выдавать результаты в виде многоцветной картины, на которой атомы водорода изображены одним цветом, углерода — другим и т.д., причем атом представлен шариком (кружочком), в пределах которого плотность цвета меняется в соответствии с распределением электронной плотности. При поиске полезных ископаемых методами аэрофотосъемки с самолетов или космических спутников компьютеры строят условные цветовые изображения распределений плотности под поверхностью Земли.

Изображения в условных цветах и контрастах — мощнейший прием научной графики. Он позволяет понять строение не только плоских, но и объемных (трехмерных) объектов, дает в руки исследователя один из замечательных методов познания.

Методические рекомендации

Не следует путать изучение графического информационного моделирования с изучением технологий обработки графической информации. Когда ученики приступают к изучению моделирования, то обычно они уже знакомы с базовыми технологиями компьютерной графики: умеют пользоваться простыми графическими редакторами, умеют строить диаграммы в табличном процессоре или иной подходящей программе.

Построение простых графических моделей в форме графов и иерархических структур уместно уже в базовом курсе информатики в рамках изучения темы “Формализация и моделирование”. Построение генеалогического дерева семьи, иерархической системы школьного управления и т.п. является относительно несложным занятием, доступным большинству учащихся. При этом уместно использовать иллюстративные возможности систем компьютерной графики.

Что же касается самостоятельной реализации моделей научной графики через программирование, то это — материал повышенной трудности, практическая отработка которого уместна в профильном курсе информатики или в рамках элективного курса, направленного на углубленное изучение моделирования физических и других процессов.

2. Имитация модели

Имитационная модель воспроизводит поведение сложной системы взаимодействующих элементов. Для имитационного моделирования характерно наличие следующих обстоятельств (одновременно всех или некоторых из них):

· объект моделирования — сложная неоднородная система;

· в моделируемой системе присутствуют факторы случайного поведения;

· требуется получить описание процесса, развивающегося во времени;

· принципиально невозможно получить результаты моделирования без использования компьютера.

Состояние каждого элемента моделируемой системы описывается набором параметров, которые хранятся в памяти компьютера в виде таблиц. Взаимодействия элементов системы описываются алгоритмически. Моделирование осуществляется в пошаговом режиме. На каждом шаге моделирования изменяются значения параметров системы. Программа, реализующая имитационную модель, отражает изменение состояния системы, выдавая значения ее искомых параметров в виде таблиц по шагам времени или в последовательности происходящих в системе событий. Для визуализации результатов моделирования часто используется графическое представление, в т.ч. анимированное.

Имитационная модель основана на подражании реальному процессу (имитации). Например, моделируя изменение (динамику) численности микроорганизмов в колонии, можно рассматривать много отдельных объектов и следить за судьбой каждого из них, ставя определенные условия для его выживания, размножения
и т.д. Эти условия обычно задаются в вербальной форме. Например: по истечении некоторого промежутка времени микроорганизм делится на две части, а по прошествии другого (большего) временноRго отрезка — погибает. Выполнение описанных условий алгоритмически реализуется в модели.

Другой пример: моделирование движения молекул в газе, когда каждая молекула представляется в виде шарика с определенным направлением и скоростью движения. Взаимодействие двух молекул или молекулы со стенкой сосуда происходит согласно законам абсолютно-упругого столкновения и легко описывается алгоритмически. Получение интегральных (общих, усредненных) характеристик системы производится на уровне статистической обработки результатов моделирования.

Такой компьютерный эксперимент фактически претендует на воспроизведение натурного эксперимента. На вопрос: “Зачем это нужно делать?” можно дать следующий ответ: имитационное моделирование позволяет выделить “в чистом виде” следствия гипотез, заложенных в представления о микрособытиях (т.е. на уровне элементов системы), избавив их от неизбежного в натурном эксперименте влияния других факторов, о которых мы можем даже не подозревать. Если такое моделирование включает и элементы математического описания процессов на микроуровне, и если исследователь при этом не ставит задачу поиска стратегии регулирования результатов (например, управления численностью колонии микроорганизмов), то отличие имитационной модели от математической (дескриптивной) оказывается достаточно условным.

Приведенные выше примеры имитационных моделей (эволюция колонии микроорганизмов, движение молекул в газе) приводят к детерминированному описанию систем. В них отсутствуют элементы вероятности, случайности событий в моделируемых системах. Рассмотрим пример моделирования системы, обладающей этими качествами.

Кому не случалось стоять в очереди и с нетерпением прикидывать, успеет ли он сделать покупку (или заплатить за квартиру, покататься на карусели и т.д.) за некоторое имеющееся в его распоряжении время? Или, пытаясь позвонить по телефону в справочную и натыкаясь несколько раз на короткие гудки, нервничать и оценивать — дозвонюсь или нет? Из таких “простых” проблем в начале XX века родилась новая отрасль математики — теория массового обслуживания, использующая аппарат теории вероятностей и математической статистики, дифференциальных уравнений и численных методов. Впоследствии выяснилось, что эта теория имеет многочисленные выходы в экономику, военное дело, организацию производства, биологию и экологию и т.д.

Компьютерное моделирование при решении задач массового обслуживания, реализуемое в виде метода статистических испытаний (метода Монте-Карло), играет важную роль. Возможности аналитических методов решения реально возникающих задач массового обслуживания весьма ограничены, в то время как метод статистических испытаний универсален и относительно прост.

Рассмотрим простейшую задачу этого класса. Имеется магазин с одним продавцом, в который случайным образом входят покупатели. Если продавец свободен, то он начинает обслуживать покупателя сразу, если зашло одновременно несколько покупателей — выстраивается очередь. Есть немало других аналогичных ситуаций:

· ремонтная зона в автохозяйстве и автобусы, сошедшие с линии из-за поломки;

· травмпункт и больные, пришедшие на прием по случаю травмы (т.е. без системы предварительной записи);

· телефонная станция с одним входом (или одной телефонисткой) и абоненты, которых при занятом входе ставят в очередь (такая система иногда практикуется);

· сервер локальной сети и персональные машины на рабочем месте, которые шлют сообщение серверу, способному воспринять разом и обработать не более одного сообщения.

Процесс прихода покупателей в магазин — случайный процесс. Промежутки времени между приходами любой последовательной пары покупателей — независимые случайные события, распределенные по некоторому закону, который может быть установлен лишь путем многочисленных наблюдений (либо для моделирования взят некоторый его правдоподобный вариант). Второй случайный процесс в этой задаче, никак не связанный с первым, — длительность обслуживания каждого из покупателей.

Целью моделирования систем такого вида является получение ответа на ряд вопросов. Относительно простой вопрос — какое в среднем время придется стоять в очереди при заданных законах распределения указанных выше случайных величин? Более сложный вопрос: каково распределение времен ожидания обслуживания в очереди? Не менее сложный вопрос: при каких соотношениях параметров входных распределений наступит кризис, при котором очередь до вновь вошедшего покупателя не дойдет никогда? Если задуматься над этой относительно простой задачей, возможные вопросы будут множиться.

Способ моделирования выглядит в общих чертах так. Используемые математические формулы — законы распределения исходных случайных величин; используемые числовые константы — эмпирические параметры, входящие в эти формулы. Не решается никаких уравнений, которые использовались бы при аналитическом исследовании данной задачи. Вместо этого происходит имитация очереди, разыгрываемая с помощью компьютерных программ, генерирующих случайные числа с заданными законами распределения. Затем производится статистическая обработка совокупности полученных значений величин, определяемых заданными целями моделирования. Например, находится оптимальное количество продавцов для разных периодов времени работы магазина, которое обеспечит отсутствие очередей. Математический аппарат, который здесь используется, называется методами математической статистики.

В статье “Моделирование экологических систем и процессов” 2 описан другой пример имитационного моделирования: одна из многих моделей системы “хищник—жертва”. Особи видов, находящихся в указанных отношениях, по определенным правилам, содержащим элементы случайности, перемещаются, хищники съедают жертв, и те и другие размножаются и т.д. Такая модель не содержит никаких математических формул, но требует статистической обработки результатов.

Пример алгоритма детерминированной имитационной модели

Рассмотрим имитационную модель эволюции популяции живых организмов, известную под названием “Жизнь”, которую легко реализовать на любом языке программирования.

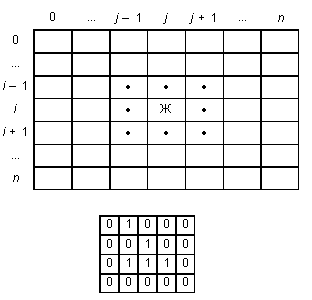
Для построения алгоритма игры рассмотрим квадратное поле из n + 1 столбцов и строк с обычной нумерацией от 0 до n. Крайние граничные столбцы и строки для удобства определим как “мертвую зону”, они играют лишь вспомогательную роль.

Для любой внутренней клетки поля с координатами (i, j) можно определить 8 соседей. Если клетка “живая”, ее закрашиваем, если клетка “мертвая”, она пустая.

Зададим правила игры. Если клетка (i, j) “живая” и ее окружает более трех “живых” клеток, она погибает (от перенаселения). “Живая” клетка также погибает, если в ее окружении находится менее двух “живых” клеток (от одиночества). “Мертвая” клетка оживает, если вокруг нее появляются три “живые” клетки.

Для удобства введем двумерный массив A[0..n, 0..n], элементы которого принимают значение 0, если соответствующая клетка пустая, и 1, если клетка “живая”. Тогда алгоритм определения состояния клетки с координатой (i, j) можно определить следующим образом:

+ А[I + 1, J] + А[I + 1, J + 1] +

(S Контуры обратных связей чсленности населения, капитала, сельскохозяйственного производства и загрязнения окружающей среды

Понятия положительной и отрицательной обратной связи взяты из теории автоматического регулирования (раздела кибернетики). Причинно-следственная связь между двумя элементами называется отрицательной, если изменение одного элемента передается второму, возвращается от него к первому и изменяет его в направлении, противоположном первоначальному (подавляет), и положительной, если это изменение, возвращаясь к первому, усиливает его. Если элементов не два, а больше, то говорят о контуре обратной связи, через которую сигнал проходит по кругу, возвращаясь к источнику и влияя на него.

Некоторый набор таких рисунков графически исчерпывает модель WORLD. Однако за каждой стрелкой — первичные взаимосвязи, а за каждой из них — уравнения, в которые входит ряд параметров. Фактически именно значения этих параметров и определяют результаты, поэтому к их анализу привлекаются как многочисленные узкие специалисты, так и многие эмпирические (статистические) данные, собранные в десятках справочников, отчетов ООН и отдельных государств. Количество взаимосвязанных переменных в модели WORLD-3 равно 225, параметров — еще больше.

Результаты глобального моделирования

Опубликованные “сценарии” развития человечества, следующие из моделей WORLD, охватывают промежуток времени от 1900 до 2100 года. Первые 100 лет, уже прошедшие, позволяют “настраивать” модель, определить степень ее достоверности.

Первый из сценариев основан на гипотезе, что все будет развиваться без серьезных изменений, глобальных политических катаклизмов, без особых усилий по сохранению ресурсов и уменьшению загрязнения окружающей среды. Модель предсказывает катастрофические результаты такого развития.

Вместе с тем модель WORLD позволяет найти пути регулируемого развития, которое ведет к плавному (“сигмоидному”) поведению основных переменных. Этот путь связан с самоограничениями и переходом на усовершенствованные промышленные и сельскохозяйственные технологии.

Постановка задачи оптимального планирования

Планирование — важнейший этап экономической и управленческой деятельности. Объектом планирования может быть деятельность подразделения или всего предприятия, отрасли промышленности или сельского хозяйства, региона, наконец, государства.

Постановка задачи планирования в общем случае выглядит следующим образом:

· имеются некоторые плановые показатели: X, Y, …;

· имеются некоторые ресурсы: R1, R2, …, за счет которых эти плановые показатели могут быть достигнуты;

· имеется определенная стратегическая цель, зависящая от значений плановых показателей, на которую следует ориентировать планирование.

Задача оптимального планирования заключается в определении значений плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели.

Приведем примеры. Пусть объектом планирования является детский сад. Ограничимся лишь двумя плановыми показателями: числом детей и числом воспитателей. Основными ресурсами деятельности детского сада являются размер финансирования и размер помещения. А каковы стратегические цели? Естественно, одной из них является сохранение и укрепление здоровья детей. Количественной мерой этой цели является минимизация заболеваемости воспитанников детского сада.

Другой пример: планирование экономической деятельности государства. Безусловно, это слишком сложная задача для детального анализа. Плановых показателей очень много: это производство различных видов промышленной и сельскохозяйственной продукции, подготовка специалистов, выработка электроэнергии, размер зарплаты работников бюджетной сферы и многое другое. К ресурсам относятся: количество работоспособного населения, бюджет государства, природные ресурсы, энергетика, возможности транспортных систем и пр. Разумеется, каждый из этих видов ресурсов ограничен. Кроме того, важнейшим ресурсом является время, отведенное на выполнение плана.

Вопрос о стратегических целях в этом случае очень сложен. У государства их много, но в разные периоды истории приоритеты могут меняться. Например, в военное время главной целью является максимальная обороноспособность, военная мощь страны. В мирное время в современном цивилизованном государстве приоритетной целью должно быть достижение максимального уровня жизни населения.

Решение задач оптимального планирования чаще всего является сложным и недоступным при использовании лишь человеческого опыта (эмпирических методов). Для решения таких задач строится математическая модель, устанавливающая связь между параметрами задачи. Следовательно, оптимальное планирование осуществляется путем применения математического моделирования. Как правило, такие модели для реальных ситуаций не поддаются аналитическому решению, поэтому используются численные методы решения, реализуемые на компьютере.

Пример математической модели оптимального планирования

Рассмотрим простой пример, с помощью которого можно получить представление об одном из классов задач оптимального планирования.

Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности емкости склада за день можно приготовить в совокупности не более 700 изделий. Рабочий день в кондитерском цехе длится 8 часов. Поскольку производство пирожных более трудоемко, то, если выпускать только их, за день можно произвести не более 250, пирожков же можно произвести 1000 (если при этом не выпускать пирожных). Стоимость пирожного вдвое выше, чем пирожка. Требуется составить дневной план производства, обеспечивающий кондитерскому цеху наибольшую выручку.

Сформулируем эту задачу математически. Плановыми показателями являются:

x — дневной план выпуска пирожков;

y — дневной план выпуска пирожных.

Ресурсы производства — это:

· длительность рабочего дня — 8 часов;

· вместимость складского помещения — 700 мест.

К двум полученным неравенствам следует добавить условия положительности значений величин x и y (не может быть отрицательного числа пирожков и пирожных). В итоге мы получили систему неравенств:

x + 4y 1000, x + y 700, x 0, y 0 ()

Формализуем стратегическую цель: получение максимальной выручки. Выручка — это стоимость всей проданной продукции. Пусть цена одного пирожка r рублей. По условию задачи, цена пирожного в два раза больше, т.е. 2r рублей. Отсюда стоимость всей произведенной за день продукции равна rx + 2ry = r(x + 2y). Целью производства является получение максимальной выручки. Будем рассматривать записанное выражение как функцию от x, y: F(x, y) = r(x + 2y). Поскольку r — константа, то максимальное значение F(x, y) будет достигнуто при максимальной величине выражения x + 2y. Поэтому в качестве функции, максимум которой соответствует стратегической цели, можно принять

f(x, y) = x + 2y ()

Следовательно, получение оптимального плана свелось к следующей математической задаче: найти значения плановых показателей x и y, удовлетворяющих системе неравенств () и придающих максимальное значение целевой функции ().

Методические рекомендации

Приведенный выше пример относится к классу задач линейного программирования. В теории оптимального планирования существует несколько классов задач, из которых линейное программирование — самый простой вариант. Изучение математических методов решения таких задач выходит за рамки целей школьного образования.

Вместе с тем было бы не логично ограничиться лишь теоретической постановкой задач оптимального планирования. Современные информационные технологии позволяют решать некоторые задачи оптимального планирования (и, в частности, линейного программирования) без проникновения в существо применяемых математических методов. В частности, такие средства имеются в табличном процессоре Excel, и на их основе можно продемонстрировать ученикам приемы решения конкретных задач. Средство, о котором идет речь, называется Поиск решения. Соответствующая команда находится в меню Сервис. Опишем кратко, как воспользоваться указанным средством для решения поставленной выше задачи.

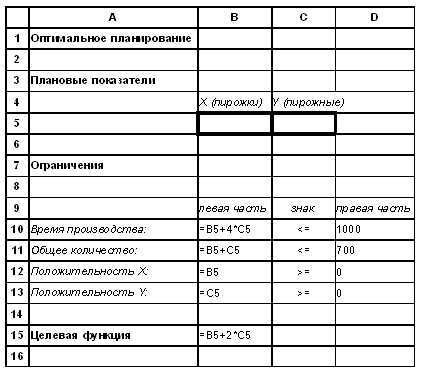
Вначале подготовим таблицу к решению задачи оптимального планирования.

Ячейки B5 и C5 зарезервированы, соответственно, для значений x (план по изготовлению пирожков) и y (план по изготовлению пирожных). Левые части неравенств в столбце В, правые — в столбце D; знаки “ =D12; B13>=D13. Ограничения вводятся следующим образом:

· щелкнуть по кнопке “Добавить”;

· в появившемся диалоговом окне “Добавление ограничения” вводим ссылку на ячейку В10, выбираем из меню знак неравенства “ Зависимость скорости падения от времени с учетом сопротивления воздуха

Заметим, что установившееся предельное значение скорости можно вычислить аналитически, не прибегая к численным методам. Приравняв в формуле (6) dv/dt (ускорение) к нулю, получим, что установившаяся скорость будет равна

и далее не будет возрастать.

На основании данной модели можно, например, решать задачу оптимизации, сформулировав условие так: парашютист прыгает с некоторой высоты и летит, не открывая парашюта; на какой высоте (или через какое время) ему следует открыть парашют, чтобы иметь к моменту приземления безопасную скорость? Другая задача: как связана высота прыжка с площадью поперечного сечения парашюта (входящей в k₂), чтобы скорость приземления была безопасной?

Существенной проблемой при использовании описанного численного метода является выбор величины шага по времени t. От этой величины зависит точность получаемых результатов, устойчивость вычислительной процедуры. Все эти проблемы исследуются в математической дисциплине, которая называется “Численные методы”, или “Вычислительная математика”.

Методические рекомендации

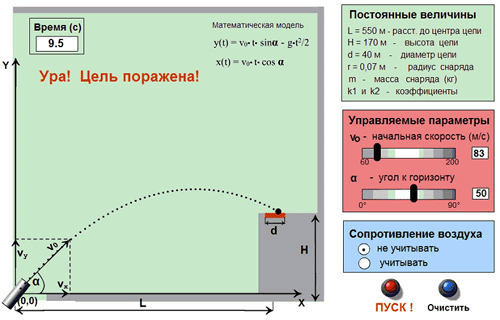
Знакомство учащихся с компьютерными моделями физических процессов в базовом курсе информатики может происходить на уровне демонстрационных примеров. На рисунке показан пример учебной демонстрационной программы, моделирующей полет снаряда, выпущенного из пушки. Задача, которая ставится перед учениками, заключается в подборе параметров (начальной скорости и угла выстрела), которые обеспечивают попадание снаряда в цель (данная программа включена в федеральную коллекцию цифровых образовательных ресурсов). Аналогичные разработки имеются и в других учебных источниках.

Полет снаряда, выпущенного из пушки

В старших классах физико-математического профиля вопросы моделирования физических процессов должны входить в программу профильной подготовки. Можно предложить следующий перечень объектов моделирования, связанных с движением тел:

· движение тел с учетом сопротивления среды (свободное падение, движение тела, брошенного под углом к горизонту, взлет ракеты и др.);

· колебательное движение маятника с учетом сопротивления среды, вынужденные колебания, резонанс и т.д.;

· движение небесных тел (задача двух тел);

· движение заряженных частиц в электрических полях.

Другие типы задач, на базе которых можно реализовывать моделирование физических процессов, связаны с описанием физических процессов в приближении сплошной среды и в электромагнитных полях:

· моделирование процесса теплопроводности и др.;

· моделирование распределений статических — электрического и магнитного — полей.

Выше был подробно разобран пример моделирования свободного падения тела в атмосфере, в котором используются дифференциальные уравнения и численные методы их решения. Если математической подготовки учеников недостаточно для понимания такого подхода, то можно построить математическую модель сразу в конечно-разностной форме, не используя дифференциальных уравнений. Продемонстрируем методику применения такого подхода.

Напомним ученикам, что ускорение есть приращение скорости за единицу времени, а скорость — приращение перемещения за единицу времени: .

Знаки приближенного равенства свидетельствуют о том, что эти соотношения тем точнее, чем меньше промежуток t; в пределе t 0 они становятся точными.

Если в некоторый момент времени t₀ величина s имеет значение s(t₀), а величина v — значение v(t₀), то в последующий момент времени t₁ = t₀ + t будем иметь:

При этом предполагается, что ускорение в течение данного отрезка времени не изменялось и оставалось равным a(t₀). Здесь также использованы обозначения F₀ = F(t₀), m = m(t₀), т.е. имеется в виду, что сила и масса в общем случае могут быть переменными величинами.

При вычислениях значений v и s в последующие моменты времени можно поступать аналогично. Если известны значения v_i и s_i в момент t_i, то

Таким образом, получены те же самые формулы метода Эйлера, но методически иначе. При этом вообще не упоминаются дифференциальные уравнения.

При построении этой и подобной ей моделей следует обратить внимание учащихся на то, что в разбиении непрерывного времени на отрезки длиной t проявляется одна из фундаментальных идей информатики об универсальности дискретной формы представления информации, отраженная как в конструкции компьютера, так и во множестве приложений информатики.

Отметим, что существует немало компьютерных программ, моделирующих простые физические процессы. В них реализован диалоговый интерфейс, позволяющий вводить параметры, получать на экране таблицы, графики, движущиеся изображения. Однако при их использовании остаются скрытыми физические законы, определяющие процесс, ограничения модели, возможности ее усовершенствования. Такие программы полезны скорее как иллюстративные, ознакомительные. Учащихся, изучающих информатику на профильном уровне, целесообразно ориентировать на подробный анализ математических моделей и самостоятельную разработку программ.

Источник