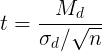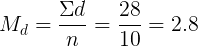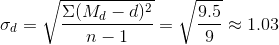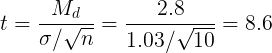Для чего используется коэффициент стьюдента в физике

Для чего используется коэффициент стьюдента в физике

Для уменьшения влияния случайных ошибок необходимо произвести измерение данной величины несколько раз. Предположим, что мы измеряем некоторую величину x. В результате проведенных измерений мы получили значений величины :

Так как оценочные значения результата измерений и ошибки Δx не являются точными, запись (3) результата измерений должна сопровождаться указанием его надежности P. Под надежностью или доверительной вероятностью понимают вероятность того, что истинное значение измеряемой величины заключено в интервале, указанном записью (3). Сам этот интервал называется доверительным интервалом.

Например, измеряя длину некоторого отрезка, окончательный результат мы записали в виде

Таким образом, задача заключается в том, чтобы, имея выборку (2), найти оценку результата измерений , его ошибку Δx и надежность P.

Эта задача может быть решена с помощью теории вероятностей и математической статистики.

В большинстве случаев случайные ошибки подчиняются нормальному закону распределения, установленного Гауссом. Нормальный закон распределения ошибок выражается формулой

где Δx – отклонение от величины истинного значения;

σ – истинная среднеквадратичная ошибка;

σ 2 – дисперсия, величина которой характеризует разброс случайных величин.

Поскольку кривая распределена симметрично относительно оси ординат, можно утверждать, что равные по величине, но противоположные по знаку ошибки равновероятны. А это дает возможность в качестве оценки результатов измерений взять среднее значение всех элементов выборки (2)

где – n число измерений.

Итак, если в одних и тех же условиях проделано n измерений, то наиболее вероятным значением измеряемой величины будет ее среднее значение (арифметическое). Величина стремится к истинному значению μ измеряемой величины при n → ∞.

Средней квадратичной ошибкой отдельного результата измерения называется величина

Она характеризует ошибку каждого отдельного измерения. При n → ∞ S стремится к постоянному пределу σ

С увеличением σ увеличивается разброс отсчетов, т.е. становится ниже точность измерений.

Среднеквадратичной ошибкой среднего арифметического называется величина

Это фундаментальный закон возрастания точности при росте числа измерений.

Ошибка характеризует точность, с которой получено среднее значение измеренной величины . Результат записывается в виде:

Эта методика расчета ошибок дает хорошие результаты (с надежностью 0.68) только в том случае, когда одна и та же величина измерялась не менее 30 – 50 раз.

В 1908 году Стьюдент показал, что статистических подход справедлив и при малом числе измерений. Распределение Стьюдента при числе измерений n → ∞ переходит в распределение Гаусса, а при малом числе отличается от него.

Для расчета абсолютной ошибки при малом количестве измерений вводится специальный коэффициент, зависящий от надежности P и числа измерений n, называемый коэффициентом
Стьюдента t.

Опуская теоретические обоснования его введения, заметим, что

где Δx – абсолютная ошибка для данной доверительной вероятности;
– среднеквадратичная ошибка среднего арифметического.

Для этого удобнее воспользоваться таблицей 3, в которой интервалы заданы в долях величины σ, являющейся мерой точности данного опыта по отношению к случайным ошибкам.

Таблица 2

Таблица 3

При обработке результатов прямых измерений предлагается следующий порядок операций:

Рассмотрим на числовом примере применение приведенных выше формул.

Пример. Измерялся микрометром диаметр d стержня (систематическая ошибка измерения равна 0.005 мм ). Результаты измерений заносим во вторую графу таблицы, находим и в третью графу этой таблицы записываем разности , а в четвертую – их квадраты (таблица 4).

Таблица 4

Задавшись надежностью P = 0.95, по таблице коэффициентов Стьюдента для шести измерений найдем t = 2.57. Абсолютная ошибка найдется по формуле (10).

Сравним случайную и систематическую ошибки:

следовательно, δ = 0.005 мм можно отбросить.

Источник

Основные статистики и t-критерий Стьюдента

В ходе рассмотрения примера мы будем использовать вымышленные сведения, чтобы читатель мог провести необходимые преобразования самостоятельно.

Так, допустим, в ходе исследований изучали влияние препарата А на содержание вещества В (в ммоль/г) в ткани С и концентрацию вещества D в крови (в ммоль/л) у пациентов, разделенных по какому-то признаку Е на 3 группы равного объема (n = 10). Результаты такого выдуманного исследования приведены в таблице:

исходное содержание в крови

Хотим вас предупредить, что выборки объема 10 рассматриваются нами для простоты представления данных и вычислений, на практике такого объема выборок обычно оказывается недостаточно для формирования статистического заключения.

В качестве примера рассмотрим данные 1-го столбца таблицы.

Описательные статистики

Выборочное среднее

Формула для определения среднего арифметического наблюдений (произносится «икс с чертой»):

= (12 + 13 + 14 + 15 + 14 + 13 + 13 + 10 + 11 + 16) / 10 = 13,1;

Выборочная дисперсия

Выборочная дисперсия данного показателя равна s 2 = 3,2.

Среднеквадратичное отклонение

Стандартное (среднеквадратичное) отклоне­ние — это положительный квадратный корень из дисперсии. На примере n наблюдений это выглядит следующим образом:

Мы можем представить себе стандартное отклоне­ние как своего рода среднее отклонение наблюдений от среднего. Оно вычисляется в тех же единицах (размерностях), что и исходные данные.

Коэффициент вариации

Если разделить стандартное отклонение на сред­нее арифметическое и выразить результат в процен­тах, то получится коэффициент вариации.

CV = (1,79 / 13,1) * 100% = 13,7

Ошибка выборочного среднего

1,79 / sqrt (10) = 0,57 [sqrt (x)- функция извлечения квадратного корня из х];

Коэффициент Стьюдента t (одновыборочный t-критерий)

Применяется для проверки гипотезы об отличии среднего значения от некоторого известного значения m

Количество степеней свободы рассчитывается как f=n-1.

В данном случае доверительный интервал для среднего заключен между границами 11,87 и 14,39.

Для уровня доверительной вероятности 95% m=11,87 или m=14,39, то есть= |13,1-11,82| = |13,1-14,38| = 1,28

Диалог Основные статистики и таблицы

В модуле Основные статистики и таблицы выберем Описательные статистики.

Откроется диалоговое окно Описательные статистики.

В поле Перменные выберем Группу 1.

Нажав на Ок, получим таблицы результатов с описательными статистиками выбранных переменных.

Чтобы посчитать t-критерий Стьюдента, в модуле Основные статистики и таблицы выберем Одновыборочный t-критерий.

Откроется диалоговое окно Одновыборочный t-критерий.

Предположим, нам известно, что среднее содержание вещества B в ткани С равно 11.

Таблица результатов с описательными статистиками и t-критерием Стьюдента выглядит следующим образом:

Нам пришлось отвергнуть гипотезу о том, что среднее содержание вещества В в ткани С равно 11.

Так как вычисленное значение критерия больше табличного (2,26), нулевая гипотеза отвергается на выбранном уровне значимости, и различия между выборкой и известной величиной признаются статистически значимыми. Таким образом, вывод о существовании различий, сделанный с помощью критерия Cтьюдента, подтверждается с помощью данного метода.

Выводы

Статистики и процедуры, включенные в одноименный модуль, условно называются основными статистиками и рассматриваются в одной группе, т.к. обычно они используются совместно, особенно на начальной, разведочной стадии анализа данных. Эти статистики являются базовыми и полезны для самых разнообразных исследований. Вычисление описательных статистик является неотъемлемой частью любого статистического анализа.

Источник

Библиотека постов MEDSTATISTIC об анализе медицинских данных

Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic

Критерии и методы

ПАРНЫЙ t-КРИТЕРИЙ СТЬЮДЕНТА

– одна из модификаций метода Стьюдента, используемая для определения статистической значимости различий парных (повторных) измерений.

Уильям Госсет

1. История разработки t-критерия

t-критерий был разработан Уильямом Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны, статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).

2. Для чего используется парный t-критерий Стьюдента?

3. В каких случаях можно использовать парный t-критерий Стьюдента?

Основным условием является зависимость выборок, то есть сравниваемые значения должны быть получены при повторных измерениях одного параметра у одних и тех же пациентов.

Как и в случае сравнения независимых выборок, для применения парного t-критерия необходимо, чтобы исходные данные имели нормальное распределение. При несоблюдении этого условия для сравнения выборочных средних должны использоваться методы непараметрической статистики, такие как G-критерий знаков или Т-критерий Вилкоксона.

Парный t-критерий может использоваться только при сравнении двухвыборок. Если необходимо сравнить три и более повторных измерений, следует использовать однофакторный дисперсионный анализ (ANOVA) для повторных измерений.

4. Как рассчитать парный t-критерий Стьюдента?

Парный t-критерий Стьюдента рассчитывается по следующей формуле:

5. Как интерпретировать значение t-критерия Стьюдента?

Интерпретация полученного значения парного t-критерия Стьюдента не отличается от оценки t-критерия для несвязанных совокупностей. Прежде всего, необходимо найти число степеней свободы f по следующей формуле:

После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p

3. Найдем среднее квадратическое отклонение разностей от средней по формуле:

4. Рассчитаем парный t-критерий Стьюдента:

Источник

Для чего используется коэффициент стьюдента в физике

Критерий t Стьюдента направлен на оценку различий величин средних и двух выборок X и Y, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у связных и несвязных выборок, причем выборки могут быть не равны по величине.

Рассмотрим сначала равночисленные выборки. В этом случае n1 = n2 = n, тогда выражение (9.2) будет вычисляться следующим образом:

В обоих случаях подсчет числа степеней свободы осуществляется по формуле:

где n1 и n2 соответственно величины первой и второй выборки.

Пример : Психолог измерял время сложной сенсомоторной реакции выбора

(в мс) в контрольной и экспериментальной группах. В экспериментальную группу (X) входили 9 спортсменов высокой квалификации. Контрольной группой (Y) являлись 8 человек, активно не занимающихся спортом. Психолог проверяет гипотезу о том, что средняя скорость сложной сенсомоторной реакции выбора у спортсменов выше, чем эта же величина у людей, не занимающихся спортом.

Результаты эксперимента представим в виде табл. 9, в которой произведем ряд необходимых расчетов:

Разница по абсолютной величине между средними

Подсчет выражения дает:

Число степеней свободы = 9 + 8-2= 15. По табл. 17 приложения 6 для данного числа степеней свободы находим :

Строим «ось значимости»:

Таким образом, обнаруженные психологом различия между экспериментальной и контрольной группами значимы более чем на 0,]% уровне, или, иначе говоря, средняя скорость сложной сенсомоторной реакции выбора в группе спортсменов существенно выше, чем в группе людей, активно не занимающихся спортом.

Вычисления значений осуществляется по формуле:

В свою очередь вычисляется по следующей формуле:

Пример: Психолог предположил, что в результате научения время решения эквивалентных задач «игры в 5» (т. е. имеющих один и тот же алгоритм решения) будет значимо уменьшаться. Для проверки гипотезы у восьми испытуемых сравнивалось время решения (в минутах) первой и третьей задач. Решение задачи представим в виде табл. 10.

Вначале произведем расчет по формуле:

Затем применим формулу:

И, наконец, следует применить формулу. Получим:

Строим «ось значимости»:

Измерение может быть проведено в шкале интервалов и отношений.

Сравниваемые выборки должны быть распределены по нормальному закону.

Источник