Для чего используется коническая проекция
Коническая проекция
В конической проекции изображение строится на боковой поверхности конуса, секущего земной шар по двум параллелям или касательного к нему. Вершина конуса лежит на продолжении земной оси.
Параллели нормальной сетки являются дугами концентрических окружностей, а меридианы — их радиусами, углы между которыми пропорциональны соответствующим разностям долгот.
Искажения не зависят от долготы.
В равноугольной конической проекции меридианы сетки растянуты в такой же степени, в какой растянуты ее параллели.
Ссылки
Полезное
Смотреть что такое «Коническая проекция» в других словарях:
коническая проекция — Картографическая проекция, в которой параллели изображаются дугами концентрических окружностей, а меридианы – прямыми, расходящимися из общего центра параллелей, углы между которыми равны разностям их долгот. → Рис. 67 … Словарь по географии
коническая проекция — kūginė projekcija statusas T sritis fizika atitikmenys: angl. conic projection; conical projection vok. Kegelprojektion, f; konische Projektion, f rus. коническая проекция, f pranc. projection conique, f … Fizikos terminų žodynas
коническая картографическая проекция — коническая проекция Картографическая проекция, в которой параллели нормальной сетки дуги концентрических окружностей, а меридианы их радиусы, углы между которыми пропорциональны соответствующим разностям долгот. [ГОСТ 21667 76] Тематики… … Справочник технического переводчика
Проекция Альберса — … Википедия
Равновеликая проекция — Равновеликая проекция. Равновеликая проекция один из основных типов картографических проекций. Не искажает площадей и сохраняет на всей карте единый масштаб площадей, благодаря чему площади фигур на карте пропорциональны площадям… … Википедия
КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ — отображение всей поверхности земного эллипсоида или какой либо ее части на плоскость, получаемое в основном с целью построения карты. К. п. чертят в определенном масштабе. Уменьшая мысленно земной эллипсоид в Мраз, получают его геометрич. модель… … Математическая энциклопедия
легенда к географическим картам — НАСЕЛЕННЫЕ ПУНКТЫ :: более 1 млн. жителей :: от 250 тыс. до 1 млн. жителей :: от 100 тыс. до 250 тыс. жителей :: менее 100 тыс. жителей Прописными буквами выделены столицы. ПУТИ СООБЩЕНИЯ :: Железные дороги … Географическая энциклопедия
Карты географические — (истор.) Первоначальное понятие о К. можно встретить даже у дикарей, особенно живущих по берегам и о вам и имеющих более или менее ясное представление об окружающих их территорию местностях. Путешественники, расспрашивавшие эскимосов С. Америки и … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Картографические проекции. Урок 6
Картографические проекции сегодня – это математические способы изображения всего земного эллипсоида или его части на плоскости, систематическое преобразование широт и долгот с поверхности сферы на плоскость.
Для создания географических карт выполняют две последовательных операции:
При этом картографы пытаются добиться как можно меньшего количества искажений. Сделать мелкомасштабную карту совсем без искажений невозможно. На крупномасштабных (топографических) картах искажения почти отсутствуют. В зависимости от назначения карты одни погрешности допустимы, другие нет. Поэтому и существуют разные типы проекций, предназначенные для сохранения некоторых свойств сферы за счёт других её свойств.

Виды искажений при использовании картографических проекций
Разложить на плоскости эллипс или шар очень трудно, для того, чтобы убедиться в этом, можно попробовать это сделать на практике. Сложить кусочки апельсиновой кожуры так, чтобы между ними не было пустых мест и попробовать получить непрерывную ровную плоскость. Корка соберётся в складки, она не уложится без промежутков.
При любом способе разложения шара на плоскость присутствует один или несколько типов искажения:
При этом типы искажений взаимозависимы, при уменьшении одного из показателей увеличивается другой. В зависимости от назначения карты, на ней присутствуют места с нулевым искажением, с удалением от него количество искажений увеличивается. Поэтому на карте есть три вида масштаба:
При выборе типа картографической проекции сначала строят изоколы – изолинии, соединяющие точки с одинаковым искажением.

Источник: https://ds04.infourok.ru/uploads/ex/0617/00148bfe-04623ef1/hello_html_329bd6b7.jpg
Типы проекций по характеру искажений
Для разных целей нужны карты с отсутствием тех или иных видов искажений. При помощи разных проекций можно сделать так чтобы на них отсутствовали погрешности либо углов, либо длин, либо площадей. Чем больше искажаются углы, тем меньше искажаются площади и наоборот. По характеру искажений все картографические проекции делят на:
Равноугольные картографические проекции
На картах, построенных по этому типу, нет искажений направлений и углов. Направления на местности совпадают с таковыми на карте, прямые линии на местности остаются прямыми на карте. Они используются для прокладки точных маршрутов и применяется на навигационных и топографических картах.
Зато на них сильно изменены площади объектов Земли и линейный масштаб карты зависит от положения на ней данной точки. Типичный пример равноугольной проекции – цилиндрическая проекция Герхарда Меркатора (Герарда Кремера), созданная ещё в 1569 г и используемая в морской навигации до сих пор. Примером использования Проекции Меркатора является равноугольная проекция Гаусса-Крюгера.
В этой проекции создаются отдельные океанологические, климатические и геофизические карты.

Файл доступен по лицензии: Creative Commons Attribution-Share Alike 3.0 Unported
Равновеликие картографические проекции
Это проекции для построении карт, на которых нет искажения площадей (масштаб площадей имеет везде одну и ту же величину), зато сильно растёт погрешность форм и углов (материки и океаны в высоких широтах сплющиваются). Картами, построенными в равновеликих проекциях, удобно пользоваться для расчета площадей, например типов почв, посадок кукурузы, облесенности материков, загрязнения океана или радиоактивного загрязнения суши и др.
Их применяют для составления климатических, почвенных, геофизических, геологических, зоогеографических, геоботанических, экономических, исторических, этнографических, административных карт.

Произвольные картографические проекции
Углы и площади здесь искажаются, но значительно меньше, чем в предыдущих двух проекциях. Поэтому они наиболее используемы. Произвольные картографические проекции не относятся ни к равновеликим, ни к равноугольным.

Равнопромежуточные картографические проекции
Это тип произвольных картографических проекций. В них масштаб длин одного из главных направлений остаётся неизменным. Пример: прямая азимутальная проекция. Равнопромежуточные проекции используют для создания общегеографических, физических, тектонических, политических и др. видов карт.
Характер искажения всегда входит в общее название проекции (равновеликая азимутальная, равноугольная коническая, равновеликая цилиндрическая и т.д.).
Интересно,
что д ревнейшей картографической проекцией является гномическая проекция, применённая на картах звёздного неба Фалесом Милетским ещё в Древней Греции.

Классификация географических проекций по геометрической фигуре, являющейся вспомогательной поверхностью
На плоскость эллипсоид проектируют при помощи геометрических фигур, а поверхности, на которые он проектируется, могут быть секущими (разрезающей) фигуру или касательными (соприкасается, но не разрезает глобус) к ней. При этом на полученной карте касательные и секущие линии (стандартные) представлены неискажёнными.
Проекции также бывают по-разному ориентированы.
Поверхности, которые могут быть развёрнуты на плоскость или лист без растяжений, разрыва или усадки, называются разрабатываемыми поверхностями. Ими являются цилиндр, конус и плоскость. Поэтому по вспомогательной поверхности проекции делятся на:
Полное название проекций может быть следующим: косая азимутальная равновеликая, нормальная равноугольная цилиндрическая, произвольная поликоническая и т.д.
Картографическая коническая проекция: характеристики, достоинства, недостатки
Содержание:
В конических проекциях поверхности Земли меридианы становятся радиальными линиями с центром в вершине и равным угловым интервалом, а параллели Земли становятся дугами окружности, концентричными по отношению к вершине.
На рисунке 1 видно, что коническая проекция не позволяет представить оба полушария. Кроме того, ясно видно, что расстояния искажены в сторону от параллелей, пересекающих конус.
По этим причинам этот тип проекции используется для представления регионов средних широт, протяженных с востока на запад и меньшей протяженности с севера на юг. Так обстоит дело в континентальной части Соединенных Штатов.
Преимущество
Землю можно аппроксимировать сферой с радиусом 6378 км, учитывая, что все массы суши и воды находятся на этой большой сфере. Речь идет о преобразовании этой поверхности, которая покрывает объект в трех измерениях, например, сферу, в другой объект в двух измерениях: плоскую карту. Это приносит недостаток, заключающийся в том, что криволинейная поверхность искажается при ее проецировании на плоскость.
Картографические проекции, такие как коническая проекция, пытаются решить эту проблему с минимальной потерей точности. Следовательно, есть несколько вариантов построения проекции в зависимости от характеристик, которые вы хотите выделить.
Транспортировать глобус повсюду непросто, так как он занимает много места. Также невозможно увидеть всю поверхность Земли сразу, и невозможно воспроизвести все детали на масштабной модели.
Возможны следующие варианты проецирования:
— Проецировать на самолет или
— На цилиндре, который может разворачиваться в прямоугольную плоскость.
— Наконец-то на конусе.
Преимущество конической системы проецирования состоит в том, что она точна по сравнению с параллелями, выбранными для пересечения конуса.
Кроме того, он сохраняет ориентацию по меридианам практически неизменной, хотя может немного исказить шкалу по меридианам для широт, далеких от стандартных или опорных параллелей. Вот почему он подходит для представления очень больших стран или континентов.
Эквидистантная коническая проекция
Это коническая проекционная система, первоначально использовавшаяся Птолемеем, греческим географом, жившим между 100-170 годами нашей эры. Позже в 1745 году его улучшили.
Часто используется в атласах регионов с промежуточными широтами. Он подходит для отображения областей с несколькими градусами широты, принадлежащих одному из экваториальных полушарий.
В этой проекции расстояния истинны по меридианам и по двум стандартным параллелям, то есть параллелям, выбранным для пересечения с конусом проекции.
В эквидистантной конической проекции точка на сфере проходит радиально до пересечения с касательным или секущим конусом, принимая центр сферы за центр проекции.
Недостатки
Основным недостатком конической проекции является то, что она неприменима к экваториальным областям.
Кроме того, коническая проекция не подходит для картографирования больших регионов, а скорее отдельных областей, таких как Северная Америка.
Коническая проекция Альберта
Используйте две стандартные параллели и сохраните площадь, но не масштаб и форму. Этот тип конического выступа был введен Х. К. Альберсом в 1805 году.
Все области на карте пропорциональны земным. В ограниченных регионах направления относительно точны. Расстояния соответствуют расстояниям от сферической поверхности на стандартных параллелях.
В Соединенных Штатах эта система проекции используется для карт, показывающих границы штатов Союза, для которых 29,5º с.ш. и 45,5º с.ш. выбраны в качестве стандартных параллелей, что приводит к максимальной ошибке шкалы в 1, 25%.
Карты, сделанные с помощью этой проекции, не сохраняют углы, соответствующие углам сферы, а также перспективу или равноудаленность.
Конформная коническая проекция Ламберта
Он был предложен в 1772 году одноименным швейцарским математиком и географом. Его основная характеристика заключается в том, что он использует касательный или секущий конус к сфере, а проекция сохраняет неизменными углы. Эти качества делают его очень полезным в аэронавигационных картах.
Геологическая служба США (USGS) использует проекцию конуса Ламберта. В этой проекции расстояния истинны по стандартным параллелям.
В конической проекции Ламберта направления остаются достаточно точными. Области и формы слегка искажаются в положениях, близких к стандартным параллелям, но изменение формы и площади увеличивается с расстоянием между ними.
Поскольку целью этой проекции является поддержание направлений и углов, равных исходным на сфере или эллипсоиде, не существует геометрического метода их получения, в отличие от эквидистантной проекции Птолемея.
Скорее, это метод аналитического проектирования, основанный на математических формулах.
Базовые карты USGS для 48 континентальных штатов используют 33º и 45º с.ш. в качестве стандартных параллелей, что дает максимальную ошибку карты в 2,5%.
Для навигационных карт на Аляске используются базовые параллели: 55 ° и 65 °. Вместо этого в национальном атласе Канады используются 49º и 77º северной широты.
Конические проекции.
Основные виды картографических проекций.
В авиации карты используются как при подготовке к полету, так и в процессе полета. При подготовке к полету карта необходима для прокладки и изучения маршрута полета; измерения путевых углов и расстояний между пунктами маршрута; определения географических координат пунктов; нанесения точек расположения радиотехнических средств, обеспечивающих полет; получения данных о магнитном склонении в районе полета; изучения рельефа местности.
В полете карта применяется для ведения визуальной и радиолокационной ориентировки; контроля пути и прокладки линий положения самолета; определения навигационных элементов полета.
Карты нужны также службе движения для руководства полетами и контроля за их выполнением. Авиационные карты создаются в определенных картографических проекциях.
Картографической проекцией называется способ изображения земной поверхности на плоскости. Сущность любой картографической проекции состоит в том, что поверхность земного шара переносится сначала на глобус определенного размера, а затем с глобуса по намеченному способу на плоскость.
При переносе поверхности Земли с глобуса на плоскость приходится в одних местах растягивать изображения, а в других сжимать, т.е. допускать искажения. Каждая проекция имеет определенную степень искажения длин, направлений и площадей и определенный вид сетки меридианов и параллелей. Выбор проекции для построения карты зависит от того, каким требованиям должна отвечать данная карта.
По виду сетки меридианов и параллелей все картографические проекции делятся на конические (поликонические) цилиндрические, и азимутальные.
Конические проекции.
Конические проекции могут строиться на касательном или секущем конусе.
В зависимости от расположения оси конуса относительно оси вращения глобуса конические проекции могут быть нормальные, поперечные и косые. Большинство авиационных карт конической проекции построено в нормальной равноугольной проекции на касательном или секущем конусах.
Равноугольная коническая проекция на касательном конусе. Построение этой проекции (рис. 1) наглядно можно объяснить следующим образом. Все меридианы выпрямляют до соприкосновения с боковой поверхностью конуса. При этом все параллели, кроме параллели касания, будут растягиваться до размеров окружности конуса. Для того чтобы сделать проекцию равноугольной и сохранить подобие фигур,
Рисунок 1. Равноугольная коническая проекция на касательном конусе
производят растягивание меридианов в такой степени, в какой были растянуты параллели в данной точке карты. Затем конус разрезается по образующей и разворачивается на плоскость. Карты в равноугольной конической проекции на касательном конусе имеют следующие свойства:
— меридианы изображаются в виде прямых, сходящихся к полюсу;
— угол схождения меридианов определяется по формуле
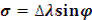
— параллели имеют вид дуг концентрических окружностей, расстояния между которыми увеличиваются по мере удаления от параллели касания;
— на параллели касания искажения длин отсутствуют, а в полосе ±5° от этой параллели они незначительны и в практике не учитываются;
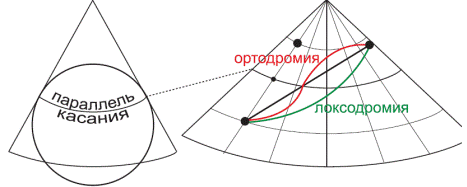
— локсодромия изображается кривой линией, обращенной своей выпуклостью к экватору;
— ортодромия для расстояний до 1200 км изображается прямой линией, а для больших расстояний имеет вид кривой, обращенной своей выпуклостью в сторону более крупного масштаба.
В равноугольной конической проекции на касательном конусе издаются бортовые карты масштабов 1:2000000; 1:2500000; 1:3000000; 1:4000000 и обзорная карта масштаба 1:5000000.
Рисунок 2. Равноугольная коническая проекция на секущем конусе
Справка
Самая простая коническая проекция проходит по касательной к глобусу вдоль линии широты. Эта линия называется стандартной параллелью. Меридианы проецируются на коническую поверхность, сходясь на вершине или в точке конуса. Параллели проецируются на коническую поверхность как кольца. Конус затем “рассекается” вдоль любого меридиана для создания конечной конической проекции, в которой имеются прямые сходящиеся меридианы и параллели, представленные концентрическими окружностями. Меридиан, противолежащий линии сечения, становится центральным меридианом.
В целом, чем дальше от стандартной параллели, тем больше искажение. Соответственно, отсечение верхушки конуса создает более точную проекцию. Этого можно достичь, если не использовать полярную область при проецировании объектов. Конические проекции используются для среднеширотных зон, имеющих ориентацию с востока на запад.
Более сложные конические проекции соприкасаются с поверхностью глобуса в двух местах. Эти проекции называются секущими коническими проекциями и определяются двумя стандартными параллелями. Можно также определить секущую проекцию с помощью одной стандартной параллели и коэффициента масштабирования. Характер искажений при секущих проекциях различается для районов, расположенных между стандартными параллелями, и для районов, расположенных за их пределами. Как правило, секущая проекция дает меньшее суммарное искажение, чем касательная проекция. В еще более сложных конических проекциях ось конуса не совпадает с полярной осью глобуса. Такие проекции называются косыми.
Изображение географических объектов зависит от расстояния между параллелями. При их равном удалении друг от друга проекция получается равнопромежуточной в направлении с севера на юг, но не равноугольной и не равновеликой. Примером такого типа проекций является Равнопромежуточная Коническая проекция. Для небольших областей общее искажение минимально. В равноугольной конической проекции Ламберта расстояние между центральными параллелями меньше, чем у параллелей ближе к границам, и не искажаются формы малых географических объектов на мелкомасштабных и крупномасштабных картах. В равновеликой конической проекции Альберса параллели вблизи северного и южного полюса расположены ближе друг к другу, чем центральные параллели, и проекция отображает эквивалентные площади.