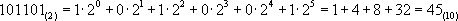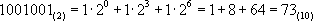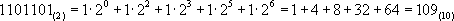Для чего используется целочисленный формат
Урок №31. Целочисленные типы данных: short, int и long
Обновл. 11 Сен 2021 |
На этом уроке мы рассмотрим целочисленные типы данных в языке С++, их диапазоны значений, операцию деления, а также переполнение (что это такое и примеры).
Целочисленные типы данных
| Тип | Минимальный размер | |
| Символьный тип данных | char | 1 байт |
| Целочисленный тип данных | short | 2 байта |
| int | 2 байта (но чаще всего 4 байта) | |
| long | 4 байта | |
| long long | 8 байт |
Примечание: Тип char — это особый случай: он является как целочисленным, так и символьным типом данных. Об этом детально мы поговорим на одном из следующих уроков.
Основным различием между целочисленными типами, перечисленными выше, является их размер, чем он больше, тем больше значений сможет хранить переменная этого типа.
Объявление целочисленных переменных
Объявление происходит следующим образом:
Диапазоны значений и знак целочисленных типов данных
Как вы уже знаете из предыдущего урока, переменная с n-ным количеством бит может хранить 2 n возможных значений. Но что это за значения? Это значения, которые находятся в диапазоне. Диапазон — это значения от и до, которые может хранить определенный тип данных. Диапазон целочисленной переменной определяется двумя факторами: её размером (измеряется в битах) и её знаком (который может быть signed или unsigned).
Целочисленный тип signed (со знаком) означает, что переменная может содержать как положительные, так и отрицательные числа. Чтобы объявить переменную как signed, используйте ключевое слово signed :
По умолчанию, ключевое слово signed пишется перед типом данных.
В некоторых случаях мы можем заранее знать, что отрицательные числа в программе использоваться не будут. Это очень часто встречается при использовании переменных для хранения количества или размера чего-либо (например, ваш рост или вес не может быть отрицательным).
Целочисленный тип unsigned (без знака) может содержать только положительные числа. Чтобы объявить переменную как unsigned, используйте ключевое слово unsigned :
1-байтовая целочисленная переменная без знака (unsigned) имеет диапазон значений от 0 до 255.
Обратите внимание, объявление переменной как unsigned означает, что она не сможет содержать отрицательные числа (только положительные).
Теперь, когда вы поняли разницу между signed и unsigned, давайте рассмотрим диапазоны значений разных типов данных:
Для нематематиков: Используем таблицу 🙂
Начинающие программисты иногда путаются между signed и unsigned переменными. Но есть простой способ запомнить их различия. Чем отличается отрицательное число от положительного? Правильно! Минусом спереди. Если минуса нет, значит число — положительное. Следовательно, целочисленный тип со знаком (signed) означает, что минус может присутствовать, т.е. числа могут быть как положительными, так и отрицательными. Целочисленный тип без знака (unsigned) означает, что минус спереди отсутствует, т.е. числа могут быть только положительными.
Что используется по умолчанию: signed или unsigned?
Так что же произойдет, если мы объявим переменную без указания signed или unsigned?
| Тип | По умолчанию | |
| Символьный тип данных | char | signed или unsigned (в большинстве случаев signed) |
| Целочисленный тип данных | short | signed |
| int | signed | |
| long | signed | |
| long long | signed |
Все целочисленные типы данных, кроме char, являются signed по умолчанию. Тип char может быть как signed, так и unsigned (но, обычно, signed).
В большинстве случаев ключевое слово signed не пишется (оно и так используется по умолчанию).
Программисты, как правило, избегают использования целочисленных типов unsigned, если в этом нет особой надобности, так как с переменными unsigned ошибок, по статистике, возникает больше, нежели с переменными signed.
Правило: Используйте целочисленные типы signed, вместо unsigned.
Переполнение
Вопрос: «Что произойдет, если мы попытаемся использовать значение, которое находится вне диапазона значений определенного типа данных?». Ответ: «Переполнение».
Переполнение (англ. «overflow») случается при потере бит из-за того, что переменной не было выделено достаточно памяти для их хранения.
На уроке №28 мы говорили о том, что данные хранятся в бинарном (двоичном) формате и каждый бит может иметь только 2 возможных значения ( 0 или 1 ). Вот как выглядит диапазон чисел от 0 до 15 в десятичной и двоичной системах:
| Десятичная система | Двоичная система |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
Как вы можете видеть, чем больше число, тем больше ему требуется бит. Поскольку наши переменные имеют фиксированный размер, то на них накладываются ограничения на количество данных, которые они могут хранить.
Примеры переполнения
Рассмотрим переменную unsigned, которая состоит из 4 бит. Любое из двоичных чисел, перечисленных в таблице выше, поместится внутри этой переменной.
«Но что произойдет, если мы попытаемся присвоить значение, которое занимает больше 4 бит?». Правильно! Переполнение. Наша переменная будет хранить только 4 наименее значимых (те, что справа) бита, все остальные — потеряются.
Например, если мы попытаемся поместить число 21 в нашу 4-битную переменную:
| Десятичная система | Двоичная система |
| 21 | 10101 |
Число 21 занимает 5 бит (10101). 4 бита справа (0101) поместятся в переменную, а крайний левый бит (1) просто потеряется. Т.е. наша переменная будет содержать 0101, что равно 101 (нуль спереди не считается), а это уже число 5, а не 21.
Теперь рассмотрим пример в коде (тип short занимает 16 бит):
Результат выполнения программы:
x was: 65535
x is now: 0
Что случилось? Произошло переполнение, так как мы попытались присвоить переменной x значение больше, чем она способна в себе хранить.
Для тех, кто хочет знать больше: Число 65 535 в двоичной системе счисления представлено как 1111 1111 1111 1111. 65 535 — это наибольшее число, которое может хранить 2-байтовая (16 бит) целочисленная переменная без знака, так как это число использует все 16 бит. Когда мы добавляем 1, то получаем число 65 536. Число 65 536 представлено в двоичной системе как 1 0000 0000 0000 0000, и занимает 17 бит! Следовательно, самый главный бит (которым является 1) теряется, а все 16 бит справа — остаются. Комбинация 0000 0000 0000 0000 соответствует десятичному 0, что и является нашим результатом.
Аналогичным образом, мы получим переполнение, использовав число меньше минимального из диапазона допустимых значений:
Результат выполнения программы:
x was: 0
x is now: 65535
Переполнение приводит к потере информации, а это никогда не приветствуется. Если есть хоть малейшее подозрение или предположение, что значением переменной может быть число, которое находится вне диапазона допустимых значений используемого типа данных — используйте тип данных побольше!
Правило: Никогда не допускайте возникновения переполнения в ваших программах!
Деление целочисленных переменных
В языке C++ при делении двух целых чисел, где результатом является другое целое число, всё довольно предсказуемо:
Но что произойдет, если в результате деления двух целых чисел мы получим дробное число? Например:
В языке C++ при делении целых чисел результатом всегда будет другое целое число. А такие числа не могут иметь дробь (она просто отбрасывается, не округляется!).
Правило: Будьте осторожны при делении целых чисел, так как любая дробная часть всегда отбрасывается.
Поделиться в социальных сетях:
Урок №30. Размер типов данных
Комментариев: 23
Всем доброго времени суток. Появился такой вопрос: для объявления без знакового числа, для плюсов, обязательно писать unsigned int X, есть ли сокращенная форма по типу uint X?
Может проще для запоминания было сказать, что тип signed (со знаком) использует 1 (старший бит в байте для записи этого самого знака и для самого числа остается 7 бит (это в случае 1-го байта, для 2- байт 15 и т.д.) и в 7 битах можно записать число не больше чем 128.
К примеру 10000000 это отрицательный ноль. 🙂 Но такого не бывает.
Для того, чтоб числа имели дробь при делении целых чисел можно приписать ноль после точкой. Например : 8.0/5.0 = 1.6
Только это уже совсем другая история)
Достаточно поставить точку одному из выражений. Например: 8. / 5 или 8 / 5.
Остальное компилятор сам подставит)
Вообще, с «железным» правилом «Никогда не допускайте возникновения переполнения в ваших программах!» — сильно погорячились. Потому что очень часто переполнение как раз помогает создать более простой и быстрый код.
Например, нужно много раз увеличивать переменную на 1 и циклически прокручивать все значения от 0 до 255. Писать условие «если равно 255, то присвоить 0» — совсем не нужно, это произойдёт само при прибавлении 1 к 255, если используется 1-байтовая беззнаковая.
Другой очень частый пример: вычисление разности двух значений миллисекундного таймера, чтобы замерить период времени. 4-байтовая переменная с таким таймером переполняется каждые 49 суток. Если система работает непрерывно, то такое может случаться. Когда считаем разность (новое значение таймера минус старое) — возможен случай, когда новое значение уже переполнилось (снова пошло с нуля), а старое ещё нет (огромное число). Но когда вычисляется разность, тут снова произойдёт переполнение (из-за того, что получилось отрицательное значение), и эти два переполнения оказывают взаимно компенсирующее действие, как будто их не было вообще. И разность всё равно будет верной. И не надо городить никаких хитрых алгоритмов.
Скорее всего это какой-то очень древний подход. Никогда не слышал подобного в универе.
Потому что это относится к числам с плавающей точкой. У них отдельный бит хранит знак. В целочисленных типах такого нигде (или почти нигде) нет.
unsigned используется для экономии памяти, это же очевидно. Если знак действительно не нужен за счет дополнительно освобожденного бита, можно увеличить диапазон значений в 2 раза, что в некоторых случаях позволит использовать более «экономные» типы данных.
Ну так нужно указывать другой тип переменной(не целое число). Тогда будет дробь.
Забавная история, почему этот урок так важен =)
В игре Civilization есть баг с механикой агрессии и миролюбия. Суть такова, что агрессивность цивилизации измерялась по шкале от 1 до 10. Девятки и десятки были у всяких Чингисханов, Монтесум и Сталиных, а у духовного пацифиста Махатмы Ганди была единичка. И ещё были модификаторы — строй «республика» уменьшает агрессивность на 1, «демократия» — на 2. Соответственно, сразу же, как только индусы открывали Демократию, у Ганди становилась агрессивность −1.
А теперь внимание. Эта переменная была однобайтная и строго неотрицательная(unsigned), от 0 до 255. Соответственно, агрессивность Махатмы Ганди становилась равна 255 из 10. Поэтому, построив у себя демократию, Ганди двигался рассудком, клепал ядрёные бомбы и умножал всех на ноль.
Действительно хороший пример 🙂 С unsigned нужно быть аккуратным.
Представление чисел в компьютере
После того, как мы узнали об основных единицах для измерения информации необходимо разобраться с тем, как в ЭВМ хранятся различные типы данных. В этой статье мы поговорим про представление чисел в компьютере.
Основные понятия и положения
Прежде чем начать разбираться в теме, следует понимать, что все ЭВМ, на данный момент времени, работают с двоичной системой счисления. Это значит, что и вся информация (звуковая, графическая или текстовая) хранится в памяти ПК в виде последовательностей нулей и единиц.
Схематично компьютерная память выглядит так, как показано на схеме ниже:
Как видно из рисунка внутренняя память представляет собой разряды, каждый из которых содержит один бит информации (0 или 1). А восемь битовых кластеров образуют один байт (машинное слово).
Машинное слово – минимально адресуемая ячейка памяти, которую за раз можно обработать командой процессора. То есть минимально процессор может обработать один байт.
Отсюда также вытекает правило, что данные в компьютере представляются дискретно (отдельно). В качестве примера приведем изображение на мониторе. Оно состоит из точек (пикселей). Цвет же каждой точки задается последовательностью из 0 и 1.
Представление чисел в компьютере
Существует несколько вариантов для отображения чисел в ЭВМ, и зависят они от формата числа.
Представление целых чисел в ЭВМ
Для представления целых чисел, в вычислительных машинах существует несколько способов, которые используют 8,16, 24 или 32 разряда памяти (1, 2, 3 и 4 байта).
Первым способом является беззнаковое представление. С его помощью представляются только целые положительные величины, которые не участвуют в арифметических операциях и выступают в роли констант (дата, время и т.д.).
Чтобы представить число в беззнаковой форме необходимо перевести его в двоичную систему счисления и дополнить с начала нулями до нужной разрядности (дополняем до 1,2,3 или 4 байт).
Также следует отметить, что есть ограничения на количество чисел, которые можно представить в n разрядной ячейке. Для беззнаковых величин оно составляет \( 2^n \).
Пример: Перевести 54 в беззнаковый формат.
Находим представление 54 в бинарной системе счисления:
\( 1) \ 54:2 \ = \ 27 \ | \ Остаток \ 0 \)
\( 2) \ 27:2 \ = \ 13 \ | \ Остаток \ 1 \)
\( 3) \ 13:2 \ = \ 6 \ | \ Остаток \ 1 \)
\( 4) \ 6:2 \ = \ 3 \ | \ Остаток \ 0 \)
\( 5) \ 3:2 \ = \ 1 \ | \ Остаток \ 1 \)
Итого \( 54_ <10>\) равняется \( 110110_ <2>\).
Дополняем результат до одной из стандартных разрядностей (8 бит) = 00110110.
Ответ: 00110110.
Для представления чисел, которые участвуют в вычислительных операциях, используется представление со знаком. В такой форме записи старший разряд всегда отводится под знак (0 для положительных чисел и 1 для отрицательных).
В случае со знаковым представлением также существуют ограничения. Так как один разряд отводится под знак, то в n-разрядную ячейку можно записать \( (2^
Также следует отметить следующую особенность — все отрицательные значения в компьютере хранятся в обратном или дополнительном коде, а положительные в прямом.
Для того чтобы перевести число в обратный и дополнительный код вам надо:
Почему же для хранения отрицательных чисел используют обратный или дополнительный код? Это позволяет изменить операцию вычитания на операцию сложения. В противном случае компьютеру бы каждый раз приходилось выяснять, где положительная величина, а где отрицательная и после этого сравнивать их модули, для определения конечного знака, что очень сильно усложняло бы весь алгоритм.
Представление вещественных чисел
Всего существует два способа для представления множества вещественных значений – естественная или экспоненциальная форма.
В жизни мы пользуемся естественной формой. Так число 42,6 мы можем записать несколькими способами. Например:
В компьютере же используется экспоненциальная форма записи. Выглядит она так:
Здесь m – мантисса, которая представляет собой правильную дробь (в правильных дробях числитель меньше знаменателя).
q – система счисления, в которой представлено число.
P – порядок.
В ЭВМ отводится один разряд под знак мантиссы, один под знак порядка и различное число бит под саму мантиссу и порядок. Данный формат записи называется «С плавающей запятой».
Чем больше бит отводится под мантиссу, тем точнее представляемая величина, чем больше ячеек отводится под порядок, тем шире диапазон от наименьшего числа, до наибольшего числа, представляемого в компьютере при заданном формате.
Так как компьютерная память величина дискретная и конечная, то и множество вещественных чисел, с которым работает ЭВМ также конечно.
Видео
Заключение
Вот мы и разобрались с представлением чисел в компьютере и информатике. Краткий материал из данной статьи вы можете использовать для своей онлайн-презентации. При возникновении вопросов оставляйте их в комментариях.
Способы представления чисел в разрядной сетке ЭВМ
Для хранения чисел в памяти компьютера используется два формата: целочисленный (естественная форма) и с плавающей точкой (нормализованная форма) (точка — разделительный знак для целой и дробной части числа).
Целочисленный формат (формат с фиксированной точкой) используется для представления в компьютере целых (англ. integer) положительных и отрицательных чисел. Для этого, как правило, используются форматы, кратные байту: 1, 2, 4 байта.
В форме с фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой (или точки), отделяющей целую часть от дробной.
Эта форма проста и привычна для большинства пользователей, но имеет небольшой диапазон представления чисел и поэтому не всегда пригодна при вычислениях. Если же в результате какой-либо арифметической операции получается число, выходящее за допустимый диапазон, то происходит переполнение разрядной сетки, и все дальнейшие вычисления теряют смысл.
Однобайтовое представление применяется только для положительных целых чисел. В этом формате отсутствует знаковый разряд. Наибольшее двоичное число, которое может быть записано при помощи 1 байта, равно 11111111, что в десятичной системе счисления соответствует числу 25510.
Самое большое (по модулю) целое число со знаком, которое может поместиться в 2-байтовом формате, это число 0111111111111111, то есть при помощи подобного кодирования можно представить числа от −32 76810 до 32 76710.
Если число вышло за указанные границы, произойдет переполнение! Поэтому при работе с большими целыми числами под них выделяется больше места, например 4 байта.
Формат с плавающей точкой (нормализованная форма) используется для представления в компьютере действительных чисел (англ. real). Числа с плавающей точкой размещаются, как правило, в 4 или 8 байтах.
Нормализованная форма представления чисел обеспечивает огромный диапазон их записи и является основной в современных ЭВМ.
Представление целого положительного числа в компьютере
Для представления целого положительного числа в компьютере используется следующее правило:
— число переводится в двоичную систему;
— результат дополняется нулями слева в пределах выбранного формата;
— последний разряд слева является знаковым, в положительном числе он равен 0.
Представление целого отрицательного числа в компьютере
Для представления целого отрицательного числа в компьютере используется дополнительный код. Такое представление позволяет заменить операцию вычитания числа операцией сложения с дополнительным кодом этого числа. Знаковый разряд целых отрицательных чисел всегда равен 1.
Для представления целого отрицательного числа в компьютере используется следующее правило:
— к полученному коду прибавляется 1.
Обратный код для положительного двоичного числа совпадает с его прямым кодом, а для отрицательного числа нужно во всех разрядах, кроме знакового, нули заменить единицами и наоборот.
Дополнительный код для положительного числа совпадает с его прямым кодом, а для отрицательного числа образуется путем прибавления 1 к обратному коду.
Отрицательное число может быть представлено в виде 2 или 4 байт.
Например, представим число −13510 в 2-байтовом формате:
— 13510 → 10000111 (перевод десятичного числа без знака в двоичный код);
— 0000000010000111(дополнение двоичного числа нулями слева в пределах формата);
— 0000000010000111 → 1111111101111000(перевод в обратный код);
— 1111111101111000 → 1111111101111001 (перевод в дополнительный код).
Представление вещественного (действительного) числа в компьютере
Вещественное число может быть представлено в экспоненциальном виде, например:
В этом формате вещественное число (R) представляется в виде произведения мантиссы (m) и основания системы счисления (P) в целой степени (n), называемой порядком.
Задания для самостоятельного решения
Задание 1 Получить десятичный эквивалент для двоичных чисел.
Перевод числа из двоичной в десятичную систему счисления выполняется только представлением его в развёрнутой форме.
Варианты заданий для самостоятельного выполнения
Целое (тип данных)
Содержание
Представление
В памяти типовой компьютерной системы целое число представлено в виде цепочки битов фиксированного (кратного 8) размера. Эта последовательность нолей и единиц — ни что иное, как двоичная запись числа, поскольку обычно для представления чисел в современной компьютерной технике используется позиционный двоичный код. Диапазон целых чисел, как правило, определяется количеством байтов в памяти компьютера, отводимых под одну переменную.
Для 64-разрядных операционных систем учитывая разность моделей данных (LP64, LLP64, ILP64), представление целого типа на разных моделях данных может отличаться между собой. Тип int и long может составлять как 4 так и 8 байт.
Стоит отметить, что каждый язык программирования реализует свою сигнатуру представления целых чисел, которая может отличатся от международных стандартов, но обязана его/их поддерживать. К примеру можно отнести кросс-платформенную библиотеку Qt, где целое представляется типом qintX и quintX, где X-8,16,32,64.
Целые типы подразделяются на беззнаковые (англ. unsigned ) и знаковые (англ. signed ).
Беззнаковые целые
В C и C++ для обозначения беззнаковых типов используется префикс unsigned. В C# в качестве показателя беззнаковости используется префикс u (англ. unsigned). Например, для объявления беззнакового целого, равного по размеру одному машинному слову используется тип uint.
Беззнаковые целые, в частности, используются для адресации памяти, представления символов.
Иногда в литературе [1] встречаются рекомендации не использовать тип беззнаковые целые, поскольку он может быть не реализован процессором компьютера, однако вряд ли этот совет следует считать актуальным — большинство современных процессоров (в том числе x86-совместимые [2] ) одинаково хорошо работают как со знаковыми, так и с беззнаковыми целыми.
В некоторых языках, например java, беззнаковые целые типы (за исключением символьного) отсутствуют. [3]
Целые со знаком
Предельные значения для разных битностей
Ниже представлена таблица предельных значений десятичных чисел для разных битностей при кодировании дополнительным кодом. Не зависимо от битности у целых без знака минимальным значением всегда является 0 и поэтому оно не упомянуто. Справа от значения указано количество значащих цифр.
| Бит | Максимальное без знака | Минимальное со знаком | Максимальное со знаком | |||
|---|---|---|---|---|---|---|
| Значение | Цифр | Значение | Цифр | Значение | Цифр | |
| 4 | 15 | 2 | -8 | 1 | 7 | 1 |
| 8 | 255 | 3 | -128 | 3 | 127 | 3 |
| 16 | 65 535 | 5 | -32 768 | 5 | 32 767 | 5 |
| 24 | 16 777 215 | 8 | -8 388 608 | 7 | 8 388 607 | 7 |
| 32 | 4 294 967 295 | 10 | -2 147 483 648 | 10 | 2 147 483 647 | 10 |
| 48 | 281 474 976 710 655 | 15 | -140 737 488 355 328 | 15 | 140 737 488 355 327 | 15 |
| 64 | 18 446 744 073 709 551 615 | 20 | -9 223 372 036 854 775 808 | 19 | 9 223 372 036 854 775 807 | 19 |
| 96 | 79 228 162 514 264 337 593 543 950 335 | 29 | -39 614 081 257 132 168 796 771 975 168 | 29 | 39 614 081 257 132 168 796 771 975 167 | 29 |
| 128 | 340 282 366 920 938 463 463 374 607 431 768 211 455 | 39 | -170 141 183 460 469 231 731 687 303 715 884 105 728 | 39 | 170 141 183 460 469 231 731 687 303 715 884 105 727 | 39 |
Операции над целыми
Арифметические операции
К целочисленным значениям применимы в первую очередь арифметические операции. Ниже приведены самые часто используемые (в скобках указаны их обозначения в различных языках программирования и им аналогичным средствах).
В некоторых языках программирования для лаконичности есть операторы, которые позволяют производить арифметическую операцию с присвоением. Например, «+=» складывает текущее значение переменной слева с выражением справа и помещает результат в исходную переменную. Так же в некоторых языках и средах доступна совмещённая операция MulDiv, которая умножает на одно число, а потом делит результат на второе.
Обычно самыми дорогими по скорости операциями являются умножение и деление (получение остатка от деления).
В памяти компьютера для хранения целых чисел обычно отводится ячейки фиксированного объёма. Из-за этого операции увеличения и уменьшения значений могут приводить к переполнению, что оборачивается искажением результата. Некоторые языки программирования позволяют производит вызов исключения в таких случаях. Кроме этого можно определять поведение при переполнении:
Побитовые операции
Помимо математических, к целым числам применимы битовые операции, которые основаны на особенностях позиционного двоичного кодирования. Обычно они выполняются значительно быстрее арифметических операций и поэтому их используют как более оптимальные аналоги.
Работа со строками
Довольно частыми операциями являются получение строки из числового значения во внутреннем представлении и обратно — число из строки. При преобразовании в строку обычно доступны средства задания форматирования в зависимости от языка пользователя.
Ниже перечислены некоторые из представлений чисел строкой.
Перечислимый тип
К целым относится также перечислимый тип. Переменные перечислимого типа принимают конечный заранее заданный набор значений. Размер набора не определяется числом байтов, используемых для представления целочисленных значений переменных такого типа.