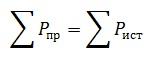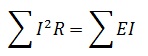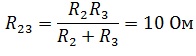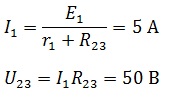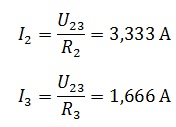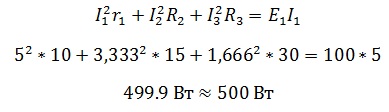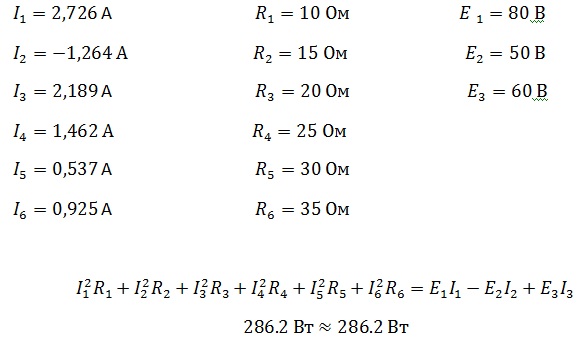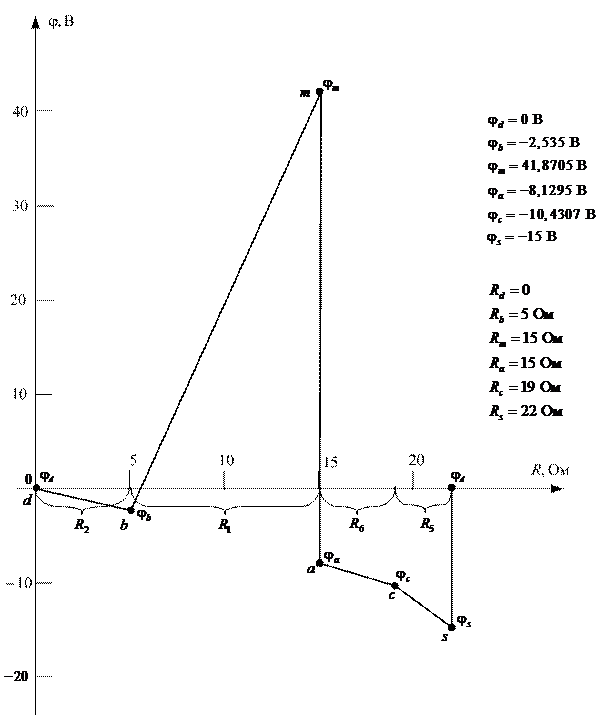Для чего используют баланс мощностей
Баланс мощностей в цепи постоянного тока
Баланс мощностей является следствием закона сохранения энергии — суммарная мощность вырабатываемая (генерируемая) источниками электрической энергии равна сумме мощностей потребляемой в цепи.
Источники E1 и E2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадают (если ЭДС и ток в ветвях направлены в противоположную сторону, то источник ЭДС потребляет энергию и его записывают со знаком минус). Баланс мощностей для заданной цепи запишется так:
С учетом погрешности расчетов баланс мощностей получился.
Какова допустимая погрешность?? У меня выходит 0,561
По идее баланс мощности должен равняться нулю, но так как мы округляем некоторые значения при расчете — возникает погрешность, которая может составлять примерно 0,1 — 5% от потребляемой мощности.
Про знаки ЭДС сказано про знаки мощностей приёмников — нет.
Баланс мощностей электрической цепи
Электрическая цепь предполагает передачу определенной мощности от источника к потребителю. При этом, должно сохраняться равновесие, если схема состоит из сопротивлений, индуктивности. Статья раскроет тему, что такое баланс мощностей в простой цепи переменного тока. Будет описан этот показатель для постоянного напряжения, приведены формулы вычисления.
Определение
Вычисление данного параметра в электрической цепи основано на известном законе сохранения энергии. Из него следует, что мгновенные показатели, передаваемые от источника, должны быть равны сумме значений, которую получают потребители.
Баланс для мощностей представляет собой общеизвестный нам закон сохранения энергии. Выражение данного закона в этом случае — сумма всей энергии от источников (генератора или блока питания) равняется сумме, которую получают приемники.
Можно использовать альтернативный вариант. Для него формула при этом имеет вид как на рисунке ниже:
Стоит принять во внимание, что любая электрическая схема имеет сопротивление. Описываемая величина с сопутствующими значениями рассчитывается с учетом разновидности напряжений. Принимая во внимание закон сохранения энергии, стоит учитывать, что по электрической схеме всегда передается энергия.
Назначение
Составление простого баланса мощностей используют для точного определения расхождений между передаваемой и получаемой энергиями. Также, уравнение баланса мощностей применяется для решения многих электротехнических задач.
Переменный ток
Баланс мощностей в простой цепи переменного тока рассчитывается по более сложной формуле. Баланс мощностей в простой цепи синусоидального тока учитывает комплексные, реактивные и активные параметры.
Главное отличие рассматриваемой величины — это наличие ненаправленного движения переменного тока по проводникам. Параметр такой схемы может быть увеличен или уменьшен (например, генератором), что может повлиять на конечный результат.
Постоянный ток
В электрической цепи постоянного тока напряжение и мощность всегда одного значения. Поэтому сделать вычисление намного проще. Можно сделать расчет на основе достаточно простого примера.
При вычислении параметров этой схемы имеет смысл учесть расход приемника. Резистор при нагреве выделяет тепло, а значит выполняется преобразование электричества в тепло. Беря во внимание физический закон сохранения, тепло выделяемое резистором также будет равно 10 Ватт.
Заключение
В статье было приведено описание, способ расчета баланса мощностей для постоянного и переменного тока. Для электротехники данный баланс очень важен, ведь с помощью него можно выполнять различные расчеты.
Видео по теме
Баланс мощностей
Содержание:
Баланс мощностей
Для любой электрической цепи суммарная мощность 
, развиваемая источниками электрической энергии (источниками тока и ЭДС), равна суммарной мощности 
, расходуемой потребителями (резисторами):
Мощность, рассеиваемая резистором, 
, мощность источника ЭДС 
, мощность источника тока 
.
Мощности, рассеиваемые резисторами, всегда положительные, в то время как мощности источников электрической энергии, в зависимости от соотношения направления падений напряжения и тока в них, могут иметь любой знак. Мощность положительна, когда направление тока через источник тока противоположно падению напряжения на нем. Он питает электрическую цепь. В противном случае источник питания является отрицательным, и вы являетесь потребителем электрической энергии. Следует заметить, что направление падения напряжения всегда противоположно направлению ЭДС, поэтому для источника ЭДС условием положительной мощности является совпадение направлений ЭДС и тока.
Пример расчёта разветвлённой цепи постоянного тока
Рассмотрим решение задачи для цепи, представленной на рис. 1.6, описанными выше методами расчёта.
Дано 
1) все неизвестные токи, используя законы Кирхгофа; показать, что баланс мощностей имеет место;
1) Применение законов Кирхгофа. Баланс мощностей.
Возможно вам будут полезны данные страницы:
Выберем положительные направления токов и обозначим их стрелками. Выберем и обозначим стрелками направления обхода трёх независимых контуров: 
Составим систему уравнений по законам Кирхгофа
для узла а 
;
для узла b 
для узла с 
или 
;
для контура 
,
для контура 
для контура 
Полученные уравнения после подстановки в них числовых значений будут иметь следующий вид:
Решение данной системы: 
Баланс мощностей для рассматриваемой цепи
Получено тождество 252 Вт = 252 Вт.
Примечание: падение напряжения на источнике тока 
определено по второму закону Кирхгофа для контура, содержащего 
и 
, как 
Баланс мощностей
В левой части равенства слагаемое берется со знаком «+» если Е и I совпадают по направлению и со знаком 
если не совпадают.
Если направления ЭДС и тока I в источнике противоположны, то физически это означает, что данный источник работает в режиме потребителя.
На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).
Услуги:
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Что такое баланс мощностей в цепи переменного тока
Баланс мощностей
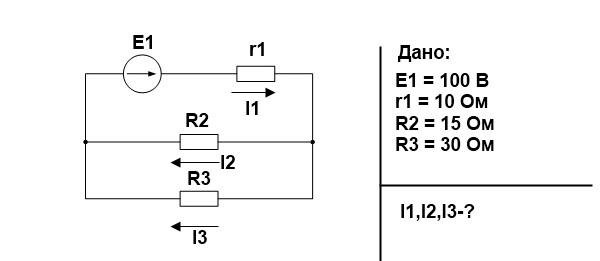
При решений электротехнических задач, часто нужно проверить правильность найденных значений. Для этого в науке ТОЭ, существует так называемый баланс мощностей.
Баланс мощностей – это выражение закона сохранения энергии, в электрической цепи. Определение баланса мощностей звучит так: сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками. То есть если источник ЭДС в цепи отдает 100 Вт, то приемники в этой цепи потребляют ровно такую же мощность.
Проверим это соотношение на простом примере.
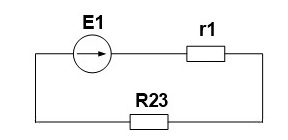
Для начала свернем схему и найдем эквивалентное сопротивление. R2 и R3 соединены параллельно.
Найдем по закону Ома ток источника и напряжение на R23, учитывая, что r1 и R23 соединены последовательно, следовательно, сила тока одинаковая.
Теперь проверим правильность с помощью баланса мощностей.
Небольшое различие в значениях связано с округлениями в ходе расчета.
С помощью баланса мощностей, можно проверить не только простую цепь, но и сложную. Давайте проверим сложную цепь из статьи метод контурных токов.
Как видите независимо от сложности цепи, баланс сошелся, и должен сойтись в любой цепи!
Как заполнить строки
Рассмотрим, какие счета и каким образом используются при формировании баланса, в соответствии с Планом счетов БУ (приказ Минфина № 94н).
Актив
Так заполняется 1-й раздел актива баланса «Внеоборотные активы»:
Порядок заполнения 2-й раздела актива баланса «Оборотные активы»:
Пассив
Так заполняется 3-й раздел пассива баланса «Капитал и резервы»:
Порядок заполнения 4-го раздела пассива баланса «Долгосрочные обязательства»:
Баланс мощностей в цепях переменного тока
Тогда полная комплексная мощность данного участка равна:
где – сдвиг фаз между напряжением и током.
, [Вт] – активная мощность участка,
, [ВАр] – реактивная мощность участка.
При выполнении условия баланса мощностей активная и реактивная мощности источников питания должны равняться потребляемым активной и реактивной мощностям.
Мощности источника Э.Д.С. определяем по формуле:
где – сопряжённый комплекс тока в ветви с источником Э.Д.С.
Мощность источника тока:
где – напряжение на зажимах источника тока;
– сопряжённый ток источника тока.
Мощность источника Э.Д.С. входит в выражение баланса со знаком «+», если направление Э.Д.С. источника и тока в этой ветви совпадают; если направления Э.Д.С. источника и тока не совпадают, то мощность источника Э.Д.С. отрицательная.
Мощность источника тока входит в выражение баланса со знаком «+», если ток источника и напряжения на его зажимах направлены навстречу друг другу. При совпадении направлений тока источника и напряжения мощность источника отрицательная.
Активная и реактивная мощности потребителей равны соответственно:
где – модуль действующего значения тока i–ой ветви.
где – эквивалентное реактивное сопротивление i–ой ветви.
При выполнении условия баланса мощностей:
Примеры расчёта цепей однофазного синусоидального тока
Пример 6.1
Решение
Для расчёта будем использовать метод контурных токов.
Выражаем ток из предыдущего уравнения:
Ток во второй ветви определим как алгебраическую сумму контурных токов, проходящих через данную ветвь:
Полная мощность приёмников определяется по формуле:
Активную мощность приёмников в данной схеме определим по следующей формуле:
Реактивную мощность приёмников определяем по формуле:
Полная мощность, выделяемая в систему источниками, определяется по формуле:
Выполнение баланса мощностей подтверждает правильность решения задачи.
Пример 6.2
Решение
Записываем функцию времени в виде показательной формы комплексного числа:
Определяем входное сопротивление схемы относительно зажимов источника напряжения:
Мгновенное значение тока имеет вид:
Пример 6.3
Решение
Графоаналитический метод расчёта – это совокупность графического метода и метода пропорционального пересчёта. Метод основан на линейной зависимости между токами и напряжениями. Поэтому векторная диаграмма напряжений и токов, рассчитанная и построенная для одного значения, питающего цепь напряжения, сохранит свой вид при изменении величины этого напряжения. На диаграмме изменятся лишь масштабы напряжений и токов.
Токи и напряжения, определённые с помощью диаграммы, будем обозначать одним штрихом.
Определяем по законуОма для действующих значений напряжения на участках « » и « » цепи.
Сумма векторов и определяет вектор напряжения на участке «c
Метод расчета по законам Ома и Кирхгофа
До изучения технологий вычислений необходимо уточнить особенности типовых элементов при подключении к разным источникам питания. При постоянном токе сопротивлением индуктивности можно пренебречь. Конденсатор эквивалентен разрыву цепи. Также следует учитывать следующие различия разных видов соединений резисторов:
Закон Ома для участка цепи
Типовая аккумуляторная батарея легкового автомобиля вырабатывает напряжение U = 12 V. Бортовой или внешний амперметр покажет соответствующее значение при измерении. Соединение клемм проводом недопустимо, так как это провоцирует короткое замыкание. Если жила тонкая (
К сведению. Результат показанного расчета пригодится для поиска подходящего резистора. Следует делать запас в сторону увеличения. По стандарту серийных изделий подойдет элемент с паспортной номинальной мощностью 5 Вт.
Общее понятие
Электрическое напряжение определяется как отношение работы поля по переброске пробного заряда из одной заданной точки в другую к размеру потенциала. При дислокации единичного резерва выполняется работа, которая равняется напряжению на искомом участке. Общая мощность получают умножением работы электрического поля для единичного заряда на число потенциалов за определенную единицу времени.
В переменной электрической цепи выделяется 3 вида мощности:
В цепи переменного электричества формула для расчета постоянного тока применяется только для вычисления мгновенной мощности. Этот показатель претерпевает изменения во времени и почти не имеет практического смысла для всех остальных расчетов. Среднезначимый показатель мощности требует временной интеграции. Мгновенная мощность объединяется в течение определенного промежутка для расчета величины в магистрали с периодическим изменением силы переменного потока и синусоидального напряжения.
Коэффициент скорости преобразования
Мощностной коэффициент является показателем потребления тока при присутствии реактивного компонента и искажающей нагрузки. Значение коэффициента отличается от понятия косинуса сдвигаемого угла. Второе понятие характеризуется смещением протекающего переменного тока, напряжения и используется только при синусоидальном токе и силе равного значения.
Коэффициент равняется отношению расходуемой нагрузки к ее полному значению. При этом работа совершается за счет активного вида преобразования. При синусоидальном токе и вольтаже полная нагрузка находится в виде суммы реактивной и активной форм. Активная нагрузка приравнивается к усредненному произведению силы тока и напряжения и не может быть выше произведения аналогичных среднеквадратических размерностей. Мощностной коэффициент показывается в диапазоне от 0 до 1 или ставится в процентах от 0 до 100.
Что нужно знать на начальном этапе
Бухгалтерская отчетность должна составляться с использованием актуальных форм документов. Приказ Минфина № 66н от 02/07/10 г. в ред. от 19/04/19 г. содержит такой бланк баланса. Обратим внимание, что с 2021 года приказ начинает действовать полностью, тогда как ранее организация была вправе не применять его.
Стандартная полная форма баланса содержит статьи, которые могут потребоваться бухгалтеру для заполнения формы. Баланс составляется с учетом специфики деятельности фирмы, наличия или отсутствия конкретного вида данных. Соответственно, не все строки могут быть заполнены. Кроме того, строки при необходимости можно детализировать, добавлять. Об этом сказано в ПБУ 4/99 (п. 11), приказе № 66н п. 3.
В новой форме есть графа «Пояснения», давать комментарии можно постатейно, рядом с соответствующими цифрами. Графа может использоваться при внесении нехарактерных для деятельности компании данных, добавлении строк и других отклонениях от стандарта. Дополнительные пояснения могут быть важны и при внесении сведений, имеющих существенный «вес» в общей сумме актива или пассива, в целях расшифровки стратегически значимых балансовых статей.
Внимание! Баланс сдается в ФНС, копия пояснительной записки к нему – в ФСС (кроме представителей малого бизнеса). В Росстат бухотчетность организации не сдают.
Общие правила составления баланса прописаны в ПБУ 4/99. Отметим наиболее важные:
Кроме того, перед составлением баланса необходимо провести инвентаризацию (ПБУ по ведению бухучета и отчетности в РФ, утв. пр. Минфина № 34н от 29/07/98 г., п. 27).Инвентаризируются активы: складские остатки, основные средства, готовая продукция и пр. Также инвентаризируются и обязательства, начиная с расчетов, «кредиторки», и далее кредиты, резервы.
Для составления баланса в основном используется регистр БУ оборотно-сальдовая ведомость по счетам. Данные ведомости должны быть предварительно тщательно проверены и сведены с использованием метода двойной записи. Балансовые показатели формируются по конечным остаткам.Дополнительно могут учитываться аналитические данные, данные листков-расшифровок.
Практическое применение и коррекция
Если к розетке с синусоидальным напряжением 50 Гц и 230 В подсоединить нагрузку с опережением или отставанием тока от напряжения на какую-то угловую величину, то на активной внутренней катушке будет создаваться увеличенная мощность. Это значит, что при работе в таких условиях выделяется много тепла, и электростанция отводит его в увеличенном количестве, по сравнению с применением активной нагрузки.
Коэффициенты полезного действия и мощности отличаются друг от друга. Мощностной показатель не влияет на потребление приемника, подключенного к сети, но изменяет энергетические потери в подводных проводах и местах выработки энергии или ее преобразования. В доме электросчетчик не реагирует на проявление мощности, так как оплачивается только та энергия, за счет которой работают приборы.
КПД влияет на потребляемую активную нагрузку. Например, энергосберегающая лампа потребляет в полтора раза больше электричества, чем аналогичный прибор накаливания. Это говорит о высоком коэффициенте полезного действия у первой лампы. Но показатель нагрузки может быть низким и высоким в обоих вариантах.
Коррекция заключается в приведении потребления прибора с низким мощностным коэффициентом к стандартным показателям при питании от силовой цепи переменного тока. Технически это осуществляется применением действенной схемы на входном устройстве, которая помогает равномерно использовать фазную мощность и исключает перегрузку нулевого провода. При этом снижаются всплески потребительского тока на верхушке синусоиды питающего вольтажа.
Реактивная нагрузка корректируется при включении в магистраль элемента с обратным действием. Например, в двигателе переменного тока для компенсации действия ставится конденсатор параллельно питающей линии. Применяется система активного или пассивного корректора при изменении используемого тока во время колебательного периода подпитывающего напряжения для преобразования коэффициента. Простым примером является последовательное подключение дросселя. При этом конечные приборы потребляют ток непропорционально гармоничным искажениям. Катушка сглаживает волновые импульсы.
Баланс мощностей с источником тока
При решений электротехнических задач, часто нужно проверить правильность найденных значений. Для этого в науке ТОЭ, существует так называемый баланс мощностей.
Баланс мощностей – это выражение закона сохранения энергии, в электрической цепи. Определение баланса мощностей звучит так: сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками. То есть если источник ЭДС в цепи отдает 100 Вт, то приемники в этой цепи потребляют ровно такую же мощность.
Или 
Проверим это соотношение на простом примере.
Для начала свернем схему и найдем эквивалентное сопротивление. R2 и R3 соединены параллельно.
Найдем по закону Ома ток источника и напряжение на R23, учитывая, что r1 и R23 соединены последовательно, следовательно, сила тока одинаковая.
Теперь проверим правильность с помощью баланса мощностей.
Небольшое различие в значениях связано с округлениями в ходе расчета.
С помощью баланса мощностей, можно проверить не только простую цепь, но и сложную. Давайте проверим сложную цепь из статьи метод контурных токов.
Как видите независимо от сложности цепи, баланс сошелся, и должен сойтись в любой цепи!
Баланс мощностей в электрической цепи означает, что мощность, которую выделяют все источники энергии, равна мощности, которую потребляют в этой же цепи все приемники энергии:
, (2.69)
где 
– мощность i-го источника ЭДС или тока, Вт; 
– мощность, выделяемая в j-м сопротивлении, Вт.
Очевидно, что баланс мощностей следует из закона сохранения энергии.
Запишем для анализируемой цепи рис. 2.15 сумму мощностей, выделяемых всеми источниками энергии. При этом мощности, выделяемые источниками ЭДС и тока, будем считать положительными, если ток в ветви, где установлен источник ЭДС или тока, совпадает с направлением тока внутри источника (со стрелкой в обозначении источника ЭДС или тока), и отрицательными, если направление тока в ветви противоположно направлению тока в источнике. Тогда, составив соответствующее уравнение для вычисления суммарной мощности, отдаваемой источниками ЭДС и тока в анализируемую цепь и подставив в него численные значения, получим суммарную мощность источников:
[Вт]. (2.70)
при этом токи ветвей должны подставляться в уравнение (2.70) со своим знаком, который получился при их расчете.
Суммарная мощность, рассеиваемая в цепи сопротивлениями (приемниками энергии), для той же цепи рис. 2.15, может быть найдена так:
[Вт]. (2.71)
В результате расчета (2.70) – выделяемая источниками мощность, и (2.71) – потребляемая сопротивлениями мощность в цепи – должны быть одинаковы.
Потенциальная диаграмма электрической цепи
Постоянного тока
Потенциальная диаграмма контура электрической цепи постоянного тока – это графическое изображение второго закона Кирхгофа, в котором вместо падений напряжений записаны потенциалы узлов электрической цепи. Она показывает суммарное значение потенциала и суммарное сопротивление в данной точке цепи того контура, для которого построена диаграмма, считая от опорного узла, потенциал которого принят за нулевой. Иными словами, потенциальная диаграмма показывает распределение потенциалов и сопротивлений в том контуре цепи, для которого она построена.
Графически эта диаграмма представляет собой ломаную линию, изображенную в декартовой системе координат, горизонтальной осью которой (осью абсцисс) является ось сопротивлений 
, а вертикальной осью (осью ординат) – ось потенциалов 
.
Процесс построения потенциальной диаграммы электрической цепи рассмотрим для той же, что и ранее, электрической цепи, показанной на рис. 2.3, и модифицированной для удобства построения потенциальной диаграммы так, как показано на рис. 2.15.
Поскольку для построения потенциальной диаграммы требуется знание численных значений токов ветвей и сопротивлений ветвей, приведем эти численные значения для цепи рис. 2.15 при условии, что исходные данные для расчета этой цепи таковы: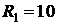 
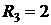
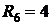
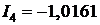
Ом, 
Ом, 
Ом, 
Ом, 
Ом, 
Ом; величины источников ЭДС: 
В, 
В; величины источников тока: 
А, 
А. Значения токов 
в ветвях цепи, рассчитанные прямым применением законов Кирхгофа (сам расчет здесь не приводится), таковы: 
[А]; 
[А]; 
[А]; 
[А]; 
[А]; 
[А].
Построение потенциальной диаграммы начнем с выбора контура, для которого эта диаграмма будет составляться. На наш взгляд, наиболее информативно будет построить потенциальную диаграмму для контура d-b-m-a-c-s-d, так как в этом контуре содержатся все источники ЭДС и источники тока анализируемой цепи и при таком обходе на потенциальной диаграмме будут показаны потенциалы всех узлов анализируемой схемы. Далее произведем выбор опорного узла, потенциал которого примем за ноль. Есть смысл взять за опорный узел d, как и ранее при расчетах анализируемой цепи. Потенциал этого узла положим равным нулю, как и ранее (2.44).
Определим численные значения потенциалов узлов и точек анализируемой схемы, находящихся на пути обхода выбранного нами контура d-b-m-a-c-s-d. Поскольку потенциал узла d равен нулю (2.44), то потенциал 
узла b определится так:
[В]. (2.72)
Знак «плюс» при произведении 
означает, что потенциал узла b повышается при переходе от узла d анализируемой схемы к узлу b (см. полярность падения напряжения на сопротивлении 
от тока 
на схеме рис. 2.15).
Следующим определим потенциал 
точки m анализируемой схемы:
[В]. (2.73)
Знаки при произведениях 
и 
соответствуют полярностям, показанным на схеме рис. 2.15.
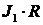
Следующим за точкой m анализируемой схемы идет узел a. Его потенциал 
равен:
[В]. (2.74)
Рис. 2.15. Эквивалентная схема анализируемой электрической цепи для построения потенциальной диаграммы
Далее определим потенциал 
узла c, значение которого составит:
[В]. (2.75)
Потенциал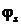 
точки s, следующей за узлом c по выбранному нами обходу, равен:
[В]. (2.76)
Обойдя таким образом весь контур d-b-m-a-c-s-d, мы возвращаемся в узел d. При этом потенциал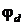 
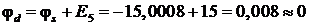
узла d должен стать равным нулю. В самом деле, так оно и происходит, так как при подходе из узла c к узлу d, потенциал последнего станет равен:
[В]. (2.77)
После расчета численных значений потенциалов для контура d-b-m-a-c-s-d можно построить саму потенциальную диаграмму. Эта диаграмма показана на рис. 2.16.
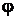
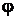
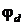
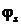
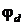
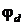
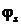
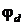
Техника построения потенциальной диаграммы такова. На осях декартовой системы координат откладывают значения потенциалов и сопротивлений для контура цепи (схемы), который был ранее выбран для построения потенциальной диаграммы. В нашем примере, рис. 2.15, это контур d-b-m-a-c-s-d. Значения заранее рассчитанных величин потенциалов для каждой из точек этого контура откладывают на вертикальной оси (оси ординат) в положительную или отрицательную область значений, в зависимости от знака потенциала, полученного ранее при расчете. В нашем примере это будут потенциалы , , , , , и вновь точек d-b-m-a-c-s-d, соответственно. Порядок следования значений потенциалов в потенциальной диаграмме соответствует их порядку при расчете значений потенциалов. В анализируемой нами цепи рис. 2.15, этот порядок , , , , , , соответствует обходу контура d-b-m-a-c-s-d. Значения сопротивлений откладываются по горизонтальной оси (оси абсцисс) декартовой системы координат. За нулевое (исходное) значение сопротивления в потенциальной диаграмме принимается значение в опорном узле; в нашем примере рис. 2.15 это значение сопротивления в узле d. Далее, по мере обхода контура цепи, который выбран для построения потенциальной диаграммы (в нашем примере это контур d-b-m-a-c-s-d), значения сопротивлений в каждой последующей точке прибавляются к значениям сопротивлений в предыдущей точке.
Таким образом, сопротивление в каждой точке потенциальной диаграммы контура оказывается суммарным для этой точки, начиная с опорного узла, где значение сопротивления принято за ноль. Если при переходе из одной точки контура в другую сопротивления в схеме цепи нет, то к предыдущему значению сопротивления прибавляется ноль (это имеет место при прохождении источника ЭДС с нулевым внутренним сопротивлением).
Рис. 2.8.2 Потенциальная диаграмма контура d-b-m-a-c-s-d исследуемой цепи
В нашем примере значения сопротивлений в точках потенциальной диаграммы контура d-b-m-a-c-s-d составят:
[Ом]. (2.78)
Таким образом, при построении потенциальной диаграммы контура электрической цепи по вертикальной оси декартовой системы координат откладывают потенциалы узлов по мере их упоминания при обходе контура, а по горизонтальной оси – нарастающим итогом сопротивления также по мере их упоминания при таком обходе. Используют потенциальную диаграмму цепи для наглядного визуального представления распределения потенциалов и соответствующих им сопротивлений по тому или иному контуру электрической цепи.
Библиографический список
1. Основы теории цепей. Методические указания и контрольные задания для студентов радиотехнического факультета спец. 0701 “Радиотехника”.-Сост. Ю.А.Мантейфельд, А.Д.Суслов. М.: МИРЭА.-1980.-48 с.
2. Основы теории цепей. Методические указания по выполнению расчетно-графических заданий №1-2 для студентов радиотехнического факультета. Сост. В.И.Вепринцев. Красноярск: Изд-во КГТУ, 2000. 64 с.
3. Шебес, М.Р., Каблукова, М.В. Задачник по теории линейных электрических цепей: Учеб. пособ. для электротехнич., радиотехнич. Спец. вузов.-4-е изд. перераб. и доп.-М.: Высш. шк., 1990.-544 с.: ил.
4. Основы теории цепей: учебник для вузов / Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. – 5-е изд., перераб. – М.: Энергоатомиздат, 1989. – 528 с.
5. Теория линейных электрических цепей: учебник для вузов / Б.П.Афанасьев, О.Е.Гольдин, И.Г.Кляцкин, Г.Я.Пинес. – М.: Высш. шк., 1973. – 592 с.
Оглавление
1. ЗАДАНИЕ И ВЫБОР ВАРИАНТА ДЛЯ ЕГО ВЫПОЛНЕНИЯ.. 4
2. РАСЧЕТ ВЕЛИЧИН ТОКОВ НЕПОСРЕДСТВЕННЫМ ПРИМЕНЕНИЕМ ЗАКОНОВ КИРХГОФА, МЕТОДАМИ КОНТУРНЫХ ТОКОВ, УЗЛОВЫХ ПОТЕНЦИАЛОВ И МЕТОДОМ ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА.. 9
2.2. Анализ (расчет) сложных электрических цепей. 19
методом контурных токов. 19
2.6.3 Анализ (расчет) сложных электрических цепей. 25
методом узловых потенциалов. 25
2.6.4 Анализ (расчет) сложных электрических цепей. 31
методом эквивалентного генератора. 31
2.5. Баланс мощностей в электрической цепи постоянного тока. 40
2.6 Потенциальная диаграмма электрической цепи. 41
постоянного тока. 41
Библиографический список. 47
Дата добавления: 2018-02-15 ; просмотров: 2258 ; ЗАКАЗАТЬ РАБОТУ
Баланс мощностей является следствием закона сохранения энергии — суммарная мощность вырабатываемая (генерируемая) источниками электрической энергии равна сумме мощностей потребляемой в цепи.
Источники E1 и E2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадают (если ЭДС и ток в ветвях направлены в противоположную сторону, то источник ЭДС потребляет энергию и его записывают со знаком минус). Баланс мощностей для заданной цепи запишется так:
С учетом погрешности расчетов баланс мощностей получился.
Похожие статьи:
7 thoughts on “Баланс мощностей в цепи постоянного тока”
Блин все ошибки найдут, в условии должно быть Е1 = 20, Е2 = 30.
P.S. Сейчас исправлю, спасибо за внимательность
Какова допустимая погрешность?? У меня выходит 0,561
По идее баланс мощности должен равняться нулю, но так как мы округляем некоторые значения при расчете — возникает погрешность, которая может составлять примерно 0,1 — 5% от потребляемой мощности.
Про знаки ЭДС сказано про знаки мощностей приёмников — нет.