Для чего логарифмическая шкала
Reveal the Data
Выбор типа шкал для графика, всегда казалось мне интуитивно понятной задачей. Однако, когда мне нужно было объяснить, чем они отличаются, то я не смог привести понятных аргументов. В интернете хорошей информации мне не попалось. Поэтому решил разобраться, откуда растут ноги у разных видов шкал и как их следует применять. Я решил рассмотреть три самых распространенных вида шкал — равномерную, логарифмическую и степенную.
Равномерная шкала
Самый распространенный и привычный вид шкал. Также их называют арифметическими или линейными шкалами. На такой шкале значения равноудалены друг друг от друга.
Например значения 100 и 200, и 200 и 300 отстают друг от друга на одно и тоже расстояние.
Например, на этом графике по оси Y — равномерная шкала с шагом в 20 лет средней продолжительности жизни, а по оси X — равномерная шкала с шагом 10 календарных лет.
Логарифмическая шкала
Этот вид шкал тоже используется достаточно часто, особенно когда речь идёт о научных исследованиях. Она используется для отображения широко диапазона величин, когда значения, которые попадают на график отличаются на много порядков. То есть когда мы хотим одновременно видеть и значения 0.1, 0.2 и значения 100, 200 на одном графике. Зачастую это связанно с физикой процесса. Так, например, в музыке ноты, различающиеся по частоте в два раза это ноты на октаву выше (Ля и Ля следующей октавы). Чтобы показать частоты двух нот будет удобно использовать логарифмическую шкалу.
Но бывает, что в наборе данных просто содержаться большой разброс данных. Например, как на этом графике из Beautiful Evidence Тафти, где он использует логарифмические шкалы для сравнения массы тела и мозга различных существ. Так как бывают и крошечные рыбки и огромные киты, то на таком графике удобно использовать логарифмические шкалы.
Чаще всего используются логарифмические шкалы с основанием 10. Это значит, что одинаковые расстояние на графике откладываются между значениями отличающимися на один порядок. Но бывают логарифмические шкалы с другими основаниями. Например 2.
Степенная шкала
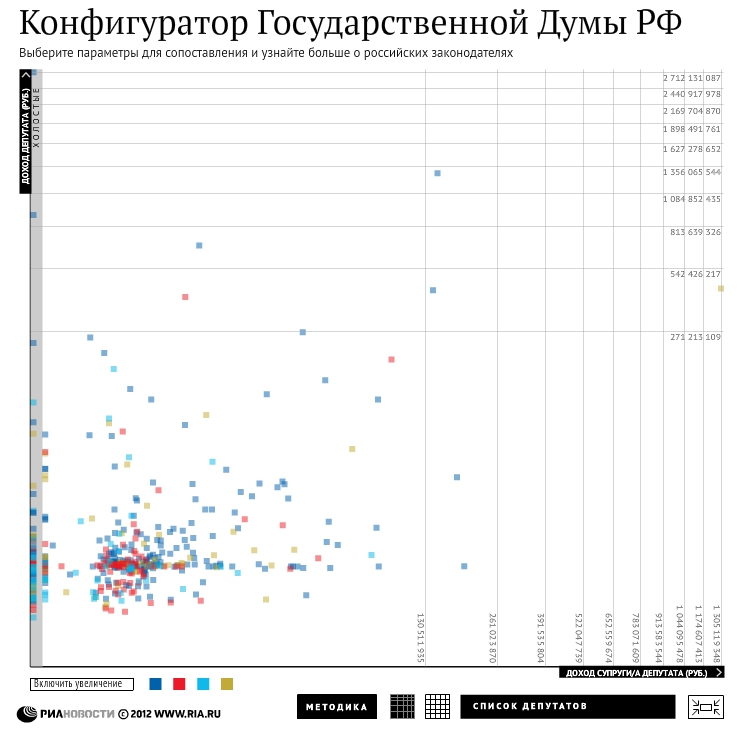
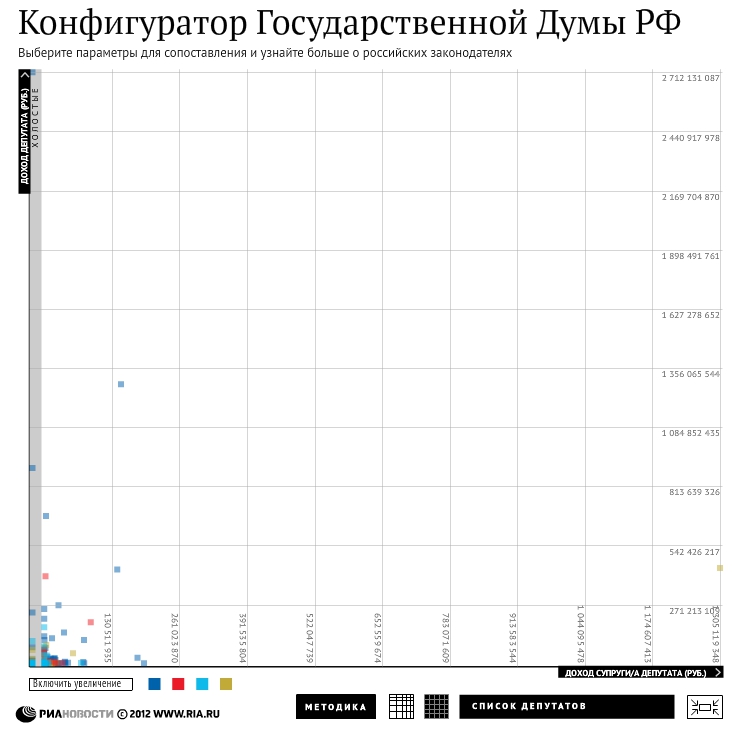
Это менее известный тип шкал. Он отличается от остальных тем, что расстояние между рисками, соответствует числам возведенным в степень. То есть получается, что расстояние между соседними рисками постоянно растёт или уменьшается. Такие шкалы удобны, когда мы хотим показать на одном графике более детально какую-то группу значений, но при это не хотим потерять из вида, значения которые, сильно отличаются от этой группы. Чем-то это похоже на логарифмическую шкалу, но здесь идёт акцент не на всем промежутке, а только на отдельной его части. Это хорошо видно на примере РИА новости, где они использовали степенные шкалы, чтобы сгладить выбросы по доходам отдельных депутатов.
Со степенной шкалой
С равномерной шкалой
То есть степенные шкалы используются когда данные смещены в ту или иную сторону.
Сравнение шкал
Чтобы удобно сравнить и понять как использовать ту или иную шкалу, я сделал небольшой инструмент. На нём можно выбрать разные наборы данных и понять, как они выглядят на разных шкалах.
Почему я пользуюсь логарифмической шкалой при просмотре графика цены акций?
Вводная заметка о пользе логарифмов.
Думаю, все вы понимаете, что конкретная цена акции не имеет никакого значения. Главное, чтобы её цена была не выше той суммы, которую инвестор хочет потратить. Например, акция BRK.A стоит порядка 420к$, что явно переходит все границы разумного. Но в остальном, если вы хотите купить акции какой-то компании на условные сотню баксов, то вам, в принципе, всё равно, будет ли это десять акций по десять долларов или сотня акций по доллару.
Значение имеет то, на сколько процентов цена изменилась. То, что какая-то акция поднялась на доллар — ничего вам не говорит, если вы не знаете, какая у неё была прошлая стоимость, потому что 1+1 и 10+1 — это совершенно разные вещи. С другой стороны, если акция поднялась на 25%, то вам совершенно не обязательно знать, сколько она стоила раньше — вы и так получили всю нужную информацию.
Допустим теперь, что вы анализируете поведение акции за большой временной период — несколько лет или даже десятилетий. Если компания развивалась всё это время, то цены сейчас намного выше цен более раннего периода. Например, акция TSLA совсем недавно стоила 900$, а несколько лет назад она стоила всего лишь 50$:
Если мы посмотрим на график выше, то колебания цены мы увидим только начиная с 2020 года. А начиная с 2014 года и до 2020 идет чуть ли не прямая линия, как будто цена акции все эти годы стояла на месте. Почему так? Потому что на фоне колебаний цены между 900$ и 550$, колебания между 30$ и 70$ совершенно не видны. А ведь в процентах второй случай куда как значимей.
А еще падение с 180$ до 70$ в начале 2020 года в процентах примерно в полтора раза сильнее падения с 900$ до 550$ в начале 2021 года, но на графике более позднее событие выглядит куда как страшнее более раннего.
Получается, что такой график не просто теряет часть информации, но и вводит нас в заблуждение.
Тут на помощь приходит логарифмическая шкала. Преимущество такой шкалы в её нелинейности. Я не буду объяснять, что такое логарифм — это вы можете сами в Википедии почитать. Да и, как известно, каждая дополнительная формула в статье уменьшает количество её читателей в два раза 🙂
На графике выше — та же акция, с тем же временным промежутком, но только в логарифмическом представлении. Сравните с прошлым, линейным графиком, и убедитесь, насколько понятней выглядит поведение цены за весь период времени, а не только за последний год.
Вообще говоря, кванты и алготрейдеры вовсю используют логарифмы, чтобы избавиться от «шума» в данных. Если я когда-нибудь найду достаточно времени, чтобы обучать алготрейдингу, то мы еще вернемся к этой теме.
Самостоятельно поиграться с логарифмическим представлением цен можно, к примеру, на TradingView, в настройках графика.
Если то, что я пишу, вам кажется интересным — подписывайтесь на мой телеграм-канал, чтобы своевременно получать уведомления о новых постах:
Поскриптум: я не инвестиционный консультант и никогда им не был. Ничто из вышенаписанного не следует рассматривать как инвестиционную рекомендацию.
Логарифмическая шкала
Отметки на линейках расположены в логарифмической шкале для умножения или деления чисел путем добавления или вычитания длин на шкалах.
Ниже приведены примеры обычно используемых логарифмических шкал, где большее количество приводит к более высокому значению:
Ниже приведены примеры обычно используемых логарифмических шкал, где большее количество приводит к более низкому (или отрицательному) значению:
Некоторые из наших чувств действуют логарифмически ( закон Вебера-Фехнера ), что делает логарифмические шкалы для этих входных величин особенно подходящими. В частности, наш слух воспринимает равные отношения частот как равные различия в высоте тона. Кроме того, исследования маленьких детей в изолированном племени показали, что логарифмические шкалы являются наиболее естественным отображением чисел в некоторых культурах. [1]
На верхнем правом графике используется шкала log-10 только для оси X, а на нижнем правом графике используется шкала log-10 как для оси X, так и для оси Y.
Представление данных в логарифмической шкале может быть полезно, когда данные:
Линейка скольжения имеет логарифмическую шкалу, а номограммы часто используют логарифмическую шкалу. Среднее геометрическое двух чисел на полпути между числами. До появления компьютерной графики логарифмическая миллиметровка была широко используемым научным инструментом.
Лог – логарифмические графики
Полулогарифмические графики
Если только ордината или абсцисса масштабируются логарифмически, график называется полулогарифмическим графиком.
Примеры
Единицы информации
Единицы измерения уровня или разницы уровней
Единицы частотного интервала
Таблица примеров
| Ед. изм | Основание логарифма | Базовое количество | Интерпретация |
|---|---|---|---|
| немного | 2 | количество возможных сообщений | количество информации |
| байт | 2 8 = 256 | количество возможных сообщений | количество информации |
| децибел | 10 (1/10) ≈ 1,259 | любое количество мощности (например, звуковая мощность ) | уровень звуковой мощности (например) |
| децибел | 10 (1/20) ≈ 1,122 | любая основная величина мощности (например, звуковое давление ) | уровень звукового давления (например) |
| полутон | 2 (1/12) ≈ 1,059 | Частота от звука | интервал подачи |
Мотивация
Мотивация, лежащая в основе концепции логарифмических единиц, заключается в том, что определение величины в логарифмической шкале в терминах логарифма с определенным основанием равносильно совершению (совершенно произвольного) выбора единицы измерения для этой величины, соответствующей конкретной (и в равной степени произвольно) выбранное основание логарифма. Из-за идентичности
ЛОГАРИФМИЧЕСКАЯ ШКАЛА
Полезное
Смотреть что такое «ЛОГАРИФМИЧЕСКАЯ ШКАЛА» в других словарях:
логарифмическая шкала — Шкала, построенная на основе систем логарифмов. Примечание Для построения логарифмических шкал обычно используются системы десятичных или натуральных логарифмов, а также система логарифмов с основанием два. [МИ 2365 96] Тематики метрология,… … Справочник технического переводчика
логарифмическая шкала — 2.2.7 логарифмическая шкала : Шкала измерений, получаемая логарифмическим преобразованием измеряемой величины. Источник: РМГ 83 2007: Государственная система обеспечения единства измерений. Шкалы измерений. Термины и определения … Словарь-справочник терминов нормативно-технической документации
Логарифмическая шкала — На шкале в логарифмическом масштабе длина отрезка шкалы пропорциональна логарифму отношения величин отмеченных на концах этого отрезка (в то время как на шкале в линейном масштабе длина отрезка пропорциональна разности величин на его концах).… … Википедия
логарифмическая шкала — logaritminė skalė statusas T sritis automatika atitikmenys: angl. logarithmic scale vok. logarithmische Skala, f rus. логарифмическая шкала, f pranc. échelle logarithmique, f … Automatikos terminų žodynas
логарифмическая шкала — logaritminė skalė statusas T sritis Standartizacija ir metrologija apibrėžtis Logaritminiu masteliu sudaryta skalė. atitikmenys: angl. logarithmic scale vok. logarithmische Skala, f rus. логарифмическая шкала, f pranc. échelle logarithmique, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
логарифмическая шкала — logaritminė skalė statusas T sritis fizika atitikmenys: angl. logarithmic scale vok. Logarithmenskala, f rus. логарифмическая шкала, f pranc. échelle logarithmique, f … Fizikos terminų žodynas
Логарифмическая шкала разностей — Логарифмическая шкала измерений, получаемая при логарифмическом преобразовании величины, описываемой шкалой отношений, или интервала в шкале разностей, т.е. шкала, определяемая зависимостью L = log (Х/Х0), где Х текущее, a X0 принятое по… … Словарь-справочник терминов нормативно-технической документации
логарифмическая шкала разностей — Логарифмическая шкала измерений, получаемая при логарифмическом преобразовании величины, описываемой шкалой отношений, или интервала в шкале разностей, т.е. шкала, определяемая зависимостью L = log (X/X0), где Х текущее, а Х0 принятое по… … Справочник технического переводчика
логарифмическая шкала для частот — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN logarithmic frequency scale … Справочник технического переводчика
Логарифмическая шкала времени — вид логарифмической шкалы, которая показывает наиболее значимые исторические события на одной странице в десяти строках в логарифическом масштабе.[источник не указан 448 дней] События далёкого прошлого имеют меньшее влияние на … Википедия
Для чего логарифмическая шкала
Основные свойства счетной линейки и в первую очередь правило пропорций вытекают из того, что шкалы счетной линейки являются логарифмическими.
Шкала называется логарифмической, если на ней нанесены логарифмы чисел, а отметками шкалы являются сами числа.
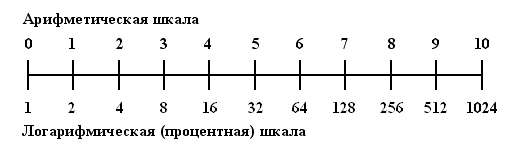
На рисунке представлена логарифмическая шкала х рядом с равномерной шкалой у, на которой нанесены десятичные логарифмы чисел х.
Логарифмическая шкала простирается неограниченно в обе стороны. Слева от точки х=1 находятся положительные числа, меньшие 1, десятичные логарифмы которых отрицательны. (Мы здесь и в дальнейшем будем употреблять термины «точка х» и «число х» как равносильные, подобно тому как это делается при работе с числовой осью.)
Основные шкалы А и В счетной линейки представляют собой только один отрезок [1, 10] логарифмической шкалы. Шкалы С и D представляют собой отрезок [1, 100] логарифмической шкалы, а шкала К — отрезок [1, 1000] той же шкалы.
Шкала L представляет собой равномерную шкалу, точки 0 и 1 которой находятся соответственно против чисел 1 и 10 шкалы В из сказанного выше, а также из рисунка ясно, что шкала L дает десятичные логарифмы чисел шкалы В.
1. Вывод правила пропорций (см. раздел «Правило пропорций»). Сначала найдем расстояние ρ [а, b] между двумя точками х = а и x = b (b > а) логарифмической шкалы. Воспользуемся для этого равномерностью шкалы у = lgx длина отрезка шкалы у, совпадающего с отрезком [а, b] шкалы х пропорциональна разности lgb — lga.
Обозначая коэффициент пропорциональности через λ, получим
В частности, расстояние любой точки х логарифмической шкалы от точки 1 пропорционально десятичному логарифму числа х
Коэффициент λ равен длине отрезка [1, 10] логарифмической шкалы (т. е. единице масштаба оси у), как видно из формулы
Возьмем теперь две одинаковые и параллельно расположенные логарифмические шкалы, которые мы обозначим через А и В. Сместим шкалу А относительно шкалы В и рассмотрим любые пары чисел а1 и b1 а2 и b2, которые окажутся друг против друга на этих шкалах (см. раздел «Правило пропорций»).
Это значит, что для рассматриваемых чисел имеет место пропорция
Эта пропорция равносильна пропорции
которая и выражает доказываемое правило:
При любом смещении шкал А и В все числа шкалы А пропорциональны расположенным против них числам шкалы В.
Отметим, что доказанное правило пропорций относится ко всей бесконечной логарифмической шкале. Если бы мы имели возможность построить такую шкалу на счетной линейке, то мы могли бы вести расчеты с числами без их предварительной нормализации и без переброски движка. Необходимость нормализации исходных данных и применяемые в расчетах переброски движка вызваны тем, что на основных шкалах счетной линейки имеется только один отрезок логарифмической шкалы.
2. Свойство «периодичности» логарифмической шкалы. Из правила пропорций вытекает, что если шкалу А сдвинуть относительно шкалы В вправо на длину отрезка [1, 10], то все числа шкалы В будут в 10 раз больше расположенных против них чисел шкалы А:
Наконец, свойство периодичности позволяет нанести логарифмическую шкалу на окружность, что вообще снимает вопрос о перебросках движка. Такие круговые логарифмические шкалы реализованы в конструкциях логарифмического диска «Спутник» (см. раздел «Решение пропорций») и описываемой в приложении 3 Круговой логарифмической линейки КЛ-1.
3. Постоянство относительной погрешности. Погрешность установки чисел на шкале определяется тем расстоянием, на которое по техническим правилам допускается смещение штрихов шкалы. Так как смещение штрихов, не превышающее допуска, может встретиться на любом участке шкалы, то для равномерной шкалы абсолютная погрешность установки чисел будет одна и та же на всем протяжении шкалы. Иначе обстоит дело на логарифмических шкалах. Здесь оказывается постоянной не абсолютная, а относительная погрешность установки чисел. Это означает следующее. Пусть при установке чисел а и b на логарифмической шкале их абсолютные погрешности Аа и Аb вызваны тем, что отметки а и b смещены на одно и то же расстояние. Тогда из равенства этих расстояний
как и в пункте 1, вытекает пропорция
что и выражает равенство относительных погрешностей установки чисел а и b.
По существующим техническим правилам смещение штрихов на обычных счетных линейках не должно превосходить 0,2 мм. Это значит, что предельное допустимое смещение любой отметки а составляет
Отсюда по формуле расстояний получаем
Для основных шкал А к В нормальной линейки коэффициент дающий длину отрезка [1, 10] шкалы, равен 250 мм, поэтому
а значит, относительная погрешность установки чисел на основных шкалах А и В нормальной счетной линейки составляет около 0,2%.
На шкалах С и D коэффициент К вдвое меньше (125 мм) и поэтому относительная погрешность установки чисел на этих шкалах вдвое больше (≈ 0,4%).
4. Построение шкал степенных функций. Рассмотрим сначала соответствие между шкалами В и С корпуса. Шкала В представляет собой отрезок [1, 10] логарифмической шкалы с масштабным коэффициентом λ1 = 250 мм. Шкала С представляет собой отрезок [1, 100] логарифмической шкалы с масштабным коэффициентом λ2 = λ1/2 = 125 мм причем 1 шкалы С находится против 1 шкалы В.
Поэтому если точка u шкалы С находится против точки х0 шкалы В, то из равенства расстояний
Вот почему шкала С является шкалой квадратов для шкалы В. Аналогично строится шкала кубов К с масштабным коэффициентом λ3 = λ1/3.
Шкала квадратов и шкала кубов являются простейшими шкалами степенной функции. Легко построить шкалу степенной функции u = х r при любом показателе r > 0. Для этого достаточно параллельно шкале В аргумента х поместить еще одну логарифмическую шкалу с масштабным коэффициентом
и установить число u = 1 этой шкалы против числа х = 1 шкалы В. Действительно, при этом для соответственных точек х и u по формуле расстояния имеем
Таким путем можно построить на счетной линейке шкалу функции х r не только при любом целом, но и при любом дробном и даже иррациональном значении r. На обычных линейках ограничиваются случаями целых значений r = 2 и r = 3.
На обычных линейках подобные шкалы встречаются только для случая г = — 1 (шкала обратных величин).