Для чего людям понадобились рациональные числа
Что такое рациональные числа
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы вновь поговорим о математических терминах.
И на этот раз расскажем все о РАЦИОНАЛЬНЫХ ЧИСЛАХ. Они обязательно входят в школьную программу, и дети начинают изучать их в 6 классе.
Само слово «рациональный» знакомо многим. И под ним подразумевается нечто «логичное» и «правильное». На деле так и есть.
Термин имеет латинские корни, и в переводе «ratio» означает «число», «расчет», «разум», «рассуждение» и «нумерация». Но есть и другие переводы – «дробь» и «деление».
РАЦИОНАЛЬНОЕ ЧИСЛО – любое число, которое можно показать в виде дроби a/b. Здесь а – целое число, а b – натуральное.
Стоит напомнить, что:
И если применить эти определения, то мы можем сказать, что:
РАЦИОНАЛЬНОЕ ЧИСЛО – это вообще все возможные числа, кроме бесконечных непериодических десятичных дробей. Среди них натуральные и целые числа, обыкновенные и конечные десятичные дроби, а также бесконечные периодические дроби.
История изучения рациональных чисел
Точно неизвестно, когда люди начали изучать дроби. Есть мнение, что много тысяч лет назад. И началось все с банального дележа. Например, кому-то нужно было разделить добычу, но на равные части это не получалось сделать. Зато получалось сколько-то целых, и сколько-то в довесок.
Скорее всего, дроби изучали и в Древнем Египте, и в Древней Греции. Тогдашние математики далеко продвинулись в науке. И трудно предположить, что эта тема осталась ими не изучена. Хотя, к сожалению, ни в одних трудах так и не было найдено конкретных указаний на рациональные числа.
А вот официально считается, что понятие десятичной дроби появилось в Европе в 1585 году. Этот математический термин в своих трудах увековечил голландский инженер и математик Симон Стевин.
До занятия наукой, он был обыкновенным купцом. И скорее всего, именно в торговых делах часто сталкивался с дробными числами. Что потом и описал в своей книге «Десятая».
В ней Стевин не только объяснял полезность десятичных дробей, но и всячески пропагандировал их использование. Например, в системе мер для точного определения величины чего-либо.
Разновидности рациональных чисел
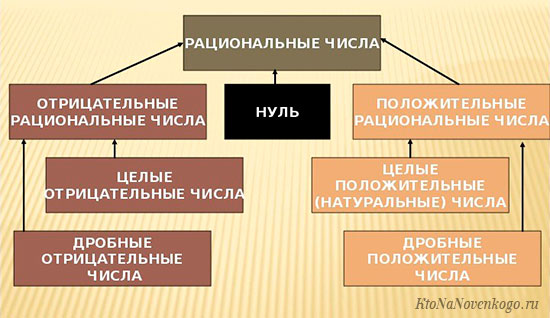
Мы уже написали, что под понятия рациональные числа подпадают практически все возможные варианты. Теперь рассмотрим более подробно существующие варианты:
Все числа, которые входят в понятие рациональных, называются МНОЖЕСТВОМ рациональных чисел. В математике его принято обозначать латинской буквой Q.
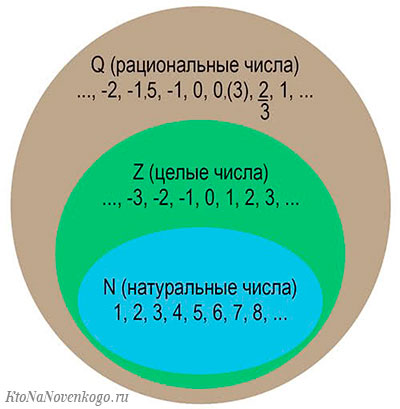
А графически это можно изобразить вот так:
Свойства рациональных чисел
Рациональные числа подчиняются всем главным законам математики:
Ради интереса можете попробовать подставить вместо букв любые числа и убедиться, что эти законы верны.
Вместо заключения
Раз есть в математике рациональные числа, значит, должны быть и им противоположные. Так и есть – они называются иррациональными. Это числа, которые нельзя записать в виде обычной дроби.
К таким числам относится математическая константа «пи». Многие знают, что она равна 3,14 и бесконечное количество знаков после запятой, причем их последовательность никогда не повторяется.
Также к иррациональным числам относится много корней. Это касается тех, у кого в результате не получается целого числа. Самый простой пример – корень из 2. Но это уже тема для другой статьи.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Такое понятие как «рациональные числа» прекрасно помню с университета, возможно даже со школьных времен, а вот какие это числа уже забылось. Кому-то пригодилось это знание вообще?
Рациональные числа: определения, примеры
Данная статья посвящена изучению темы «Рациональные числа». Ниже приведены определения рациональных чисел, даны примеры, рассказано о том, как определить, является ли число рациональным, или нет.
Рациональные числа. Определения
Прежде чем дать дефиницию рациональных чисел вспомним, какие еще есть множества чисел, и как они связаны между собой.
Натуральные числа, в совокупности с противоположными им и числом ноль образуют множество целых чисел. В свою очередь, совокупность целых дробных чисел образует множество рациональных чисел.
Определение 1. Рациональные числа
Таким образом, можно оставить ряд свойств рациональных чисел:
Приведенное выше определение рациональных чисел можно сформулировать более кратко. Еще раз ответим на вопрос, что такое рациональное число.
Определение 2. Рациональные числа
Можно показать, что данное определение равносильно предыдущему определению рациональных чисел. Чтобы сделать это, вспомним, что черта дроби равносильна знаку деления. С учетом правил и свойств деления целых чисел, можно записать следующие справедливые неравенства:
Таким образом, можно записать:
Приведем еще одну эквивалентную форму определения рациональных чисел.
Определение 3. Рациональные числа
Данное определение напрямую следует из самого первого определения этого пункта.
Подведем итог и сформулируем резюме по данному пункту:
Какое из чисел является рациональным?
Как мы уже выяснили, любое натуральное число, целое число, правильная и неправильная обыкновенная дробь, периодическая и конечная десятичная дробь являются рациональными числами. Вооружившись этими знаниями можно без труда определить, является ли какое-то число рациональным.
Однако на практике часто приходится иметь дело не с числами, а с числовыми выражениями, которые содержат корни, степени и логарифмы. В некоторых случаях ответ на вопрос «рационально ли число?» является далеко не очевидным. Рассмотрим методы ответа на этот вопрос.
Таким образом, упрощение сложного числового выражения позволяет определить, рационально ли заданное им число.
Теперь разберемся со знаком корня.
5 = 2 log 2 5 = 2 m n 5 n = 2 m
Очевидно, последнее равенство невозможно так как в левой и правой частях находятся соответственно нечетное и четное числа. Следовательно, сделанное предположение неверно, и число log 2 5 не является рациональным числом.
Какие числа называют рациональными в математике
Рациональные числа в математике — какие так называются
Множество рациональных чисел не бесконечно, существуют примеры исключений. Доказательством тому служит множество иррациональных чисел. К примеру, рациональными не считают:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для чего нужны, какой буквой обозначается
Для обозначения множества рациональных чисел используют букву Q. Это множество можно записать в виде:
Название множества произошло от латинского слова «ratio», которое означает «отношение», «дробь». То есть рациональные числа — это дробные числа. Их применяют при счете целых объектов и их частей — например, если порезать яблоко на несколько долек.
Свойства рациональных чисел
Одно из основных свойств рациональных чисел — их замкнутость относительно всех арифметических операций.
Это свойство можно объяснить на примере натуральных чисел: 16+14=30. 30 — это натуральное число, как и его слагаемые. Это значит, что множество натуральных чисел замкнуто относительно операции сложения.
С помощью рациональных чисел можно выполнять любые арифметические операции:
Таким образом, множество Q замкнуто относительно всех четырех операций.
Список свойств рациональных чисел широк. Его можно сократить до нескольких основных пунктов.
Классификация рациональных чисел, виды с примерами
Выделяют несколько групп рациональных чисел.
Какая разница между целыми, натуральными и рациональными числами
Натуральные числа — это все целые числа, начиная с 1. Их множество обозначают буквой N.
1, 14, 47 относятся к натуральным числам.
Это понятие появилось раньше других. Натуральные числа используют для простого счета существующих в окружающем мире предметов. Ноль, отрицательные и дробные числа не входят в множество N. Оно замкнуто относительно операций сложения и умножения.
Целые числа включают в себя натуральные числа, а также ноль и числа, противоположные натуральным — отрицательные. Их множество обозначают буквой Z.
Исторически целые числа возникли как решение проблемы ограниченности натуральных чисел. С развитием математики стало известно о существовании нуля и отрицательных чисел. Однако множество Z не включает в себя дробные числа. Оно замкнуто относительно всех операций, кроме деления.
Множество рациональных чисел, исходя из определения, является наиболее широким из трех. Оно включает в себя все натуральные и целые числа.
Систему отношений между множествами можно представить в виде кругов Эйлера. Схема представлена ниже.
«История возникновения рациональных чисел»
Описание презентации по отдельным слайдам:
История возникновения рациональных чисел
С рациональными числами люди знакомились постепенно. Вначале при счёте предметов возникли натуральные числа. Учёные полагают, что слово для обозначения сотни появилось более 7000 лет назад, для обозначения тысячи – 6000 лет назад, а 5000 лет тому назад в Древнем Египте и в Древнем Вавилоне появляются названия для громадных чисел – до миллиона. Но долгое время натуральный ряд чисел считался конечным: люди думали, что существует самое большое число.
Величайший древнегреческий математик и физик Архимед (287-212г. до н.э.) придумал способ описания громадных чисел. Самое большое число, которое умел называть Архимед, было настолько велико, что для его цифровой записи понадобилась бы лента длиннее, чем расстояние от Земли до Солнца.
При разделе добычи и в дальнейшем при измерении величин, да и в других похожих случаях люди встретились с необходимостью ввести «ломаные числа» — обыкновенные дроби. Чтобы облегчить действия с дробями, были придуманы десятичные дроби.
В Европе десятичные дроби ввел в 1585 г. Голландский математик и инженер Симон Стевин.
Отрицательные числа рассматривал греческий математик Диофант, живший в III веке н.э. Ещё раньше с отрицательными числами столкнулись китайские учёные. Это было примерно во II веке н.э.
Отрицательные числа появились позднее, чем дроби. Долгое время такие числа считали «несуществующими», «ложными». Положительные и отрицательные числа служат для описания изменений величин. Если величина растёт, то говорят, что её изменение положительно, а если она убывает, то изменение называют отрицательным.
Спасибо за внимание.
Курс повышения квалификации
Охрана труда
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
Курс профессиональной переподготовки
Охрана труда
Ищем педагогов в команду «Инфоурок»
Номер материала: ДВ-071996
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Костромская область разработала программу привлечения педагогических кадров
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Минтруд представил проект программ переобучения безработных на 2022 год
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Москве новогодние каникулы в школах могут начаться с 27 декабря
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Числа. Рациональные числа.
Какие числа рациональные? Рациональные числа (в отличии от иррациональных)– это числа с положительным или отрицательным знаком (целые и дробные) и ноль. Более точное понятие рациональных чисел, звучит так:
Рациональное число — число, которое представляется обычной дробью m/n, где числитель m — целые числа, а знаменатель n — натуральные числа, к примеру 2/3.
Бесконечные непериодические дроби НЕ входят в множество рациональных чисел.
Поэтому число «Пи» (π = 3,14. ), основание натурального логарифма, e (e = 2,718..) или √2 НЕ являются рациональными числами.
Рациональные числа, примеры:
Множество рациональных чисел.
Множество рациональных чисел обозначают 
Кроме того, одну дробь можно записать разными способами и видами, но значение ее не потеряется. Например, 3/4 и 9/12, (любая дробь, которую можно получить из другой дроби (и наоборот) умножая их либо деля числитель и знаменатель на одинаковое натуральное число, являются одним и тем же рациональным числом). Так как делением числителя и знаменателя дроби на НОД, можем получить единственное представление рационального числа, которое нельзя сократить, то можем говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:
Использование рациональных чисел в реальной жизни.
В реальной жизни множество рациональных чисел используется для счёта частей некоторых целых делимых объектов, например, тортов или других продуктов, которые разрезаются на части перед употреблением, или для грубой оценки пространственных отношений протяжённых объектов.
Свойства рациональных чисел.
Основные свойства рациональных чисел.
Правило суммирования выглядит так:
3. Операция умножения. Для всяких рациональных чисел a и b есть правило умножения, оно ставит им в соответствие определенное рациональное число c. Число c называют произведением чисел a и b и обозначают (a⋅b), а процесс нахождения этого числа называют умножение.
4. Транзитивность отношения порядка. Для любых трех рациональных чисел a, b и c если a меньше b и b меньше c, то a меньше c, а если a равно b и b равно c, то a равно c.
5. Коммутативность сложения. От перемены мест рациональных слагаемых сумма не изменяется.
6. Ассоциативность сложения. Порядок сложения 3-х рациональных чисел не оказывает влияния на результат.
7. Наличие нуля. Есть рациональное число 0, оно сохраняет всякое другое рациональное число при складывании.
8. Наличие противоположных чисел. У любого рационального числа есть противоположное рациональное число, при их сложении получается 0.
9. Коммутативность умножения. От перемены мест рациональных множителей произведение не изменяется.
10. Ассоциативность умножения. Порядок перемножения 3-х рациональных чисел не имеет влияния на итог.
11. Наличие единицы. Есть рациональное число 1, оно сохраняет всякое другое рациональное число в процессе умножения.
12. Наличие обратных чисел. Всякое рациональное число, отличное от нуля имеет обратное рациональное число, умножив на которое получим 1.
13. Дистрибутивность умножения относительно сложения. Операция умножения связана со сложением при помощи распределительного закона:
14. Связь отношения порядка с операцией сложения. К левой и правой частям рационального неравенства прибавляют одно и то же рациональное число.
15. Связь отношения порядка с операцией умножения. Левую и правую части рационального неравенства можно умножить на одинаковое неотрицательное рациональное число.
16. Аксиома Архимеда. Каким бы ни было рациональное число a, легко взять столько единиц, что их сумма будет больше a.