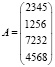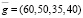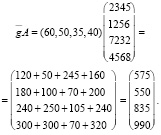Для чего математика в экономике

Математика в экономике

Вы будете перенаправлены на Автор24

Общие сведения о математической науке

Математика представляет собой самостоятельную науку, которая занимается изучением объектов и отношений между ними посредством подсчёта, измерения и описания их форм, в основе чего лежат сведения о некоторых (пространственных или количественных) свойствах объектов, оформленных в виде аксиом.

Одной из наиболее важных научных дисциплин, результаты которой используются практически во всех сферах профессиональной и повседневной деятельности людей, является математика.

Математика признана фундаментальной научной дисциплиной, которая предоставляет другим наукам язык и методы исследования. Благодаря их применению обнаруживается структурная взаимосвязь между разными научными направлениями и существование общих законов природы.

Математика также считается комплексной наукой, которая рассматривается как совокупность нескольких взаимосвязанных, но самостоятельных дисциплин. Ключевыми из них являются арифметика, алгебра, геометрия (элементарная, аналитическая, дифференциальная), математический анализ, теория вероятностей и др. Они предоставляют широкий инструментарий для всестороннего изучения объектов различной природы.

Благодаря математической науке было обеспечено прорывное развитие различных сфер человеческой деятельности. В том числе это касается и экономической деятельности людей.

Применение методов математики в экономических науках

Экономика представляет собой науку, которая изучает объективные причины и условия ведения в обществе хозяйственной деятельности. В этой связи экономике изначально были присущи различные количественные характеристики, исследование и описание которых потребовало использование большого числа математических методов.

Экономические объекты, процессы и явления изучаются математически формализованным образом. Роль математики в экономике заключается в том, что ее язык позволяет сформулировать содержательные и проверяемые гипотезы о многих сложных экономических явлениях. Причем большая часть этих явлений вообще не может быть изучена без привлечения математического аппарата. В частности, его использование привело к созданию математических моделей, в которых нашли отражение некоторые теоретические экономические взаимосвязи.

Готовые работы на аналогичную тему

Область применения математического аппарата к экономическим явлениям принято называть математической экономикой. На данный момент её чаще всего рассматривают как совокупность следующих разделов:

Это одна из классификаций математических методов, используемых в экономике. В научной литературе предлагают другие варианты их классификации и систематизации, однако суть во многом остается одна и та же.

Характеристика разделов современной математической экономики

В основе современной экономики лежит масштабное применение методов математического анализа и матричной алгебры. Нередко экономические задачи включает в себя большое число переменных и нахождение решения этой задачи оказывается возможным только с помощью математики. Это требует от экономистов существенной математической подготовки. Сейчас уже обычным делом является получение высшего экономического образования как второго дипломированными математиками.

В экономике можно выделить несколько направлений, которые образованы в результате использования математических методов и моделей:

Математический аппарат начал применяться при решении вопросов удовлетворения общественных нужд ещё в XVII веке. Однако тогда этот опыт был фрагментарным, использовался от случая к случаю. Масштабное внедрение математики в экономику было вызвано движением маржинальной экономической школы, представители которого решали задачи оптимизации производства и потребления.

Источник

Для чего математика в экономике

Математика и экономика – это самостоятельные отрасли знаний, каждая из которых обладает своим объектом и предметом исследования. Математика – наука о структурах, порядке и отношениях, которая исторически сложилась на основе операций подсчёта, измерения и описания форм реальных объектов.

Экономика – хозяйственная деятельность общества, а также совокупность отношений, складывающихся в системе производства, распределения, обмена и потребления.

С древних времен и вплоть до XIX века математикой занимались лишь избранные. Развитию математики, а в частности именно в инженерных направлениях, способствовала промышленная революция, которая вызвала потребность в усовершенствовании и создании различных механизмов и различных разновидностей машин. Большой прорыв был сделан во второй половине прошлого века, когда достижения в области ядерной физики повлекли за собой дальнейшее развитие математики, математического образования и высокопроизводительных вычислений [3]. Подобные явления происходят и в наши дни, когда возникла необходимость управления многими социальными и различными экономическими процессами, которые являются предпосылкой к очередному витку в развитии математики. Экономика как наука в течение многих лет не вызывала внимание математиков, хотя есть единичные примеры математических работ XIX век, которые связанные с экономикой. В настоящее время в некоторых странах, а особенно в США, наблюдается процесс миграции многих ученых из классических для математики прикладных областей в экономику.

На сегодняшний день обширное использование математического аппарата в своих исследованиях способствует достижению наибольших успехов в данных областях. Поэтому применение математики на практике позволяет достичь более значительных результатов в изучении определенных явлений природы и общества [4].

Особенности математики, как отличительной области знаний, которые делают ее неповторимой, заключаются в следующем:

– не допущение никаких расхождений в определение правил и создания отношений – математических формул;

– математические формулы составляются из ряда аксиом, на основе строгих условий;

– возможность владеть теми или другими понятиями, не раскрывая их смысла [2].

Именно благодаря всем выше перечисленным особенностям математический аппарат и делается для всех отраслей знаний многофункциональным аналитическим инструментом.

Малоизвестные задачи, которые ставит экономика перед математикой, способствует ее стимулированию в поиске способов их решения. Потребности экономики на данный момент в новых математических методах превосходят способности математики [7]. Происхождение новых направлений в прикладной математике таких как: теории игр, программирования, массового обслуживания и некоторые другие – это экономическая действительность.

Развитию высокопрофессиональных знаний различных специалистов в отрасли экономики и управления способствует познание многих математических методов и это прежде всего характерный элемент развития. Именно кадровые работники являются пользователями различных аналитических инструментов, созданных математикой, следовательно, и обучать их математике нужно как пользователей, а не как математиков, объясняя им сущность математических терминов.

Для экономического анализа, статистических расчетов, организации различных внутрипроизводственных хозрасчетов и сокращения документа оборота предприятий и организаций все шире используют в экономической практике матричные методы, благодаря простоте их формул и богатому экономическому содержанию [6].

Матрицей называется таблица размером m×n прямоугольной формы состоящая из чисел и содержащая m количество строк и n количество столбцов и имеющая вид [1]:

A = .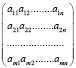

Рассмотрим самое простое применение матрицы в различных отраслях экономики.

Возьмем предприятие, которое выпускает 4 вида изделий с использованием 4-х видов сырья. Нормы расхода сырья даны как элементы матрицы А. Вид сырья: 1, 2, 3, 4.

Требуется найти затраты сырья на каждый вид изделия при заданном плане их выпуска: при 60, 50, 35 и 40 ед.

Для начала составим вектор-план выпуска продукции

Тогда решение задачи дается вектором затрат, координаты которого и являются величинами затрат сырья по каждому его виду; данный вектор затрат вычисляется как произведение вектора 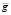на матрицу А:

В этой задаче мы смогли с помощью матрицы составить ближайший план выпуска продуктов выполняемым предприятием по выпуску 4 продуктов из 4 видов сырья [9].

Экономико-математические методы это обобщающее название комплекса экономических и математических научных дисциплин, объединенных для изучения социально-экономических систем и процессов.

Основным методом исследования систем является метод моделирования, т. е. способ теоретического анализа и практического действия, направленный на разработку и использование моделей. При этом под моделью понимают математическое описание исследуемого экономического процесса или объекта, которое выражает закономерности экономических процессов в абстрактном виде с помощью математических соотношений [2].

Рассмотрим задачу определения оптимального ассортимента продукции.

Предприятие изготавливает два вида продукции – П1 и П2 которые поступают в оптовую продажу. Для производства продукции используются два вида сырья – А и В. Максимально возможные запасы сырья в сутки составляют 9 и 13 единиц соответственно. Расход сырья на единицу продукции вида П1 и вида П2 дан в таблице.

Опыт работы показал, что суточный спрос на продукцию П1 никогда не превышает спроса на продукцию П2 более чем на 1 ед. Кроме того, известно, что спрос на продукцию П2 никогда не превышает 2 ед. в сутки. Оптовые цены единицы продукции равны: 3 д. е. – для П1 и 4 д. е.
для П2.

Источник

ВЗАИМОДЕЙСТВИЕ МАТЕМАТИКИ С ЭКОНОМИКОЙ

В нынешнее время наивысших успехов достигают те области знаний, которые наиболее обширно пользуются математическим аппаратом в своих исследованиях. Что же позволяет при применении математики на практике достигать значительных результатов в изучении явлений природы и общества? Ведь математика владеет такими терминами, которые, на первый взгляд, не имеют никакого прямого отношения к действительной жизни: матрицы, интегралы, уравнения и т.д.

Математика, как отличительная область знаний имеет особенности, которые делают ее неповторимой. Они состоят в следующем:

— строжайшее, не допускающее никаких расхождений определение правил создания отношений – математических формул;

— при выводе формул сначала составляется ряд аксиом, а затем, исходя из них, на основе строжайших условий составляются математические формулы;

— возможность владеть теми или другими понятиями, не раскрывая их смысла.

Именно выше приведенные особенности и делают математический аппарат многофункциональным аналитическим инструментом для всех отраслей знаний.

Таким образом, владея данными свойствами, математика на основе выдвинутых предположений, используя строжайшие логические правила, позволяет приобретать новейшие знания об изучаемом предмете, вторично применяя надлежащие правила, получать новоприобретенные знания и т.д. Другими словами с помощью математических преобразований на основе выдвинутых гипотез и строжайших логических правил можно установит новейшие свойства и отношения действительных объектов, которые следом могут подтвердиться эмпирически. Это и делает математику державной наукой. Как отмечал Карл Маркс, наука только тогда достигает совершенства, когда ей удается пользоваться математикой.

Для того чтобы, извлечь с помощью математических моделей нынешнюю информацию, удовлетворяющую настоящей действительности, нужно формировать на основе содержащихся знаний качественные гипотезы, закладываемые в модель. В экономике математика применяется достаточно недавно, а именно с того времени, когда великий экономист Франсуа Кене изобрел и первоиздал свои экономические таблицы. Это первый опыт описания количественного процесса воспроизведения социального продукта как единого целого. Впоследствии Адам Смит предложил классическую макроэкономическую модель социального воспроизведения. Карл Маркс, в принадлежавших ему работах, достаточно масштабно использовал математический аппарат.

В политической экономике XIX века зародилась математическая школа, представителями которой были Л. Вальрас, О. Курно, А. Маршалл и другие. Они одни из первых, кто попытался пользоваться математическим аппаратом в изучении механизма функционирования рынка. Следом, за этими выдающимися экономистами, математические методы начинают использовать и русские ученые – экономисты, такие как В.И. Дмитриев, И.П. Кондратьев, Е. Слуцкий.

При возникновении государственного планирования в 1920-е гг. вопрос использования математического аппарата в экономике становится предметом острейших споров. Тем не менее, начиная с 1940-х по 1960-е гг. тема применения математики в экономике России почти не рассматривалась. Имеющиеся на тот момент времени математические методы регулирования планово-экономических задач в действительности не использовались. В середине 40-х гг. XX столетия в развитых зарубежных странах начинается молниеносный процесс внедрения математики в экономику, как в сферу научных исследований, так и в отрасль управления бизнесом. В СССР к использованию математического аппарата возвращаются только в конце 50-х годов текущего века.

В настоящее время становление микро- и макроэкономики прикладных экономических предметов связано с наиболее важным этапом их формализации. Начало для этого заложил прогресс в разделе прикладной математики и в сфере информационных технологий, позволивший обрабатывать, передавать и хранить большие массивы информации.

В процессе развития экономико-математического моделирования, осуществляется взаимодействие двух систем высоконаучных знаний – экономических и математических. Между экономикой и математикой существует как прямая, так и противоположная связь, а именно: возникновение новейшего математического аппарата и его использование на практике, позволяет экономике творчески решать существующие вопросы. Вследствие математического моделирования удалось увеличить и углубить воззрение экономистов о способах координирования управленческих заключений по ряду критериев оптимальности, об особенности целеполагания как в разработках, так и в действительности управления на разных стадиях.

Экономика ставит перед математикой малоизвестные задачи и заинтересовывает ее в поиске способов их решения. На данный момент потребности экономики в новых математических методах опережают способности математики. Экономическая действительность вызвала происхождение целых направленностей в прикладной математике – теории игр, программирования, массового обслуживания и др.

Познание математических методов становится характерным элементом развития высокопрофессиональных знаний специалистов в отрасли экономики и управления. Эти кадровые работники являются фактическими пользователями аналитических инструментов, созданных математикой, таким образом, и обучать их математике нужно как пользователей, а не как математиков, объясняя им сущность математических терминов. При использовании аналитических инструментов необходимо сказать о возможной области их использования в экономике. Нам известно, что в актуальной на сегодняшний день ситуации в связи с увеличением значимости прикладной математики в экономике, происхождением новейших спецтехнологий математической обработки информации обязательной необходимостью является пересмотр содержания курсов по математике. Пользователю требуется знать, не как именно получена математическая формула, а то где и при каких условиях она может быть применена в экономике.

Вследствие всего выше изложенного, можно сделать вывод, что две совершенно разные науки, такие как экономика и математика тесно взаимодействуют между собой. Фактическое применение математики в экономических исследованиях, позволяющее объяснить прошлое, увидеть будущее и оценить результат своих действий, потребует значительных усилий, которых на данный момент в экономике не хватает.

Канторович А.В. Оптимальные решения в экономике/ А.В. Канторович, А.Б. Горетко – М.: Наука 2009. – 379 с.

Красс М.С. Математика для экономистов/ Красс М.С., Чупрынов Б.П. – СПб.: Питер, 2011. – 469 с.

Канторович А.В. О состоянии и задачах экономической науки. – М.: Наука.- 2010. – 296 с.

Невидомская И.А., Якубова А.М.Применение факторного анализа при исследовании экономических процессов //Современные наукоемкие технологии. 2013. № 6. С. 81-83.

Источник

Выступление по теме: «МАТЕМАТИКА В ЭКОНОМИКЕ»

МАТЕМАТИКА В ЭКОНОМИКЕ

Понятие «экономист» сродни понятию «доктор», оно также разнообразно. Есть макроэкономика и микроэкономика, есть экономика труда и региональная экономика. Но общим у них является одна вещь. Экономика изучает закономерности в потоках товаров и денег. Ну а поскольку эти потоки надо анализировать, то сначала их надо подсчитать, классифицировать, убрать ошибки. Потом надо подумать «а почему они идут именно так», то есть придумать какую-то теорию, ну а затем ее проверить реальными цифрами.

Если делать такой анализ без цифр (то есть без математики), то никакого реального ответа ты не получишь. Поэтому, конечно, экономистам математика нужна очень сильно, особенно, когда приходится анализировать огромное количество товаров, потребителей и производителей. Без математики тут просто не обойдешься.

Разве можно представить современного финансового аналитика без использования различных математических методов? Взять хотя бы анализ фондовых рынков, ведь колебания курса акций, обменного курса валют подвержены определенным математическим законам. И если человек в достаточной мере знаком с математикой, он может делать правильные прогнозы. И соответственно, различные эконометрические модели, играющие сейчас важную роль, строятся на математических параметрах. Если человек умеет грамотно анализировать ту ситуацию, которая существует сегодня на рынке, он может рассчитать, например, величину прибыли своего предприятия и многое другое. Многие вещи базируются на математических методах, ведь не зря мы изучаем на втором и третьем курсе экономико-математические методы и модели.

Математика нужна экономистам по двум причинам. Она существенно облегчает сравнение «на пределе» и позволяет анализировать данные.

Рассмотрим простой пример. Представьте, что вас интересует, как изменится цена килограмма говяжьей вырезки, пакета молока и бутылки оливкового масла после введения санкций.

На сколько же вырастут цены? Здесь и помогает математика!

Так математика помогает экономистам делать прогнозы по экономическому росту, выпуску, ценам, уровню заработных плат и т.д. И, конечно, проводить экономическую политику. Представьте, что вы решаете, вводить ли санкции на импорт продуктов, и хотели бы узнать, во сколько они обойдутся потребителям, сколько заработают магазины, поставщики и т.п. Для этого экономистам и нужна математика.

Экономист использует в своих расчётах прикладную математику, которая невозможна без знания её фундаментальных основ.

Хороший экономист обязан уметь проводить сложные расчеты, чтобы управлять процессами, ему не обойтись без этих знаний при составлении планов (в том числе без использования передовых методов: теории игр, нечетких множеств и т.д.)

Математика. Этот предмет важен для любого экономиста, ведь эта профессия напрямую связана с цифрами, графиками, формулами и статистическими данными.

Математика- это краеугольный камень, на котором держится весь свод человеческих знаний. Бухгалтерия невозможна и нереализуема без применения математики. Пачоли (Pacioli)Лука (1445-1517), итальянский математик рассматривал бухгалтерский учёт как частный случай прикладной математики.

Современное общество, имея высокоразвитую систему товарно-денежных отношений, испытывает все возрастающую потребность в специалистах, выполняющих работу по бухгалтерскому учету. Человек этой профессии является не просто сотрудником в финансовом отделе предприятия или организации, это один из важнейших элементов, которые позволяют контролировать устойчивость и правильность механизма бизнеса.

Бухгалтерское дело очень нужное и важное. Если не вести учет доходов и расходов, то порядка в работе организации не будет! Кроме того, без бухгалтерского учета государство не могло бы контролировать работу предприятия.

Из математики бухгалтерский учёт позаимствовал одну из главных своих качествточность.

Математическая модель бухгалтерского учёта понятна и принята специалистами в любой стране мира, т.к. язык математики обладает необходимым единообразием в понимании. Глобальная математическая модель бухгалтерского учёта и формирование финансовой отчётности – это ключ к взаимопониманию между бухгалтерами. Бухгалтерия и математика, по сути, неразделимы. Не может быть никакой бухгалтерии без знания математики.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник

МАТЕМАТИКА И ЭКОНОМИКА: ИХ ВЗАИМОСВЯЗИ

Экономика – хозяйственная деятельность общества, а также совокупность отношений, складывающихся в системе производства, распределения, обмена и потребления.

С древних времен и вплоть до XIX века математикой занимались лишь избранные. Развитию математики, а в частности именно в инженерных направлениях, способствовала промышленная революция, которая вызвала потребность в усовершенствовании и создании различных механизмов и различных разновидностей машин. Большой прорыв был сделан во второй половине прошлого века, когда достижения в области ядерной физики повлекли за собой дальнейшее развитие математики, математического образования и высокопроизводительных вычислений. Подобные явления происходят и в наши дни, когда возникла необходимость управления многими социальными и различными экономическими процессами, которые являются предпосылкой к очередному витку в развитии математики. Экономика как наука в течение многих лет не вызывала внимание математиков, хотя есть единичные примеры математических работ XIX век, которые связанные с экономикой. В настоящее время в некоторых странах, а особенно в США, наблюдается процесс миграции многих ученых из классических для математики прикладных областей в экономику.

На сегодняшний день обширное использование математического аппаратом в своих исследованиях способствует достижению наибольших успехов в данных областях. Поэтому применение математики на практике позволяет достичь более значительных результатов в изучении определенных явлений природы и общества.

Особенности математики, как отличительной области знаний, которые делают ее неповторимой, заключаются в следующем:

— не допущение никаких расхождений в определение правил и создания отношений – математических формул;

— математические формулы составляются из ряда аксиом, на основе строгих условий;

— возможность владеть теми или другими понятиями, не раскрывая их смысла.

Именно благодаря всем выше перечисленным особенностям математический аппарат и делается для всех отраслей знаний многофункциональным аналитическим инструментом.

Малоизвестные задачи, которые ставит экономика перед математикой способствует ее стимулированию в поиске способов их решения. Потребности экономики на данный момент в новых математических методах превосходят способности математики. Происхождение новых направлений в прикладной математике таких как: теории игр, программирования, массового обслуживания и некоторые др. – это экономическая действительность.

Развитию высокопрофессиональных знаний различных специалистов в отрасли экономики и управления способствует познание многих математических методов и это прежде всего характерный элемент развития. Именно кадровые работники являются пользователями различных аналитических инструментов, созданных математикой, следовательно, и обучать их математике нужно как пользователей, а не как математиков, объясняя им сущность математических терминов.

Для экономического анализа, статистических расчетов, организации различных внутрипроизводственных хозрасчетов и сокращения документа оборота предприятий и организаций все шире используют в экономической практике матричные методы, благодаря простоте их формул и богатому экономическому содержанию.

Матрицей называется таблица размером m×n прямоугольной формы состоящая из чисел и содержащая m количество строк и n количество столбцов и имеющая вид:

Рассмотрим самое простое применение матрицы в различных отраслях экономики.

Возьмем предприятие, которое выпускает 4 вида изделий с использованием 4-х видов сырья. Нормы расхода сырья даны как элементы матрицы А. Вид сырья: 1, 2, 3, 4.

Требуется найти затраты сырья на каждый вид изделия при заданном плане их выпуска: при 60, 50, 35 и 40 ед.

Решение. Для начала составим вектор-план выпуска продукции

Тогда решение задачи дается вектором затрат, координаты которого и являются величинами затрат сырья по каждому его виду; данный вектор затрат вычисляется как произведение вектора на матрицу А:

В этой задаче мы смогли с помощью матрицы составить ближайший план выпуска продуктов выполняемым предприятием по выпуску 4 продуктов из 4 видов сырья.

Таким образом, можно сделать существенный вывод, что две совершенно разные науки, такие как экономика и математика тесно взаимодействуют друг с другом. Узконаправленные математики или экономисты на сегодняшний день не нужны, а нужны подготовленные в двух различных направлениях специалисты. Все выше изложенное будет способствовать переходу к разработке разнообразных экономических программ с математической точностью и глубокими экономическими знаниями.

1. Гулай Т.А., Жукова В.А., Мелешко С.В., Невидомская И.А. Математика /Рабочая тетрадь. Ставрополь, 2015.

2. Гулай Т.А., Долгополова А.Ф., Мелешко С.В. Математические методы исследования экономических процессов //Международный журнал экспериментального образования. 2016. № 12-1. С. 116-117

3. Гулай Т.А., Невидомская И.А., Мелешко С.В. Анализ и оценка приоритетности разделов дисциплины «математический анализ» изучаемой студентами инженерных направлений // European Social Science Journal. 2013. № 8-2 (35). С. 109-115.

4. Коннова Д.А., Леликова Е.И., Мелешко С.В. Взаимодействие математики с экономикой //Современные наукоемкие технологии. 2014. № 5-2. С. 159-161.

5. Линейная алгебра (учебное пособие) / Крон Р.В., Попова С.В., Долгих Е.В., Смирнова Н.Б. // Международный журнал экспериментального образования. 2014. № 11-1. С. 115.

6. Линейная алгебра / Крон Р.В., Попова С.В., Смирнова Н.Б., Долгих Е.В. // учебное пособие для студентов вузов сельскохозяйственных, инженерно-технических и экономических направлений / Москва, 2015.

8. Светличная В.Ю., Орехова Н.В., Мелешко С.В. Применение элементов линейной алгебры в экономике //Современные наукоемкие технологии. 2014. №5-2. С. 174-175.

9. Сизова С.А., Мурдугова В.Ю., Мелешко С.В Линейное программирование как область математического программирования при решении экономических задач. //Theoretical & Applied Science. 2013. № 6 (2). С. 16-20.

10. Яновский А.А., Литвин Д.Б Математика /Учебное пособие. Ставрополь. 2015. Том 1.

Источник