Для чего нужен формальный язык
Формальные языки и грамматики
Мотивация
Время от времени на Хабре публикуются посты и переводные статьи, посвященные тем или иным аспектам теории формальных языков. Среди таких публикаций (не хочется указывать конкретные работы, чтобы не обижать их авторов), особенно среди тех, которые посвящены описанию различных программных инструментов обработки языков, часто встречаются неточности и путаница. Автор склонен считать, что одной из основных причин, приведших к такому прискорбному положению вещей, является недостаточный уровень понимания идей, лежащих в основании теории формальных языков.
Этот текст задуман как популярное введение в теорию формальных языков и грамматик. Эта теория считается (и, надо сказать, справедливо) довольно сложной и запутанной. На лекциях студенты обычно скучают и экзамены тем более не вызывают энтузиазма. Поэтому и в науке не так много исследователей в этой тематике. Достаточно сказать, что за все время, с зарождения теории формальных грамматик в середине 50-х годов прошлого века и до наших дней, по этому научному направлению было выпущено всего две докторских диссертации. Одна из них была написана в конце 60-х годов Алексеем Владимировичем Гладким, вторая уже на пороге нового тысячелетия — Мати Пентусом.
Далее в наиболее доступной форме описаны два основных понятия теории формальных языков: формальный язык и формальная грамматика. Если тест будет интересен аудитории, то автор дает торжественное обещание разродиться еще парой подобных опусов.
Формальные языки
Коротко говоря, формальный язык — это математическая модель реального языка. Под реальным языком здесь понимается некий способ коммуникации (общения) субъектов друг с другом. Для общения субъекты используют конечный набор знаков (символов), которые проговариваются (выписываются) в строгом временном порядке, т.е. образуют линейные последовательности. Такие последовательности обычно называют словами или предложениями. Таким образом, здесь рассматривается только т.н. коммуникативная функция языка, которая изучается с использованием математических методов. Другие функции языка здесь не изучаются и, потому, не рассматриваются.
В качестве известного примера такой математической абстракции можно привести модель, известную под неблагозвучным для русского уха названием «мешок слов». В этой модели исследуются тексты естественного языка (т.е. одного из тех языков, которые люди используют в процессе повседневного общения между собой). Основной объект модели мешка слов — это слово, снабженное единственным атрибутом, частотой встречаемости этого слова в исходном тексте. В модели не учитывается, как слова располагаются рядом друг с другом, только сколько раз каждое слово встречается в тексте. Мешок слов используется в машинном обучении на основе текстов в качестве одного из основных объектов изучения.
Но в теории формальных языков представляется важным изучить законы расположения слов рядом друг с другом, т.е. синтаксические свойства текстов. Для этого модель мешка слов выглядит бедной. Поэтому формальный язык задается как множество последовательностей, составленных из элементов конечного алфавита. Определим это более строго.
Алфавит представляет собой конечное непустое множество элементов. Эти элементы будем называть символам. Для обозначения алфавита обычно будем использовать латинское V, а для обозначения символов алфавита — начальные строчные буквы латинского алфавита. Например, выражение V =
Цепочка представляет собой конечную последовательность символов. Например, abc — цепочка из трех символов. Часто при обозначении цепочек в символах используют индексы. Сами цепочки обозначают строчными символами конца греческого алфавита. Например, omega = a1. an — цепочка из n символов. Цепочка может быть пустой, т.е. не содержать ни одного символа. Такие цепочки будем обозначать греческой буквой эпсилон.
Наконец, формальный язык L над алфавитом V — это произвольное множеств цепочек, составленных из символов алфавита V. Произвольность здесь означает тот факт, что язык может быть пустым, т.е. не иметь ни одной цепочки, так и бесконечным, т.е. составленным из бесконечного числа цепочек. Последний факт часто вызывает недоумение: разве имеются реальные языки, которые содержат бесконечное число цепочек? Вообще говоря, в природе все конечно. Но мы здесь используем бесконечность как возможность образования цепочек неограниченной длины. Например, язык, который состоит из возможных имен переменных языка программирования C++, является бесконечным. Ведь имена переменных в C++ не ограничены по длине, поэтому потенциально таких имен может быть бесконечно много. В реальности, конечно, длинные имена переменных не имеют для нас особого смысла т.к. к концу чтения такого имени уже забываешь его начало. Но в качестве потенциальной возможности задавать неограниченные по длине переменные, это свойство выглядит полезным.
Итак, формальные языки — это просто множества цепочек, составленных из символов некоторого конечного алфавита. Но возникает вопрос: как можно задать формальный язык? Если язык конечен, то можно просто выписать все его цепочки одну за другой (конечно, можно задуматься, имеет ли смысл выписывать цепочки языка, имеющего хотя бы десять тысяч элементов и, вообще, есть ли смысл в таком выписывании?). Что делать, если язык бесконечен, как его задавать? В этот момент на сцену выходят грамматики.
Формальные грамматики
Способ задания языка называет грамматикой этого языка. Таким образом, грамматикой мы называем любой способ задания языка. Например, грамматика L =
Назначение грамматики — задание языка. Это задание обязательно должно быть конечным, иначе человек не будет в состоянии эту грамматику понять. Но каким образом, конечное задание описывает бесконечные совокупности? Это возможно только в том случае, если строение всех цепочек языка основано на единых принципов, которых конечное число. В примере выше в качестве такого принципа выступает следующий: «каждая цепочка языка начинается с символов a, за которыми идет столько же символов b». Если язык представляет собой бесконечную совокупность случайным образом набранных цепочек, строение которых не подчиняется единым принципам, то очевидно для такого языка нельзя придумать грамматику. И здесь еще вопрос, можно или нет считать такую совокупность языком. В целях математической строгости и единообразия подхода обычно такие совокупности языком считают.
Итак, грамматика языка описывает законы внутреннего строения его цепочек. Такие законы обычно называют синтаксическими закономерностями. таким образом, можно перефразировать определение грамматики, как конечного способа описания синтаксических закономерностей языка. Для практики интересны не просто грамматики, но грамматики, которые могут быть заданы в рамках единого подхода (формализма или парадигмы). Иначе говоря, на основе единого языка (метаязыка) описания грамматик всех формальных языков. Тогда можно придумать алгоритм для компьютера, который будет брать на вход описание грамматики, сделанное на этом метаязыке, и что-то делать с цепочками языка.
Такие парадигмы описания грамматик называют синтаксическими теориями. Формальная грамматика — это математическая модель грамматики, описанная в рамках какой-то синтаксической теории. Таких теорий придумано довольно много. Самый известный метаязык для задания грамматик — это, конечно, порождающие грамматики Хомского. Но имеются и другие формализмы. Один из таких них — окрестностные грамматики, будет описан чуть ниже.
Окрестностные грамматики
В середине 60-х годов советский математик Юлий Анатольевич Шрейдер предложил простой способ описания синтаксиса языков на основе т.н. окрестностных грамматик. Для каждого символа языка задается конечное число его «окрестностей» — цепочек, содержащих данный символ (центр окрестности) где-то внутри. Набор таких окрестностей для каждого символа алфавита языка называется окрестностной грамматикой. Цепочка считается принадлежащей языку, задаваемому окрестностной грамматикой, если каждый символ этой цепочки входит в нее вместе с некоторой своей окрестностью.
Не всякий язык может быть описан окрестностной грамматикой. Рассмотрим, например, язык B, цепочки которого начинаются либо с символа «0», либо с символа «1». В последнем случае далее в цепочке могут идти символы «a» и «b». Если же цепочка начинается с нуля, то далее могут идти только символы «a». Нетрудно доказать, что для этого языка нельзя придумать никакой окрестностной грамматики. Легитимность вхождения символа «b» в цепочку обусловлена ее первым символом. Для любой окрестностной грамматики, в которой задается связь между символами «b» и «1» можно будет подобрать достаточно длинную цепочку, чтобы всякая окрестность символа «b» не доставала до начала цепочки. Тогда в начало можно будет подставить символ «0» и цепочка будет принадлежать языку A, что не отвечает нашим интуитивным представлениям о синтаксическом строении цепочек этого языка.
С другой стороны, легко можно построить конечный автомат, который распознает этот язык. Значит, класс языков, которые описываются окрестностными грамматиками, уже класса автоматных языков. Языки, задаваемые окрестностными грамматиками, будем называть шрейдеровскими. Таким образом, в иерархии языков можно выделить класс шрейдеровских языков, который является подклассом автоматных языков.
Можно сказать, что шрейдеровские языки задают одно простое синтаксическое отношение — «быть рядом» или отношение непосредственного предшествования. Отношение дальнего предшествования (которое, очевидно, присутствует в языке B) окрестностной грамматикой задано быть не может. Но, если визуализировать синтаксические отношения в цепочках языка, то для диаграмм отношений, в которые превращаются такие цепочки, можно придумать окрестностную грамматику.
Преимущества изучения формальных языков
Рубрика: Информационные технологии
Дата публикации: 25.04.2020 2020-04-25
Статья просмотрена: 90 раз
Библиографическое описание:
Смирнова, А. Ю. Преимущества изучения формальных языков / А. Ю. Смирнова. — Текст : непосредственный // Молодой ученый. — 2020. — № 17 (307). — С. 29-32. — URL: https://moluch.ru/archive/307/69233/ (дата обращения: 23.12.2021).
Человек, который хочет начать программировать, обращается в интернет, с вопросом: «С чего начать изучение программирования?» В данной анализируется, какие преимущества может получить программист, изучив формальные языки как до освоения первого языка высоко уровня, так и после.
Ключевые слова: язык, язык программирования, правило грамматики, синтаксис языка
В современном мире информационно-компьютерные технологии используются повсеместно. Вследствие этого есть потребность как в самих технологиях, так и в людях, программистах, которые создают программные продукты или их поддерживают. [1] Профессия программиста набирает всё большую популярность, поскольку актуальна и обладает низким порогом вхождения.
Человек, который хочет начать программировать, обращается в интернет, с вопросом: «С чего начать изучение программирования?» Большинство людей советуют начать с конкретного языка программирования, если быть точнее, с курсов по этому языку. [2] В случае, если вопросом интересуется ребёнок, то таким языком является Scratch, если интересуется взрослый, то в зависимости от интересующей его области программирования предлагается наиболее простой язык. Дополнительно советуют углублённо изучать информатику, математику и английский язык в школе и соответствующие им предметы в университете.
В данной статье рассматриваются основные понятия из области формальных языков, а также даётся ответ на вопрос, какие преимущества получит обучающийся, изучив данную область даже до освоения конкретного языка программирования высокого уровня.
Формальный язык — это созданный человеком, искусственный, язык, характеризующийся чёткими и однозначными правилами построения выражений и их интерпретации. [3] В основе формального, как и любого другого языка, лежит алфавит. Алфавит представляет собой конечный набор символов для обмена информацией. Далее описывается и синтаксис языка, т. е. правила построения конкретных выражений.
Наиболее эффективным способом формального описания языков программирования являются грамматики. [4] Грамматикой называется следующая четверка: терминальных символов, нетерминальных символов, правил грамматики и начального символа. Проведя параллель с вышеописанным, терминальные и нетерминальные символы составляют алфавит языка, стартовый символ так же принадлежит алфавиту, синтаксисом языка являются правила грамматики.
За счёт использования формальных грамматик можно описать любой язык программирования. [5] Если проанализировать все языки, можно заметить, что во всех есть некие общие конструкции, некоторые из которых приведены ниже:
Из вышеприведенного анализа можно поговорить о преимуществах изучения формальных языков.
В случае если формальные языки изучаются до того, как приступить к освоению первого языка программирования, преимущество заключается в более быстром пороге вхождения. Это происходит, потому что учащийся знает все конструкции, использующиеся в языке, понимает механизмы их работы и при изучении языка узнаёт только то, как они синтаксически выглядят в конкретном языке.
В случае, когда изучение формальных языков происходит когда учащийся знает уже хотя бы один язык программирования, то преимущество состоит в углублённом понимании конструкций языка и процессов работы программного кода. Важно отметить, что в данном случае при изучении второго, третьего и последующих языков, так же происходит ускорение процесса освоения соответствующего языка. Это происходит за счёт того, что обучающийся знает основу и может легко провести аналогию по уже имеющемуся опыту.
Независимо от времени обучения, знание формальных языков позволяет:
Поговорив о преимуществах, следует отметить и недостатки, которые так же важно учитывать:
Таким образом, проанализировав всю вышеприведённую информацию, можно сделать вывод, что изучение формальных языков даёт программисту ряд преимуществ. Такому человеку легче и быстрее освоить новые языки, он совершает меньше ошибок при написании кода, лучше понимает механизмы работы программ. Однако следует помнить, что детям не стоит начинать свой путь в программировании с изучения формальных языков, а взрослым, которые не понимают или не любят математику, лучше овладевать формальными языками после освоения какого-либо языка программирования.
Формальные языки и грамматики
Математический язык как форма выражения научного знания использовался еще в древности при решении практических задач.
Большую роль в развитии математики как языка – метаязыка наук – сыграла математическая логика, аксиоматизировавшая ряд теории, изучившая их логику, внутреннюю структуру.
Язык как коммуникативный аппарат должен иметь определяющие конструкции слов над данным алфавитом, грамматические правила образования предложений из слов и соотнесения этих предложений тем явлениям и процессам, которые они описывают, или синтаксическим и семантическим правилам.
Пример. В частности, семантика изучает связи вида:
«знак, структура знаков 

синтаксис – связи вида:
«знак, структура знаков 
Пример. Запишем более кратко, сжато, точно (формализованно) факт » целое число x делится на целое число y без остатка». На математическом языке это будет иметь вид «Число x кратно числу y «. Факт, что числа x, y – целые, уже можно специально, как выше, не оговаривать, так как математическое понятие кратности это уже предполагает ( аксиома ). Запишем еще более кратко и формализованно на алгоритмическом языке Паскаль : » x mod y = 0 «. Здесь уже условие кратности область изменения аргументов не нужно оговаривать – они декларированы в языке Паскаль (в описаниях типов и операции mod ).
Языки бывают естественного происхождения (например языки общения) и искусственного происхождения или формальные языки, разрабатываемые для общения человека с автоматом (компьютером) либо для описания и получения знаний.
Язык (множество слов S(X) ) задается грамматикой G(S) – структурой правил, которые позволяют порождать все слова 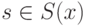
Грамматический анализ – процесс редукции к нетерминальному символу или слову.
Формализованные (формальные) языки
Формальный язык строится в соответствии с четкими правилами, обеспечивая непротиворечивое, точное и компактное отображение свойств и отношений изучаемой предметной области (моделируемых объектов).
В отличие от естественных языков формальным языкам присущи четко сформулированные правила семантической интерпретации и синтаксического преобразования используемых знаков, а также то, что смысл и значение знаков не изменяется в зависимости от каких-либо прагматических обстоятельств (например, от контекста).
Просмотр содержимого документа
«Формализованные (формальные) языки»
ФОРМАЛИЗОВАННЫЕ (ФОРМАЛЬНЫЕ) ЯЗЫКИ
Формальный язык строится в соответствии с четкими правилами, обеспечивая непротиворечивое, точное и компактное отображение свойств и отношений изучаемой предметной области (моделируемых объектов).
В отличие от естественных языков формальным языкам присущи четко сформулированные правила семантической интерпретации и синтаксического преобразования используемых знаков, а также то, что смысл и значение знаков не изменяется в зависимости от каких-либо прагматических обстоятельств (например, от контекста).
Формальные языки часто конструируются на базе языка математики.
На протяжении всей истории развития математики в ней широко использовались символические обозначения для различных объектов и понятий. Однако, наряду с символическими обозначениями ученые-математики свободно пользовались и естественным языком. Но на каком-то этапе развития науки (XVII век) возникла необходимость строгого логического анализа математических суждений, а также уточнения важного для математики понятия “доказательство”. Оказалось, что решить эти задачи невозможно без строгой формализации математических теорий. Появилась потребность в изложении этих теорий на формальном языке. Веком бурного развития различных формальных языков можно считать XX век.
С точки зрения информатики, среди формальных языков наиболее значительную роль играют формальный язык логики (язык алгебры логики) и языки программирования. Они также имеют важное практическое значение.
Прежде всего выбирается алфавит, или совокупность исходных символов, из которых будут строиться все выражения языка. Затем описывается синтаксис языка, то есть правила построения осмысленных выражений.
Поскольку понятие “символ” имеет многозначную смысловую нагрузку для знаков алфавита чаще применяется термин “буква”. Но следует помнить, что буквами в алфавите формального языка могут быть и буквы алфавитов естественных языков, и скобки, и специальные знаки и т.п.
Из букв, по определенным правилам можно составлять слова и выражения.
Простейшее правило заключается в том, что любую конечную последовательность букв можно считать словом. Фактически слово есть простейшая информационная модель (и оно, разумеется, является конструктивным объектом).
В логико-математических языках среди выражений различают термы и формулы.
Из предметных переменных и констант по определенным правилам строятся более сложные термы. Обычно для этого используются допустимые в языке функции.
В логике такими функциями являются инверсия (), конъюнкция (), дизъюнкция (), импликация () и др.
Примеры термов в алгебре логики:
В языках программирования в образовании термов участвуют арифметические операции, операции отношения (,
Примеры термов в языке программирования Pascal:
А; prog_1; ((A1+25)3*B) and (B0)); 2+sqrt(z*sin(b)).
Формулы образуются из термов, к которым применены допустимые в языке операторы.
Примеры логических формул:
Формулами в языке программирования можно назвать операторы программы.
Примеры “формул” языка программирования Pascal:
A:= 2+sqrt(Z*sin(B)); if F3 then write(R) else R:=sqr(F);
Осмысленные выражения получаются в формальном языке, только если соблюдены определенные в языке правила образования, преобразования и “понимания” термов и формул. К таким правилам относятся:
правила построения термов и формул;
правила интерпретации термов и формул (семантический аспект языка);
правила вывода одних формул и термов из других формул и термов.
Для каждого формального языка совокупность этих правил должна быть строго определена и модификация любого из них приводит чаще всего к появлению новой разновидности (диалекта) этого языка.
Оператор языка Pascal
if F3 then write(R) else R:=sqr(F);
интерпретируется в соответствии со следующим правилами:
переменные (простейшие термы) F и R, должны быть ранее определены, то есть ячейки с этими именами должны содержать какие-то значения соответствующего типа (для некоторых версий Pascal это правило не входит в синтаксис языка. В этом случае выбирается та последовательность нулей и единиц, которая содержится в ячейках с заданными адресами и интерпретируется как десятичное число);
если значение выражения (сложного терма “F3”), стоящего вслед за ключевым (зарезервированным) словом if, есть “истина” (true), то выполняется оператор, расположенный за ключевым словом then (на экран выводится значение переменной F); если же его значение “ложь” (false), то выполняется оператор, расположенный за ключевым словом else (вычисляется квадрат значения переменной F и результат помещается в ячейку с именем R).
Наличие в синтаксисе формального языка правил вывода термов и формул позволяет выполнять изоморфные преобразования моделей, построенных на базе данного языка. Таким образом формальные языки не только отражают (репрезентируют) ту или иную совокупность уже имеющихся знаний, но являются средством формализации этих знаний, позволяющим путем формальных преобразований получать новые знания. Причем, поскольку преобразования могут проходить только по строгим формальным правилам, построение моделей, изоморфных данной, но дающих новое знание, вполне может быть автоматизировано. Эта возможность широко используется в компьютерных базах знаний, в экспертных системах, в системах поддержки принятия решений.
Формальные языки широко применяются в науке и технике. В процессе научного исследования и практической деятельности формальные языки обычно используются в тесной взаимосвязи с естественным языком, поскольку последний обладает гораздо большими выразительными возможностями. В то же время формальный язык является средством более точного представления знаний, чем естественный язык, а следовательно, средством более точного и объективного обмена информацией между людьми.
При построения формального языка выбирается алфавит, и описывается синтаксис языка.
Выражениями формального языка являются термы и формулы.
Сложные термы строятся по определенным правилам путем применения к простым термам допустимых в языке функций.
Формулы образуются из термов, к которым применены допустимые в языке операторы.
правила построения термов и формул;
правила интерпретации термов и формул;
правила вывода одних формул и термов из других формул и термов.
Важное практическое значение имеют такие формальные языки, как язык логики и языки программирования.
Формальные языки широко используются в науке и технике. Они являются средством более точного и объективного обмена информацией между людьми, чем естественный язык.
Формальные языки не только отражают (репрезентируют) ту или иную совокупность уже имеющихся знаний, но являются средством формализации этих знаний, позволяющим путем формальных преобразований получать новые знания. Эта возможность широко используется в компьютерных базах знаний, в экспертных системах, в системах поддержки принятия решений.
Перечислите, из каких букв состоит алфавит известного вам языка программирования и какие существуют правила для образования простых термов в этом языке.
Если в этом языке программирования зарезервированные слова? Если да, то приведите примеры зарезервированных и не зарезервированных слов.
Что в языках программирования можно рассматривать как термы и формулы?
ОТВЕТ. В алфавит языка программирования входят все символы, которые можно использовать при написании программ.
Термами языка программирования являются идентификаторы, а также выражения, построенные из идентификаторов, констант, знаков арифметических и логических операций, математических и других (определенных в языке) функций, скобок.
Формулами языка программирования являются допустимые в нем операторы: ввода, вывода, присваивания, условный, цикла и т.п.
Если вы изучали основы формальной логики, то:
приведите примеры, когда формальное преобразование логических формул позволяет получить новое знание об исследуемых объектах;
проинтерпретируйте формулу: x ((x) (x)) или (А А) = 1
Что является алфавитом десятичной системы счисления?
Каково основное правило образования (записи) чисел в этой позиционной системе счисления?
ОТВЕТ. Алфавит: десятичные цифры, десятичная точка (или запятая) и знаки плюс и минус. Правило: вес цифры в числе зависит от ее позиции в записи числа.
Каким образом может быть проинтерпретировано слово двоичного алфавита “0100 1001 0100 0110” в известной вам системе программирования (пробелы вставлены для удобства восприятия)?
Графический интерфейс системы Windows содержит такие элементы как пиктограммы или иконки. Можно ли считать, что они входят в алфавит языка пользовательского интерфейса этой системы? Ответ обоснуйте.
РАСШИРЬ СВОЙ КРУГОЗОР
В формальных языках как ни в каких других велика роль знака, понимаемого в широком смысле этого слова. Некоторые аспекты использования знаков рассматривались нами ранее, но есть смысл поговорить об этом более подробно.
Причина возникновения знаков достаточно очевидна: большинство объектов познания и деятельности не доступны непосредственному восприятию в процессе познания и предъявлению в процессе коммуникации.
ПРИМЕЧАНИЕ 1. Вместо слова “знак” в схожем смысле употребляются другие понятия: “имя”, “термин”, “обозначение”.
ПРИМЕЧАНИЕ 2. Вместо слова “денотат” в логике употребляют другие (тождественные, синонимические) названия: чаще всего “значение”, “обозначаемое”.
ПРИМЕЧАНИЕ 3. Термин “концепт” имеет синонимы: “смысл”, “смысл знака”.
Согласно Пирсу все знаки делятся на индексные, иконические и символические по характеру отношения между означающим и означаемым.
В символическом знаке означающее и означаемое соотнесены “безотносительно к какой бы то ни было фактической связи” (например, определенное сочетание звуков, букв, фигур, цветов, движений и т.п. поставлено в соответствие некоторому объекту.
Для построения формальных языков важен именно этот тип знаков (см. параграф первой главы об основном тезисе формализации).
Часто бывает, что знак, впервые возникший как иконический, впоследствии становится знаком-символом.
По мере развития математической символики также происходит замена иконических знаков символами. Например, римская цифра V напоминала раскрытую руку (пять пальцев), а современная цифра 5 является символом.
Денотатами далеко не всегда являются реально существующие предметы и совокупности таких предметов. Множество примеров денотатов, не являющихся объектами реальности, содержится в известной сказке Л. Кэрола “Алиса в стране чудес”. В ней же образно сформулирован принцип возникновения таких денотатов:
“Жить-то он жил (Мартовский заяц- прим авт.), а быть-то он не был”. В этой связи и русская присказка “жил да был” вовсе не кажется тавтологией.
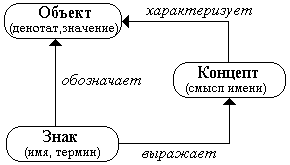
Структура знака описывается так называемым “треугольником Фреге” (по имени выдающегося немецкого логика, много сделавшего для развития теории формальных языков). В другой терминологии он называется “семантическим треугольником” или треугольником Огдена и Ричардса. Он устанавливает связь между знаком, денотатом знака и концептом знака.
Рис. 4.3.1. Треугольник Фреге
С помощью этого треугольника можно прояснить ряд известных языковых эффектов (знаковых ситуаций).
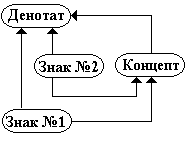
Рис. 4.3.2. Схема синонимии
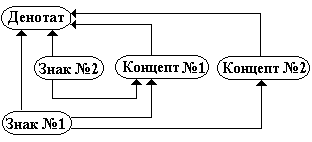
2) знаки могут иметь один и тот же денотат, но обладать разным смыслом (денотативное тождество). Например, знаки “sin 30°” и “1/2” имеют один и тот же денотат, то есть именуют одно и то же действительное число, но смысл этих знаков различен:
Рис. 4.3.3. Схема денотативного тождества
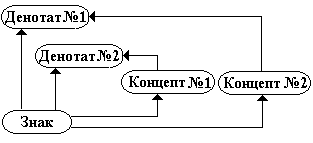
3) Полисемия (многозначность)- наличие у знака более одного значения:
Рис. 4.3.4. Схема полисемии
Дальнейшее развитие языка логики связано с именами Дж.Пеано (1858-1932) и Г.Фреге (1848-1925). Пеано ввел ряд принятых в современной математике символов, в частности “”, “”, “”, для обозначения соответственно отношений принадлежности, объединения и пересечения множеств. Фреге построил аксиоматическое исчисление высказываний и предикатов, в котором содержались все основные элементы современных логических исчислений.
Опираясь на результаты, полученные Фреге, и используя модифицированную символику Пеано, Б.Рассел (1872-1970) и А.Н.Уайтхед (1861-1947) в совместном труде “Принципы математики” (1913) сформулировали основные положения формального языка логики.
В настоящее время язык логики находит важное применение в информатике, при разработке языков программирования, программного обеспечения компьютера, различных технических систем.
Возникновение языков программирования приходится на начало 50-х годов XX века. Первоначально программы создавались на языке машинных команд и представляли собой последовательности двоичных кодов, которые заносились с пульта в компьютер для выполнения.
Для каждого типа машин существовал свой ассемблер, и перенесение программ с машины на машину было очень трудоемкой процедурой. Поэтому возникла идея создания машинно-независимого языка. Такие языки начали появляться с середины 50-х годов, а программа, переводящая предложения этого языка на машинный язык, стала называться транслятором.
Языков программирования и их диалектов (разновидностей) насчитывается несколько тысяч. Классифицировать их можно по-разному. Некоторые авторы разбивают все многообразие языков программирования на процедурные и декларативные. В процедурных языках преобразование данных задается с помощью описания последовательности действий над ними. В декларативных языках преобразование данных задается прежде всего посредством описания отношений между самими данными. Согласно другой классификации, языки программирования можно разделить на процедурные, функциональные, логические, объектно-ориентированные. Однако любая классификация несколько условна, поскольку, как правило, большинство языков программирования включает в себя возможности языков разных типов.