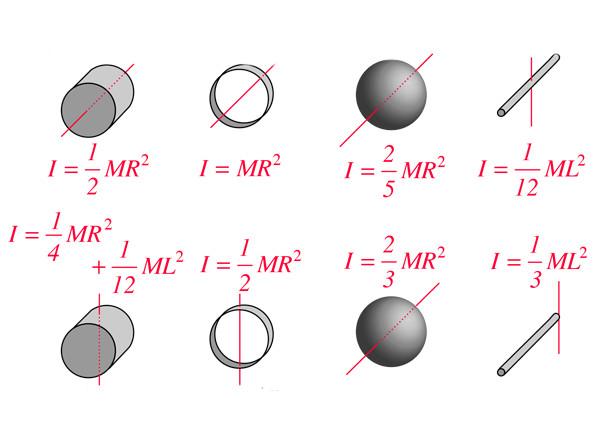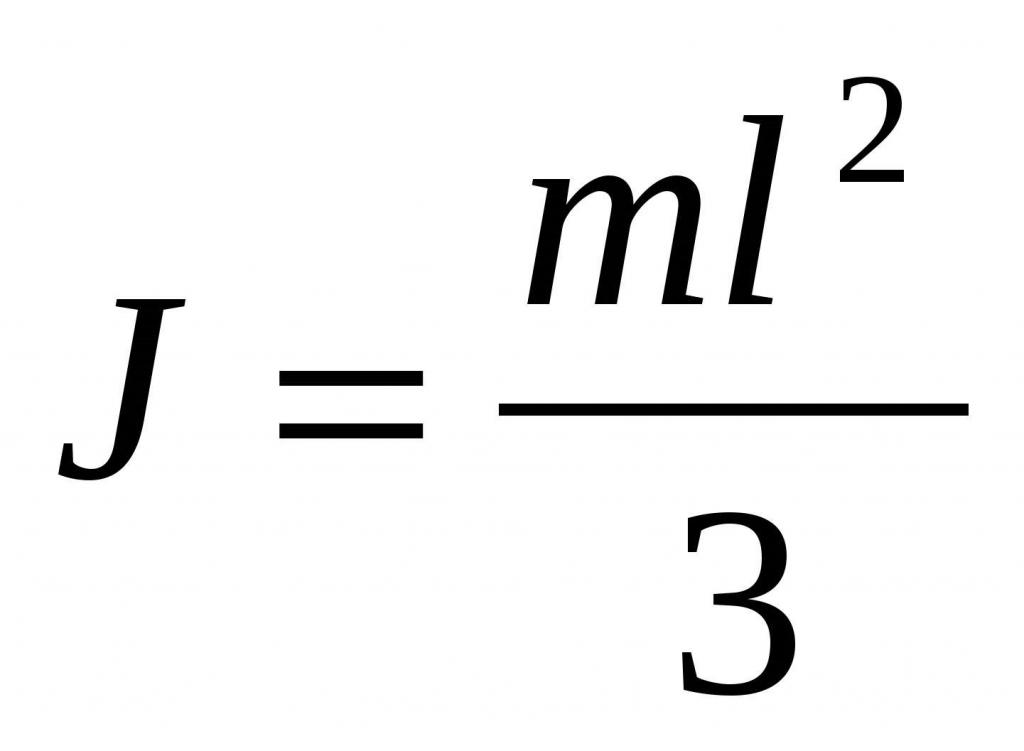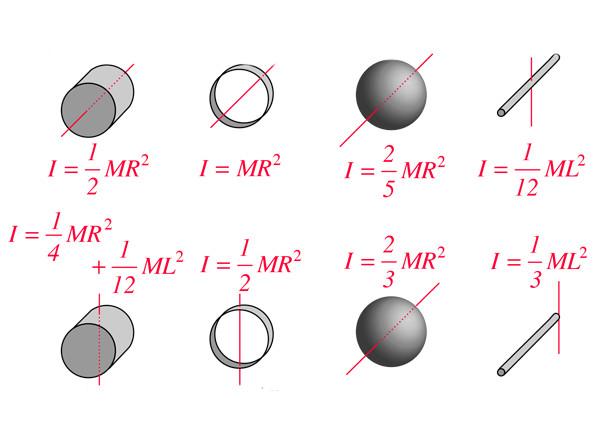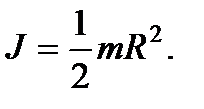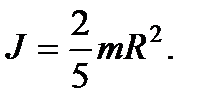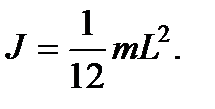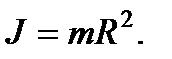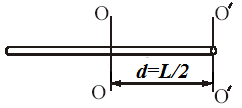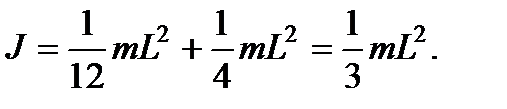Для чего нужен момент инерции в физике
Что такое момент инерции? В чем измеряется момент инерции? Пример задачи
Механика представляет собой один из основных разделов физики, в котором рассматриваются законы движения и равновесия тел. При количественном описании движения вращения важной величиной является момент инерции. В данной статье изучим эту величину. Кроме того, ответим на вопрос о том, в чем измеряется момент инерции твердого тела.
Понятие о моменте инерции для точки материальной
Как физическую величину, его определяют в виде произведения массы на квадрат радиуса вращения. Предположим, что существует некоторая материальная точка, которая имеет массу m. Она вращается вокруг оси, при этом радиус окружности равен r. При заданных условиях инерции, момент вычисляется в соответствии со следующей формулой:

Этой формулой можно пользоваться даже в случаях изучения тел со сложной формой. Главным условием справедливости равенства является наличие огромной разницы между расстоянием до оси вращения r и геометрическими размерами самого тела. Например, при расчете величины I для нашей планеты, которая вращается вокруг Солнца по круговой траектории, можно считать Землю материальной точкой, поскольку расстояние до звезды на несколько порядков превышает радиус планеты.
Величина I для тела произвольной формы
В случае, если геометрические размеры вращающегося тела незначительно отличаются от радиуса r, тогда следует принимать во внимание форму тела. С учетом названного фактора рассчитывают момент инерции с использованием следующей формулы:
По сути, это равенство является суммой моментов инерций всех материальных точек, которые образуют тело. При проведении практических вычислений, записанной формулой пользуются в несколько ином виде, который представлен ниже:
Как видно, интегрирование по массе m заменяется на интегрирование по объему V. Здесь греческой буквой ρ обозначена плотность. Если тело является однородным, то ρ будет постоянной величиной, которую можно вынести за знак интеграла. Если же масса неоднородно распределена по телу, то плотность будет функцией параметра r. Записанную формулу удобно использовать при определении I разных тел, потому что расчет выполняется с помощью мысленного деления тела на элементарные объемы dV.
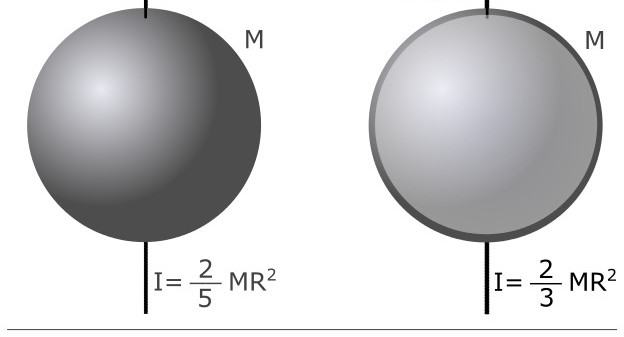
Результаты применения записанного выше равенства для геометрических тел идеальной формы, например, для сферы, цилиндра или стержня, собраны в соответствующие таблицы. В чем измеряется момент инерции? Ниже на рисунке приводятся величины I для некоторых тел. Как видим, все формулы линейно зависят от массы тел и от квадрата геометрического параметра.
В чем измеряется момент инерции тела?
Получив необходимые теоретические сведения для величины I, каждый легко сможет ответить на поставленный вопрос. Действительно, если взглянуть на формулу для I материальной точки, то, отвечая на вопрос о том, в чем измеряется момент осевой инерции, следует ответить, что в килограммах на квадратный метр. Сокращенно эта единица записывается кг*м2. Очевидно, что ту же самую единицу мы получим, если воспользуемся интегральным выражением через объем и плотность.
Отметим, что кг*м2 также можно записать, как м2*кг. Такая форма записи тоже допускается, однако, в практической физике ее не используют.
Поскольку и килограмм, и метр являются системными единицами измерения массы и длины, соответственно, то кг*м2 является также единицей СИ для момента инерции.
Не следует изучаемую единицу путать с другой, которая обозначается, как кг/м2. Хотя ее используют редко, и она не является единицей СИ, тем не менее она позволяет рассчитать соответствующее давление, если ее умножить на ускорение свободного падения.
Пример задачи
Разобравшись, в чем измеряется момент инерции, и как его вычислять, решим следующую задачу: необходимо определить момент инерции Земли, полагая ее материальной точкой.
Для успешного решения этой задачи следует знать всего два параметра: массу планеты и средний радиус ее солнечной орбиты. Оба значения можно посмотреть в соответствующих справочниках. Масса M и радиус орбиты R Земли равны:
Воспользовавшись выражением для вычисления инерции момента точки материальной, приходим к следующему результату:
I = M*R2 = 5,972*1024*(149,6*109)2 = 1,34*1047 кг*м2.
Мы получили гигантское значение. Если сравнить его с моментом инерции Земли относительно ее собственной оси, то окажется, что он будет в миллиард раз меньше рассчитанной величины. Таким образом, приближение материальной точки вполне уместно для рассмотренной задачи.
Момент инерции: формула. Момент инерции тела
Чтобы изменить скорость перемещения тела в пространстве, необходимо приложить некоторое усилие. Этот факт относится ко всем видам механического движения и связан с наличием инерционных свойств у объектов, имеющих массу. В данной статье рассматривается вращение тел и дается понятие об их моменте инерции.
Что такое вращение с точки зрения физики?
Ответ на этот вопрос может дать каждый человек, поскольку этот физический процесс ничем не отличается от его понятия в обиходе. Процесс вращения представляет собой перемещение объекта, обладающего конечной массой, по круговой траектории вокруг некоторой воображаемой оси. Можно привести следующие примеры вращения:
Какие физические величины характеризуют процесс вращения?
Перемещение по окружности описывается набором величин в физике, основные из которых перечислены ниже:
Перечисленные величины связаны друг с другом следующими формулами вращательного движения:
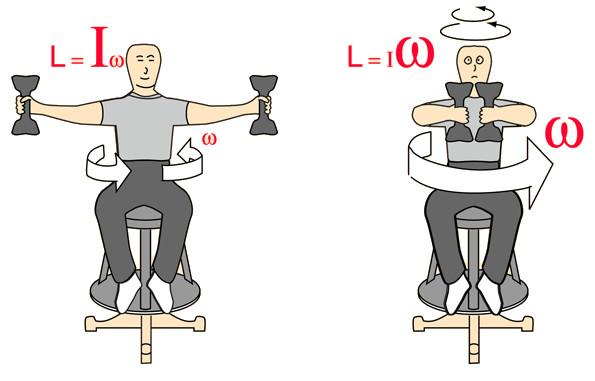
Первая формула описывает круговое движение тела в отсутствие действия внешних моментов сил. В приведенном виде она отражает закон сохранения момента импульса L. Второе выражение описывает случай ускорения или замедления вращения тела в результате действия момента силы M. Оба выражения часто используются при решении задач динамики по круговой траектории.
Как видно из этих формул, момент инерции относительно оси (I) в них используется в качестве некоторого коэффициента. Рассмотрим подробнее эту величину.
Откуда появляется величина I?
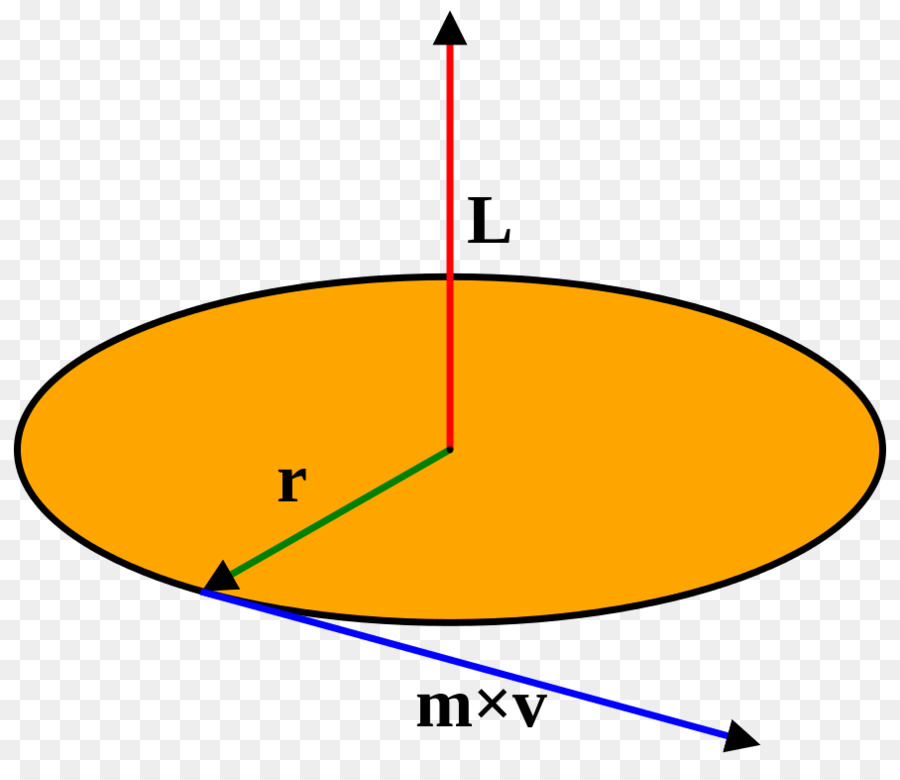
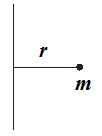
В этом пункте рассмотрим самый простой пример вращения: круговое перемещение материальной точки массой m, дистанция которой от оси вращения составляет r. Эта ситуация приведена на рисунке.
Согласно определению, момент импульса L записывается, как произведение плеча r на линейный импульс p точки:
Учитывая, что линейная и угловая скорость связаны друг с другом через расстояние r, это равенство можно переписать так:
Произведение массы материальной точки на квадрат расстояния до оси вращения принято называть моментом инерции. Формула выше перепишется в таком случае следующим образом:
То есть мы получили выражение, которое было приведено в предыдущем пункте, и ввели в использование величину I.
Общая формула для величины I тела
Если тело разбито таким образом, что i->∞, тогда приведенная сумма заменяется интегралом по массе тела m:
Этот интеграл эквивалентен другому интегралу по объему тела V, поскольку dV=ρ*dm:
Все три формулы используются для вычисления момента инерции тела. При этом в случае дискретного распределения масс в системе предпочтительнее пользоваться 1-м выражением. При непрерывном распределении массы применяют 3-е выражение.
Свойства величины I и ее физический смысл
Описанная процедура получения общего выражения для I позволяет сделать некоторые выводы о свойствах этой физической величины:
Значение I некоторых тел для оси вращения, проходящей через центр масс
Если применить интегрирование по объему для любых тел с произвольным распределением массы, то можно получить для них величину I. В случае однородных объектов, которые имеют идеальную геометрическую форму, эта задача уже решена. Ниже приводятся формулы момента инерции для стержня, диска и шара массой m, в которых составляющее их вещество распределено равномерно:
Далее приведем два примера решения задач на применение общей формулы для расчета I и на использование свойства аддитивности этой величины.
Задача на расчет значения I для системы с дискретным распределением массы
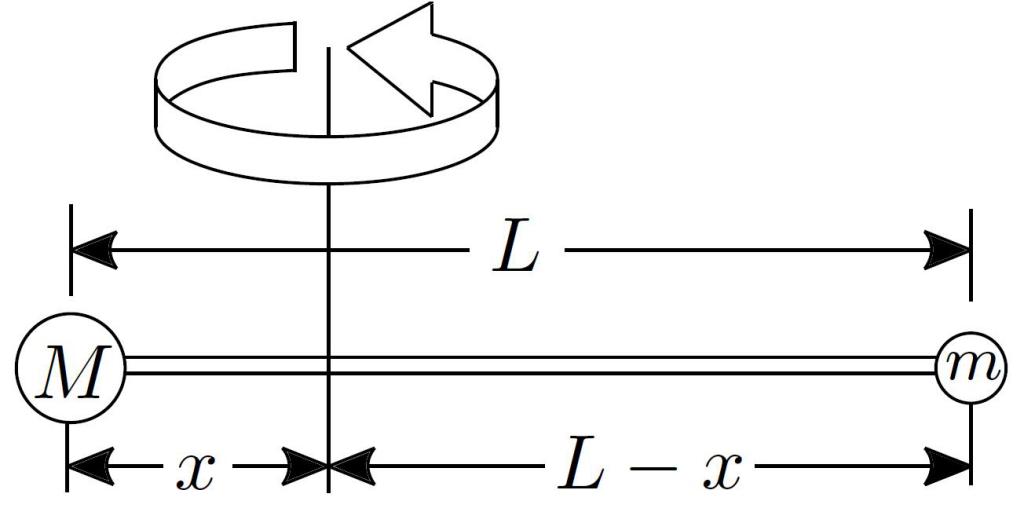
Представим себе стержень длиною 0,5 метра, который сделан из твердого и легкого материала. Этот стержень закреплен на оси таким образом, что она проходит перпендикулярно ему точно посередине. На этот стержень подвешены 3-и груза следующим образом: с одной стороны оси имеются два груза массами 2 кг и 3 кг, находящиеся на расстояниях 10 см и 20 см от его конца, соответственно; с другой стороны подвешен один груз массой 1,5 кг к концу стержня. Для этой системы необходимо рассчитать момент инерции I и определить, с какой скоростью ω стержень будет вращаться, если к одному из его концов приложить силу 50 Н в течение 10 секунд.
Обратим внимание, что при выполнении вычислений все единицы измерения были переведены в систему СИ.
Чтобы определить угловую скорость вращения стержня после действия силы, следует применить формулу с моментом силы, которая была приведена во втором пункте статьи:
Учитывая, что r = 0,25 м, подставляем числа в формулу, получаем:
Полученная величина является достаточно большой. Чтобы получить привычную частоту вращения, следует поделить Δω на 2*pi радиан:
Таким образом, приложенная сила F к концу стержня с грузами за 10 секунд раскрутит его до частоты 136 оборотов в секунду.
Расчет значения I для стержня, когда ось проходит через его конец
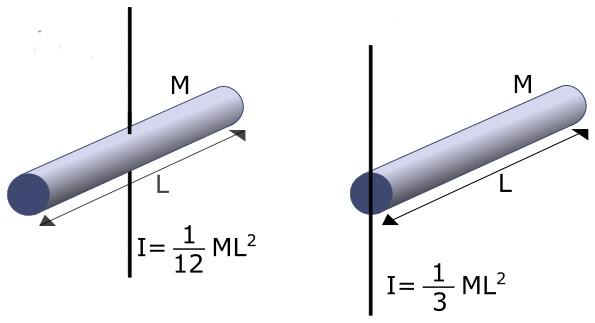
Пусть имеется однородный стержень массой m и длиной L. Необходимо определить момент инерции, если ось вращения расположена на конце стержня перпендикулярно ему.
Воспользуемся общим выражением для I:
Этот интеграл вычислить достаточно просто, получаем:
Любопытно отметить, что момент инерции для того же стержня, когда ось проходит через его центр масс, в 4 раза меньше полученной величины (m*L 2 /3/(m*L 2 /12)=4).
Момент инерции материальной точки и твердого тела: формулы, теорема Штейнера, пример решения задачи
Количественное изучение динамики и кинематики вращательного движения предполагает знание момента инерции материальной точки и твердого тела относительно оси вращения. Рассмотрим в статье, о каком параметре идет речь, а также приведем формулу для его определения.
Общие сведения о физической величине
Сначала дадим определение момента инерции материальной точки и твердого тела, а затем покажем, как его следует использовать при решении практических задач.
Под указанной физической характеристикой для точки, имеющей массу m, которая вокруг оси вращается на расстоянии r, подразумевается следующая величина:
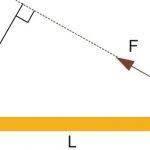
Откуда следует, что единицей измерения изучаемого параметра являются килограммы на квадратный метр (кг*м²).
Если вместо точки вокруг оси вращается тело сложной формы, которое имеет произвольное распределение массы внутри себя, то его момент инерции определяется так:
I = ∫m(r² * dm) = ρ * ∫V(r² * dV).
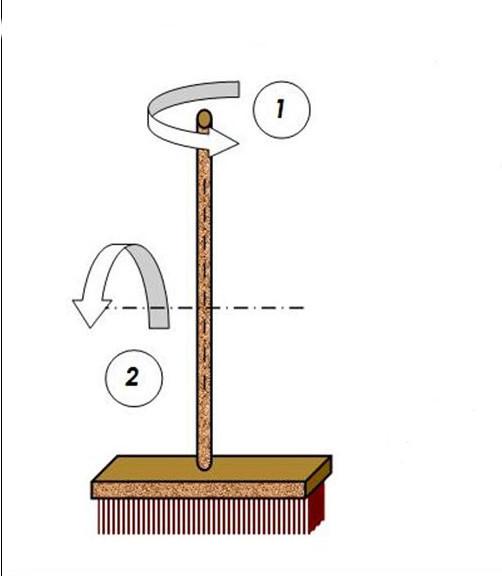
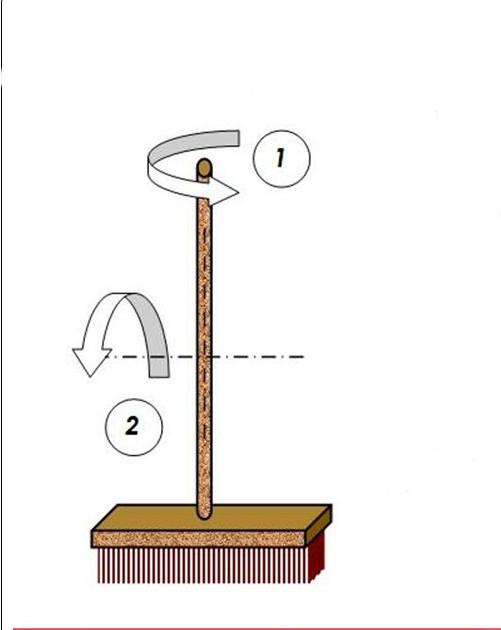
Момент инерции имеет точно такой же смысл для вращения, как масса для поступательного движения. Например, каждый знает, что швабру для мытья полов легче всего вращать вокруг оси, проходящей через ее ручку, чем через перпендикулярную ей. Связано это с тем, что момент инерции в первом случае гораздо меньше, чем во втором.
Величина I для тел разной формы
При решении задач по физике на вращение часто необходимо знать момент инерции для тела конкретной геометрической формы, например, для цилиндра, шара или стержня. Если применить записанную выше формулу для I, то несложно получить соответствующее выражение для всех отмеченных тел. Ниже приведены формулы для некоторых из них:
стержень: I = 1 / 12 * M * L²;
цилиндр: I = 1 / 2 * M * R²;
сфера: I = 2 / 5 * M * R².
Здесь приведены I для оси вращения, которая проходит через центр массы тела. В случае цилиндра ось параллельна генератрисе фигуры. Момент инерции для других геометрических тел и вариантов расположения осей вращения можно найти в соответствующих таблицах. Заметим, что для определения I разных фигур достаточно знать всего один геометрический параметр и массу тела.
Теорема Штейнера и формула
Момент инерции можно определить, если ось вращения расположена на некотором расстоянии от тела. Для этого следует знать длину этого отрезка и величину IO тела относительно проходящей через центр его массы оси, которая должна быть параллельна рассматриваемой. Устанавливающая связь между параметром IO и неизвестным значением I закрепляется в теореме Штейнера. Момент инерции материальной точки и твердого тела математически записывается следующим образом:
Теорема Штейнера значительно облегчает определение I для многих практических ситуаций. Например, если необходимо найти I для стержня длиной L и массой M относительно оси, которая проходит через его конец, то применение теоремы Штейнера позволяет записать:
I = IO + M * (L / 2)2 = 1 / 12 * M * L2 + M * L2 / 4 = M * L2 / 3.
Можно обратится к соответствующей таблице и увидеть, что в ней приводится именно эта формула для тонкого стержня с осью вращения на его конце.
Уравнение моментов
В физике вращения существует формула, которая называется уравнением моментов. Выглядит она следующим образом:
Уравнение моментов по своему смыслу полностью соответствует второму закону Ньютона. При этом I играет роль инерционной массы.
Пример решения задачи
Вообразим себе систему, которая представляет собой цилиндр, закрепленный на вертикальной оси с помощью невесомого горизонтального стержня. Известно, что ось вращения и главная ось цилиндра параллельны друг другу, и расстояние между ними равно 30 см. Масса цилиндра составляет 1 кг, а его радиус равен 5 см. На фигуру действует касательная к траектории вращения сила в 10 Н, вектор которой проходит через главную ось цилиндра. Необходимо определить угловое ускорение фигуры, которое будет вызывать эта сила.
Для начала вычислим момент инерции I цилиндра. Для этого следует применить теорему Штейнера, имеем:
I = IO + M *d² = 1 / 2 * M * R² + M * d² = 1 / 2 * 1 * 0,05² + 1 * 0,3² = 0,09125 кг*м².
Прежде чем пользоваться уравнением моментов, необходимо определить момент силы M. В данном случае имеем:
M = F * d = 10 * 0,3 = 3 Н*м.
Теперь можно определить ускорение:
α = M/I = 3/0,09125 ≈ 32,9 рад/с².
Рассчитанное угловое ускорение говорит о том, что каждую секунду скорость цилиндра будет увеличиваться на 5,2 оборота в секунду.
Момент инерции



Рассмотрим материальную точку массой m, которая находится на расстоянии r, от неподвижной оси (рис. 26). Моментом инерции J материальной точки относительно оси называется скалярная физическая величина, равная произведению массы m на квадрат расстояния r до этой оси:
Момент инерции системы N материальных точек будет равен сумме моментов инерции отдельных точек:
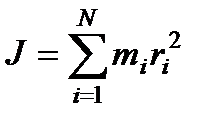
Рис. 26.
К определению момента инерции точки.
Если масса распределена в пространстве непрерывно, то суммирование заменяется интегрированием. Тело разбивается на элементарные объемы dv, каждый из которых обладает массой dm.
В результате получается следующее выражение:
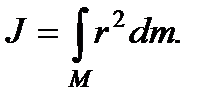
Для однородного по объему тела плотность ρ постоянна, и записав элементарную массу в виде:
dm = ρdv, преобразуем формулу (70) следующим образом:
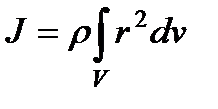
Момент инерции тела является мерой инертности тела во вращательном движении, подобно тому, как масса тела является мерой его инертности при поступательном движении.
Момент инерции — это мера инертных свойств твердого тела при вращательном движении, зависящая от распределения массы относительно оси вращения. Иными словами, момент инерции зависит от массы, формы, размеров тела и положения оси вращения.
Всякое тело, независимо от того, вращается оно или покоится, обладает моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от того, движется оно или находиться в покое. Аналогично массе момент инерции является величиной аддитивной.
В некоторых случаях теоретический расчёт момента инерции достаточно прост. Ниже приведены моменты инерции некоторых сплошных тел правильной геометрической формы относительно оси, проходящей через центр тяжести.
Момент инерции бесконечно плоского диска радиуса R относительно оси, перпендикулярной плоскости диска:
Момент инерции шара радиуса R:
Момент инерции стержня длиной L относительно оси, проходящей через середину стержня перпендикулярно ему:
Момент инерции бесконечно тонкого обруча радиуса R относительно оси, перпендикулярной его плоскости:
Момент инерции тела относительно произвольной оси рассчитывается с помощью теоремы Штейнера:
Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояния между осями.
Рассчитаем при помощи теоремы Штейнера момент инерции стержня длиной L относительно оси, проходящей через конец перпендикулярно ему (рис. 27).
К расчету момента инерции стержня
Очевидно: момент инерции неодинаков относительно разных осей, и поэтому, решая задачи на динамику вращательного движения, момент инерции тела относительно интересующей нас оси каждый раз приходится искать отдельно. Так, например, при конструировании технических устройств, содержащих вращающиеся детали (на железнодорожном транспорте, в самолетостроении, электротехнике и т. д.), требуется знание величин моментов инерции этих деталей. При сложной форме тела теоретический расчет его момента инерции может оказаться трудно выполнимым. В этих случаях предпочитают измерить момент инерции нестандартной детали опытным путем.
Момент инерции
Единица измерения в Международной системе единиц (СИ): кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
В физике, при рассмотрении нескольких систем отсчёта (СО), возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух системах отсчета (далее СО).
Силовая линия, или интегральная кривая, — это кривая, касательная к которой в любой точке совпадает по направлению с вектором, являющимся элементом векторного поля в этой же точке. Применяется для визуализации векторных полей, которые сложно наглядно изобразить каким-либо другим образом. Иногда (не всегда) на этих кривых ставятся стрелочки, показывающие направление вектора вдоль кривой. Для обозначения векторов физического поля, образующих силовые линии, обычно используется термин «напряжённость.
Эта статья о физическом понятии. О более общем значении термина, см. статью СкалярСкалярная величина (от лат. scalaris — ступенчатый) в физике — величина, каждое значение которой может быть выражено одним действительным числом. То есть скалярная величина определяется только значением, в отличие от вектора, который кроме значения имеет направление. К скалярным величинам относятся длина, площадь, время, температура и т. д.Скалярная величина, или скаляр согласно математическому энциклопедическому словарю.
Механи́ческим движе́нием тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.