Для чего нужен сумматор
Сумматор
Сумматор — устройство, преобразующее информационные сигналы (аналоговые или цифровые) в сигнал, эквивалентный сумме этих сигналов. [1]
Содержание
История
Классификация сумматоров
В зависимости от формы представления информации различают сумматоры аналоговые и цифровые. [1]
По способу реализации
По принципу действия
По архитектуре
По способу действия
По способу организации переноса
Двоичный сумматор
Двоичный сумматор может быть определён тремя способами:
1. табличным, в виде таблицы истинности,
2. аналитическим, в виде формулы (СДНФ),
3. графическим, в виде логической схемы.
Так как формулы и схемы могут преобразовываться, то, одной таблице истинности двоичного сумматора могут соответствовать множества различных формул и схем. Поэтому, табличный способ определения двоичного сумматора является основным.
| x0=A | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| x1=B | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | ||
| x2=Pi-1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | Название действия (функции) | Номер функции |
| Si | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | Бит суммы по модулю 2 | F3,150 |
| Pi | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | Бит переноса | F3,232 |
СДНФ суммы по модулю 2:
СДНФ бита переноса:
Cхема, которая обеспечивает сложение двух однобитных чисел А и В называется полусумматором. Полусумматор имеет 4 сигнальных линии: два входа для сигналов, представляющих одноразрядные двоичные числа А и В, и два выхода: сумма А и В по модулю 2 (S) и сигнал переноса (P). При этом S наименее значимый бит, а P наиболее значимый бит.
Схема полного сумматора может быть использована в качестве «строительных блоков» для построения схем многоразрядных сумматоров, путём добавления одноразрядных полных сумматоров. Для каждой цифры, которую схема должна быть в состоянии обрабатывать, используется один полный сумматор.
Двоичный одноразрядный полный сумматор является полной тринарной (трёхоперандной) двоичной логической функцией с бинарным (двухразрядным) выходом. Все три операнда и оба выходных разряда однобитные.
Может быть построен как тринарная (трёхоперандная) двоичная логическая функция с бинарным выходом [5] с временем выполнения операции сложения 2dt, но, для уменьшения аппаратных затрат, обычно строится трёхступенчатым, состоящим из трёх узлов: двух полусумматоров, которые являются полными бинарными (двухоперандными) двоичными логическими функциями с унарным выходом и логического элемента «2ИЛИ».
Троичный сумматор
Так как возможно несколько видов физической реализации троичных систем: трёхуровневая однопроводная, двухуровневая двухразрядная двухпроводная, двухуровневая трёхразрядная одноединичная трёхпроводная, двухуровневая трёхразрядная однонулевая и др., то возможны и несколько видов троичных сумматоров.
Троичный одноразрядный полный сумматор в троичной несимметричной системе счисления является неполной тринарной (трёхоперандной) троичной логической функцией. Два операнда — два слагаемых — полные, третий операнд — троичный разряд переноса — неполный и имеет только два значения 0 и 1 из трёх.
В несимметричной троичной системе счисления
| x0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | слагаемое |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | слагаемое |
| x2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Перенос из n-1 разряда |
| S | 2 | 1 | 0 | 1 | 0 | 2 | 0 | 2 | 1 | 1 | 0 | 2 | 0 | 2 | 1 | 2 | 1 | 0 | МЗР суммы, сумма по модулю 3 |
| C | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | СЗР суммы, перенос в n+1 разряд |
В симметричной троичной системе счисления
| x0 | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | слагаемое | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1 | 1 | 1 | 1 | 0 | 0 | 0 | 7 | 7 | 7 | 1 | 1 | 1 | 0 | 0 | 0 | 7 | 7 | 7 | 1 | 1 | 1 | 0 | 0 | 0 | 7 | 7 | 7 | слагаемое | |
| x2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | Перенос из n-1 разряда | Номер функции |
| S | 0 | 7 | 1 | 7 | 1 | 0 | 1 | 0 | 7 | 7 | 1 | 0 | 1 | 0 | 7 | 0 | 7 | 1 | 1 | 0 | 7 | 0 | 7 | 1 | 7 | 1 | 0 | МЗР суммы | F3,-624603703776 |
| C | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 7 | 7 | СЗР суммы (трит переноса в n+1 разряд) | F3,3483426737048 |
Троичный зеркально-симметричный одноразрядный полный сумматор описан в [10]
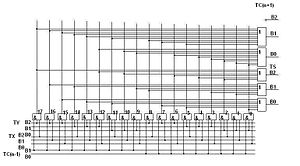
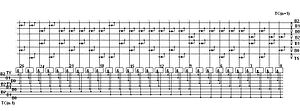
Принципиальная схема одноразрядного сумматора в несимметричной троичной системе счисления в трёхбитной одноединичной системе троичных логических элементов
Принципиальная схема троичного одноразрядного сумматора в двухбитной системе троичных логических элементов
Принципиальная схема троичного полного одноразрядного сумматора, работающего в троичной симметричной системе счисления Фибоначчи в трёхбитной одноединичной системе троичных логических элементов
Принципиальная схема троичного полного сумматора в троичной симметричной системе счисления Фибоначчи в двухбитной системе троичных логических элементов
См. также
Примечания
Литература
Ссылки
Полезное
Смотреть что такое «Сумматор» в других словарях:
Сумматор — в нейронных сетях блок, суммирующий сигналы, поступающие от нейронов через синапсы. В общем случае сумматор может преобразовывать сигналы и передавать их нейронам или сумматорам тоже через синапсы. См. также: Нейронные сети Финансовый словарь… … Финансовый словарь
сумматор — регистр, накопитель, тотализатор, суммирующее устройство; интегросумматор Словарь русских синонимов. сумматор сущ., кол во синонимов: 1 • интегросумматор (1) … Словарь синонимов
СУММАТОР — узел арифметического устройства ЭВМ, осуществляющий операцию суммирования чисел. Выполняется на логических элементах, интегральных схемах … Большой Энциклопедический словарь
СУММАТОР — (1) аналоговый устройство аналоговых вычислительных (см.) для преобразования информационных сигналов различных физ. процессов в суммы нескольких физ. величин. В зависимости от физ. природы входных и выходных величин суммирующие устройства делятся … Большая политехническая энциклопедия
сумматор — 3.1.28 сумматор: Элемент кабельной распределительной сети, обеспечивающий сложение энергии радиосигналов (оптических сигналов) на общей нагрузке. Источник … Словарь-справочник терминов нормативно-технической документации
СУММАТОР — а; м. Основной узел арифметического устройства цифровой вычислительной машины или отдельный прибор, выполняющий операцию сложения двух чисел. Стрелка сумматора. * * * СУММАТОР СУММАТОР, узел арифметического устройства ЭВМ, осуществляющий операцию … Энциклопедический словарь
сумматор — sudėtuvas statusas T sritis automatika atitikmenys: angl. adder; combining unit; summation instrument; summator; summer vok. Addiereinrichtung, f; Addierer, m; Addierwerk, n; Summator, m; Summierer, m; Summierungseinrichtung, f rus. сумматор, m;… … Automatikos terminų žodynas
Сумматор — (от позднелат. surnmo складываю, от лат. summa сумма, итог) основной узел арифметического устройства (См. Арифметическое устройство) ЦВМ, посредством которого осуществляется операция сложения чисел. При поразрядном сложении десятичных… … Большая советская энциклопедия
Сумматор — м. Один из элементов ЭВМ, выполняющий суммирование. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Сумматоры и цифровые компараторы: принцип работы, схемы
 Что такое сумматоры?
Что такое сумматоры?
Сумматоры — это комбинационные устройства, предназначенные для сложения чисел. Рассмотрим сложение двух одноразрядных двоичных чисел, для чего составим таблицу сложения (таблицу истинности), в которой отразим значения входных чисел А и В, значение результата суммирования S и значение переноса в старший разряд P (см. рис. 3.48).
Цифровые сумматоры
Работа устройства, реализующего таблицу истинность (рис. 3.48), описывается следующими уравнениями
Очевидно, что по отношении: к столбцу S реализуется логическая функция «исключающее ИЛИ», т. е. S = А + В.
Поскольку полусумматор имеет только два входа, он может использоваться для суммирования лишь в младшем разряде.
При суммировании двух многоразрядных чисел для каждого разряда (кроме младшего) необходимо использовать устройство, имеющее дополнительный вход переноса. Такое устройство (рис. 3.50) называют полным сумматором и его можно представить как объединение двух полусумматоров (Рвх — дополнительный вход переноса).
Цифровые компараторы
Цифровые компараторы выполняют сравнение двух чисел, заданных в двоичном коде. Они могут определять равенство двух двоичных чисел A и B с одинаковым количеством разрядов либо вид неравенства A> B или A Задать вопрос
Из анализа схемы следует, что если A= B, то F = 1, в противном случае, т. е. при А ≠ В, F = 0. Если А > В, т. е. А = 1, В = 0, то С = 1, а если А В обеспечивается (для четырехразрядного числа) в четырех случаях: или А4 > В4, или А4 = В4 и А3 > В3, или А4 = В4, А3 = В3 и А2 > В2, или А4 = В4, А3 = В3, А2 = В2 и A1 > В1 (где А4 и В4 — старшие разряды чисел А и В). Очевидно, что если поменять местами А1 и B1, то будет выполняться неравенство А В, что позволяет наращивать разрядность обоих чисел. Для этого компараторы соединяют каскадно или параллельно (пирамидально).
Сумматор на ОУ
Что такое сумматор
В общем смысле слова, сумматор — это какое-либо устройство, которое что-либо суммирует и выдает на выходе сумму этих воздействий. Сумматор можно представить в виде какого-либо неизвестного нам ящика, на который поступает входные воздействия и на выходе такого ящика выдается их сумма.
В электронике сумматоры делятся на две группы:
В этой статье мы будем разбирать аналоговые сумматоры.
Аналоговый сумматор
Если, допустим, цена нашего квадратика 1 В, то на данной картинке мы видим постоянное напряжение амплитудой в 1 В. Суммировать постоянное напряжение — одно удовольствие. Для этого достаточно сложить амплитуды этих сигналов в любой момент времени.
На рисунке ниже мы видим два сигнала A и B и сумму этих сигналов: A+B. Если сигнал A = 2 В, сигнал B = 1 В, то сумма этих сигналов составит 3 В.
Все то же самое касается и сигналов с отрицательной полярностью
Как вы видите, при сложении сигналов с равной амплитудой, но разной полярности, мы в сумме получаем 0. То есть эти два сигнала взаимно себя скомпенсировали: 1 +(-1)=0. Все становится намного веселее, если мы начинаем складывать сигналы, которые меняются во времени, то есть переменные сигналы. Они могут быть как периодические, так и непериодические.
Давайте для начала рассмотрим самый простой пример. Пусть у нас будут два синусоидальных сигнала с одинаковыми амплитудами, частотами и фазами. Подадим их на сумматор. Что получится в итоге?
А давайте сместим фазу одного из сигналов на 180 градусов, относительно другого, но при этом амплитуды и частоты сигналов оставим без изменения. Про такие сигналы говорят, что они находятся в противофазе. Как думаете, чему будет равняться их сумма? Долго не думая, смещаем второй сигнал на 180 градусов и суммируем их амплитуды в каждый момент времени. Нетрудно догадаться, что их сумма будет равняться нулю, что мы и видим на рисунке ниже.
Сложение двух сигналов в программном симуляторе
Но что, если нам надо сложить в теории два каких-нибудь два сложных сигнала с разными фазами, амплитудами, частотами? Здесь проще всего прибегнуть как различным симуляторам. Один из них — это Proteus. С помощью него я могу сложить два любых сигнала и посмотреть их сумму. Для этого выбираю синусоидальный генератор
Щелкаю два раза на генератор и задаю его параметры
Давайте сложим два наших синусоидальных сигнала с одинаковыми амплитудами, фазами и частотами, как во втором примере
Прописываем амплитуду и частоту каждого сигнала, остальное ничего не трогаем. Потом нажимаем «пуск»
Потом нажимаем правой кнопкой мыши на наш виртуальный осциллограф и нажимаем Digital Oscilloscope
Сигнал с канала B я немного сдвинул вниз, иначе он совпадает с сигналом А. Оно и неудивительно, так как это два идентичных сигнала.
Для того, чтобы найти их сумму, нам достаточно нажать на кнопку A+B
Получаем сумму двух сигналов
В таком виртуальном осциллографе можно складывать любые два сигнала.
Давайте сложим два таких сигнала
Нажимаем A+B и получаем вот такую сумму сигналов
А давайте сдвинем синусоидальный сигнал на 90 градусов по фазе. Имеем
В результате сумма сигналов будет
На моем реальном цифровом осциллографе тоже имеется такая функция
Здесь на примере ниже я суммирую два сигнала: синусоидальный и прямоугольный. Зеленая осциллограмма — это сумма двух этих сигналов.
Сумматор на ОУ
Инвертирующий сумматор
Как мы уже говорили еще в начале статьи: сумматор — это схема, которая суммирует два и более сигналов. Базовая схема сумматора на ОУ выглядит вот так:
Как и у инвертирующего усилителя, в схеме есть одна особенность. В точке E, где соединяются резисторы, находится потенциал виртуальной земли, о котором мы говорили еще в прошлой статье. Еще эту точку называют точкой суммирования сигналов.
Поэтому, сколько бы мы входных сигналов не подавали на такой сумматор, они не будут влиять друг на друга.
Как не трудно догадаться, для сложения двух сигналов
Формула примет вот такой вид:
Откуда в формуле знак «минус»? Так как эта схема сумматора построена на схеме инвертирующего усилителя, то на выходе будет сигнал со знаком «минус».
Как можно просто сложить два сигнала без всякого усиления?
Неинвертирующий сумматор
Базовая схема будет выглядеть вот так:
Формулы для расчета
Поэтому, сумматор для двух сигналов будет выглядеть вот так:
Если взять R5 = R2 = R3, то у нас будет простой сумматор с единичным коэффициентом усиления, который на выходе даст просто сумму двух входных сигналов.
Причем должно выполняться условие:
то есть в нашем случае отношение этих резисторов должно равняться 2.
Компенсационный резистор в схеме сумматора
Для борьбы с током смещения, в схему также добавляется компенсационный резистор.
Для схемы с двумя входными сигналами он вычисляется по простой формуле
Если входов больше, то его значение вычисляется по формуле
Как работает сумматор на ОУ на примере
Симуляция работы инвертирующего сумматора
Давайте рассмотрим работу нашего сумматора на ОУ в симуляторе Proteus.
На вход такого сумматора будет подавать синусоидальные сигналы с амплитудой в 1 В, но с разной частотой. На in1 у нас будет сигнал с частотой в 50 Гц, на in2 сигнал с частотой в 100 Гц и на in3 сигнал с частотой в 150 Гц. Как вы видите, все 3 резистора после сигналов имеют одинаковый номинал в 1 кОм для удобства расчета коэффициента усиления. То есть все сигналы будут усиливаться одинаково. Резистор R2 имеем номинал в 2 кОм. Это значит, что коэффициент усиления на выходе будет равен 2. То есть сумма сигналов будет помножена на коэффициент 2 и инвертирована.
Итак, для того, чтобы посмотреть сигналы как на экране осциллографа, можно также воспользоваться инструментом аналоговым анализатором
на рабочем поле появится окно Analogue Analysis
Для того, чтобы анализировать входы, просто переносим в наше окошко входы in1, in2, in3 и выход out, удерживая левую кнопку мыши
В результате увидим это
Потом нажимаем пробел и в большом окне уже видим все наши сигналы: и входные, и выходной. (нажмите на картинку, откроется в новом окне)
черная осциллограмма — это и есть сумма всех трех синусоид усиленная в 2 раза, но со знаком «минус».
В чистом виде на выходе ОУ у нас будет только черная осциллограмма. Она является суммой всех входных сигналов, помноженная на 2, но со знаком «минус».
Работа неинвертирующего сумматора
Итак, давайте соберем простой нормальный сумматор для, который бы просто складывал сигналы и на выходе выдавал нормальный неинвертированный сигнал. Для того, чтобы создать такой сумматор, наш коэффициент усиления должен быть равен единице, а на выходе мы должны инвертировать такой сигнал. Настало время использовать схему для неинвертирующего сумматора
Итак, все что мы хотим — это просто сложить три сигнала и посмотреть их сумму. И все! Не надо ничего усиливать и инвертировать. Поэтому, наша схема будет выглядеть вот так:
В этой схеме первый каскад на ОУ суммирует входные сигналы, а второй каскад просто инвертирует получившийся сигнал. В каждом усилителе коэффициент передачи равен 1, поэтому, никакого усиления сигнала в данной схеме не происходит.
Итак, осциллограмма со всеми сигналами
Если оставить на экране только осциллограмму выходного сигнала
Тот же самый эффект мы можем получить и с помощью схемы на одном ОУ, о которой я упоминал выше:
Давайте на его входы подадим два одинаковых синусоидальных сигнала, но в противофазе. То есть мы должны получить что-то типа этого
Проверяем симуляцию и видим, что сумма двух одинаковых сигналов в противофазе действительно равняется нулю
АЧХ и ФЧХ сумматора
Все вы помните, что реальный ОУ — это не идеальный радиоэлемент. С ростом частоты его усилительные свойства начинают падать. Для того, чтобы рассмотреть, как ведет себя сумматор на ОУ, давайте построим виртуальную АЧХ для математической модели ОУ LM358, который мы задействуем в схеме сумматора. На два входа мы будем подавать сигнал с одного и то же генератора. То есть в данном случае у нас на входы подаются два абсолютно идентичных сигнала.
Частота единичного усиления уже будет равняться 600 кГц
Если рассмотреть ФЧХ, то можно также заметить, что после 10 кГц начинает меняться фаза сигнала
Поэтому, при разработке всегда учитывайте неидеальность характеристик ОУ, которые также можно посмотреть в даташите.
Сравнение неинвертирующих сумматоров
Давайте сравним схему неинвертирующего сумматора на двух ОУ
и неинвертирующего сумматора на одном ОУ
Для более удобной симуляции мы на них будем подавать и суммировать один и тот же сигнал синусоидальный сигнал
Давайте рассмотрим, что же случится с выходным сигналами на ФЧХ. Как можно увидеть, сигнал неинвертирующего сумматора с двумя ОУ будет запаздывать по фазе больше, чем с одним ОУ. Это объясняется тем, что каждый ОУ вносит небольшую задержку.
Плюсы и минусы инвертирующего и неинвертирующего сумматора
Не забывайте, что инвертирующий сумматор на выходе будет давать сумму сигналов со знаком «минус», умноженных на коэффициент усиления. Неинвертирующий сумматор выдаст на выходе просто сумму сигналов умноженных на коэффициент усиления. Также инвертирующий сумматор проще построить и рассчитать. Если вы создаете какой-либо микшер на основе сумматора, то для человеческого уха нет никакой разницы, инвертируемый сигнал на выходе или нет. Поэтому, в этом случае будет проще применить инвертирующий сумматор.
Применение аналогового сумматора
В настоящее время аналоговый сумматор используется в схемах, где надо суммировать два и более аналоговых сигналов. Это могут быть микшеры звукового диапазона, где надо объединить выходные сигналы от микрофонов, а также от устройств, которые создают различные спецэффекты и которые потом можно добавить к основной звуковой дорожке. Вся прелесть микшеров на ОУ заключается в том, что входные сигналы никак не влияют друг на друга. А также это могут быть схемы операционной обработки сигналов для выполнения арифметической обработки сигналов (сложение/вычитание).
Рекомендую посмотреть классное видео про сумматор:






 Что такое сумматоры?
Что такое сумматоры?




























































