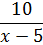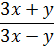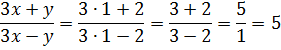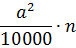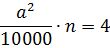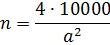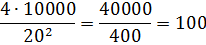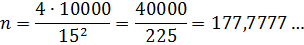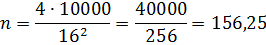Для чего нужна алгебра
Вот зачем нужна школьная алгебра
Обычно на вопрос «зачем нужна математика?» отвечают что-то вроде «гимнастика для ума». На мой взгляд, этого объяснения недостаточно. Когда человек выполняет физические упражнения, то он знает точное название групп мышц, которые при этом развиваются. Но разговоры про математику остаются слишком абстрактными. Какие конкретно «мышцы ума» тренируются школьной алгеброй? Она ведь совсем не похожа на настоящую математику, в которой делаются великие открытия. Что дает умение искать производную каких-то запутанных функций?
Преподавание программирования слабым студентам привело меня к более точному ответу на вопрос «зачем?». В статье я постараюсь донести его вам.
В данном примере от ученика ожидают, что он вспомнит формулу квадрата суммы
В более сложных случаях, полученное выражение можно использовать для других преобразований. Например:
преобразуется сначала в
Чтобы добиться такого результата, ученику нужно распознать в исходном выражении и потом применить три формулы:
Это практически определение рефакторинга из одноименной книги Мартина Фаулера.
В своем труде, автор формулирует их следующим образом:
Рефакторинг (Refactoring) (сущ.): изменение во внутренней структуре программного обеспечения, имеющее целью облегчить понимание его работы и упростить модификацию, не затрагивая наблюдаемого поведения.
Производить рефакторинг (Refactor) (глаг.): изменять структуру программного обеспечения, применяя ряд рефакторингов, не затрагивая его поведения.
В книге даются «формулы», которые нужно распознать в исходном коде и правила их преобразования.
В качестве простейшего примера, приведу «введение поясняющей переменной» из книги:
Части выражения нужно записать в переменную, имя которой поясняет его назначение.
Представьте себе человека, который не может упрощать алгебраические выражения с использованием формулы квадрата суммы и разности квадратов.
Как вы думаете, сможет ли этот человек рефакторить код?
Сможет ли он вообще написать понятный другим людям код, если у него не сформирован идеал этой самой лаконичности? На мой взгляд — нет.
Однако в школе учатся все, а программистами становится меньшинство. Полезен ли навык преобразования выражений для обычных людей? Я думаю да. Только навык применяется в более абстрактном виде: нужно оценить ситуацию и выбрать дальнейшее действие так, чтобы приблизиться к цели. В педагогике этот феномен называется перенос (навыка).
Даже при езде на автомобильном транспорте, водитель постоянно занимается распознаванием шаблонов в окружающем мире и выполнением соответствующих маневров, чтобы добраться до цели.
Когда ты умер, ты об этом не знаешь, только другим тяжело. То же самое, когда ты не освоил математику…
Что же происходит, если человеку не удалось освоить преобразование выражений? Время от времени я веду индивидуальные занятия со студентами, у которых в школе было плохо с математикой. Как правило, они напрочь застревают на теме про циклы. Настолько, что с ними приходится заниматься «алгеброй», но на языке программирования.
Это происходит потому, что при написании циклов основной прием как раз и заключается в том, чтобы преобразовать группу одинаковых выражений.
Допустим результат работы программы должен выглядеть так:
Введение
Глава 1
Глава 2
Глава 3
Глава 4
Глава 5
Глава 6
Глава 7
Заключение
Тривиальная программа для достижения этого результата выглядит так:
Но это решение далеко от лаконичного идеала. Сначала в нем нужно найти повторяющуюся группу действий и потом преобразовать. В итоге получится такое решение:
Если же человек в свое время не освоил математику, то и выполнять подобные преобразования он не сможет. У него просто не будет соответствующего навыка. Именно поэтому тема циклов — первое препятствие в обучении разработчика.
Похожие проблемы возникают и в других областях. Если человек не умеет использовать подручный инструмент, то он не сможет проявлять бытовую смекалку. Злые языки будут говорить, что руки не из того места растут. На дороге это проявляется в неумении правильно оценить ситуацию и выбрать маневр. Что иногда может привести к трагическим последствиям.
Зачем нужна алгебра
Да, и вообще все эти предметы, вроде геометрии, физики, химии, литературы и т.д. Ведь в реальной жизни мало кто пользуется этими знаниями. Кроме, конечно же, строителей, инженеров. писателей и т.д.
А простому обывателю, вроде Васи с соседнего двора, зачем он ему нужен?
Все эти, казалось бы, на первый взгляд, никчемные предметы, оказывается формируют стиль мышления.
Вспомните, кто в школе любил решать алгебраические задачи с несколькими не известными параметрами. Например: Найдите игрик, если икс один равен много букв, икс два мало букв, буква б равна достаточно букв.
Человек, который хорошо занимался алгеброй, начнет сразу же с построения цепочки, затем упростит это выражение и в конце решит задачу.
Т.е. алгебра помогает при обычной жизни следующим образом, на примере хаоса в комнате:
1. Увидеть полный хаос в комнате.
2. Вспомнить что, где и как должно лежать.
3. Разбить хаос на пункту и части.
4. Начать уборку по пунктам и частям.
Т.е. люди, которые любили алгебру. они упрощают задачу до такой степени, чтобы его было возможно легко решить. Кстати, моя жена любит алгебру:)
1. Слышу высказывание
2. Начинаю размышлять, что оно означает
3. Откуда пришло это высказывание? Правдиво ли оно? Если нет, то почему?
4. Как она влияет на это?
5. Почему она влияет на это?
6. Для чего это высказывание?
Таким образом, когда приходится решать какую-либо задачу, например уборка комнаты, я вместо того, чтобы упростить и решить задачу, настолько сильно закручиваю, что жена прям в бешенство впадает. Но за то, после того, как все вопросы сняты, теоремы доказаны (почему носки должны лежать в одной коробке, а трусы в другой), аксиомы приведены (грязное белье лежит отдельно в ванной комнате, а чистое в шкафу), только после этого начинается решение задачи.
Т.е. человеку с геометрическим типом мышления, необходимо все разжевать и предоставить задачу, иначе Вы получите столько теорем и аксиом с решенной задачей, что сами запутаетесь:))) Если конечно, Вы не человек с физическим типом мышления.
Что могу сказать по поводу физиков. Эти ребята жесткие, все делают по правилам. А если правил нет, то создают его на основе других правил. На примере: Грязное белье отдельно, чистое отдельно.
1. Грязное белье отдельно от чистого, т.к. грязное с чистым не совместимы.
2. Если их совместить, то чистое превратится в грязное,и попадет в ваную комнату для стирки.
3. Если много вещей надо стирать, то придется потратить много времени.
4. Время это то чего постоянно не хватает.
5. Создаем промежуточный отдел для носки получистой одежды.
6. Тогда в ванной комнате не накапливается грязная одежда.
7. Если мало грязной одежды, то появляется время на что-то другое.
8. Раз уж появилось время, не сходить ли выпить пивка?
9. Пойду в одежде с промежуточного отдела.
Впрочем, отец на то и отец, что его указы не обсуждаются:)))
Ну, а литература нужна нам, чтобы мы могли культурно общаться между собой!
Зачем нужна математика в жизни человека?
Так ли необходима алгебра?
Удивительное дело, не только у нас появляются желающие отменить математику для тех, кому это не нужно. Скажем, поэтам, журналистам, историкам и прочим гуманитариям математика в таких количествах, да еще такая сложная, да еще та, что сдается обязательно, и не требуется вовсе. Развить логическое мышление можно и как-нибудь иначе. Ну зачем же так мучить детей, которые точно знают, что им все это никогда в жизни не потребуется. Замечательное слово “профилизация’’ очень по сердцу пришлось многим. Меня в этом вопросе умиляют гуманитарии, которые так радостно воспринимают ограничение получаемых знаний. Заметим, однако, что технари так ожесточенно не восстают против изобилия гуманитарных предметов, хоть их и преподают не лучше, чем предметы естественнонаучного цикла, да и не лучше математики.
Итак, недавняя статья в Нью-Йорк Таймс Написал ее политолог Эндрю Хэкер, почетный профессор Квинс-колледжа университета Нью-Йорка. Вот какие аргументы автор приводит против всеобщего изучения математики на приличном уровне.
Видео
Математика развивает мышление
Зачем заниматься физкультурой? Ответ простой — для здоровья и красоты тела.
Зачем учить математику? Ответ на этот вопрос кажется менее очевидным.
Математика — это гимнастика для ума. Хочешь не хочешь, но в процессе изучения будут крепчать качества, которые влияют на способ мышления. Для этого не обязательно учиться в профильном классе и участвовать в олимпиадах — решение даже самых простых задачек на пропорции или с процентами дает значительный эффект.
Обобщение, сокращение, анализ, систематизация, выделение важного, поиск закономерностей, формулирование гипотез и доказательство теорий — все это помогает развить мышление, сделать его более гибким. Точно также, как физические упражнения делают наше тело подвижнее, дают заряд сил и тренируют выносливость, математика тренирует ум.
Математика развивает интеллект. Набор правил и функций, которые мы изучаем в школе, делают наше мышление последовательным и логичным. Это отражается на умении рассуждать, формулировать мысли и замечать взаимосвязи. И самое увлекательное, что эти знания можно (и нужно!) применять не только в школе, но и в нестандартных ситуациях: чтобы выбрать самую выгодную банковскую карту, просчитать литры краски для ремонта или создать карту сокровищ, чтобы не забыть где они спрятаны.
Математика — универсальный международный язык, которым владеют почти все люди на земле. Эти знания пригодятся в любой стране и могут стать предметом интересной беседы.
Необычный способ познакомиться — спросить человека про его отношение к математике, где он ее использует и помнит ли, как извлечь квадратный корень из числа. Да, кому-то это покажется странным, но зато вас точно запомнят. 🤓
Что понять, зачем учить математику в школе, только представьте, как приятно, когда в голове нет «каши» и путаницы в рассуждениях. На этот счет еще в прошлом веке великий учёный Ломоносов сказал: «Математику только затем учить надо, что она ум в порядок приводит». Как тут можно спорить? 😇
Какие науки применяют алгебру
Мы с вами разобрались, что такое алгебра, и чем она может быть полезна. Теперь рассмотрим, какие же науки не обходятся без нее.
Вспомним, что она является не самостоятельной дисциплиной, а всего лишь разделом математики. А математика подразделяется на арифметику (изучается в младших классах общеобразовательной школы) и на геометрию (изучают в средней школе). Почему они взаимосвязаны? Дело в том, что арифметика – это очень простые вычисления: сложение, вычитание, умножение и деление. Это все пригодится в дальнейшем обучении.
Что касается геометрии, то она изучает пространственные структуры. То есть речь идет о различных вычислениях у фигур, линий, в пространственных телах.
Без алгебры не могут существовать:
Даже некоторые гуманитарные науки не обходятся без нее, например социология.
Какие темы относятся к алгебре
Рассмотрим, какие задачи решает алгебра:
Этот раздел математики достаточно сложен. Еще с древних времен известные ученые создавали законы, формулы, теоремы, основываясь на жизненном опыте. Недаром математика считается не просто точной наукой, но и мистической.
Математика тренирует память
Ученые из Стэнфордского университета в США изучили, как человек решает математические задачи и выяснили, что взрослые люди используют для этого навык «доставать» из памяти ответы на основе прошлого опыта.
Почему учителя настаивают на регулярном посещении уроков? Дело не в их вредности, а в том, что при решении математических задач, мы «достаем» из памяти ответы на основе прошлого опыта. А чтобы этот опыт закрепить, нужно повторять материал и тренироваться в решении примеров. Только так можно запомнить все правила и формулы. 🤓
В журнале Nature Neuroscience в 2014 году опубликовали исследование про роль определенных областей головного мозга в развитии познавательной активности детей. Оказалось, что на интерес к знаниям оказывает сильное влияние гиппокамп — часть мозга, которая отвечает за память.
Интересный факт! Определенные области головного мозга влияют на развитие познавательной активности детей. Например, на интерес к знаниям влияет часть мозга, которая отвечает за память — гиппокамп. Поэтому:
Математика — волшебница, не иначе! Систематизируем все волшебные свойства и повторим, какие навыки можно развить с помощью математики:
(заклинание, которое убирает препятствия к знаниям)
Знакомимся с алгеброй!
Ну что, дорогие товарищи! Могу вас поздравить! Мы с вами медленно, но верно взрослеем! И математика, с которой мы с вами будем работать, тоже потихоньку будет становиться серьёзнее, да.)
В чём же будет заключаться наше взросление? А взросление будет заключаться вот в чём.
Все мы с начальной школы уже попривыкли работать с числами. Складывать/вычитать, умножать/делить числа. Самые разные — целые и дробные, положительные и отрицательные. Но! Жизнь — штука многогранная! И преподносит много сюрпризов. И вот один из них.
В жизни очень часто приходится работать с различными числовыми величинами не в конкретном, а в общем виде. Это может быть время, расстояние, температура, цена, скорость — совершенно любая числовая величина. Т.е. величина, которую как-то можно выразить числом (секунд, дециметров, рублей, километров в час и так далее). Взаимоотношения между величинами задаются в математике, чаще всего, формулами. Прямо в общем виде. Или уравнениями. Вспомните хотя бы простенькие задачки на движение, для решения которых используется ключевая формула:
S = V·t
S — пройденный путь,
V — скорость движения,
К сожалению, для работы с числовыми величинами в общем виде, одних только чисел (т.е. набора циферок) уже недостаточно. Требуются ещё и буквы. Которые как раз и характеризуют нужную нам величину в общем виде. Стало быть, для работы с общей (буквенной) записью числовых величин (т.е. формулами и уравнениями) нужна своя математика. И она есть! Как только к чиселкам в употребление добавляются ещё и буковки, то привычная нам арифметика превращается в… Превращается в… грамматику?) Не-а! Не угадали.) В алгебру! Красивое и мощное слово.)
Естественно, в новом разделе математики (алгебре) возникают свои правила и свои порядки. Некоторые вещи будут хорошо знакомы вам из арифметики (сложение/вычитание, умножение/деление, сокращение дробей, возведение в степень и т.д.), но некоторые будут и непривычными. Почему? А потому, что новыми! А любая новизна всегда предполагает некоторый период привыкания, да.) Вот и мы освоимся и попривыкнем.
Что изучает алгебра? Как работает алгебра?
Итак, предмет алгебры. Что же изучает алгебра?
Фактически, алгебра — это просто обобщение изучения арифметики. Ни больше, ни меньше.
Итак, удивляемся, но запоминаем. Буквы в алгебре — это, фактически, те же самые числа! Только числа эти замаскированные. Или подразумевающиеся. И поэтому носят особое название — переменные величины. Или кратко — переменные.
Почему — переменные? А потому, что под любой буквой в алгебре всегда скрывается какое-то число. И любую букву при желании можно заменять на какое-то число. Совершенно любое (какое допустимо, конечно). Об этом в первом уроке про числовые и алгебраические выражения немного говорилось. Но и тут не грех вспомнить будет.)
Например, возьмём конкретное алгебраическое выражение. Пусть а+1. В нём есть единичка (число 1), которая вопросов обычно ни у кого не вызывает. Единичка и в Африке единичка. И ещё есть буковка «а». А вот тут уже у многих появляются вопросы, да… Что это за буква такая? Что она означает и зачем вообще написана?
Ответ: буковка «а» – это и есть та самая переменная величина.
Между прочим, простенькие алгебраические выражения очень легко и просто расшифровываются словесно. Да-да! Великий и могучий русский язык способен очень на многое. В том числе и в математике, да.
Например, словесная расшифровка нашего злого выражения а+1 будет при этом гласить: к любому числу (а) прибавить единичку (1).
Обратите внимание на слова — именно «любому числу» (а не букве!). Не можем мы складывать буквы с числами «в лоб». Как и не можем складывать метры с килограммами, да…
Запоминаем:
Буквы в алгебре — это просто символы! Под которыми скрываются различные числа. И не более того. Буквы можно заменять на различные числа.
Потренируемся теперь в словесной расшифровке более сложных алгебраических выражений. Возьмём другое выражение. Посложнее. Например:
Так прямо по-русски и читаем: десятку (10) поделить на разность любого числа (х) и пятёрки (5).
Конечно, здесь число икс может быть уже не совсем любым. Про смысл алгебраического выражения помните? И чем же у нас не может быть икс в этом выражении? Правильно, пятёркой не может быть! То есть, числом, при подстановке которого получается запретное действие (в данном случае — деление на ноль).
А как словесно расшифровать выражение, скажем, x+y?
Легко! К любому числу икс (х) прибавить любое число игрек (у).
Или так: сумма любых двух чисел икс (х) и игрек (у).
Да-да! Именно так. Только весь фокус этого алгебраического выражения состоит в том, что под буквами икс и игрек скрываются (подразумеваются), в общем случае, уже разные числа. Именно поэтому используются и разные буквы, да.)
Например, если бы мы твёрдо были уверены, что нам надо сложить два одинаковых числа (например, 1+1 или 5+5), то алгебраически мы бы записали:
А вот если нам надо сложить два разных числа (скажем, 1+2 или 5+7) то для этого другого числа нам и букву другую выбирать приходится, да… Такова суровая жизнь.)
Запоминаем:
В алгебре под одинаковыми буквами подразумеваются одинаковые числа. А под разными буквами — в общем случае, разные числа.
Почему я сделал оговорку «в общем случае»? Потому, что в частном случае — да, под разными буквами могут оказаться и одинаковые числа. При желании.) Скажем, в выражении х+у мы же имеем право взять икс и игрек по единичке? Имеем! Сложим — получится двойка. Возьмём икс и игрек по сотке и сложим — получим двести. И так далее…
Но любой частный случай — лишь часть общего. На то он и частный, да.) А в общем случае, данная запись говорит нам о том, что числа икс и игрек — разные. И буквы — тоже разные.
Понимание сути назначения чисел и букв в алгебре позволяет, как минимум, понимать и решать простейшие задания. Например, такое:
Всё проще простого. Если не понимать смысл назначения буковки b в выражении 2b+3, задание не решить, да… Но мы-то ведь уже в теме, правда?)
Итак, мы знаем, что в алгебраическом выражении 2b+3 под буквой b (или переменной b, что одно и то же) скрывается какое-то число. Какое именно — обычно мы не знаем. Но в нашем задании значение b указано конкретно прямым текстом. Это 0,3. Что надо сделать? Правильно, просто тупо подставить вместо b число 0,3 да и посчитать, что получится:
Это правильный ответ.
Если бы в задании было бы сказано: «… при b = 0″, что бы мы делали? Правильно! Подставляли бы вместо b нолик. И снова считали. Получили бы 3. И так далее. Улавливаете?)
Или другое задание. Покруче.
Имеет ли смысл выражение
И снова перед нами алгебраическое выражение. Ибо помимо конкретного постоянного числа (тройки), в нашем выражении тусуются ещё и буковки. Целых две — икс и игрек. Выражение более сложное. Дробь какая-то… Ну и ладно.) Чтобы справиться с заданием, достаточно самых начальных знаний алгебры. Никаких специальных правил действий с алгебраическими дробями здесь знать не нужно. Совсем.) Об этом в других, более серьёзных уроках, будет.)
Итак, мы в курсе, что под буквами икс и игрек тоже скрываются какие-то числа. Различные числа. Поэтому и буквы в задании — разные.)
В качестве конкретных значений этих различных чисел нам предложены двойка (х) и шестёрка (у).
Вот и подставляем двойку и шестёрку вместо икс и игрек в нашу дробь и смотрим, что получится-то…
Чтобы не наляпать ошибок (оно нам надо?), можно по отдельности сосчитать числитель и знаменатель. Вот и действуем.
Ну ладно. Двенадцать так двенадцать. Так уж получилось…
Хорошо, считаем знаменатель:
Ух ты, какая забавная штука-то… А знаменатель-то нулю оказался равен! На который делить нельзя, да… Надеюсь, вы помните из арифметики, что дробь — это деление? Числителя на знаменатель?)
Вот вам и ответ: нет. Выражение не имеет смысла.
Прошу заметить одну важную вещь: наше выражение не имеет смысла не вообще само по себе, а только при предложенных значениях переменных (x=2 и y=6). При каких-нибудь других значениях букв (скажем, при x=1 и у=2) у нашего выражения смысл появляется:
Почувствуйте разницу, как говорится!
И тут я слышу неосторожный вопрос:
А зачем нужна алгебра? Какие задачи она изучает и решает?
И правда, зачем нам вообще городить весь этот огород с числами и буквами, что-то там подставлять, да ещё и периодически посматривать, считабельно или нет?
Зачем нам вся эта символьная и буквенная схоластика… пардон… алгебра?
Вообще-то, со смысла и назначения алгебры наш урок и начинался, но, так уж и быть, отвечаю ещё раз.
Ответ:
Алгебра — мощнейший инструмент для работы с формулами! Для решения уравнений (и неравенств). И особенно — решения задач! Самых разных! Кстати, не только по математике, но и по физике, химии, экономике и другим точным наукам.)
В том числе алгебра нужна и для решения обычных житейских задач. Из реальной повседневной жизни, да.)
И вы в магазине решаете такую житейскую задачку: сколько надо заказать квадратных плиток «n» со стороной «a» см, чтобы облицевать весь пол в ванной и использовать все плитки полностью, ни одну не разрезая?
Для решения этой житейской задачки вполне достаточно обычной школьной алгебры!
Итак, нам известна площадь всей ванной комнаты. Это 4 квадратных метра. Или просто 4. Постоянное число. Также нам известна длина стороны плитки. Это «a» сантиметров. Переменная величина. Ибо длину стороны плиточки мы с вами подбираем. Не знаем мы точного значения… Поэтому вместо циферки вводим буковку, да.) И ещё есть количество этих самых плиточек «n». Тоже буковка, да. Ибо конкретного количества-то плиточек мы тоже не знаем!)
Как составить алгебраическое выражение (формулу) для решения задачи?
Подключаем житейскую логику и здравый смысл. Площадь всей ванной знаем? Знаем! Это 4 (квадратных метра). Площадь комнат в квартире она обычно в квадратных метрах измеряется, да…)
Запоминаем раз и навсегда:
Все однотипные величины в задачах алгебры (в нашем случае это — площадь) должны быть выражены в одинаковых единицах измерения!
Иначе составленное выражение будет неверным, да…
Поэтому площадь одной плиточки в квадратных метрах составит вот такую величину:
А у нас таких плиточек сколько? Конкретно — не знаем. Но в общем виде — знаем! Это n штук. Я же не зря говорил, что буквы в алгебре — это как бы числа. Только не конкретные, а подразумеваемые. Вот и умножаем эту штуковину на n! Всю целиком:
А теперь, чтобы замостить плитками пол в ванной без зазоров и разрезов, должно выполняться железное равенство:
Где 4 — это наши известные четыре квадратных метра площади ванной комнаты.)
А уж выразить буковку n из полученного равенства (формулы) уже не такая большая проблема даже для нашего начального уровня. Хотя бы по правилам работы с дробями и пропорциями:
Вот мы и составили алгебраическое выражение (или более научно — формулу) для подсчёта заказываемых плиточек.
А теперь начинаем наш подбор. Подойдёт ли нам плиточка размером, скажем, a=20 см? И сколько таких плиточек понадобится заказать? Как подсчитать? Подставляем вместо буквы «a» в выражение двадцатку да и считаем:
То есть n = 100. Отлично! Ровно сто плиток нам понадобится!
А если сторона плитки a=15 см? Что ж, опять подставляем и считаем:
Вот-те раз! Число n получилось дробным! Житейски это значит, что покупать надо 178 плиток, но одну из них придётся резать (болгаркой, например). И не факт, что ровнёхонько получится разрезать: дробь нехорошая, периодическая… Не годится этот вариант совсем. )
А если сторона плитки 16 см?
Опять подставляем вместо буквы «а» число 16 и повторяем расчёт:
Уже получше. Понадобится 156 полных плиток и ещё четвертинка! Итого 157 плиток. А одну — распиливать на 4 части и брать один кусочек.
Улавливаете идею? Конечно же, самый лучший вариант — когда всё выражение делится нацело! В нашем случае это будет 100 плиток со стороной 20 см.
Видите, какая интересная математическая дуэль у нас с вами разразилась!
Вообще-то, то чем мы с вами только что занимались, называется составлением математической модели задачи. Или математическим моделированием. А алгебра и её методы — верный и надёжный спутник и помощник для математического моделирования и решения такого рода задачек! Намёк понятен? 🙂 Но задачи и их математические модели — это большая тема отдельного урока… А здесь — лишь ознакомительная демоверсия.)
Вообще говоря, если более глубоко подумать, то задачка эта не такая уж и простая, как может показаться. Во-первых, кто сказал, что ванная комната обязательно должна быть именно прямоугольной формы? Это раз. Во-вторых, даже если пол и прямоугольный, то кто сказал, что его размеры обязательно делятся нацело на длину стороны плитки? Это два. Так что вопрос, придётся или не придётся какие-то плитки распиливать (и сколько конкретно плиток распиливать) зависит не только от соотношения площадей, да… Но и от формы пола и его размеров.) Но для прикидочной оценки (сколько вообще плиток заказывать) даже такого грубого подсчёта вполне достаточно.
Что, сложная задачка? Ладно, ремонт в ванной не каждый день делаем, зато за продуктами ходим регулярно. Вот вам задачка попроще. Для отдыха.) Даже не задачка, считать ничего не будем, а лишь так, поразмышляем.
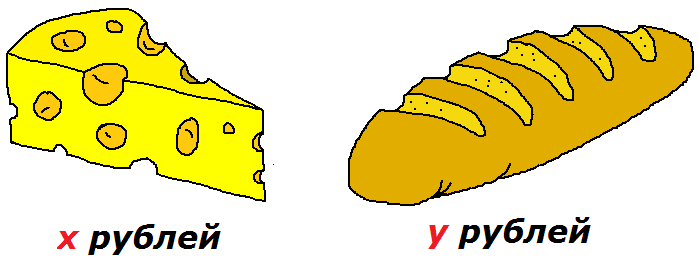
Сыр стоит х рублей, а батон хлеба — у рублей. Каков смысл выражений:
Вот и поразмыслим… Как вы думаете, если вы захотите купить один кусок сыра и один батон хлеба, что вы будете делать, дабы узнать стоимость всей покупки? Конечно! Вы просто сложите цену сыра (х) и цену хлеба (у)! Получится х+у. А уж сколько там сыр с хлебом конкретно стоят в рублях — от конкретного магазина или продавца зависит… А перед алгеброй все магазины и все цены равны: икс плюс игрек — и всё тут.) Вот вам и весь смысл первого выражения.
Уверен теперь, что следующее выражение 2х+3у вас уже не поставит в тупик. За продуктами все ходим.) Догадались? Да! Это будет общая стоимость двух кусков сыра (2х) и трёх батонов хлеба (3у). Улавливаете?)
А х-у? Не всех осеняет сразу… Это выражение ответит нам на вопрос: «На сколько рублей кусок сыра дороже батона хлеба?»
И, наконец, последнее выражение х:у. А за ним какой вопрос скрывается? Правильно! Во сколько раз кусок сыра дороже батона хлеба? Или: «Во сколько раз батон хлеба дешевле куска сыра?» Что одно и то же, да.)
Видите? Каков вопрос задачи, такое и алгебраическое выражение составить надо. Для конкретного вопроса — своё выражение. Но — в общем виде, через буквы. Придём в магазин, посмотрим на ценники, подставим конкретные числа и подсчитаем значение нужного нам выражения. Вот и вся суть.)
А сейчас порешаем простенькие задания самостоятельно. Для привыкания.
3. Время движения лодки по течению реки задаётся формулой t = S:(х+y), где S — расстояние в километрах, х — собственная скорость лодки в км/ч и у — скорость течения реки в км/ч. Пользуясь этой формулой, ответьте на вопросы:
а) Сколько минут плыла лодка 11 км по реке с течением 0,5 км/ч и собственной скоростью 21,5 км/ч?
б) Сколько часов она будет плыть 55 км?
в) Какое расстояние в километрах она проплывёт за пять часов?
Всё получилось? Естественно, уж проще некуда! Что-то не сошлось? Бывает… Внимательнее читаем задание! Где-то время требуется в часах, а где-то часы в минуты надо перевести, да…)
Итак, мы выяснили, что, в отличие от арифметики, в алгебре к числам примешиваются ещё и буквы. Под которыми тоже подразумеваются какие-то числа. Или даже другие выражения. А из этих чиселок и буковок уже можно конструировать самые разнообразные более сложные выражения! Алгебраические выражения.) Простейшие алгебраические выражения и базовые понятия всей алгебры — это одночлен и многочлен. Разберёмся?) В следующем уроке.