Для чего нужна двоичная система
Двоичная система
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:
В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).
Содержание
Таблица умножения двоичных чисел
Использование двоичной системы при измерении дюймами
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7 15 / 16″, 3 11 / 32″ и т. д.
Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1 называется двоичной точкой.
Преобразование двоичных чисел в десятичные
Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | ||||
| 32 | +16 | +2 | +1 |
Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Либо 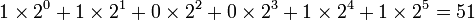
Преобразование методом Горнера
Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.
Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа
Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.
Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.
Другие системы счисления
В статье «Системы счисления (продолжение)» [1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.
См. также
Ссылки
Полезное
Смотреть что такое «Двоичная система» в других словарях:
ДВОИЧНАЯ СИСТЕМА — ДВОИЧНАЯ СИСТЕМА, в математике система счисления, имеющая ОСНОВАНИЕ 2 (десятичная система имеет основание 10). Она наиболее пригодна для работы с компьютерами, поскольку отличается простотой и соответствует двум положениям (открытое 0 и закрытое… … Научно-технический энциклопедический словарь
двоичная система — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN binary system … Справочник технического переводчика
двоичная система — dvejetainė sistema statusas T sritis automatika atitikmenys: angl. binary system vok. Binärsystem, n rus. двоичная система, f pranc. système binaire, m … Automatikos terminų žodynas
двоичная система — dvejetainė sistema statusas T sritis fizika atitikmenys: angl. binary system; dyadic system vok. Binärsystem, n; Dualsystem, n rus. двоичная система, f pranc. système binaire, m … Fizikos terminų žodynas
Двоичная система — Жарг. студ. Шутл. Сильное опьянение. ПБС, 2002 … Большой словарь русских поговорок
Двоичная система счисления — позиционная система счисления с основанием 2, в которой для записи чисел используются цифры 0 и 1. См. также: Позиционные системы счисления Финансовый словарь Финам … Финансовый словарь
ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ — ДВОИЧНАЯ система СЧИСЛЕНИЯ, способ записи чисел, при котором используются две цифры 0 и 1. Две единицы 1 го разряда (т.е. места, занимаемого в числе) образуют единицу 2 го разряда, две единицы 2 го разряда образуют единицу 3 го разряда и т.д.… … Современная энциклопедия
Двоичная система счисления — ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ, способ записи чисел, при котором используются две цифры 0 и 1. Две единицы 1 го разряда (т.е. места, занимаемого в числе) образуют единицу 2 го разряда, две единицы 2 го разряда образуют единицу 3 го разряда и т.д.… … Иллюстрированный энциклопедический словарь
Двоичная система исчисления — система, использующая для представления буквенно цифровых и иных символов наборы комбинаций цифр 1 и 0, основа используемых в цифровых ЭВМ кодов … Издательский словарь-справочник
ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ — позиционная система счисления с основанием 2, в которой имеются две цифры 0 и 1, и их последовательностями записываются все натуральные числа. Напр. цифра 2 записывается как 10, цифра 4 = 22 как 100, число 900 как 11 значное число: 11 110 101 000 … Большая политехническая энциклопедия
Двоичная система счисления
Двоичная система — это один из видов позиционных систем счисления. Основание данной системы равно двум, то есть используется только два символа для записи чисел.
Немного истории
Впервые о данной системе чисел заговорил основоположник математического анализа Г.В. Лейбниц еще в XVII веке. Он доказал, что для данного множества действуют все арифметические операции: сложение, вычитание, умножение и даже деление. Однако вплоть до 30-х годов XX века данную систему не рассматривали всерьез. Но с развитием электронных устройств и ЭВМ, ученые вновь принялись к изучению данной темы, так как двоичная система отлично подходила для программирования и организации хранения данных в памяти компьютеров.
Таблица и алфавит
Кроме того, двоичная система является самой удобной для быстрого перевода в другие системы счисления.
1001102 = 1 ∙ 2 5 + 0 ∙ 2 4 + 0 ∙ 2 3 + 1 ∙ 2 2 + 1 ∙ 2 2 + 0 ∙ 2 0 = 32 + 0 + 0 + 4 + 2 + 0 = 3810
Чтобы наоборот перевести число в двоичную из десятичной, необходимо выполнить его деление на 2 с остатком, а затем записать все остатки в обратном порядке, начиная с частного:
| Делимое | 38 | 19 | 9 | 4 | 2 |
|---|---|---|---|---|---|
| Делитель | 2 | 2 | 2 | 2 | 2 |
| Частное | 19 | 9 | 4 | 2 | 1 |
| Остаток | 0 | 1 | 1 | 0 | 0 |
Для перевода в другие системы необходимо:
Однако можно воспользоваться и более быстрым и удобным способом: разделить знаки двоичного числа на условные группы слева на право (для восьмеричной — по 3 знака; для шестнадцатеричной — по 4 знака), а затем воспользоваться таблицей перевода:
| Двоичная | Восьмеричная | Шестнадцатеричная |
|---|---|---|
| 0 | 0 | 0 |
| 001 | 1 | 1 |
| 010 | 2 | 2 |
| 011 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | |
| 1001 | 9 | |
| 1010 | A | |
| 1011 | B | |
| 1100 | C | |
| 1101 | D | |
| 1110 | E | |
| 1111 | F |
110010012 = 11 001 001 = 011 001 001 = 3118
110010012 = 1100 1001 = С916
Представление двоичных чисел
В двоичной системе также существует понятие «отрицательных» чисел. И для того, чтобы провести какую-либо операцию с ними в двоичном коде, необходимо представить его в виде дополнительного кода. Запись положительного числа при этом не меняется ни для одного из кодов.
Чтобы найти дополнительный код отрицательного числа, необходимо воспользоваться его прямым и дополнительным кодами.
Прямой код предполагает приписывание единицы в начале без изменений записи:
| A > 0 | Aпр = 0A | 1010112; Aпр = 01010112 |
| A ≤ 0 | Aпр = 1|A| | -1010112; Aпр = 11010112 |
Для записи обратного кода цифры заменяют на противоположное значение, первую единицу от прямого кода оставляют без изменений:
| A > 0 | Aобр = 0A | 1010112; Aобр = 01010112 |
| A ≤ 0 | Aобр = 1 A | -1010112; Aобр = 10101002 |
Дополнительный код предполагает использование обратного кода, с той лишь разницей, что к отрицательному числу прибавляют единицу:
| A > 0 | Aдоп = 0A | 1010112; Aдоп = 01010112 |
| A ≤ 0 | Aдоп = 1 A + 1 | -1010112; Aдоп = 10101012 |
Применение двоичной системы в информатике
Двоичная система получила особое распространение в программировании цифровых устройств, так как она соответствует требованиям многих технических устройств, поддерживающих два состояния (есть ток, нет тока). Кроме того, является более простой и надежной для кодирования информации. Именно поэтому программный код большей части ЭВМ основан именно на двоичной системе счисления.
Почему в ЭВМ используется двоичная система счисления
В отличие от человека – ЭВМ не умеют мыслить. Они не способны подрожать человеческому воображению. Однако компьютеры могут очень быстро выполнять сложные математические расчеты и решать за секунды задачи, на которые у нас могли уходить целые недели. Все данные, которые есть в ПК, записаны в цифровом коде, алфавит которого состоит из двух символов – нуля и единицы. В этой статье вы узнаете ответ на вопрос — почему в ЭВМ используется двоичная система счисления.
Ликвидация безграмотности
Введение для чайников
Итак, для того чтобы понять почему двоичный код используется в ЭВМ нужно иметь о нем базовое представление. Все Вы знакомы с десятичным представлением чисел – в нем используются знаки (цифры) от нуля до девяти. После того, как вы использовали цифры от 0 до 9, разряд единиц обнуляется и идет переход к следующему порядку — получается число 10. Использовав все комбинации из двух цифр (отсчитав до 99), вы переходите к разряду сотен.
Отсюда можно сделать вывод, что в десятичной форме записи – цифра следующего разряда всегда в десять раз больше, чем предыдущая (1,10,100,1000 и т.д.). Аналогичное правило применимо и к двоичному коду, состоящему из последовательности нулей и единиц – каждый следующий разряд в два раза больше предыдущего. Чтобы вам было понятнее, покажем это наглядно.
Цифровая арифметика в информатике
В двоичном счислении, исходя из предыдущего раздела, 1 будет представлена, как 1, 2-10,4-100,8-1000. Именно в таком двоичном представлении компьютер работает с вашими данными и неважно, какую форму они имеют – графическую, музыкальную или текстовую. Абсолютно вся информация в корпусе вашего ПК зашита в виде комбинации из нулей и единиц.
Один нолик или однёрка называется единицей информации, или как его еще принято называть – «бит». Наверное, каждый, кто работал с ЭВМ или увлекался информатикой, слышал про магическое число 256. Почему оно так называется? Это количество знаков, которое может распознать компьютер по их коду. Сюда входят кириллический алфавит, латинские буквы цифры и другие символы вроде знаков препинания. Для того чтобы кодировать один символ в ЭВМ нужно 8 бит памяти. Почему?
А 8 бит, принято в информатике называть, как один байт – количество памяти необходимое для хранения одного символа. Зная всё это можно перейти к главному вопросу:
Почему в ЭВМ используется двоичная система счисления
Почему использовалась в начале эры ЭВМ?
Ответ прост — на это повлияли законы физики и особенности развития аппаратного обеспечения. Вспомните, как выглядели первые ЭВМ – большие установки, которые занимали по площади размер, сопоставимый с теннисным кортом.
Для отображения битов и проведения операций с ними использовались обычные лампочки «Ильича» (лампы накаливания). Если на лампу подавался ток, то она обозначала единицу, если ток не подавался, и лампа не горела – 0. Всё это управлялось с помощью электронного реле. Почему разработчики приняли решение реализовать все именно так? Здесь можно выделить несколько главных причин:
Второй и третий плюс вытекают из первого. Да и в то время технологии были не настолько развиты, чтобы можно было предложить более практичное решение. Революция произошла в конце пятидесятых, начале шестидесятых годов, когда были выпущены первые кремниевые транзисторы.
Почему мы пользуемся ей сейчас?
Сейчас будет сложно, так что приготовьтесь. Процессоры всех современных компьютеров и других цифровых устройств работают на основе схемотехнических элементов, которые называются транзисторы.
Итак, что это такое? Если говорить просто, то это элемент, который позволяет управлять электрическим током. Рассмотрим принцип его действия.
Элемент состоит из трех частей:
Здесь вам нужно знать несколько моментов. В N области содержатся частицы с отрицательным зарядом (электроны). В P области содержатся носители положительного заряда, так называемые «дырки». Между ними располагается так называемый обедненный слой. В нем содержится некоторое количество электронов.
Если подать одноименное напряжение на источник и минусовое на управляющую ногу, то потечет ток в сторону выхода – это будет 1, а если наоборот, то ток идти не будет – что будет равно 0. Менять свое состояние устройство может ОЧЕНЬ быстро. Если вы не поняли, как это работает — не страшно. Главное поймите, что элемент делает.
Однако грош цена была бы этому изобретению – если с помощью транзистора можно было выводить только нуль и единицу. Почему? Какой смысл от букв и цифр, если мы не можем с ними выполнять различные операции.
Однако подключив два транзистора определенным образом, мы сможем выполнять логические действия, такие как «или» (сложение) и «и» (умножение). Также можно менять значения на выходе, меняя напряжения на входе. Таким образом, получаются различные комбинации нулей и единиц.
Вывод
А теперь подумайте, какую еще систему можно использовать в компьютере и почему? Например, возьмем следующее по счету — троичное счисление. Система должна находиться в одном из трех состояний. Какой физический процесс подойдет для отображения данных?
Если же брать три уровня тока, то какое устройство сможет быстро производить с ними операции? Правильно, такого не существует. На данный момент, как и раньше, нет более удобного и простого аналога представления информации – это и будет являться ответом на вопрос: почему в ЭВМ используется двоичная система счисления.
Как объяснять двоичную систему счисления
Кто-то только входит в IT-мир, кто-то объясняет информатику своему чаду.
Довольно быстро вы обнаружите, что не так-то просто объяснить, как работает двоичный счёт.
Это вам очевидно, что после 11 идёт 100, а новичку это ещё долго может быть непонятно.
Так вот, чтобы увеличить скорость понимания, мы решили сделать дидактический материал.
Проблема
Важно отметить, что даже распиаренный курс Гарвардского университета по компьютерным наукам «CS50» не помогает.
Парень из американского университета просто заявляет, что «нуль — это нуль», «один — это один», а потом идёт 10, а потом 11. Понятно? Думаю, нет. Вот спросите кого-то, кто не программист, а каким будет следующее число — высока вероятность, что он не сможет ответить. Слишком быстро проскочили идею о переносе разряда.
То же самое касается школьных методов перевода: во-первых, методы эти академически сухи, во-вторых, не интуитивны — например, не очевидно, почему после каскадного деления на 2 нужно ставить биты задом наперёд.
А если непонятно, то и не интересно. А если нет интереса, то и запоминается с трудом.
Мы это всё учли, и решили сделать интересное и постепенное объяснение.
Что мы предлагаем
Сначала нужно объяснить, как вообще работает обычная десятичная система счисления — и про конечный «алфавит» цифр, и про идею переноса разряда. Так развивается понимание принципа «системы счисления».
Только потом можно переходить к идее двоичной системы — и вот обучаемый уже медленно, но довольно уверенно говорит «1, 10, 11, 100».
Далее, мы решили попробовать совсем не школьный метод — объяснение двоичного счёта на пальцах: это когда загнутый палец это 0, а разогнутый это 1.
Я проверял это на подростках: показываешь им: «это 1, это 2, это 3 — теперь покажите мне 4». И весь класс сосредоточенно, медленно показывает средние пальцы. Отличницы в эсхатологическом восторге, задние парты тыкают друг другу в лицо и кричат «на тебе четвёрку!».
Провокативно? Да. Запоминается? 100%.
Теперь, когда тема стала «своей», можно переходить к теме перевода чисел из одной системы счисления в другую — начать лучше с классического школьного сухого перевода (если честно, то больше чтобы постращать).
А уже потом с помощью анимации объяснить идею перевода прямо на пальцах, и потом опять же на пальцах пересчитать число 132 в средние пальцы уже на обеих руках.
На десерт показываем, где двоичная и 16-ричная системы применяется в реальной жизни.
Двоичная система — это например QR-коды вокруг нас.
А 16-ричная система это в основном коды цветов в CSS и хеши разных стилей, от MD5 до UUID.
Итак, вот весь пакет видео-уроков (они бесплатные, в Ютубе):
Учебник | Двоичная система счисления
Человек научился считать с помощью пальцев. Десять пальцев были первым инструментом счета, в котором каждому загнутому пальцу соответствовал один предмет. Счет десятками (его со временем стали называть десятичной системой счисления, или десятеричной) оказался настолько удобным, что живет до сих пор.
Затем та же десятичная система перекочевала и в электромеханические счетные машины. В них был применен шаговый искатель с десятью позициями.
Почему же не использовать тогда двоичную систему счисления? Ведь в ней только две цифры: 0 и 1. А это удобно для работы на электронной машине. И новые машины стали считать с помощью 0 и 1.
Потом о двоичной системе забыли. В течение почти 200 лет на эту тему не было издано ни одного труда. Вернулись к ней только в 1931 году, когда были продемонстрированы некоторые возможности практического применения двоичного счисления.
Как записывают числа в двоичной системе
Чем меньше знаков-цифр в одном разряде для записи в двоичной системе, тем больше надо разрядов, чтобы представить данное число. Возьмем, например число 8. В двоичной системе для его представления понадобятся четыре разряда: 1000.
Попробуем записать какое-нибудь число, допустим 1017, в двоичной системе. Для этого, как и в десятичной системе, раскладываем его на разряды, но разряды здесь выглядят по-иному. Начнем с низшего, с 7. Поскольку в двоичной системе каждый разряд в два раза больше последующего, число 7 запишется суммой трех двоичных разрядов: 7=4+2+ 1 (1 в 2 раза меньше 2; 2 в 2 раза меньше 4). В числе 7 одна четверка, одна двойка, одна единица: 7=4+2+ 1. Эту запись можно сделать по другому: 1*2 2 + 1*2 1 + 1. Следовательно, в каждом из этих разрядов ставим по 1-111.
Основы двоичной системы, столь непривычной из-за традиции оперировать всегда и везде системой десятичной, мы знаем. Двоичной системой пользуются только вычислительные машины. Машина пересчитывает нули и единицы с очень большой скоростью.






