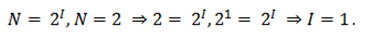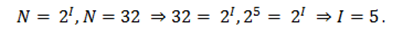Для чего нужна формула хартли

Формула Хартли

Из Википедии — свободной энциклопедии

Формула Хартли или хартлиевское количество информации или мера Хартли — логарифмическая мера информации, которая определяет количество информации, содержащееся в сообщении.

Где N — количество символов в используемом алфавите (мощность алфавита), K — длина сообщения (количество символов в сообщении), I — количество информации в сообщении в битах.

Формула была предложена Ральфом Хартли в 1928 году как один из научных подходов к оценке сообщений.

Для случая определения количества информации i в одном символе алфавита мощности N, формула Хартли принимает вид:

Соответственно, мощность алфавита равна:

Из формулы Хартли следует, что алфавит, содержащий только 1 символ не может быть использован для передачи информации:

Пусть, имеется алфавит А, из N букв которого составляется сообщение:

Количество возможных вариантов разных сообщений:

где M — возможное количество различных сообщений, N — количество букв в алфавите, K — количество букв в сообщении.

Рассмотрим следующий пример. Цепь ДНК состоит из 4 видов азотистых оснований: Аденин (A), Гуанин (G), Тимин (T), Цитозин (C). Следовательно, мощность «алфавита» ДНК N равна 4. Значит, каждое азотистое основание несет i = log 2 ⁡ 4 = 2 <\displaystyle i=\log _<2>4=2> бита информации.

Пример: Пусть алфавит состоит из 16 символов «1», «2», «3», «4», «5», «6», «7», «8», «9», «0», «+», «-», «*», «/», «^», «#», а длина сообщения составляет 10 символов (например, команда «*123*1*3^#») — таким образом, мощность алфавита N = 16, а длина сообщения K = 10. При выбранных нами алфавите и длине сообщения можно составить M = N K = 16 10 = 1099511627776 <\displaystyle M=N^=16^<10>=1099511627776> сообщений. По формуле Хартли можно определить, что количество информации в каждом символе одного из этих сообщений равно i = log 2 ⁡ N = log 2 ⁡ 16 = 4 <\displaystyle i=\log _<2>N=\log _<2>16=4> бита, а количество информации во всем сообщении, соответственно, равно I = K log 2 ⁡ N = 10 log 2 ⁡ 16 = 10 ⋅ 4 = 40 <\displaystyle I=K\log _<2>N=10\log _<2>16=10\cdot 4=40> бит.

Источник

Для чего нужна формула хартли

1.2. Формула Хартли измерения количества информации. Закон аддитивности информации

Как уже упоминалось выше, в качестве основной единицы измерения информации мы будем использовать бит. Соответственно, с точки зрения алфавитного подхода мы будем кодировать информацию при помощи нулей и единиц (двоичных знаков).

Для того чтобы измерить количество информации в сообщении, надо закодировать сообщение в виде последовательности нулей и единиц наиболее рациональным способом, позволяющим получить самую короткую последовательность. Длина полученной последовательности нулей и единиц и является мерой количества информации в битах.

Поставим себе одну из наиболее часто встречающихся задач в теории информации. Пусть у нас есть `N` возможных равновероятных вариантов исходов некоторого события. Какое количество информации нам нужно получить, чтобы оставить только один вариант?

Например, пусть мы знаем, что некоторая интересная для нас книга находится на одной из полок нашего книжного шкафа, в котором `8` полок. Какое количество информации нам нужно получить, чтобы однозначно узнать полку, на которой находится книга?

Решим эту задачу с точки зрения содержательного и алфавитного подходов. Поскольку изначально в шкафу было `8` полок, а в итоге мы выберем одну, следовательно, неопределённость знания о местоположении книги уменьшится в `8` раз. Мы говорили, что один бит – это количество информации, уменьшающее неопределённость знания в `2` раза. Следовательно, мы должны получить `3` бита информации.

Теперь попробуем использовать алфавитный подход. Закодируем номера всех полок при помощи `0` и `1`. Получим следующие номера: `000, 001, 010, 011, 100, 101, 110, 111`. Для того чтобы узнать, на какой полке находится книга, мы должны узнать номер этой полки. Каждый номер состоит из `3` двоичных знаков. А по определению, `1` бит (в алфавитном подходе) – это количество информации в сообщении, состоящем из `1` двоичного знака. То есть мы тоже получим `3` бита информации.

Прежде чем продолжить рассмотрение поставленной общей задачи введём важное математическое определение.

Назовём логарифмом числа `N` по основанию `a` такое число `X`, что Обозначение:

На параметры логарифма налагаются некоторые ограничения. Число `N` обязательно должно быть строго больше `0`. Число `a` (основание логарифма) должно быть также строго больше нуля и при этом не равняться единице (ибо при возведении единицы в любую степень получается единица).

Теперь вернёмся к нашей задаче. Итак, какое же количество информации нам нужно получить, чтобы выбрать один исход из `N` равновероятных? Ответ на этот вопрос даёт формула Хартли: `H=log_aN`, где `N` – это количество исходов, а `H` – количество информации, которое нужно получить для однозначного выбора `1` исхода. Основание логарифма обозначает единицу измерения количества информации. То есть если мы будем измерять количество информации в битах, то логарифм нужно брать по основанию `2`, а если основной единицей измерения станет трит, то, соответственно, логарифм берётся по основанию `3`.

Рассмотрим несколько примеров применения формулы Хартли.

В библиотеке `16` стеллажей, в каждом стеллаже `8` полок. Какое количество информации несёт сообщение о том, что нужная книга находится на четвёртой полке?

Решим эту задачу с точки зрения содержательного подхода. В переданном нам сообщении указан только номер полки, но не указан номер стеллажа. Таким образом, устранилась неопределённость, связанная с полкой, а стеллаж, на котором находится книга, мы всё ещё не знаем. Так как известно, что в каждом стеллаже по `8` полок, следовательно, неопределённость уменьшилась в `8` раз. Следовательно, количество информации можно вычислить по формуле Хартли `H=log_2 8=3` бита информации.

Имеется `27` монет, одна из которых фальшивая и легче всех остальных. Сколько потребуется взвешиваний на двухчашечных весах, чтобы однозначно найти фальшивую монету?

В этой задаче неудобно использовать бит в качестве основной единицы измерения информации. Двухчашечные весы могут принимать три положения: левая чаша перевесила, значит, фальшивая монета находится в правой; правая чаша перевесила, значит, монета находится в левой; или же весы оказались в равновесии, что означает отсутствие фальшивой монеты на весах. Таким образом, одно взвешивание может уменьшить неопределённость в три раза, следовательно, будем использовать в качестве основной единицы измерения количес-тва информации трит.

По формуле Хартли `H = log _3 27 = 3` трита. Таким образом, мы видим, что для того чтобы найти фальшивую монету среди остальных, нам потребуется три взвешивания.

Логарифмы обладают очень важным свойством: `log_a(X*Y)=log_aX+log_aY`.

Если переформулировать это свойство в терминах количества информации, то мы получим закон аддитивности информации: Коли-чество информации`H(x_1, x_2)`, необходимое для установления пары `(x_1, x_2)`, равно сумме количеств информации `H(x_1)` и `H(x_2)`, необходимых для независимого установления элементов `x_1` и `x_2`:

Проиллюстрируем этот закон на примере. Пусть у нас есть игральная кость в форме октаэдра (с `8` гранями) и монета. И мы одновременно подбрасываем их вверх. Нужно узнать, какое количество информации несёт сообщение о верхней стороне монеты после падения (орёл или решка) и числе, выпавшему на игральной кости.

Игральная кость может упасть `8` различными способами, следовательно, по формуле Хартли можно вычислить, что, определив число, выпавшее на игральной кости, мы получаем `3` бита информации. Соответственно, монета может упасть только `2` способами и несёт в себе `1` бит информации. По закону аддитивности информации мы можем сложить полученные результаты и узнать, что интересующее нас сообщение несёт `4` бита информации.

Если в результате вычислений по формуле Хартли получилось нецелое число, а в задаче требуется указать целое число бит, то результат следует округлить в большую сторону.

Источник

Содержательный подход. Формулы Хартли и Шеннона.

Американский инженер Р. Хартли в 1928 г. процесс получения информации рассматривал как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определял как двоичный логарифм N.

Формула Хартли: I = log₂N или N = 2 i

Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log₂100 > 6,644. Таким образом, сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицы информации.

Приведем другие примеры равновероятных сообщений:

1. при бросании монеты: «выпала решка», «выпал орел»;

2. на странице книги: «количество букв чётное», «количество букв нечётное».

Определим теперь, являются ли равновероятными сообщения«первой выйдет из дверей здания женщина»и«первым выйдет из дверей здания мужчина». Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины.

Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.

где p_i — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.

Помимо двух рассмотренных подходов к определению количества информации, существуют и другие. Важно помнить, что любые теоретические результаты применимы лишь к определённому кругу случаев, очерченному первоначальными допущениями.

В качестве единицы информации Клод Шеннон предложил принять один бит (англ. bit — binary digit — двоичная цифра).

Бит в теории информации — количество информации, необходимое для различения двух равновероятных сообщений (типа «орел»—«решка», «чет»—«нечет» и т.п.).

В вычислительной технике битом называют наименьшую «порцию» памяти компьютера, необходимую для хранения одного из двух знаков «0» и «1», используемых для внутримашинного представления данных и команд.

Бит — слишком мелкая единица измерения. На практике чаще применяется более крупная единица — байт, равная восьми битам. Именно восемь битов требуется для того, чтобы закодировать любой из 256 символов алфавита клавиатуры компьютера (256=2 8 ).

Широко используются также ещё более крупные производные единицы информации:

1 Килобайт (Кбайт) = 1024 байт = 210 байт,

1 Мегабайт (Мбайт) = 1024 Кбайт = 220 байт,

1 Гигабайт (Гбайт) = 1024 Мбайт = 230 байт.

В последнее время в связи с увеличением объёмов обрабатываемой информации входят в употребление такие производные единицы, как:

1 Терабайт (Тбайт) = 1024 Гбайт = 240 байт,

1 Петабайт (Пбайт) = 1024 Тбайт = 250 байт.

За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных сообщений. Это будет не двоичная (бит), а десятичная (дит) единица информации.

Количество информации, заключенное в сообщении, определяется объемом знаний, который несет это сообщение получающему его человеку. Сообщение содержит информацию для человека, если заключенные в нем сведения являются для этого человека новыми и понятными, и, следовательно, пополняют его знания.

При содержательном подходе возможна качественная оценка информации: полезная, безразличная, важная, вредная, … Одну и туже информацию разные люди могут оценить по-разному.

Информацию, которую получает человек, можно считать мерой уменьшения неопределенности знаний. Если некоторое сообщение приводит к уменьшению неопределенности наших знаний, то можно говорить, что такое сообщение содержит информацию.

За единицу количества информации принято такое количество информации, которое мы получаем при уменьшении неопределенности в 2 раза. Такая единица названа бит.

В компьютере информация представлена в двоичном коде или на машинном языке, алфавит которого состоит из двух цифр (0 и 1). Эти цифры можно рассматривать как два равновероятных состояния. При записи одного двоичного разряда реализуется выбор одного из двух возможных состояний (одной из двух цифр) и, следовательно, один двоичный разряд несет количество информации в 1 бит. Два двоичных разряда несут информацию 2 бита, три разряда – 3 бита и т.д.

Поставим теперь обратную задачу и определим: «Какое количество различных двоичных чисел N можно записать с помощью I двоичных разрядов?» С помощью одного двоичного разряда можно записать 2 различных числа (N=2=2 1 ), с помощью двух двоичных разрядов можно записать четыре двоичных числа (N=4=2 2 ), с помощью трех двоичных разрядов можно записать восемь двоичных чисел (N=8=2 3 ) и т.д.

В общем случае количество различных двоичных чисел можно определить по формуле

где I – количество информации;

N – количество возможных событий (равновероятных). ;

В математике существует функция, с помощью которой решается показательное уравнение, эта функция называется логарифмом. Решение такого уравнения имеет вид:

.

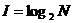
Если события равновероятны, то количество информации определяется по данной формуле.

Количество информации для событий с различными вероятностями определяется по формуле Шеннона:

,

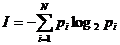
где I – количество информации;

N – количество возможных событий;

P_i – вероятность отдельных событий.

Пример 3.4

В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере (например, выпал номер 15)?

Поскольку вытаскивание любого из 32 шаров равновероятно, то количество информации об одном выпавшем номере находится из уравнения: 2 I =32.

Пример 3.5

Какое количество вопросов достаточно задать вашему собеседнику, чтобы наверняка определить месяц, в котором он родился?

Будем рассматривать 12 месяцев как 12 возможных событий. Если спрашивать о конкретном месяце рождения, то, возможно, придется задать 11 вопросов (если на 11 первых вопросов был получен отрицательный ответ, то 12-й задавать не обязательно, так как он и будет правильным).

Правильнее задавать «двоичные» вопросы, то есть вопросы, на которые можно ответить только «да» или «нет». Например, «Вы родились во второй половине года?». Каждый такой вопрос разбивает множество вариантов на два подмножества: одно соответствует ответу «да», а другое – ответу «нет».

Правильная стратегия состоит в том, что вопросы нужно задавать так, чтобы количество возможных вариантов каждый раз уменьшалось вдвое. Тогда количество возможных событий в каждом из полученных подмножеств будет одинаково и их отгадывание равновероятно. В этом случае на каждом шаге ответ («да» или «нет») будет нести максимальное количество информации (1 бит).

По формуле 2 и с помощью калькулятора получаем:

бита.

Количество полученных бит информации соответствует количеству заданных вопросов, однако количество вопросов не может быть нецелым числом. Округляем до большего целого числа и получаем ответ: при правильной стратегии необходимо задать не более 4 вопросов.

Пример 3.6

После экзамена по информатике, который сдавали ваши друзья, объявляются оценки («2», «3», «4» или «5»). Какое количество информации будет нести сообщение об оценке учащегося А, который выучил лишь половину билетов, и сообщение об оценке учащегося В, который выучил все билеты.

Опыт показывает, что для учащегося А все четыре оценки (события) равновероятны и тогда количество информации, которое несет сообщение об оценке, можно вычислить по формуле (1):

бита.

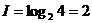
На основании опыта можно также предположить, что для учащегося В наиболее вероятной оценкой является «5» (p₁=1/2), вероятность оценки «4» в два раза меньше (p₂=1/4), а вероятности оценок «2» и «3» еще в два раза меньше (p₃ =p₄=1/8). Так как события неравновероятны, воспользуемся для подсчета количества информации в сообщении формулой 2:

бита

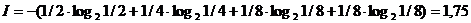
Вычисления показали, что при равновероятных событиях мы получаем большее количество информации, чем при неравновероятных событиях.

Пример 3.7

В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика.

Так как количество шариков разного цвета неодинаково, то вероятности зрительных сообщений о цвете вынутого из мешочка шарика также различаются и равны количеству шариков данного цвета деленному на общее количество шариков:

События неравновероятны, поэтому для определения количества информации, содержащегося в сообщении о цвете шарика, воспользуемся формулой 2:

бит

Для вычисления этого выражения, содержащего логарифмы можно воспользоваться калькулятором. I»1,85 бита.

Пример 3.8

Используя формулу Шеннона, достаточно просто определить, какое количество бит информации или двоичных разрядов необходимо, чтобы закодировать 256 различных символов. 256 различных символов можно рассматривать как 256 различных равновероятных состояний (событий). В соответствии с вероятностным подходом к измерению количества информации необходимое количество информации для двоичного кодирования 256 символов равно:

I=log₂256=8 бит=1 байт

Следовательно, для двоичного кодирования 1 символа необходим 1 байт информации или 8 двоичных разрядов.

Какое количество информации содержится, к примеру, в тексте романа «Война и мир», во фресках Рафаэля или в генетическом коде человека? Ответа на эти вопросы наука не даёт и, по всей вероятности, даст не скоро. А возможно ли объективно измерить количество информации? Важнейшим результатом теории информации является следующий вывод:«В определенных, весьма широких условиях можно пренебречь качественными особенностями информации, выразить её количество числом, а также сравнить количество информации, содержащейся в различных группах данных».

В настоящее время получили распространение подходы к определению понятия «количество информации», основанные на том, что информацию, содержащуюся в сообщении, можно нестрого трактовать в смысле её новизны или, иначе, уменьшения неопределённости наших знаний об объекте. Эти подходы используют математические понятия вероятности и логарифма.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник

Алфавитный подход к оценке количества информации. Формула Хартли

Вы будете перенаправлены на Автор24

Содержательный подход к оценке количества информации, который мы рассматривали ранее, измеряет ее количество, как уменьшение неопределенности наших знаний.

Однако любое техническое устройство не способно воспринимать непосредственно содержание информации, оно лишь понимает наличие или отсутствие электрических сигналов. Вследствие чего в вычислительной технике вынуждены использовать другой подход к оценке количества информации, который называется алфавитным.

Принцип алфавитного подхода к оценке количества информации

Алфавитный подход строится на принципе, утверждающем, что любое сообщение можно представить в виде кодов с помощью конечной последовательности символов, содержащейся в любом алфавите. Носители информации содержат любые последовательности символов, которые могут храниться, передаваться и обрабатываться как с помощью человека, так и с помощью технических устройств, в частности компьютера. Этот подход описал А.Н. Колмогоров, согласно которому, информативность, заключающаяся в последовательности символов, не может зависеть от содержания самого сообщения, а может определяться лишь минимальным количеством символов, необходимых для ее кодирования. Подобный подход к оценке количества информации носит объективный характер, так как не зависит от получателя, принимающего сообщения. Смысл же сообщений может учитываться только на этапе выбора алфавита кодирования либо не учитываться совсем.

В основу принципа этого подхода лег подсчет числа символов в сообщении, таким образом, важна только длина сообщения и совсем не учитывается его содержание. Однако на длину сообщения может влиять мощность алфавита используемого языка.

Мощность алфавита и информационная емкость. Формула Хартли

Все множество символов, из которых состоит язык, можно традиционно назвать алфавитом. Как правило, под алфавитом понимаются только буквы, но кроме них при написании текстов используются знаки препинания, цифры, скобки, пробелы, их тоже, в свою очередь, можно включить в алфавит.

Например:

Готовые работы на аналогичную тему

При алфавитном подходе считают, что каждый символ текста несет в себе определенную информационную емкость, которая, в свою очередь, зависит от мощности алфавита.

Хартли утверждал, что на количество информации, содержащейся в сообщении, может влиять фактор неожиданности, который, в свою очередь, зависит от вероятности получения сообщения. Если эта вероятность получения сообщения высокая, а неожиданность при этом низкая, то сообщение будет содержать мало полезной для человека информации.

Однако при создании своей формулы Р.Хартли полностью исключил фактор неожиданности. Формула Хартли работает только в том случае, когда появление символов равновероятно и они статистически независимы.

Например, с помощью приведенной формулы можно определить количество информации, которое несет знак в двоичной системе счисления:

Информационная емкость знака двоичной системы составляет 1 бит.

Необходимо определить информационную емкость буквы русского алфавита (без учета буквы «ё»).

Решение:

Представим себе, что текст к нам поступает последовательно, по одному знаку, словно бумажная лента, выползающая из телеграфного аппарата. Предположим, что каждый символ, который появляется на ленте, с равной вероятностью может быть любым символом алфавита. В действительности это не совсем так, но для упрощения примем такое предположение.

Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.

Количество информации в сообщении можно определить, используя формулу:

Рассмотрим пример решения задачи

Решение. Чтобы решить задачу, для начала определим количество знаков в сообщении и мощность используемого алфавита.

Необходимо определить какое количество информации содержит слово «Привет».

Однако мы не сможем воспользоваться этой формулой, поскольку нам не известно какое количество информации несет один знак ($I$).

Единицы измерения информации

Проведем несложный расчет и получим, что страница содержит:

$50 \cdot 60 = 3000$ байт информации.

Объем же информации, содержащейся в книге:

$3000 \cdot 50 = 150 \ 000$ байт.

Любая система единиц измерения содержит основные единицы и производные от них.

При измерении больших объемов информации на практике широко используются следующие производные от байта единицы, которые приведены в таблице:

Источник