Для чего нужна гравитация api
ru.knowledgr.com
Таким образом, плотность API является внутренней мерой плотности петролейной жидкости по сравнению с плотностью воды (также известной как удельная плотность). Используется для сравнения плотностей петролеума. Например, если одна жидкость петролея меньше дензе, чем другая, она имеет большую плотность API. Хотя гравитация API безразмерной величины (см. формулу ниже), она называется в градусах. Плотность АПИ в градусах на гидрометрическом приборе. Значения плотности API большинства петролеумов находятся в диапазоне от 10 до 70 градусов.
В 1916г. Национальное бюро стандартов США приняло шкалу Зе, которая была разработана во Франции в 1768 г., как стандарт США для измерения удельной плотности менее дензе, чем вода. Расследование, проведенное Национальной академией наук США, выявило серьезные ошибки в контроле солености и температуры, которые вызвали серьезные отклонения в опубликованных значениях. Hydrom в США был активирован и широко распространен с модулем 141,5 вместо модуля шкалы Се 140. Шкала была настолько прочно установлена, что к 1921г. исправленная, реализованная Американским институтом Петролея, должна была создать шкалу гравитации API, признававшую фактически используемую шкалу.
Формулы плотности API
Формула расчета плотности API на основе удельной плотности (Specific Gravity, Specific Gravity):
И наоборот, удельная плотность петролея может быть из их значения плотности API как
Таким образом, тяжелая нефть с удельной плотностью 0 (т.е. с той же плотностью, что и чистая вода при 60 ° F) имеет плотность API:
Использование силы тяжести API для расчета баррелей сырой нефти на метрическую тонну
В нефтяной промышленности количество сырой нефти часто измеряется в метрических тоннах. Можно вычислить приблизительное количество баррелей на метрическую тонну для данной крайдовой нефти, исходя из ее гравитации API:
Например, метрическая тонна интермедиата Западного Техаса (39,6 ° API) имеет объём около 7,6 баррелей.
Измерение плотности API по ее удельной плотности
Для снижения плотности АПИ сначала измеряют удельную плотность (то есть плотность относительно воды) с использованием либо гидрометра, подробно описанного в ASTM D1298, либо метода окаймляющей U-образной трубки, описанного в ASTM D4052.
Регулировки плотности при различных температурах, для расширения и сокращения стекла soda-lim и мениска для непрозрачных масел подробно описаны в таблицах измерений Petroleum, подробности использования указаны в ASTM D1250. Удельная плотность определяется приведенной ниже формулой.
Прямое измерение плотности API (метод Гидрометра)
Классификации или классы
В целом, нефть с интенсивностью АПИ между 40 и 45 ° соответствует самым высоким ценам. Выше 45 ° молекулярные цепи становятся ши и менее способны к нефтеперерабатывающим заводам.
Нефть Crude классифицируется как легкая, средняя или тяжелая в соответствии с измеренной плотностью API.
Однако не все стороны используют одинаковый градинг. Геологическая съемка Соединенных Штатов использует несколько иные диапазоны.
Круидовая нефть с плотностью АПИ менее 10 ° называется сверхтяжелой нефтью или битумом. Битумные, выращенные из нефтеносных песков, отложений в Тта, Канада, имеют плотность API около 8 °. Он может быть разбавлен липогидрокарбонами для получения разбавленного битума, который имеет плотность API менее 22,3 °, или далее «» до плотности API от 31 до 33 ° в качестве синтетического crude.
JavaScript для продвинутых: пишем симулятор гравитации
Космос трудно понять — или люди склонны так думать. Но в этом уроке мы увидим, что законы, управляющие движением звёзд, планет, астероидов и даже целых галактик, невероятно просты. Если бы наша Вселенная была создана разработчиком, он наверняка был бы обеспокоен написанием чистого кода, который легко поддерживать и масштабировать.
Мы собираемся создать симуляцию внутренней области нашей Солнечной системы, используя только старый добрый JavaScript. Это будет гравитационная N-объектная симуляция, где каждый объект испытывает на себе гравитацию всех других объектов симуляции.
Мы также посмотрим, как позволить пользователям добавлять свои собственные планеты при помощи небольшого движения мыши, и вызывать при этом всевозможный космический беспорядок. Ещё мы разберёмся, как создать несколько необычных траекторий движения тел, в дополнение к некоторым другим фишкам, которые сделают симулятор более увлекательным для обычного пользователя.
Примечание Это руководство предполагает, что у вас есть базовые знания JavaScript, а также синтаксиса и нововведений, представленных в ES6.
Написание алгоритма для N-объектной симуляции
Для написания алгоритма мы будем опираться на численное интегрирование. Оно хорошо подходит для решения гравитационных N-объектных задач, в которых оперируют позициями и скоростями всех объектов в данный момент времени T, вычисляют гравитационную силу, с которой они действуют друг на друга, и изменяют их скорости и позиции во времени (T + dt, dt — изменение во времени). Применяя это, мы можем проследить траектории множества тел в пространстве и времени.
Для моделирования будем использовать декартову систему координат. Преимущество использования такой системы координат для моделирования в том, что Canvas API, с помощью которого мы будем визуализировать моделирование, также её использует.
Для написания алгоритма необходимо иметь представление о том, что подразумевается под скоростью и ускорением. Скорость — это изменение положения объекта во времени, а ускорение — изменение скорости объекта во времени. Первый закон Ньютона гласит, что каждый объект будет оставаться в покое или двигаться равномерно и прямолинейно, если на него не будут воздействовать никакие внешние силы. Земля не движется по прямой линии, а вращается вокруг Солнца, поэтому она ускоряется. Это ускорение вызывают гравитационные силы Солнца и других планет и объектов во Вселенной, действующие на Землю.
Преобразуем вышесказанное в код для обновления векторов ускорения всех тел.
В текущих вычислениях не хватает единиц измерения. Логично будет выбрать шкалу, которая подходит для рассматриваемых величин, чтобы избежать неуклюжих длинных чисел. В случае с нашей Солнечной системой учёные склонны использовать астрономические единицы для расстояния, солнечную массу для сравнения с другими телами и года для времени. Принимая этот набор единиц, значение гравитационной постоянной g составляет 39,5. Для определения векторов положения и скорости всех тел обратимся к веб-интерфейсу HORIZONS, созданному NASA JPL, где изменим выходную настройку на векторные таблицы, а единицы — на астрономические единицы и дни. По какой-то причине Horizons не измеряет векторы годами в качестве единицы времени. Поэтому мы должны умножить векторы скорости на 365,25 (количество дней в году), чтобы получить векторы скорости, которые согласуются с нашим выбором единиц измерения времени (годы).
Класс JavaScript кажется отличным способом инкапсуляции методов, которые мы написали выше. Сделаем некоторый рефакторинг:
Для продвижения симуляции на следующий шаг вызываем:
Создание визуального отображения небесных тел
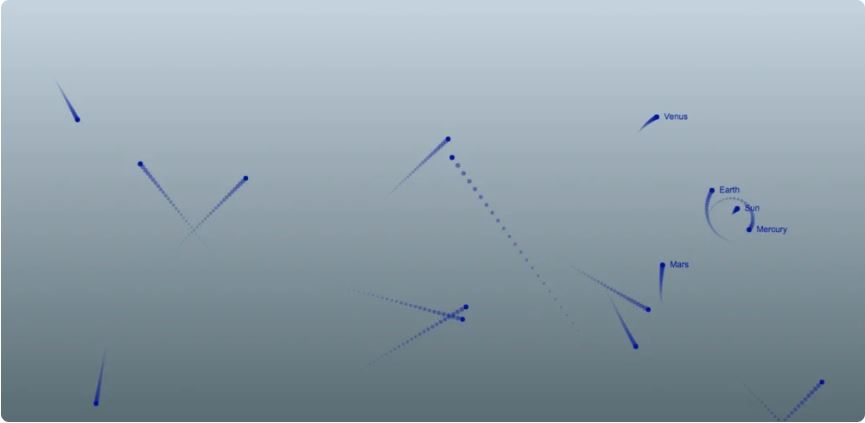
Можно было бы представить тела маленькими кружками, созданными с помощью метода arc() в Canvas API, но визуализация траекторий тел в пространстве и времени была бы сложной. Поэтому напишем класс, который будет шаблоном для визуального отображения тел. Создадим круг, который оставляет за собой заранее определённое количество меньших по размеру и поблёкших кружков и передаёт движение и направление. Чем дальше вы удаляетесь от текущей позиции тела, тем меньшие по размеру и более затухающие будут круги. Таким образом, создадим красивую траекторию движения тел.
Конструктор принимает три аргумента:
На данном этапе наш класс отображения выглядит так:
Напишем метод, который рисует траекторию движения. Он будет принимать два аргумента, а именно положения x и y движущегося тела. Первое, что нужно сделать, это сохранить новую позицию в массиве positions и отбросить всё лишние, хранящиеся в нём. Затем надо перебрать этот массив и нарисовать круг для каждой позиции. Но это по-прежнему выглядит не очень.
Визуализация симуляции
Напишем несколько canvas-шаблонов и свяжем их вместе с гравитационным N-объектным алгоритмом и траекториями движения, чтобы получить анимацию нашей Солнечной системы.
Прежде чем продолжить, вот HTML-код для симулятора:
Теперь перейдём к части JavaScript. Для начала нужна ссылка на canvas-элемент, после чего получаем его контекст рисования. Далее устанавливаем размеры. В данном примере установим свойства width и height canvas-элемента равными ширине и высоте окна браузера соответственно.
На данном этапе объявим некоторые константы для анимации:
Достаточно настроек. Вдохнём немного жизни в симуляцию, написав метод, который с помощью requestAnimationFrame API будет выполнять 60 шагов моделирования в секунду и анимировать движения тел.
Первое, что делает этот метод — продвигает симуляцию на один шаг. Это происходит путём обновления векторов положения, ускорения и скорости тел. Затем выполняется подготовка элемента canvas для следующего цикла анимации (очистка от нарисованных в предыдущем цикле анимации элементов с помощью метода clearRect() ).
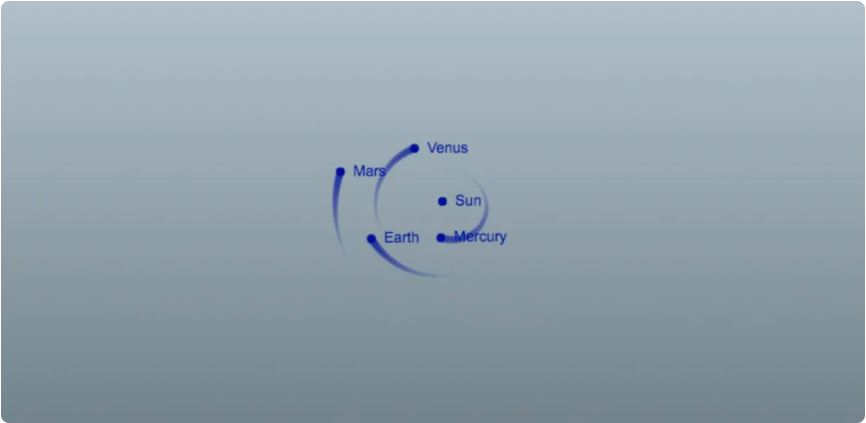
Теперь симулятор ожил. Тела представлены маленькими синими кругами с траекториями движения. Но ещё не реализован механизм добавления пользователем собственных тел с помощью мыши.
Добавление небесных тел в симуляцию
Ограничение симуляции
Если тело находится вне области просмотра на оси x, обращаем его вектор скорости так, чтобы он возвращался обратно в область просмотра. Аналогично для оси y. При этих двух условиях метод animate() будет выглядеть так:
Заключение
Люди склонны думать об орбитальной механике, как о чём-то, находящемся за пределами их понимания. Правда в том, что эта механика следует очень простому и элегантному набору правил. Немного JavaScript, математики и физики из средней школы, и вы смогли реконструировать внутреннюю часть Солнечной системы с довольно неплохой точностью. С помощью этого симулятора вы можете ответить на вопросы типа: «Что произошло, если бы появилась звезда с массой Солнца в нашей солнечной системе?», — или больше узнать о взаимосвязи между расстоянием тела от Солнца и его скоростью.
Если вам понравился этот материал и вы хотите посмотреть больше проектов по космосу и физике, загляните в этот репозиторий, а также посмотрите проект «Гармония сфер».
Гравитация, или На чём держится мир
Гравитация — это сила, которая действует на каждого обитателя Земли, впрочем, как и на саму Землю. Утрируя, можно сказать, текущий вид Вселенной существует благодаря силе притяжения. А значит пора разобраться, что такое гравитация простыми словами.
Определение гравитации
Слово «гравитация» происходит от латинского gravitas — вес.
Гравитация — сила, с помощью которой планета или другое тело притягивает объекты к своему центру. Именно благодаря ей мы не улетаем в космос, всегда притягиваясь к Земле. Так и планеты Солнечной системы всегда испытывают притяжение звезды и остаются на своих местах.
Как работает гравитация
Сила притяжения зависит от массы объектов и расстояния межу ними. Все, что имеет массу, имеет и гравитацию. Объекты с большей массой имеют большую гравитацию. Она ослабевает с расстоянием, и чем ближе объекты друг к другу, тем сильнее их тяготение.
Исаак Ньютон был первым, кто математически описал гравитацию и то, что она одинаково действует на все объекты во Вселенной: от падающего яблока до планет, которые движутся вокруг звезды. Так и появился закон всемирного тяготения, которого придерживались веками.
Сила притяжения F между двумя материальными точками с массами 


Здесь 
Кстати, падение яблока на голову Ньютона — это миф. Он действительно любил отдыхать под яблоней, и наблюдения за падающими яблоками натолкнуло его на мысль о всемирном тяготении. Но по голове Ньютона ничего не било.
Теория Ньютона объясняла гравитацию как некую силу. Но в последствии появилась теория Эйнштейна, в основе которой подход геометрический. Если простыми словами: крупные объекты искривляют пространство-время вокруг себя, а в это «искривление» попадают другие объекты.
Этот принцип хорошо показан в этом ролике:
Теория Энштейна — является действующей на сегодня.
Насколько важна гравитация?
Очень важна! Гравитация — это одна из сил фундаментальных взаимодействий, которым подчиняется всё, что есть во Вселенной. Вот эти взаимодействия:
Именно благодаря им мир такой, каким мы его знаем. Гравитация в этом списке является самым крупномасштабным, но одновременно и самым слабым взаимодействием, остальные — определяют взаимодействия на уровне частиц.
Как гравитация повлияла на Вселенную
Именно сила притяжение создает звезды и планеты, собирая вместе материал, из которого они сделаны. Гравитация — это то, что удерживает планеты на орбите вокруг Солнца и то, что удерживает Луну на орбите вокруг Земли.
Роль гравитации для землян
Те условия, в которых мы живём, были бы невозможны без неё. Она удерживает нашу планету на одинаковом расстоянии от Солнца, не позволяет атмосфере покинуть пределы Земли, как и всему, что находится на её поверхности. Гравитационное притяжение Луны притягивает к себе моря, вызывая приливы океана.

Гравитация очень важна для нас. Мы не могли бы жить на Земле без неё. Тяготение Солнца удерживает Землю на орбите вокруг него на постоянном комфортном для жизни расстоянии. Сила притяжения удерживает нашу атмосферу и воздух, которым мы дышим.
Гравитация — это то, что скрепляет наш мир.
Однако гравитация не везде одинакова на Земле. Она немного сильнее в местах с большей массой под землей, чем в местах с меньшей массой.
Есть ли гравитация у человека?
У каждого материального объекта есть своя сила притяжения, и человек не является исключением.
О выходе новых статей рассказываем в соцсетях
Интерактивное демо показывает, что гравитация — не сила, а искривление пространства-времени
Разработчик Тим Хаттон из Microsoft выпустил демо гравитации в соответствии с Общей теорией относительности, в которой гравитация не является обычной силой или полем, а представляет собой искривление пространства-времени.
Все тела в таком искривлении движутся по прямой. Например, параболическое движение брошенного тела в гравитационном поле Земли — своеобразная иллюзия, которая возникает для внешнего наблюдателя, а на самом деле тело движется по прямой.
Согласно ОТО, любое массивное тело создаёт своеобразную воронку в пространстве-времени. Пролетающие мимо тела изменяют свою траекторию согласно изгибам искривлённого пространства.
С точки зрения движущихся тел они продолжают перемещаться по прямой. Просто они попали в искривлённое пространство и не осознают, что для постороннего наблюдателя демонстрируют непрямолинейную траекторию.
Нужно обратить внимание, что в такой ситуации искривляются четыре измерения, в том числе и время.
Для фотонов света понятие времени не существует, поскольку они движутся точно со скоростью света, то есть начинают и заканчивают движение в один момент времени, а все расстояния по направлению движения сокращаются до точки (см. «Как фотоны воспринимают время?»).
В системе на интерактивном демо есть только одно пространственное измерение, показанное на вертикальной оси и обозначенное метрами. Измерение времени — это горизонтальная ось, обозначенная в секундах. Гравитационное поле постоянно в пределах интересующей нас области.
Используйте первый ползунок, чтобы изменить ускорение в системе отсчёта. Когда у системы отсчёта нулевое ускорение, она называется инерциальной системой отсчёта (ИСО).
Второй ползунок перемещает временное окно. При этом все траектории остаются прямыми линиями в инерциальной системе отсчета.
На интерактивных диаграммах можно перетащить начальное и конечное положение каждого объекта, чтобы изменить его траекторию. Однако все траектории свободного падения в инерциальной системе отсчёта являются прямыми линиями.
Искусственная гравитация перестаёт быть фантастикой
Искусственная гравитация давно была описана в фантастических романах и показана в фильмах вроде «Космической одиссеи 2001 года». Теоретически возможность создания искусственной гравитации не отрицается. Однако до проектов, которые можно было бы протестировать в условиях космических станций в ближайшее время, дело практически не доходило. Но совсем скоро все может измениться благодаря стараниям команды CU Boulder.
Зачем нужна искусственная гравитация
На самом деле тут все довольно просто и суть заключена в человеческой физиологии. Дело в том, что наши тела устроены таким образом, чтобы существовать, когда на все наши внутренние органы и костно-мышечный аппарат действует сила притяжения. В условиях космических станций этого воздействия, как вы понимаете, практически нет, что в перспективе чревато возникновением различных проблем со здоровьем. И если мускулатуру и суставы можно поддерживать в тонусе, занимаясь на специальных тренажерах, то вот внутренние органы таким образом не «потренируешь».
«Астронавты испытывают потерю костной и мышечной массы, сильную нагрузку на сердечно-сосудистую систему и имеют массу других рисков», — говорит Торин Кларк, один из руководителей CU Boulder. » Конечно, есть ряд упражнений и мер по поддержанию здоровья космонавтов, но искусственная гравитация помогла бы решить все проблемы разом.»
Как устроена установка по созданию искусственной гравитации
Сами разработчики называют машину «центрифугой с коротким радиусом действия». Установка представляет собой металлическую платформу, похожую на больничную каталку. На нее ложится человек, после чего платформа начинает вращаться. Сначала она вращается медленно, со временем набирая обороты.
«Угловая скорость, создаваемая центрифугой, толкает тело к основанию платформы. Это почти то же самое, как если бы вы стояли на земле.» — объяснил принцип действия господин Кларк.
При этом в ходе разработки инженеры столкнулись с весьма очевидной проблемой: при долгом вращении человека начинает тошнить. Можно ли избавиться от такого побочного эффекта? Как выяснилось, можно. Во время испытаний к 10 сеансу все испытуемые комфортно вращались в центрифуге, не испытывая никаких проблем. Скорость вращения при этом составляла 17 оборотов в минуту.
Почему нельзя использовать установку прямо сейчас
Прежде, чем приступать к полномасштабным испытаниям в космосе, ученым нужно ответить на ряд вопросов. А именно, надолго ли закрепляется эффект от обучения нахождению в центрифуге, не имеет ли такой подход отдаленных последствий для здоровья и, самое главное, как долго астронавту нужно принимать это «гравитационную ванну» для того, чтобы компенсировать все негативные последствия невесомости. Как только целесообразность и безопасность подхода, разработанного командой CU Boulder, будет доказана, можно будет ожидать появления первой рабочей установки по созданию искусственной гравитации в условиях космоса.
Обсудить эту и другие новости вы можете в нашем чате в Телеграм.