Для чего нужна кинематика
Кинематика Что это вообще такое, и зачем это нужно?
Раздел школьной механики про движение состоит из трёх основных частей: кинематики, динамики и статики.
Проще всего это объяснить так. Например, ты идёшь по улице, и вдруг на пути появляется яма. Не заметив её, ты падаешь. Говоря умным словом – движешься.
И все эти три раздела смотрят на это движение каждый со своей стороны.
Так вот. Кинематика – это:
Как ты движешься? (Вниз, ускоряясь.) Когда остановишься? (Когда долетишь до дна.) Через какое расстояние остановишься? (Ровнёхонько глубина ямы, ну и углубление, оставленное туловищем, если хорошо упадёшь.)
Динамика – это: почему ты начал двигаться, почему продолжаешь это делать и почему закончил (если закончил). Например: начал потому, что это сила притяжения Земли к тебе такая вредная, и продолжаешь лететь, потому что она по-прежнему действует.
А статика – это что надо делать, чтобы ты оставался в равновесии. То есть когда занёс одну ногу над ямой, надо было успеть сообразить, что делаешь, и убрать её обратно, и в то же время податься туловищем немного назад.
Говоря чуть более умным языком: кинематика как бы отвечает на вопрос «как тело движется?», динамика – «почему тело движется?», а статика – «при каких условиях тело будет в равновесии?».
Кругом умное слово: движение. Оказывается, и это тоже понятие! Причём оно настолько заумное, что означает всего-навсего изменение. Просто изменение, и всё. В широком смысле – то есть в физике вообще. Если брать более узко, то механическое движение – это когда что-то меняет своё положение.
Но есть один подкол. Вспомним детство: едем на машине, автобусе, электричке… это не так важно, – и смотрим в окно. И кажется, будто дома или деревья едут мимо тебя, а ты стоишь на месте. А вот если на тебя посмотрит кот из окна первого этажа дома (мимо которого проезжаешь) – ему будет казаться, что ты движешься.
Короче, суть всей этой маленькой шизофрении – движением можно считать что-то, только если это движется относительно чего-то.
Нет, это ещё не страшная теория относительности Эйнштейна, не надо пугаться. Обзывается сие хозяйство «системой отсчёта». Вот поставил на себе жирную белую точку мелом – всё, теперь считаешь себя точкой с координатами (0;0;0). А тот момент, когда поставил точку – это считаешь, что пошло время (с 0 секунд и до бесконечности… плюс бесконечности – для особых умников). Всё, теперь ты – система отсчёта! Относительно тебя, например, крутятся Земля и другие планеты. Ну прямо центр Вселенной!
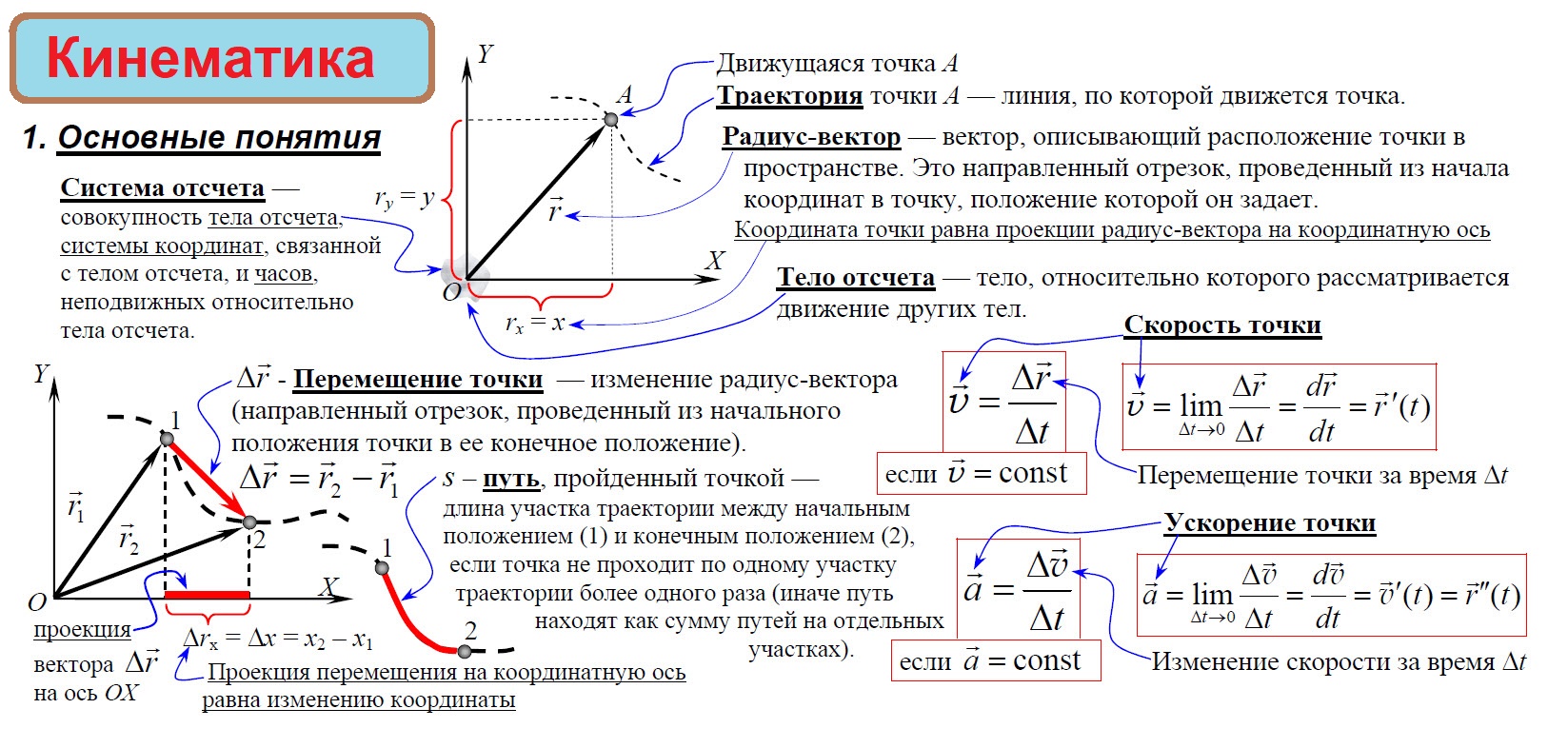
Вкратце и поумнее: для положения тела необходимо определить систему отсчёта (это «отправная» точка с координатами (0;0;0) и начало отсчёта времени), относительно которой будет считаться всё, что связано с тем, как оно движется. Если относительно данной системы отсчёта тело меняет своё положение, то считаем, что оно двигается.
Данный текст является ознакомительным фрагментом.
Для чего нужна кинематика
Механическое движение – изменение положения тела относительно других тел с течением времени. Способы описания: словесный, табличный, графический, формулами.
Материальная точка – тело, собственными размерами которого в данных условиях можно пренебречь.
Траектория – линия, которую описывает материальная точка при своём движении в пространстве. По виду траектории все движения делятся на прямолинейные и криволинейные.
Система отсчёта – часы и система координат, связанные с условно выбираемым телом отсчёта (наблюдателем).
Относительность движения – различие скорости, направления и траектории движения в различных системах отсчёта.
Перемещение – вектор, проведённый из начального положения материальной точки в её конечное положение.
Типы движений
1. Равномерное движение
1.1. Равномерное прямолинейное движение
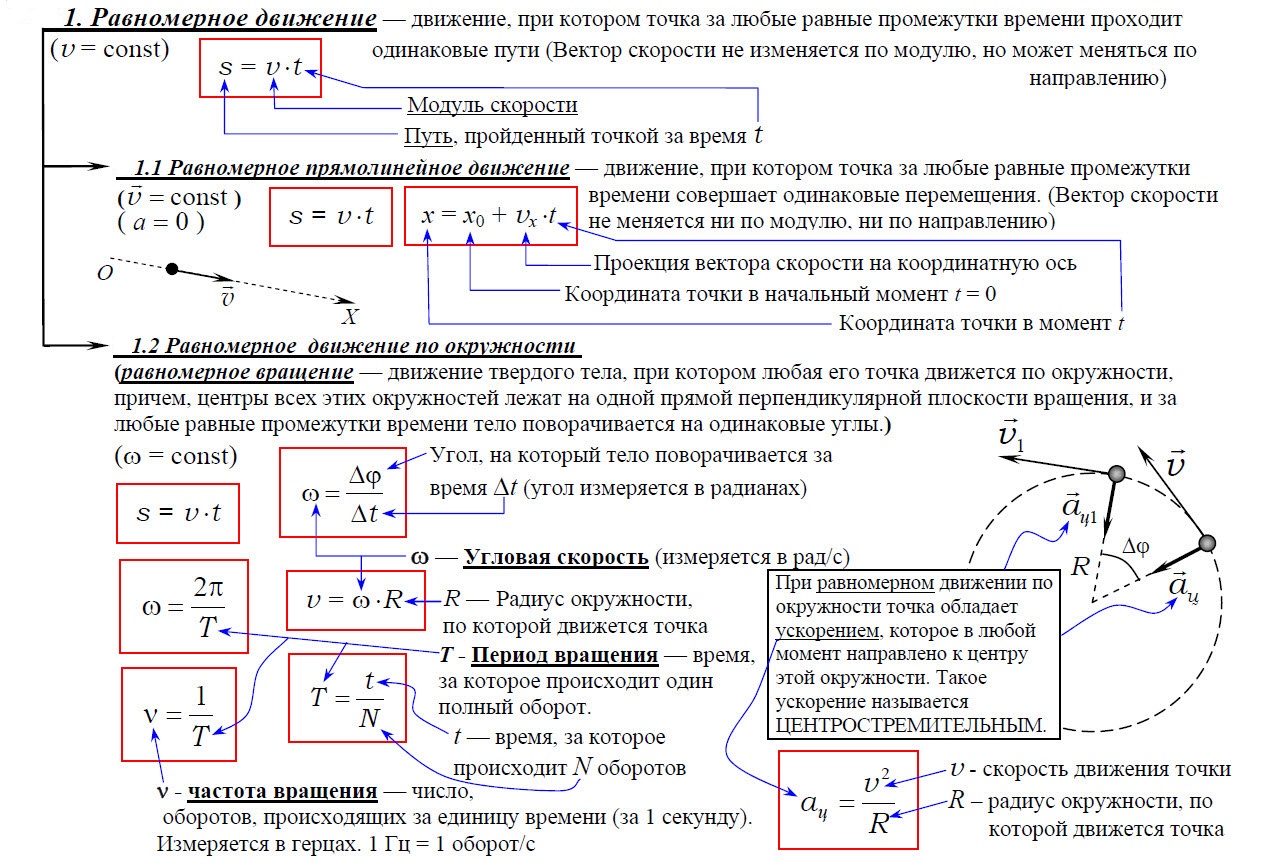
Равномерное движение – движение тела, при котором за равные интервалы времени оно преодолевает равные части пути.
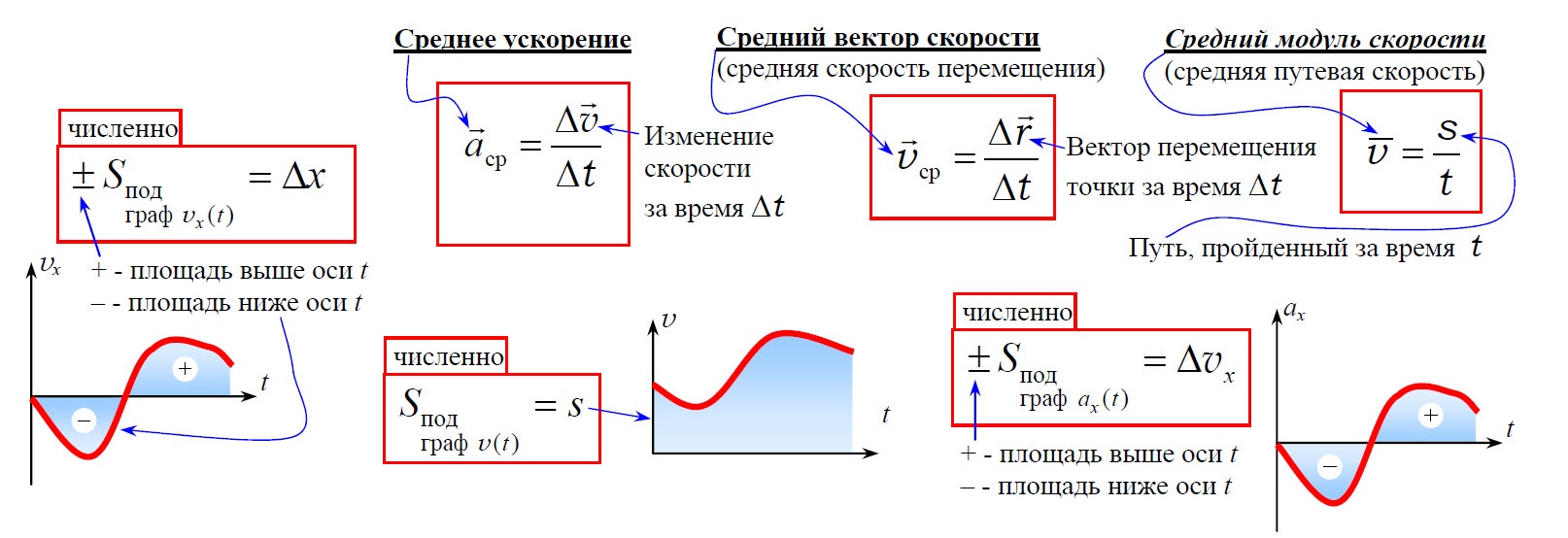
Скорость равномерного движения равна отношению пройденного пути к интервалу времени, за который этот путь пройден.
Скорость равномерного прямолинейного движения равна отношению перемещения к интервалу времени его совершения.
Уравнение равно-прямолинейного движения x = x o + υ ox t показывает, что координата линейно зависит от времени.
Мгновенная скорость равна отношению перемещения к бесконечно малому интервалу времени, за который оно произошло.
1.2 Равномерное движение по окружности (равномерное вращение)
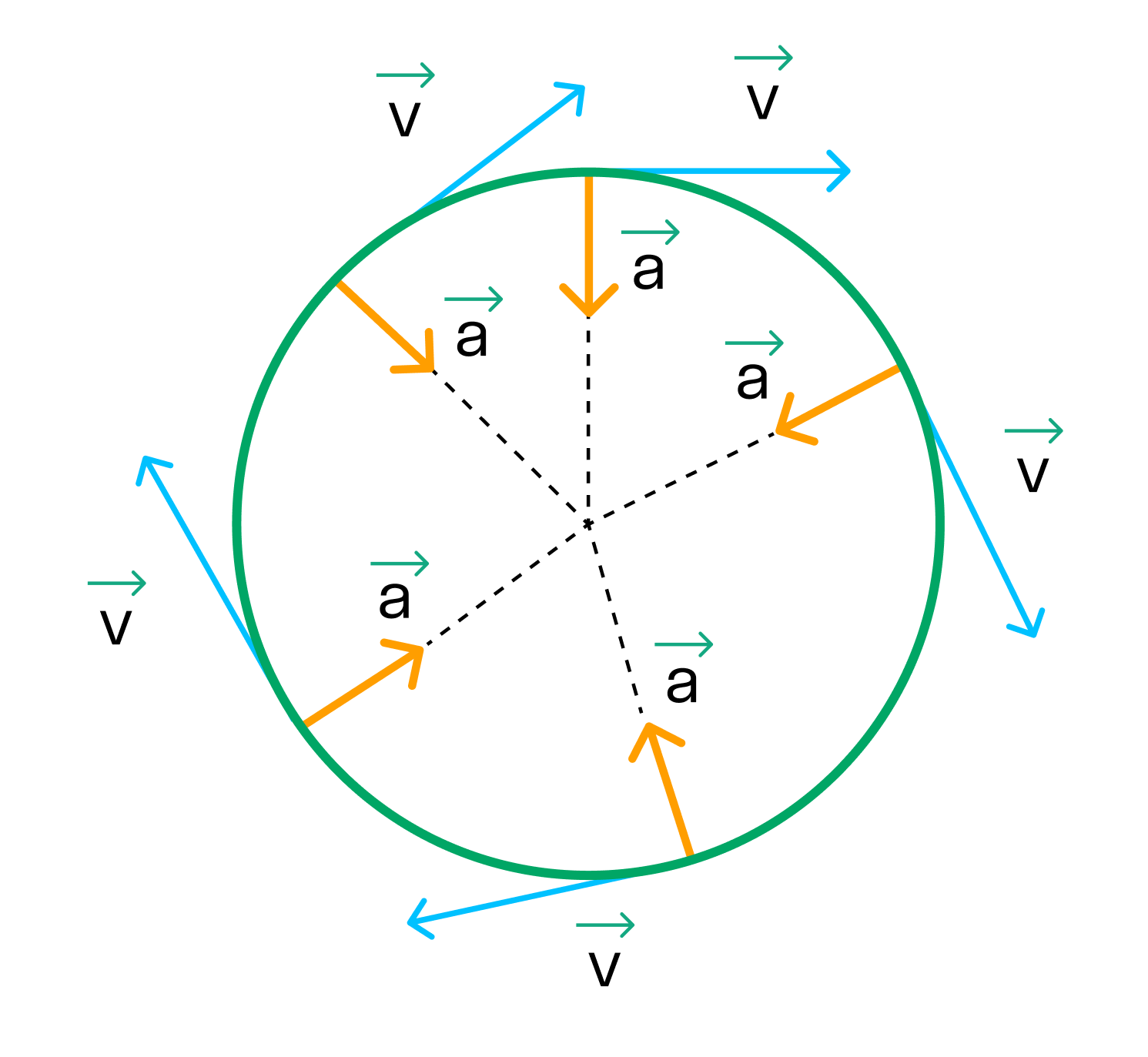
Равномерное движение по окружности — это движение, при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности.
Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.
2. Движение с постоянным ускорением
Равноускоренное движение – движение, при котором мгновенная скорость за любые равные интервалы времени меняется одинаково.
Мгновенное ускорение равно отношению изменения мгновенной скорости тела к бесконечно малому интервалу времени, за который это изменение произошло.
Ускорение равноускоренного движения равно отношению изменения мгновенной скорости тела к интервалу времени, за который это изменение произошло.
Уравнение равноускоренного движения y = yo + υoyt + ½ay t² показывает, что координата квадратично зависит от времени. Уравнение υy = υoy + ay t показывает, что скорость линейно зависит от времени.
Центростремительное ускорение – ускорение, всегда направленное к центру окружности при равномерном движении по ней материальной точки. Модуль центростремительного ускорения равен отношению квадрата модуля скорости равномерного движения по окружности к её радиусу.
Основные определения кинематики
Зачем знать основные определения кинематики?
Почему этот раздел очень важен?
Как он поможет тебе на экзамене?
Все очень просто. В этом разделе мы «дадим имена самым важным вещам».
Тебе в детстве сказали, что вот это стул и на нем сидят, а вот это стол, на нем едят? Сказали. И после этого ты сидишь на стуле, а ешь за столом. Ну чаще всего 🙂
Так и здесь. Все, о чем мы будем говорить на этом уроке, нужно, чтобы мы говорили на одном языке.
И чтобы на экзамене ты не перепутал, например, траекторию, путь и перемещение.
Основные определения кинематики
Что ты вспоминаешь при слове «движение»?
Слова учителя физкультуры: «Движение – это жизнь, ребята»? Движение за права человека? Или ту задачку по математике, где пришлось складывать скорости?
Все это означает какие-то изменения. Экологическое движение меняет мир, очищая его. Спорт меняет наше тело. А мы в свою очередь можем изменить свое положение в пространстве, сходив погулять.
Все это и есть движение. Но это понятие очень широкое. Давайте сузим его и определим, а что такое механическое движение?
Что такое механическое движение?
Мы говорили, что движение – это всегда какое-то изменение. Но что меняется при механическом движении?
Ты можешь сказать: «Меняется положение тела». Хорошо, это действительно так.
Но давай представим, что мы сидим в купе поезда, который мчится из Москвы во Владивосток.
Движемся мы или нет? А движется ли поезд?
Кажется, очень легко дать ответы на эти вопросы, потому что и мы вместе с поездом движемся. Но если ты посмотришь на соседей по купе, а они посмотрят на тебя, то никаких изменений (никакого движения) вы не увидите.
Дело в том, что все зависит от точки отсчета.
Так, например, если за точку отсчета взять поезд, то ни мы ни наши соседи по купе относительно поезда двигаться не будем. И поезд не будет двигаться относительно нас.
А вот люди, стоящие на перроне, относительно поезда движутся. И поезд движется относительно них.
Значит для того, чтобы сказать движется тело или нет, нам нужно определить точку отсчета.
Точка отсчета – тело, относительно которого мы рассматриваем движение.
Любое движение происходит с течением времени. Если бы не было времени, ничего бы не менялось и не было бы никакого движения.
Значит для того, чтобы было механическое движение, нам нужно чтобы изменялось время.
Механическое движение – это изменение положения тела в пространстве относительно других тел с течением времени.
В чем состоит основная задача механики?
Ты абсолютно прав, движение бывает очень разным!
Основная задача механики – указать положение тела в пространстве в любой момент времени, не только в настоящем, но и в будущем.
То есть уметь предсказывать его!
Если мы хотим знать почему тело движется, мы обращаемся к разделу механики, который называется динамикой. Но пока, чтобы не усложнять все сразу, мы не будем интересоваться причинами движения тела…
Если нам не интересна причина движения тела, мы обращаемся к разделу механики, который называется кинематикой.
Что такое кинематика?
Кинематика – это раздел механики, который изучает движение тела, не рассматривая причину этого движения.
Она просто описывает движение тела, но не объясняет его.
Движение – изменение положения тела в пространстве с течением времени.
Но тело состоит из множества точек. Неужели придется описывать движение каждой из них? Будет, наверное, трудно…
Вовсе нет! Есть два способа облегчить себе эту задачу.
Первый способ. Если все точки тела движутся одинаково, почему бы не рассмотреть движение лишь одной из них?
Такое движение, при котором все точки тела движутся одинаково, называется поступательным движением.
Что такое поступательное движение?
Соединим прямой любые две точки тела. Когда тело движется поступательно, эта прямая будет параллельна каждому своему положению в любой момент времени. Наверное, это трудно представить, но вот тебе рисунок:
Видишь, прямая a параллельна прямой b, и они обе параллельны прямой c.
Записывается это так: \(a\parallel b\parallel c\)
И, соответственно, еще одно определение поступательного движения:
Поступательное движение – то, при котором любая прямая, соединяющая две любых точки тела, остается параллельна своему начальному положению в любой момент времени.
Слово «любая» здесь важно. Потому что если в теле найдется хотя бы одна прямая, соединяющая две любых его точки, которая не будет параллельна самой себе при движении, то такое движение не будет считаться поступательным.
Хорошо, с поступательным движением разобрались. А есть ли еще какое-нибудь движение? Что если наш треугольник, перевернуть, сделать из него юлу и раскрутить ее? Будет ли в этом случае тело двигаться поступательно?
Нет. Потому что, например, грань юлы не будет параллельна самой себе во время движения. Тогда какое это движение?
Это вращательное движение.
Что такое вращательное движение?
Что общего у колеса и нашей планеты? Точки этих тел вращаются вокруг прямой по разным окружностям.
И эта прямая называется осью вращения. А такое движение называется вращательным.
Вращательное движение – это такое движение тела, при котором все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
И, кстати, ось вращения не обязательно должна проходить через центр тела. Например, когда вы крутите ключи от машины вокруг пальца, ось вращения проходит через кольцо, на котором висят ключи, а не через центр ключей.
И вот что интересно…
Даже самое сложное движение можно описать комбинацией поступательного и вращательного!
Вернемся к тому моменту, когда мы сидели в купе движущегося поезда. Представь, что в твоих руках чашка с чаем и ты размешиваешь в нем кубик сахара. Он будет вращаться вокруг своей оси (вращательное движение) и при этом двигаться вместе с поездом относительно деревьев за окнами (поступательное движение).
Что такое материальная точка и зачем она нужна?
Земля, вращаясь вокруг Солнца, к тому же вращается вокруг своей оси. И все их точки движутся по-разному. Что в этом случае делать? Чтобы ответить на этот вопрос, нужно понять, действительно ли нам это важно.
Если по реке плывут лодка с парусами и яхта, будем ли мы описывать движение всех их точек?
Нам не важны их размеры и формы и движение всех точек этих тел. Но нам важно, например, время, за которое они преодолеют определенное расстояние.
Парусник и яхта – тела, размерами которых в данной задаче можно пренебречь.
Такие тела называются материальными точками.
Следует помнить, что пренебречь их размерами и формой можно не всегда. Так, например, если в задаче необходимо выяснить, смогут ли они пройти через узкое место в реке, их размеры имеют огромное значение!
Решая задачи по кинематике, будем считать тела материальными точками, если условия задачи не требуют другого.
Материальной точкой называется тело, размерами которого В ДАННОЙ ЗАДАЧЕ можно пренебречь.
С этого момента для того чтобы решить основную задачу механики, определить тело в пространстве в любой момент времени мы будем оперировать не всем телом, а ТОЧКОЙ!
Если задача не требует другого – важная оговорка!
Мы можем рассмотреть движение точки в любой момент времени, спрогнозировать положение в будущем и так далее.
Но что для этого необходимо?
Прежде всего понять, что положение тела можно задать числами. И вы наверняка знаете, как они называются…
Координаты тела и положение тела на прямой, плоскости и в пространстве
Как думаете, что связывает дороги, шахматы и спрятанные сокровища?
Координаты.
Координаты — это числа, с помощью которых задается положение материальной точки в пространстве.
Сколько чисел нам нужно, чтобы задать координаты материальной точки? Одно? Два? Три? Давайте разберемся.
Допустим мы заблудились в лесу, долго блуждали и в конце концов вышли на дорогу, где стоит столбик с цифрой «25». Как мы вызовем помощь? Мы позвоним и скажем: «Я нахожусь на 25 километре такого-то шоссе!»
Шоссе – это прямая (ну почти). Значит, чтобы задать координаты на прямой нам достаточно одного числа.
А сколько чисел нам нужно чтобы понять где находится шахматная фигура?
Позиция фигуры в шахматах задается двумя числами, например, Е6 («Е» можно заменить числом). Так мы определяем координаты на плоскости.
На уроке географии, когда мы только начинаем учиться работать с картой, мы определяем координаты географических объектов и нам тоже требуются два числа: широта и долгота.
А вот если мы захотим найти клад, нам потребуются три числа, одно из которых – глубина. Нам важно, насколько глубоко копать.
Так мы определяем положение тела в трехмерном пространстве. Мы с вами живем в таком трехмерном пространстве. У нас трехмерная система координат.
Система координат – это способ определять положение тела в пространстве с помощью чисел.
Давай подытожим. Вырисовывается некоторая система, которая позволяет нам определить положение тела.
Система отсчета или три вещи, необходимые для определения движения
Время
Можем ли мы двигаться вне времени? Движение вне времени невозможно. И значит, его нужно его как-то измерить. У нас должны быть часы или что-то в этом роде для измерения времени.
Тело отсчета
Можем ли мы двигаться сами по себе? Нет. Мы всегда движемся относительно чего-то. И, соответственно, нам нужно что-то, относительно чего мы начнем отсчет движения.
И это что-то называется телом отсчета.
Система координат
Когда мы решаем задачу по механике мы должны определиться в какой системе координат мы будем определять положение точки с помощью чисел.
Система отчета
Таким образом, для определения движения нам нужны три вещи:
В совокупности они образуют систему отсчета.
Система отсчёта — это совокупность неподвижных относительно друг друга тел (тело отсчёта) в связанной с ними системе координат, и отсчитывающих время часов (прибор), по отношению к которой рассматривается движение каких-либо тел.
Для одной и той же ситуации можно выбрать множество разных систем отсчета. В зависимости от этого мы либо упрощаем, либо усложняем себе задачу.
Во времена Коперника люди считали, что Солнце движется вокруг Земли. Ведь Земля относительно нас неподвижна, верно? А солнце восходит и заходит. Поэтому нам кажется, что солнце движется вокруг нас.
Но Коперник немного подумал (ну как немного :)) и поменял систему отсчета! Гипотеза Коперника о том, что это мы вращаемся вокруг Солнца, объяснила множество вещей.
Перемещение. Траектория. Путь.
Перейдем еще ближе к задачам. Пусть некоторая материальная точка двигалась из пункта А в пункт В.
Давай нарисуем это. А чтобы было понятно куда двигалась эта материальная точка, давай обозначим направление движения стрелкой!
Но что есть стрелка?
Это ведь направленный отрезок, то есть вектор. Иными словами, движение – это всегда вектор! Об этом нужно всегда помнить. Нам все время нужно указывать, куда направлено движение.
Этот вектор связывает начальное и конечное положение точки и называется перемещением тела. На рисунке перемещение обозначено как \(vec\).
Перемещением называется вектор, проведенный из начального положения тела в конечное.
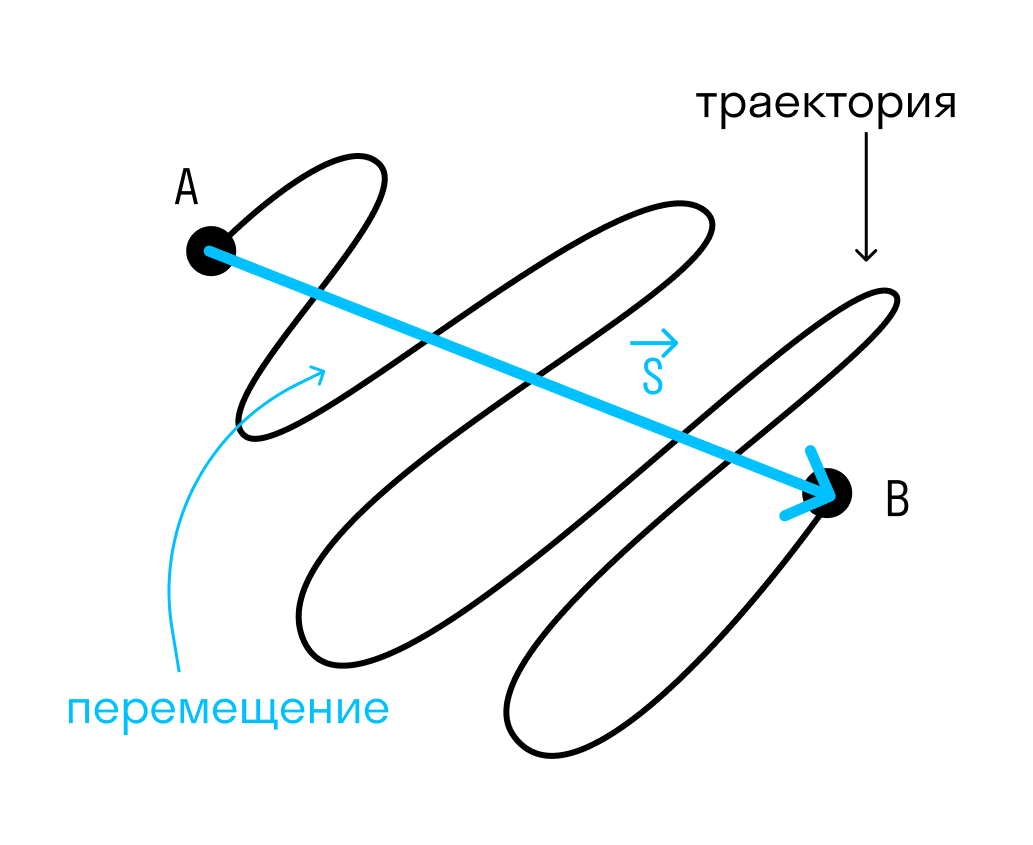
Как много идеально прямых дорог между городами ты видел в своей жизни? Могу поспорить, что ни одной. Если тело оказалось из пункта А в пункте В, оно вовсе не обязательно двигалось по прямой. Тело могло двигаться по кривой или ломаной линии.
Линия, по которой движется тело – это траектория.
А длина траектории – это путь.
Перемещение – это всегда вектор, а путь – это всегда число! Запомните это.
Путь всегда больше или равен модулю вектора перемещения:
Почему мы говорим «модулю вектора перемещения», а не просто «вектору перемещения»? Потому что мы не можем сравнивать белое и горячее. Мы не можем сравнить вектор (перемещение) с числом (путь).
Но мы можем сравнить число с числом. Для этого мы «делаем» из вектора число, заключив его под знак модуля. Это число есть длина вектора. А длина вектора — его модуль.
Самый короткий путь совпадает с перемещением, то есть это прямая. В этом случае они равны.
А может ли перемещение быть равно нулю?
Попробуем это представить…
Но это вовсе не значит, что мы будем бежать на месте!
Мы можем выбежать на улицу, пробежать через парк, но как только вернемся домой, наше перемещение станет равным нулю, ведь мы оказались в том же месте, откуда и начинали движение. Путь, однако, нулю не равен.
Таким образом, мы разобрали основные понятия кинематики. Успешное решение задач напрямую зависит от понимания того, с чем мы работаем и что пытаемся найти. Поэтому давайте еще раз выпишем все определения.
Кинематика
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч и у вас нет никаких препятствий на пути, то вы скорее всего будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
Векторные величины (определяются значением и направлением)
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики. Скорость — это векторная физическая величина, характеризующая быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
→ →
V = S/t
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
В чем разница между перемещением и путем?
Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уравнение движения
Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) = x0 + vxt
x(t) — искомая координата [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v