Для чего нужна логарифмическая шкала

Что такое логарифмическая линейка и как ей правильно пользоваться

Логарифмическая линейка — это универсальный счетный прибор, который применялся для умножения, деления, возведения в квадрат и куб, вычисления квадратных и кубических корней, синусов, тангенсов и других значений. До появления калькуляторов, компьютеров и смартфонов инженеры носили логарифмические линейки на поясе, а линейка «Pickett» даже полетела на Луну вместе с космонавтами.

Уильям Отред — изобретатель логарифмической линейки

Уильям Отред, выпускник Итонской школы и Кембриджского королевского колледжа, пастор церкви в Олсбери в графстве Суррей, был страстным математиком и с удовольствием преподавал любимый предмет многочисленным ученикам, с которых не брал никакой платы. «Маленького роста, черноволосый и черноглазый, с проницательным взглядом, он постоянно что-то обдумывал, чертил какие-то линии и диаграммы в пыли, — так описывал Отреда один из биографов. — Когда ему попадалась особенно интересная математическая задача, бывало, что он не спал и не ел, пока не находил ее решения». Он является первым изобретателем логарифмической линейки.

История изобретения

В 1631 году Отред опубликовал главный труд своей жизни — учебник Clavis Mathematicae («Ключ математики»), выдержавший несколько переизданий на протяжении почти двух веков. Однажды, обсуждая «механические вычисления» с помощью линейки Гюнтера со своим учеником Уильямом Форстером, Отред отметил несовершенство этого метода. Между делом учитель продемонстрировал свое изобретение — несколько концентрических колец с нанесенными на них логарифмическими шкалами и двумя стрелками.

Форстер был восхищен и позднее писал: «Это превосходило любой из инструментов, которые были мне известны. Я удивлялся, почему он скрывал это полезнейшее изобретение многие годы. » Сам Отред говорил, что он «просто изогнул и свернул шкалу Гюнтера в кольцо», и к тому же был уверен, что «настоящее искусство [математики] не нуждается в инструментах. », их использование он считал допустимым только после овладения этим искусством. Однако ученик настоял на публикации, и в 1632 году Отред написал (на латыни), а Форстер перевел на английский брошюру «Круги пропорций и горизонтальный инструмент», где была описана логарифмическая линейка.

Споры об авторстве

Логарифмическая линейка значительно облегчила сложные вычисления для инженеров и ученых. В XX веке до появления калькуляторов и компьютеров логарифмическая линейка была таким же символом инженерных специальностей, каким для врачей является фонендоскоп.

Как пользоваться логарифмической линейкой

Рассмотрим, как проводить базовые математические операции с помощью логарифмической линейки. Принцип ее действия основан на том, что умножение и деление чисел заменяется соответственно сложением и вычитанием их логарифмов.

1. Сложение

Представим, что нам нужно найти сумму двух и четырех. На одной линейке (нижней) откладываем два деления (на рисунке отрезок а), вторую линейку (верхнюю) сдвигаем вправо на эти же два деления, после чего откладываем на ней еще четыре деления (отрезок b на рисунке). Смотрим на нижней линейке, над каким числом находится точка, в которую мы пришли — это шесть.

2. Умножение

Для начала введем переменные: a ∙ b = с при a = 2, b = 3. Затем возведем в логарифм обе части равенства и получим Lg(a) + lg(b )= lg(с). Взяв две линейки с логарифмическими шкалами, увидим, что сложение значений lg2 и lg3 дает в результате lg6, то есть произведение 2 на 3.

На основной шкале корпуса линейки (вторая снизу) выбираем первый сомножитель и на него устанавливаем начало основной, нижней, шкалы движка (она на лицевой стороне последнего и точно такая же, как основная шкала корпуса).

Затем на основной шкале движка волосок бегунка устанавливается на втором сомножителе. На основной шкале корпуса линейки под волоском смотрим ответ. Если при этом волосок выходит за пределы шкалы, то на первый сомножитель устанавливают не начало, а конец движка (с числом 10).

Источник

Логарифмическая шкала

На шкале в логарифмическом масштабе длина отрезка шкалы пропорциональна логарифму отношения величин отмеченных на концах этого отрезка (в то время как на шкале в линейном масштабе длина отрезка пропорциональна разности величин на его концах).

Наглядный пример употребления и полезности логарифмического масштаба — логарифмическая линейка которая позволяет проводить довольно сложные вычисления с точностью два-три десятичных знака.

Примеры применения логарифмического масштаба:

Смотреть что такое «Логарифмическая шкала» в других словарях:

ЛОГАРИФМИЧЕСКАЯ ШКАЛА — (logarithmic scale) Шкала на диаграмме, где единицей измерения выступает значение логарифма переменной. Логарифмические шкалы используются прежде всего в диаграммах, в которых на одной, обычно горизонтальной шкале показано время, а на… … Экономический словарь

логарифмическая шкала — Шкала, построенная на основе систем логарифмов. Примечание Для построения логарифмических шкал обычно используются системы десятичных или натуральных логарифмов, а также система логарифмов с основанием два. [МИ 2365 96] Тематики метрология,… … Справочник технического переводчика

логарифмическая шкала — 2.2.7 логарифмическая шкала : Шкала измерений, получаемая логарифмическим преобразованием измеряемой величины. Источник: РМГ 83 2007: Государственная система обеспечения единства измерений. Шкалы измерений. Термины и определения … Словарь-справочник терминов нормативно-технической документации

логарифмическая шкала — logaritminė skalė statusas T sritis automatika atitikmenys: angl. logarithmic scale vok. logarithmische Skala, f rus. логарифмическая шкала, f pranc. échelle logarithmique, f … Automatikos terminų žodynas

логарифмическая шкала — logaritminė skalė statusas T sritis Standartizacija ir metrologija apibrėžtis Logaritminiu masteliu sudaryta skalė. atitikmenys: angl. logarithmic scale vok. logarithmische Skala, f rus. логарифмическая шкала, f pranc. échelle logarithmique, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas

логарифмическая шкала — logaritminė skalė statusas T sritis fizika atitikmenys: angl. logarithmic scale vok. Logarithmenskala, f rus. логарифмическая шкала, f pranc. échelle logarithmique, f … Fizikos terminų žodynas

Логарифмическая шкала разностей — Логарифмическая шкала измерений, получаемая при логарифмическом преобразовании величины, описываемой шкалой отношений, или интервала в шкале разностей, т.е. шкала, определяемая зависимостью L = log (Х/Х0), где Х текущее, a X0 принятое по… … Словарь-справочник терминов нормативно-технической документации

логарифмическая шкала разностей — Логарифмическая шкала измерений, получаемая при логарифмическом преобразовании величины, описываемой шкалой отношений, или интервала в шкале разностей, т.е. шкала, определяемая зависимостью L = log (X/X0), где Х текущее, а Х0 принятое по… … Справочник технического переводчика

логарифмическая шкала для частот — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN logarithmic frequency scale … Справочник технического переводчика

Логарифмическая шкала времени — вид логарифмической шкалы, которая показывает наиболее значимые исторические события на одной странице в десяти строках в логарифическом масштабе.[источник не указан 448 дней] События далёкого прошлого имеют меньшее влияние на … Википедия

Источник

Почему я пользуюсь логарифмической шкалой при просмотре графика цены акций?

Вводная заметка о пользе логарифмов.

Думаю, все вы понимаете, что конкретная цена акции не имеет никакого значения. Главное, чтобы её цена была не выше той суммы, которую инвестор хочет потратить. Например, акция BRK.A стоит порядка 420к$, что явно переходит все границы разумного. Но в остальном, если вы хотите купить акции какой-то компании на условные сотню баксов, то вам, в принципе, всё равно, будет ли это десять акций по десять долларов или сотня акций по доллару.

Значение имеет то, на сколько процентов цена изменилась. То, что какая-то акция поднялась на доллар — ничего вам не говорит, если вы не знаете, какая у неё была прошлая стоимость, потому что 1+1 и 10+1 — это совершенно разные вещи. С другой стороны, если акция поднялась на 25%, то вам совершенно не обязательно знать, сколько она стоила раньше — вы и так получили всю нужную информацию.

Допустим теперь, что вы анализируете поведение акции за большой временной период — несколько лет или даже десятилетий. Если компания развивалась всё это время, то цены сейчас намного выше цен более раннего периода. Например, акция TSLA совсем недавно стоила 900$, а несколько лет назад она стоила всего лишь 50$:

Если мы посмотрим на график выше, то колебания цены мы увидим только начиная с 2020 года. А начиная с 2014 года и до 2020 идет чуть ли не прямая линия, как будто цена акции все эти годы стояла на месте. Почему так? Потому что на фоне колебаний цены между 900$ и 550$, колебания между 30$ и 70$ совершенно не видны. А ведь в процентах второй случай куда как значимей.

А еще падение с 180$ до 70$ в начале 2020 года в процентах примерно в полтора раза сильнее падения с 900$ до 550$ в начале 2021 года, но на графике более позднее событие выглядит куда как страшнее более раннего.

Получается, что такой график не просто теряет часть информации, но и вводит нас в заблуждение.

Тут на помощь приходит логарифмическая шкала. Преимущество такой шкалы в её нелинейности. Я не буду объяснять, что такое логарифм — это вы можете сами в Википедии почитать. Да и, как известно, каждая дополнительная формула в статье уменьшает количество её читателей в два раза 🙂

На графике выше — та же акция, с тем же временным промежутком, но только в логарифмическом представлении. Сравните с прошлым, линейным графиком, и убедитесь, насколько понятней выглядит поведение цены за весь период времени, а не только за последний год.

Вообще говоря, кванты и алготрейдеры вовсю используют логарифмы, чтобы избавиться от «шума» в данных. Если я когда-нибудь найду достаточно времени, чтобы обучать алготрейдингу, то мы еще вернемся к этой теме.

Самостоятельно поиграться с логарифмическим представлением цен можно, к примеру, на TradingView, в настройках графика.

Если то, что я пишу, вам кажется интересным — подписывайтесь на мой телеграм-канал, чтобы своевременно получать уведомления о новых постах:

Поскриптум: я не инвестиционный консультант и никогда им не был. Ничто из вышенаписанного не следует рассматривать как инвестиционную рекомендацию.

Источник

Логарифмическая шкала

Логарифмическая шкала особенно подходит для учета порядков величин в приложениях. Он показывает в небольшом пространстве широкий диапазон значений при условии, что они не равны нулю и имеют один и тот же знак.

Резюме

Определение

Логарифмический масштаб определяется только для строго положительных значений.

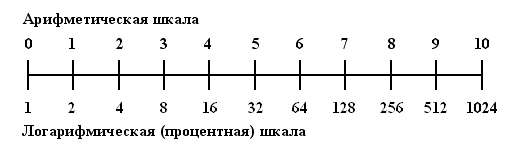
Сравнение линейной шкалы и логарифмической шкалы

На рисунке выше показаны два типа шкал:

В логарифмической шкале большие числа сжимаются, перемещаются ближе к 1 и легко представляются, в то время как числа меньше 1 расширяются и очень быстро возвращаются к отрицательной бесконечности.

Логарифмические единицы

Линейная шкала с логарифмической шкалой эквивалентна логарифмической шкале с точки зрения рассматриваемой величины.

Использовать

Конструкция лестницы

Мы знаем минимальное x _min и максимальное x _max значения, которые должны быть представлены, и длину l шкалы между этими двумя значениями.

Вместо того, чтобы вычислять это шаг за шагом, мы используем фундаментальное свойство логарифмов:

журнал ( a × b ) = журнал ( a ) + журнал ( b )

Мы хотим, чтобы были указаны числа, кратные 10. Для отношения 1000 есть три умножения на 10, что соответствует трем модулям длиной 600 ÷ 3 = 200 пикселей.

В этих модулях мы хотим указать расположение каждого значения от 2 до 9.

Каждый из модулей воспроизводится трижды, форма неизменна, меняется только легенда точек.

Примечание. Основание логарифма, по которому выполняются вычисления, не имеет значения.

Строительство без счетной машины

Источник

Reveal the Data

Выбор типа шкал для графика, всегда казалось мне интуитивно понятной задачей. Однако, когда мне нужно было объяснить, чем они отличаются, то я не смог привести понятных аргументов. В интернете хорошей информации мне не попалось. Поэтому решил разобраться, откуда растут ноги у разных видов шкал и как их следует применять. Я решил рассмотреть три самых распространенных вида шкал — равномерную, логарифмическую и степенную.

Равномерная шкала

Самый распространенный и привычный вид шкал. Также их называют арифметическими или линейными шкалами. На такой шкале значения равноудалены друг друг от друга.
Например значения 100 и 200, и 200 и 300 отстают друг от друга на одно и тоже расстояние.
Например, на этом графике по оси Y — равномерная шкала с шагом в 20 лет средней продолжительности жизни, а по оси X — равномерная шкала с шагом 10 календарных лет.

Логарифмическая шкала

Этот вид шкал тоже используется достаточно часто, особенно когда речь идёт о научных исследованиях. Она используется для отображения широко диапазона величин, когда значения, которые попадают на график отличаются на много порядков. То есть когда мы хотим одновременно видеть и значения 0.1, 0.2 и значения 100, 200 на одном графике. Зачастую это связанно с физикой процесса. Так, например, в музыке ноты, различающиеся по частоте в два раза это ноты на октаву выше (Ля и Ля следующей октавы). Чтобы показать частоты двух нот будет удобно использовать логарифмическую шкалу.

Но бывает, что в наборе данных просто содержаться большой разброс данных. Например, как на этом графике из Beautiful Evidence Тафти, где он использует логарифмические шкалы для сравнения массы тела и мозга различных существ. Так как бывают и крошечные рыбки и огромные киты, то на таком графике удобно использовать логарифмические шкалы.

Чаще всего используются логарифмические шкалы с основанием 10. Это значит, что одинаковые расстояние на графике откладываются между значениями отличающимися на один порядок. Но бывают логарифмические шкалы с другими основаниями. Например 2.

Степенная шкала

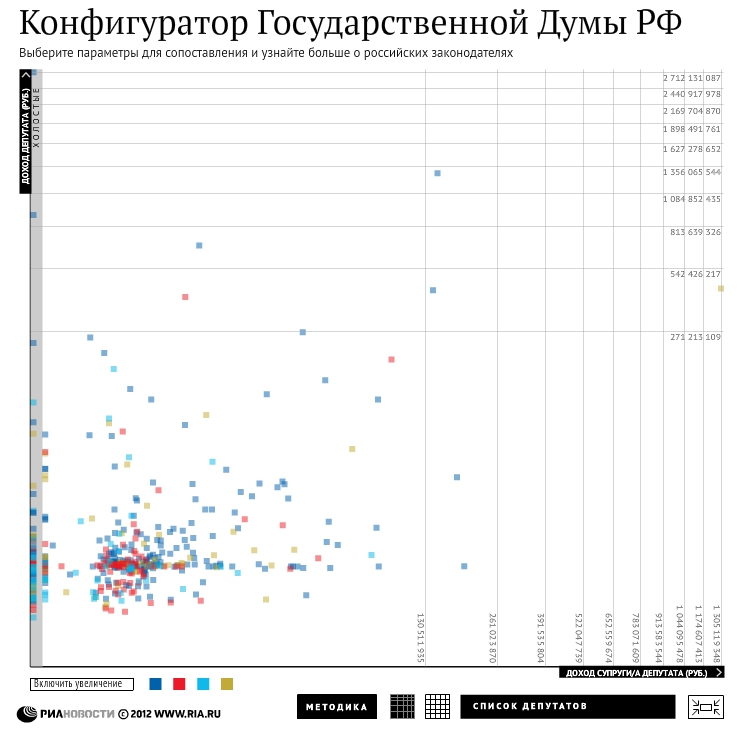
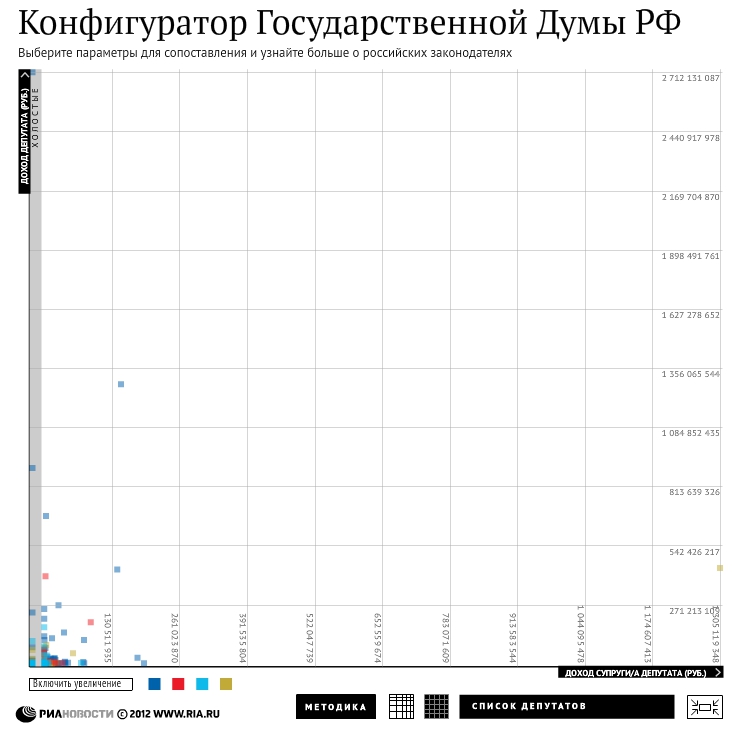
Это менее известный тип шкал. Он отличается от остальных тем, что расстояние между рисками, соответствует числам возведенным в степень. То есть получается, что расстояние между соседними рисками постоянно растёт или уменьшается. Такие шкалы удобны, когда мы хотим показать на одном графике более детально какую-то группу значений, но при это не хотим потерять из вида, значения которые, сильно отличаются от этой группы. Чем-то это похоже на логарифмическую шкалу, но здесь идёт акцент не на всем промежутке, а только на отдельной его части. Это хорошо видно на примере РИА новости, где они использовали степенные шкалы, чтобы сгладить выбросы по доходам отдельных депутатов.

Со степенной шкалой

С равномерной шкалой

То есть степенные шкалы используются когда данные смещены в ту или иную сторону.

Сравнение шкал

Чтобы удобно сравнить и понять как использовать ту или иную шкалу, я сделал небольшой инструмент. На нём можно выбрать разные наборы данных и понять, как они выглядят на разных шкалах.

Источник