Для чего нужна минимизация логических функций
Минимизация булевых функций. Минимизирующие карты Карно. Метод Куайна-МакКласки
Ясно, что при разработке логических схем, немаловажной является задача минимизации количества используемых элементов (другими словами, логических операций).
В связи с этим, возникает задача минимизации логических функций в некотором классе формул. В частности, в классах ДНФ и КНФ.
Минимальная ДНФ Такая ДНФ, которая содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей ДНФ. Минимальная КНФ Такая КНФ, которая содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей КНФ.
Процесс нахождения минимальных форм, собственно, и называется минимизацией. В простых случаях, для минимизации достаточно тождественных преобразований. В более сложных – используются специальные алгоритмы.
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя членами, содержащими одинаковые переменные, вхождения которых (с отрицанием и без) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
\[ \;\overline
Аналогично для КНФ:
\[ (\;\overline
Возможность поглощения следует из очевидных равенств
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск членов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей.
Минимизирующие карты Карно
Графический способ минимизации булевых функций. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как построенная соответствующим образом таблица истинности функции.
Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.
В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.
Булевы функции \(N\) переменных, представленные в виде СДНФ или СКНФ, могут иметь в своём составе \(2^N\) различных элементарных членов.
Например, для функции двух переменных, заданной таблицей истинности:
Минимизация логических функций
Минимизация логических функций
Преобразование логических функций с целью упрощения их аналитического представления называются минимизацией.
Понятие «упрощение» требует определенных договоренностей, что под этим будет пониматься. Упрощение можно рассматривать с точки зрения числа переменных в получаемоq эквивалентной функции, уменьшения количества отрицаний в результирующем выражении, более простой схемотехнической реализации при переводе получающейся ФАЛ на уровень интегральных микросхем и так далее.
Мы будем считать, что дизъюнктивная или конъюнктивная нормальная форма являются минимальными, если они содержат наименьшее суммарное число переменных среди всех ДНФ или КНФ, эквивалентных ей. При этом количество отрицаний над переменными учитывать не будем.
Методы минимизации можно разделить на несколько типов:
Рассмотрим их более подробно. Рассмотрение будем проводить на основе дизъюнктивных нормальных форм. Для КНФ теоретические рассуждения будут аналогичными.
В то же время, иллюстрировать соответствующие положения будем как на примерах дизъюнктивны, так и конъюнктивных форм.
Если некоторая логическая функция 



Очевидно, что ФАЛ «Константа ноль» входит во все функции, а в ФАЛ «Константу единица» входят все функции.
Функцию 
Простыми (первичными) импликантами (имплицентами для КНФ) логической функции f называют такие элементарные произведения или элементарные суммы (для имплицент), которые сами входят в данную функцию, но никакая собственная частьэтих произведений (сумм) не входит в функцию f.
Собственной частью называют произведение, полученное путем исключения из данного произведения одного или нескольких сомножителей.
Примеры этих определений показаны в Табл. 3.1.
Схемотехника. Минимизация логических функций
Зачем это нужно?
Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы (цепи), пропорциональны числу логических операций и числу вхождений переменных или их отрицаний. В принципе любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок.
К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно. К таким методам относятся, например, метод Квайна, метод карт Карно, метод испытания импликант, метод импликантных матриц, метод Квайна-Мак-Класки и др. Эти методы наиболее пригодны для обычной практики, особенно минимизация логической функции с использованием карт Карно. Метод карт Карно сохраняет наглядность при числе переменных не более шести. В тех случаях, когда число аргументов больше шести, обычно используют метод Квайна-Мак-Класки.
В процессе минимизации той или иной логической функции, обычно учитывается, в каком базисе эффективнее будет реализовать ее минимальную форму при помощи электронных схем.
Минимизация логических функций при помощи карт Карно
Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.
В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
Возможность поглощения следует из очевидных равенств
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.
Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:
В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.
Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных: 
В общем случае можно сказать, что 2K термов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.
Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.
Аналогичным образом можно работать с функциями четырёх, пяти и более переменных. Примеры таблиц для N=4 и N=5 приведены на рисунке. Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки. Для таблиц 5 и более переменных нужно учитывать также, что квадраты 4х4 виртуально находятся друг над другом в третьем измерении, поэтому соответственные клетки двух соседних квадратов 4х4 являются сосоедними, и соответствующие им термы можно склеивать.
Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.
Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):
Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных, если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Например(для Карт на 2-ве переменные):
Минимизация логических функций
При проектировании логического устройства необходимо стремиться к тому, чтобы достичь поставленной цели с минимальными затратами. Это означает, что синтезируемая схема должна содержать минимально необходимое количество логических элементов с как можно меньшим числом входов. Для выполнения этих условий логическое выражение, используемое при синтезе, должно содержать минимальное число элементарных конъюнкций или дизъюнкций и минимально возможное число переменных в этих конъюнкциях (дизъюнкциях). СДНФ и СКНФ логической функции не удовлетворяют этим требованиям. Поэтому, прежде чем приступить к разработке функциональной схемы логического устройства, нужно получить минимальную форму логической функции. ДНФ (КНФ) называется минимальной, если она содержит минимальное число букв. Чтобы получить минимальную форму логической функции, ее необходимо минимизировать.
Существует несколько методов минимизации логических функций:
-метод непосредственных преобразований;
Метод непосредственных преобразований основан на применении с целью минимизации логической функции аксиом и теорем алгебры логики. Результатом минимизации должна стать тупиковая форма логической функции, то есть такое логическое выражение, к слагаемым которого больше не могут быть применены операции склеивания. Следует иметь в виду, что для одной функции может существовать несколько тупиковых форм. Но не каждая тупиковая форма является минимальной. Минимальной формой является тупиковая форма логической функции минимальной длины. В общем случае чтобы найти минимальную форму необходимо перебрать все тупиковые формы.
Диаграмма Вейча (карта Карно) является упрощенной формой записи таблицы истинности логической функции. Основное отличие между диаграммой Вейча и картой Карно состоит в нумерации строк и столбцов таблицы. Рассмотрим методику минимизации логической функции с помощью диаграммы Вейча.
| х2 | 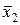 |
х2 |
| ||
| х1 | х1 | ||||
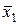 | 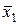 | ||||
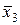 |  х3 х3 | 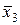 |
х2 |
| ||
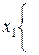 | 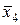 | ||
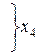 | |||
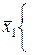 | |||
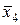 | |||
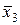 |  х3 х3 | 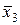 |
Рисунок 5.6 – Примеры диаграмм Вейча
Цифры, записанные в клетки диаграмм Вейча на рисунке 5.6, представляют собой номера наборов переменных в таблице истинности.
При склеивании переменных нужно руководствоваться следующими правилами:
б) в контуры можно объединять только соседние клетки, которые содержат единицы (нули). Соседними (рядом расположенными) считаются, в том числе, клетки, расположенные на противоположных сторонах диаграммы (в противоположных строках или столбцах);
в) каждой единичной клетке отвечает конъюнкция логических переменных, которые определяют данную клетку. Каждой нулевой клетке отвечает дизъюнкция инверсий логических переменных, что определяют данную клетку;
г) выражения, которые отвечают контурам, не содержат тех переменных, чьи границы пересекаются площадью, ограниченной данным контуром (другими словами, те переменные, которые в данном контуре имеют и прямое и инверсное значение – склеиваются);
д) выражение логической функции может быть записано по соответствующей ей диаграмме Вейча в дизъюнктивной или конъюнктивной форме. Дизъюнктивная форма составляется в виде дизъюнкции конъюнкций, которые отвечают единичным контурам, выделенным на диаграмме для определения функции; конъюнктивная – в виде конъюнкции дизъюнкций, которые отвечают нулевым контурам;
е) для контуров, которые охватывают разное количество клеток, получаются выражения разной сложности. Поэтому для данной логической функции можно записать по ее диаграмме Вейча несколько алгебраических выражений, которые отличаются по сложности. Наиболее сложное выражение получают в том случае, когда каждой клетке отвечает свой отдельный контур. Это выражение представляет собой СДНФ или СКНФ данной функции.
Для получения по диаграмме Вейча минимального выражения логической функции следует руководствоваться правилом: единицы и нули должны объединяться минимальным числом наибольших контуров.
Рассмотрим пример минимизации логической функции трех переменных у = f(x1, x2, x3), заданной таблицей истинности (рисунок 5.5), воспользовавшись методом Карно-Вейча. Для начала воспользуемся представлением функции в дизъюнктивной нормальной форме. В этом случае диаграмма Вейча должна быть заполнена, как показано на рисунке 5.7.
Рисунок 5.7 – Минимизация функции к виду ДНФ
Из рисунка 5.7 видно, как можно наилучшим образом объединить единицы в единичные контуры. При этом в контуры могут входить и ячейки с номерами запрещенных наборов (то есть элементами которых являются «*»). В результате такого объединения получим тупиковую форму логической функции в виде дизъюнкции конъюнкций (число которых равно числу единичных контуров) входных переменных, которые не склеились:
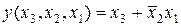
Если для представления логической функции после минимизации выбрана конъюнктивная нормальная форма, то в диаграмме Вейча объединяют нули в нулевые контуры. Как и в предыдущем случае, в нулевые контуры могут быть включены ячейки, элементами которых являются «*» (рисунок 5.8).
Рисунок 5.8 – Минимизация функции к виду КНФ
Тупиковая форма логической функции после минимизации представляет собой конъюнкцию дизъюнкций (число дизъюнкций равно числу нулевых контуров) инверсных значений тех входных переменных, которые не склеились:
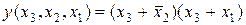
Выражения (5.3) и (5.4) описывают структуру логического устройства, алгоритм функционирования которого задан функцией у (рисунок 5.5). Несмотря на то, что полученные выражения разные по виду, а, следовательно, и схема логического устройства в каждом случае будет выполнена по разному, сигналы на выходах этих схем на одних и тех же номерах разрешенных наборов входных переменных будут одинаковы.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Методы минимизации логических функций
Выбранный для просмотра документ Мулдашева.doc
Работа по теме
МЕТОДЫ МИНИМИЗАЦИИ
ЛОГИЧЕСКИХ ФУНКЦИЙ
Ключевые понятия: логические выражения, логические функции, методы минимизации, инверсия, конъюнкция, дизъюнкция, импликация, эквиваленция.
Содержание
Введение
Люди, далекие от техники, часто смотрят на ЭВМ и другие цифровые электронные устройства как на нечто таинственное и непостижимое. Тем не менее, все эти устройства работают в строгом соответствии с четкими логическими законами. Знание и понимание этих законов помогает в общении с компьютером и другими цифровыми устройствами.
Принципы построения схемы цифрового устройства задается логическими функциями. Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы (цепи), пропорциональны числу логических операций и числу вхождений переменных или их отрицаний. В принципе любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок [13].
К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно.
Упрощенная функция будет содержать меньше операций и комбинаций аргументов, а значит и схема, реализующая функцию, будет содержать меньше элементов, т.е. будет дешевле и надежнее [18].
В связи с этим минимизация логических функций особенно актуальна.
Целью работы является изучение методов минимизации функций алгебры логики.
Объектом работы стал процесс минимизации логических функций.
Предмет исследования – методы минимизации логических функций и методика преподавания этой темы в профильных классах.
изучить основные элементы математической логики;
исследовать методы минимизации логических функций;
подобрать задачи для самостоятельной работы;
решить описанными методами подобранные задачи.
Работа состоит из введения, двух разделов, заключения и списка использованной литературы.
Во введении обосновывается актуальность темы, определяется цель и задачи исследования.
В первом разделе рассматриваются логические основы функционирования ЭВМ.
Во втором разделе раскрываются методы минимизации логических функций, приводятся примеры решения задач описанными методами.
В заключении подводятся общие итоги исследования.
Логические основы функционирования ЭВМ
Элементы математической логики
Компьютеры – это автоматические устройства, принципы работы которых базируются на элементарных законах двоичной логики.
Вычислительные машины всех поколений состояли и состоят из логических элементов и элементов памяти, принимающих два значения (бита) 0 и 1. Вся обработка информации в ЭВМ всех ее логических блоков, логических схем и устройств опиралась и будет опираться на законы и принципы математической логики [8].
Логика (от древнегреческого logos, означающего «слово, мысль, понятие, рассуждение, закон») – это древнейшая наука, изучающая правильность суждений, рассуждений и доказательств.
Математическая логика – это математическая дисциплина, изучающая технику доказательств [8].
Основоположником математической логики является великий немецкий математик Готфрид Вильгельм Лейбниц (1646 – 1716 гг.). Он выдвинул идею о применении в логике математической символики и построении логических исчислений, поставил задачу логического обоснования математики, сыграл важную роль в истории создания электронно-вычислительных машин: предложил использовать для целей вычислительной математики бинарную систему счисления. На заложенном Лейбницем фундаменте ирландский математик Джордж Буль построил здание новой науки – математической логики, – которая в отличие от обычной алгебры оперирует не числами, а высказываниями. В честь Д.Буля логические переменные в языке программирования «Паскаль» впоследствии назвали булевскими.
Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем, которые лежат в основе работы любого компьютера. Суждения в математической логике называют высказываниями или логическими выражениями.
Высказывание – это любое утверждение, относительно которого можно сказать истинно оно или ложно, т.е. соответствует оно действительности или нет; это символическая запись, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками) [2].
Различные логические выражения (высказывания) могут принимать только два значения: «истинно» или «ложно». Каждая логическая переменная может принимать только одно значение. Существуют разные варианты обозначения истинности и ложности:
Высказывания могут быть простыми и сложными. Простые соответствуют алгебраическим переменным, а сложные являются аналогом алгебраических функций. Функции могут получаться путем объединения переменных с помощью логических действий (операций) [3].
Рассмотрим логические операции, с помощью которых можно записать любое логическое выражение.
Самой простой логической операцией является операция НЕ (по-другому ее часто называют отрицанием, дополнением или инверсией и обозначают 
Таким образом, отрицанием 



Логическая операция НЕ является унарной, т.е. имеет всего один операнд. Определение отрицания может быть записано с помощью так называемой таблицы истинности, в которой указано, указано, какие значения истинности (1, 0) принимает отрицание 

Операции И, ИЛИ, НЕ образуют полную систему логических операций, из которой можно построить сколь угодно сложное логическое выражение. Но помимо них существуют и другие логические операции.
Логическое следование (импликация) – это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием ( 





Запишем это определение в виде таблицы истинности:
Логические функции и их преобразование
Логическая функция – это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1 [1].
Каждая логическая функция может быть задана большим количеством различных по виду функций. Но даже любую достаточно сложную логическую функцию можно реализовать, имея относительно простой набор базовых логических операций. Наиболее известный базис – это набор функций «и», «или», «не».
Для операций конъюнкции, дизъюнкции и инверсии определены законы, позволяющие производить тождественные (равносильные) преобразования логических выражений [1, 11]:
закон двойного отрицания: 
коммутативность конъюнкции : 
коммутативность дизъюнкции: 
ассоциативность конъюнкции: 
ассоциативность дизъюнкции: 
дистрибутивность конъюнкции относительно дизъюнкции :
дистрибутивность дизъюнкции относительно конъюнкции: 
закон исключенного третьего: 
закон непротиворечия: 
замена импликации: 
правила Порецкого: 

правила свертки: 

Основываясь на законах, можно выполнять упрощение сложных логических выражений.
Исходными, из соображений удобства последующих преобразований, приняты следующие две канонические формы 1 представления функций: совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ).
Прежде чем перейти к СДНФ и СКНФ введем некоторые понятия.
Элементарной конъюнкцией называется конъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причём среди переменных могут быть одинаковые [15].
Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причём среди переменных могут быть одинаковые [15].
Всякую дизъюнкцию элементарных конъюнкций называют дизъюнктивной нормальной формой, то есть ДНФ [15].
Например, выражение 
Всякую конъюнкцию элементарных дизъюнкций называют конъюнктивной нормальной формой, то есть КНФ [15].
Например, выражение 
Совершенной ДНФ (СДНФ) называется ДНФ, в которой нет равных элементарных конъюнкций, и все они содержат одни и те же переменные, причём каждую переменную только один раз (возможно с отрицанием) [15].
Например, выражение 

Совершенной КНФ (СКНФ) называется КНФ, в которой нет равных элементарных дизъюнкций, и все они содержат одни и те же переменные, причём каждую переменную только один раз (возможно с отрицанием) [15].
Приведу алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы [3]:
переход от произвольного задания функции к ДНФ
Этот переход сводится к опусканию общих для нескольких переменных инверсий, раскрытию скобок и объединению, если они возникают, одинаковых членов с использованием законов:
закон исключенного третьего: 
закон непротиворечия: 
переход от ДНФ к КНФ
Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения. Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
В
переход от КНФ к ДНФ
Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения):
переход от КНФ к СКНФ
переход от ДНФ к СДНФ
п
Для получения СДНФ и СКНФ из таблиц истинности необходимо выполнить следующие 4 пункта алгоритма [15]:
Конструирование СДНФ и СКНФ начинается с таблицы истинности.
Отметим те строки таблицы, выходы которых равны
Выписываем для каждой отмеченной строки комбинацию переменных через знак
Знаки операции отрицания расставляем следующим образом:
если переменная равна 1, то запишем саму эту переменную, если же она равна 0, то запишем ее отрицание.
если переменная равна 0, то запишем саму эту переменную, если же она равна 1, то запишем ее отрицание.
Все полученные выражения связываем операцией
Получив СДНФ или СКНФ, можно составить электронную схему, реализующую данную логическую функцию. Для ее постороения требуется 3 логических элемента [9, 18]:
Но чаще всего СДНФ содержит много слагаемых и задача заключается в том, чтобы уменьшить их число и упростить логическое выражение. Для упрощения логических функций можно использовать законы логики, приведенные выше. С этой же целью были разработаны и специальные методы, речь о которых пойдет в следующем разделе.
Минимизация логических функций
Как отмечалось в предыдущей главе, логическая функция может быть представлена в виде таблицы истинности или в виде СДНФ (совершенной дизъюнктивной нормальной формы) или СКНФ (совершенной конъюнктивной нормальной формы) и может быть использована для получения логической схемы устройства. Однако полученная логическая схема, как правило, не будет оптимальна. Поэтому важным этапом синтеза логических схем является минимизация логических функций.
Минимизацией называется преобразование логических функций с целью упрощения их аналитического представления.
Существуют два направления минимизации:
Кратчайшая форма записи (при этом получаются кратчайшие формы КДНФ, ККНФ, КПНФ);
Получение минимальной формы записи (получение минимального числа символов для записи всей функции сразу).
Но следует учесть, что ни один из способов минимизации не универсален.
Для минимизации функций алгебры логики был разработан ряд методов:
метод непосредственных преобразований логических функций;
метод минимизации логических функций при помощи карт Карно;
метод Петрика и другие.
Остановимся более подробно на первых двух методах.
Метод непосредственных преобразований логических функций
Одним из простых методов минимизации является метод непосредственных преобразований, который осуществляется с использованием основных теорем алгебры логики [11].
При применении данного метода:
Записываются СДНФ логических функций,
Форма преобразуется и упрощается с использованием аксиом алгебры логики, при этом, в частности, выявляются в исходном СДНФ соседние термы (члены), в которых есть по одной не совпадающей переменной.
По отношению к соседним термам применяется закон склейки.
Термы, образованные при склеивании называются импликантами.
Полученные после склейки импликанты по возможности склеивают до тех пор, пока склеивание становится невозможным.
П
Пусть дана функция
Минимизируем ее описанным выше методом. Для этого добавим еще одно слагаемое 
П
Рассмотренный метод минимизации путем непосредственных преобразований достаточно прост, особенно при небольшом числе переменных. Недостатком метода является то, что он не указывает строго формализованный путь минимизации. При большом числе переменных минтермы могут группироваться по-разному, в результате чего можно получить различные упрощенные формы заданной функции. При этом нельзя быть уверенным в том, что какая-то из этих форм является минимальной. Возможно, что получена одна из тупиковых форм, которая больше не упрощается, не являясь при этом минимальной.
Метод минимизации логических функций при помощи карт Карно
Карта Карно или карта (диаграмма) Вейча – графический способ минимизации функций алгебры логики.
Карты Карно удобны при небольшом числе переменных.
Карты Карно представляют собой определенную таблицу истинности обычно для двух, трех и четырех переменных и отличаются друг от друга способом обозначения строк и столбцов таблиц истинности.
Н
Расположение групп переменных x не имеет значения, необходимо лишь, чтобы каждая клетка отличалась от любой соседней лишь на одну переменную. Согласно принятой форме построения карт соседними также считаются клетки первой и последней строк, клетки первого и последнего столбцов. Число клеток карты равно числу возможных комбинаций значений переменных (термов) и в каждую клетку записывается значение логической функции, соответствующее данному набору переменных. Если какая-то из возможных комбинаций присутствует в совершенной дизъюнктивной нормальной форме (СДНФ) записи функции, то в соответствующей клетке карты Карно ставится «1». Если какого-то терма в полученной функции нет, то в соответствующей клетке карты Карно ставится «0» [12].
Н
з
Полученные упрощенные выражения объединяют с помощью операции ИЛИ.
Т
Таким образом, соседние клетки карты Карно можно группировать для исключения переменной. Число группируемых клеток может быть и больше двух, но их число должно быть четным и они должны соприкасаться (являться соседними) друг с другом.
Допускается также иметь несколько групп перекрывающихся клеток, как в только что рассмотренном примере.
Группироваться могут также клетки первой и последней строк, первого и последнего столбцов, т. е. карту допускается сворачивать в цилиндр как по вертикальной, так и по горизонтальной оси.
Таким образом, для того чтобы получить минимизированную логическую функцию, необходимо сгруппировать все соседние клетки карты Карно, содержащие 1, а затем объединить полученные группы с помощью операции ИЛИ. Клетки, содержащие 1, которые не удалось объединить с другими клетками, образуют в минимизированной логической функции самостоятельные члены, каждый из которых содержит все переменные [12].
Рассмотрим несколько примеров карт Вейча и способы построения контуров группировки соседних клеток для получения упрощенной логической функции.
Т
приведена на рисунке 3.
На этом рисунке показан правильный способ объединения соседних ячеек, т. е. карта Вейча как бы свернута в вертикально расположенный цилиндр.
У
Таким образом, группируя соседние клетки в единый квадрат, удалось исключить две переменные ( х 1 и х 2 ) и получить простое выражение для логической функции.
Р
Карта Карно для этой функции представлена на рисунке 4:
Группируемые ячейки обведены двумя контурами. Нижний контур дает возможность исключить одну переменную х 3 и после этого в нем остается член 
В верхнем контуре можно исключить две переменные ( х 2 и х 4 ) и после этого в нем остается член 
Рассмотрим минимизацию логической функции, карта Вейча которой представлена на рис. 5.
Булево выражение этой функции имеет вид
Четыре угловые клетки можно объединить в одну группу. Это объединение позволяет исключить две переменные ( х 1 и х 2 ) и получить член 
Две единицы из первой строки можно объединить с двумя единицами из нижней строки, получить группу из четырех ячеек, которая позволяет исключить две переменные ( х 1 и х 3 ) и получить член 
Наконец, единственную оставшуюся единицу (из второй строки и последнего столбца) можно объединить с клеткой, находящейся над ней, и это позволит исключить одну переменную ( х 4 ) и получить член 
Таким образом, мы получим минимизированную логическую функцию
Метод карт Карно (диаграмм Вейча), по существу, упрощает нахождение склеиваемых конъюнкций в СДНФ исходной логической функции.
Минимизация функций алгебры логики описанными методами
В данной главе представлены подобранные нами функции и примеры их минимизации с помощью рассмотренных выше методов.
Упростить, используя карты Карно для функции 2 переменных:
К
Во втором столбце можно исключить переменную х 1 и получить упрощенное выражение 
Полученные упрощенные выражения соединим операцией ИЛИ.
Т
Д
Во второй строке можно исключить переменную 

Полученные упрощенные выражения соединим операцией ИЛИ.
Т
Упростить, используя карты Карно для функции 3 переменных:
Диаграмма Вейча для этой функции будет иметь вид:
В 

Во второй строке можно исключить переменную х 3 и получить упрощенное выражение 
В последнем столбце можно исключить переменную х 1 и получить упрощенное выражение 
Полученные упрощенные выражения соединим операцией ИЛИ.
Т
Д
В первой строке можно исключить переменную х 3 и получить упрощенное выражение 

Полученные упрощенные выражения соединим операцией ИЛИ.
Т
Нами был найден и второй способ минимизации данной функции.
Тогда диаграмма Вейча для этой функции будет иметь вид:
В первой строке можно исключить переменную х 3 и получить упрощенное выражение 
В 

Полученные выражения соединим операцией ИЛИ.
Т
О
Д



о втором столбце можно исключить переменную х 1 и получить упрощенное выражение 
Полученные упрощенные выражения соединим операцией ИЛИ.
Т
Диаграмма Вейча для этой функции будет иметь вид:
В 

Во второй строке можно исключить переменную х 3 и получить упрощенное выражение 
Полученные упрощенные выражения соединим операцией ИЛИ.
Т
Диаграмма Вейча для этой функции будет иметь вид:
В 

Во второй строке можно исключить переменную х 2 и получить упрощенное выражение 
Полученные упрощенные выражения соединим операцией ИЛИ.
Т
О
Упростить, используя карты Карно для функции 4 переменных:
Д
Группируем угловые клетки, в которых можно исключить переменные х 1 и х 2 и получить упрощенное выражение 
В первом столбце можно исключить переменную х 1 и получить упрощенное выражение 
Полученные упрощенные выражения соединим операцией ИЛИ.
Т
О

Диаграмма Вейча для этой функции будет иметь вид:
Во второй и третьей строке группируем четыре центральные соседние клетки, в которых можно исключить переменные х 1 и х 2 и получить упрощенное выражение 
В 

Полученные упрощенные выражения соединим операцией ИЛИ.
Т
О

Диаграмма Вейча для этой функции будет иметь вид:
В 

В последней строке группируем четыре соседние клетки, в которых можно исключить переменные х 2 и х 3 и получить упрощенное выражение 
Полученные упрощенные выражения соединим операцией ИЛИ.
Т
О

Д
В последнем столбце группируем угловые клетки, в которых можно исключить переменную х 1 и получить упрощенное выражение 
В двух последних строках группируем четыре соседние клетки, в которых можно исключить переменные х 2 и х 4 и получить упрощенное выражение 
Полученные упрощенные выражения соединим операцией ИЛИ.
Т
В данной главе были представлены функции двух, трех и четырех переменных, которые минимизировались с помощью диаграмм Вейча. Мною были наглядно продемонстированы и описаны особенности применения данного метода минимизации на различных функциях, в том числе и в совокупности с методом непосредственного преобразования функций алгебры логики.
Заключение
Представленная работа посвящена методам минимизации функций алгебры логики. В процессе работы были:
изучены основные элементы математической логики;
исследованы методы минимизации логических функций;
подобраны задачи для самостоятельной работы;
решены описанными методами подобранные задачи.
Мною было подробно рассмотрено 2 метода минимизации логических функций:
метод непосредственных преобразований логических функций, осуществляемый с использованием теорем алгебры логики;
метод минимизации с помощью диаграмм Вейча (карт Карно).
Первый метод получил широкое распространение даже в школьных учебниках информатики (например, учебники 10-11 класса Н. Угриновича [20, 21], Л. Щауцуковой [22]), поскольку является одним из простых методов упрощения функций алгебры логики. Задания, представленные в учебниках указанных авторов, достаточно разнообразны:
упростить логическую формулу с помощью законов алгебры логики;
по заданной функции построить логическую схему;
упростить переключательную схему;
доказать с помощью таблицы истинности логическое выражение;
построить для данной функции таблицу истинности.
Второй метод позволяет быстро и легко исключить отличающиеся переменные и получить упрощенное выражение, которое не всегда может быть минимальным. Поэтому данный метод следует рассматривать в совокупности с методом непосредственных преобразований логических функций.
Данная тема имеет практическое значение в микроэлектронике. Кроме того, ЕГЭ по информатике и ИКТ содержит некоторое количество заданий, связанных с алгеброй логики, которые мы разделили на 4 группы [4].
Первая группа – это задания, требующие указать логическое выражение, равносильное данному.
Вторая группа – задания на нахождение фрагментов таблиц истинности, соответствующих данному выражению.
И четвертая группа – это задания на определение структурной формулы, соответствующей данной логической схеме.
Заданий конкретно касающихся минимизации логических функций мне не встретилось, но имеющиеся в тестах задания требуют достаточно глубоких знаний в области алгебры логики.
В связи с усложнением вступительных испытаний в высшие учебные заведения можно предположить, что в скором времени в тестах, а значит и в образовательных программах, могут появиться задания на упрощение и минимизацию логических функций.
Список литературы
Гаврюкова Г. А. Логика в информатике [Электронный ресурс]. – Режим доступа: http://gmoi.narod.ru/s/u/logic.htm (21 окт. 2010).
Ивин А. А. Логика : Учебное пособие. – 2-е изд. – М.: Знание, 1998. – 233 с.
Игошин В. И. Математическая логика и теория алгоритмов: Учебное пособие для студ. высш. учеб. заведений. – 2-е изд., стер. – М.: Академия, 2008. – 448 с.
Информатика и ИКТ. Подготовка к ЕГЭ-2009. Вступительные испытания. / Под ред. Ф. Ф. Лысенко. – Ростов н/Д: Легион-М, 2009. – 208 с.
Информатика : Учебник / Б. В. Соболь [и др.]. – 3-е изд., доп. и перераб. – Ростов н/Д: Феникс, 2007. – 446 с.
Информатика : Учебное пособие / А. В. Могилев, Н. И. Пак, Е. К. Хеннер. – 3-е изд. – М.: Академия, 2004. – 848 с.
Калабеков Б. А. Цифровые устройства и микропроцессорные системы: Учебник для техникумов связи. – М.: Горячая линия – Телеком, 2000. – 336 с.
Каймин В. А. Информатика : Учебник. – 2-е изд., перераб. и доп. – М.: ИНФРА-М, 2001. – 272 с.
Коваленко А. А, Петропавловский М. Д. Основы микроэлектроники: Учебное пособие. – М.: Академия, 2006. – 240 с.
Львовский М. Б. Методическое пособие по информатике для учащихся 9-11 классов, изучающих IBM PC [Электронный ресурс]. – Режим доступа: http://markbook.chat.ru/book/oglavlen.htm (19 сент. 2010).
Математические основы информатики. Элективный курс : Учебное пособие / Е. В. Андреева, Л. Л. Босова, И. Н. Фалина. – М.: БИНОМ. Лаборатория знаний, 2005. – 328 с.
Минимизация логических функций [Электронный ресурс]. – Режим доступа: http://www.reltehnika.ru/book/2_1.html (19 авг. 2010).
Основы микроэлектроники : Учебное пособие для вузов / Н. А. Аваев, Ю. Е. Наумов, В. Т. Фролкин. – М.: Радио и связь, 1991. – 288 с.: ил.
Практикум по информатике и информационным технологиям / Н. Д. Угринович, Л. Л. Босова, Н. И. Михайлова. – 2-е изд., испр. – М.: БИНОМ. Лаборатория знаний, 2004. – 394 с.
Прикладная математика : Пособие / И. Н. Ревчук, В. К. Пчельник. – Гродно: ГрГУ им. Я. Купалы, 2007. – 128 с.
Рабкин Е. Л., Фарфоровская Ю. Б. Дискретная математика: булевы функции и элементы теории графов: Методические указания и контрольные задания [Электронный ресурс]. – Режим доступа: http://dvo.sut.ru/libr/himath/w163rabk/index.htm (2 7 авг. 2010).
Савельев А. Я. Основы информатики : Учебник для вузов. – М.: МГТУ им. Н. Э. Баумана, 2001. – 328 с., ил.
Степаненко И. П. Основы микроэлектроники : Учебное пособие для вузов. – 2-е изд., перераб. и доп. – М.: Лаборатория Базовых Знаний, 2001. – 488 с.
Теория и методика обучения информатике : Учебник / [М. П. Лапчик, И. Г. Семакин, Е. К. Хеннер, М. И. Рагулина и др.]; под ред. М. П. Лапчика. – М.: Академия, 2008. – 592 с.
Угринович Н. В. Информатика и ИКТ. 10 класс. Профильный уровень. – 3-е изд., испр. – М.: Бином. Лаборатория знаний, 2008. – 387 с.
Угринович Н. В. Информатика и информационные технологии : Учебник для 10-11 классов. – М.: БИНОМ. Лаборатория знаний, 2003. – 512 с.
Шауцукова Л. З. Информатика 10 – 11. – М.: Просвещение, 2004. – 420 с.
1 Канонические формы – запись формы функции по единым правилам.
Выбранный для просмотра документ автор.doc
Мулдашева Светлана Викторовна
Свято-Покровская православная классическая гимназия г. Саратова
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
Курс повышения квалификации
Современные педтехнологии в деятельности учителя
Ищем педагогов в команду «Инфоурок»
Содержание
Введение
Люди, далекие от техники, часто смотрят на ЭВМ и другие цифровые электронные устройства как на нечто таинственное и непостижимое. Тем не менее, все эти устройства работают в строгом соответствии с четкими логическими законами. Знание и понимание этих законов помогает в общении с компьютером и другими цифровыми устройствами.
Принципы построения схемы цифрового устройства задается логическими функциями. Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы (цепи), пропорциональны числу логических операций и числу вхождений переменных или их отрицаний. В принципе любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок.
К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно.
Упрощенная функция будет содержать меньше операций и комбинаций аргументов, а значит и схема, реализующая функцию, будет содержать меньше элементов, т.е. будет дешевле и надежнее.
В связи с этим минимизация логических функций особенно актуальна.
Целью работы является изучение методов минимизации функций алгебры логики.
Объектом работы стал процесс минимизации логических функций.
Предмет исследования – методы минимизации логических функций и методика преподавания этой темы в профильных классах.
Задачи исследования:
Работа состоит из введения, двух разделов, заключения и списка использованной литературы.
Во введении обосновывается актуальность темы, определяется цель и задачи исследования.
В первом разделе рассматриваются логические основы функционирования ЭВМ.
Во втором разделе раскрываются методы минимизации логических функций, приводятся примеры решения задач описанными методами.
В заключении подводятся общие итоги исследования.

































