Для чего нужна переходная кривая

Переходная кривая

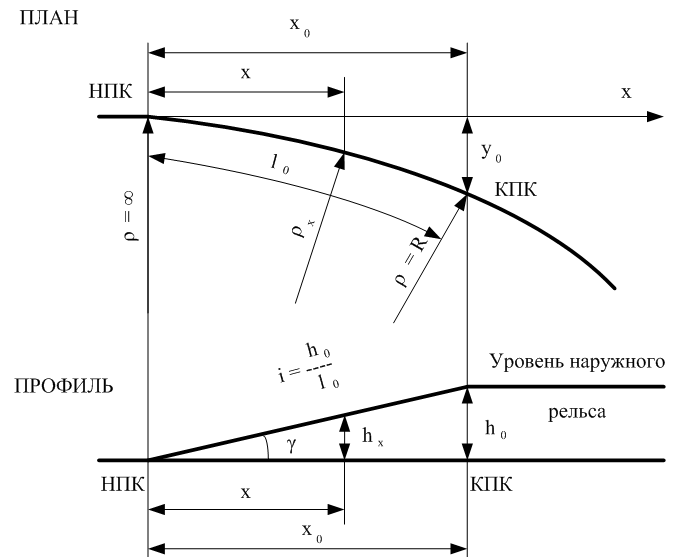
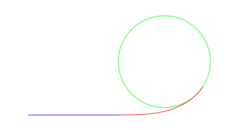
Переходная кривая — кривая переменной кривизны, сопрягающая круговую кривую с прямым участком железнодорожного пути. Переходная кривая обеспечивает постепенное изменение центробежной силы при входе поезда в криволинейный участок пути. В пределах переходной кривой линейно возрастает необходимое в круговой кривой возвышение наружного рельса. Переменный радиус переходной кривой ρ плавно изменяется от ρ = ∞ в точках HK и KK сопряжения с прямой до ρ = R в точках КПК₁ и КПК₂ сопряжения переходной кривой с кривой радиуса R. Разбивка переходной кривой производится по радиоидальной спирали, кривизна которой изменяется пропорционально её длине.

Элементы переходной кривой (m, Т_ρ и другие) для облегчения их полевой разбивки приводятся в специальных таблицах. В практических расчётах приближённо считают, что переходная кривая очерчена по кубической параболе.

Длина переходной кривой при проектировании железной дороги принимается в соответствии со Строительными нормами и правилами в зависимости от радиуса круговой кривой и скоростей движения поездов. При проектировании реконструкции существующих железных дорог и строительства вторых путей часто возникает необходимость удлинения переходной кривой.

Источник

Назначение переходных кривых. Общая теория перех. кр.

Переходные кривые обеспечивают плавность входа подвижного состава в кривые за счет плавного нарастания кривизны.
При изменении радиуса от ¥ в НПК до радиуса круговой криво R в КПК.В переделах переходной кривой также плавно увеличивается возвышение наружного рельса от 0 до h.

Центробежная сила, возникающая в любой точке переходной кривой, должна уравновешиваться центростремительной, возникающей за счет наличия возвышения наружного рельса

Это требование будет выполнено, если кривизна будет нарастать пропорционально увеличению длины переходной кривой.
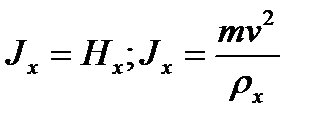
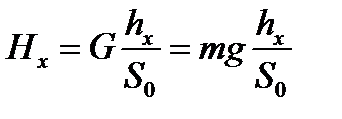
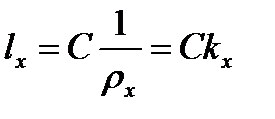
где С=Rl₀ – параметр кривой.

Этому уравнению удовлетворяет кривая, называемая радиоидальной спиралью. В прямоугольной системе координат она имеет вид:

Во многих случаях представляется возможным ограничиться первыми членами рядов и использовать уравлениня кубической параболы:

Кубическая парабола отличается от радиоидальной спирали тем, что ее кривизна меняется пропорционально не протяжению переходной кривой, а ее проекции на ось Х.Кубическая парабола может быть применена для разбивки переходной кривой, если выполняется требование:
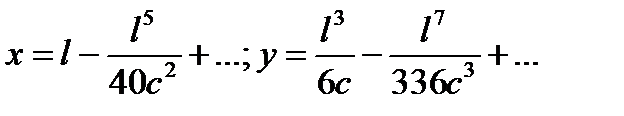
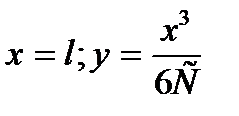
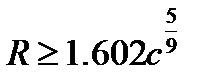
Длина переходной кривой l₀ определяется из условия обеспечения плавного отвода возвышения наружного рельса, принятого в круговой кривой, и безопасного подъема колеса, идущего по возвышению наружного рельса.

При прямолинейном отводе возвышение наружного рельса длина переходной кривой определяется по зависимости
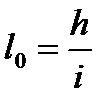
где i – уклон отвода возвышения наружного рельса.

Длина переходной кривой принимается кратной 10 м и не должна быть короче 20 м.

По второму условию ограничивается скорость нарастания непогашенного горизонтального ускорения a_н за время прохождения переходной кривой

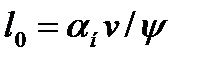
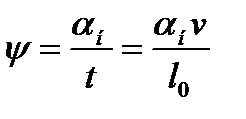
Если принять l₀=h/i и v®км/ч, h®мм, получим

Обычно это требование выполняется.

Разбивка переходных кривых.

Наиболее распространенным является способ сдвижки круговой кривой во внутрь к центру. От имеющегося на местности тангенсного столика Т₀ откладывают расстояние m₀ и получают начало переходной кривой НПК.Переходную кривую строят по ординатам в соответствии с ее уравнением, задаваясь значениями х=10; 20 и до х₀.Для этого принимается такая последовательность расчета.
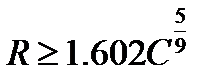
1. Определяют длину переходной кривой и параметр С=Rl_0. 2. Принимают вид переходной кривой (кубическую параболу или радиоидальную спираль). Кубическую параболу применяют при условии

3. Определяют угол поворота на протяжении переходной кривой

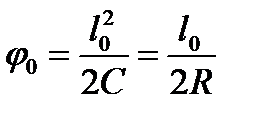
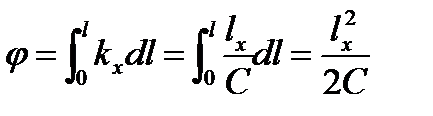
Для конца переходной кривой

4. Определяют возможность разбивки переходных кривых по условию 2j₀

7. Расстояние от начала переходной кривой до первоначального положения предельного столбика
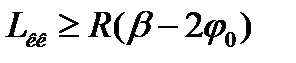
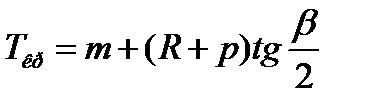
8. Полная длина новой кривой (с переходными кривыми):
L_кр=2l₀+R(b-2j₀).
Суммированный тангенс новой кривой:

Во многих случаях значения m₀ и р находят приближенным методом, имея ввиду, что:

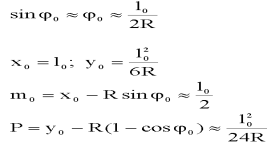
На эксплуатируемых линиях указанный способ применяется, когда сдвижка Р не превышает 25 см.

Дата добавления: 2018-05-12 ; просмотров: 2184 ; Мы поможем в написании вашей работы!

Источник

Круговые и переходные кривые.

Главными точками кривой, определяющими её положение на местности, являются вершина угла ВУ, начало кривой НК, середина кривой СК и конец кривой КК (рис. 15.3).

Рис. 15.3 Схема круговой кривой

Основные элементы кривой – её радиус R и угол поворота a. К основным элементам относятся также:

Во время изысканий угол a измеряют, а радиус R назначают. Остальные элементы вычисляют по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НК, О (центр окружности):

Домер вычисляют по формуле

. (15.2)

Вместо вычислений по формулам можно воспользоваться таблицами для разбивки кривых на железных дорогах, где по заданным радиусу и углу поворота сразу находят значения Т, К, Б и Д.

В месте поворота трассы пикетаж ведётся по кривой. Пикетажное положение главных точек кривой определяют по формулам:

Правильность вычислений контролируют по формулам:

Измерено a = 18°19¢ и задан радиус R = 600 м. Вершина угла расположена на пикете 6 + 36,00.

По формулам (15.1) и (15.2) или по таблицам находим элементы кривой: Т = 96,73 м; К = 191,81 м; Д = 1,65 м; Б = 7,75 м.

Вычислим пикетажное положение главных точек:

ПК ВУ 6 + 36,00 ПК ВУ 6 + 36,00

ПК НК 5 + 39,27 7 + 32,73

ПК КК 7 + 31,08 ПК КК 7 + 31,08

ПК НК 5 + 39,27 ПК ВУ 6 + 36,00

ПК СК 6 + 35,17 ПК СК 6 + 35,18

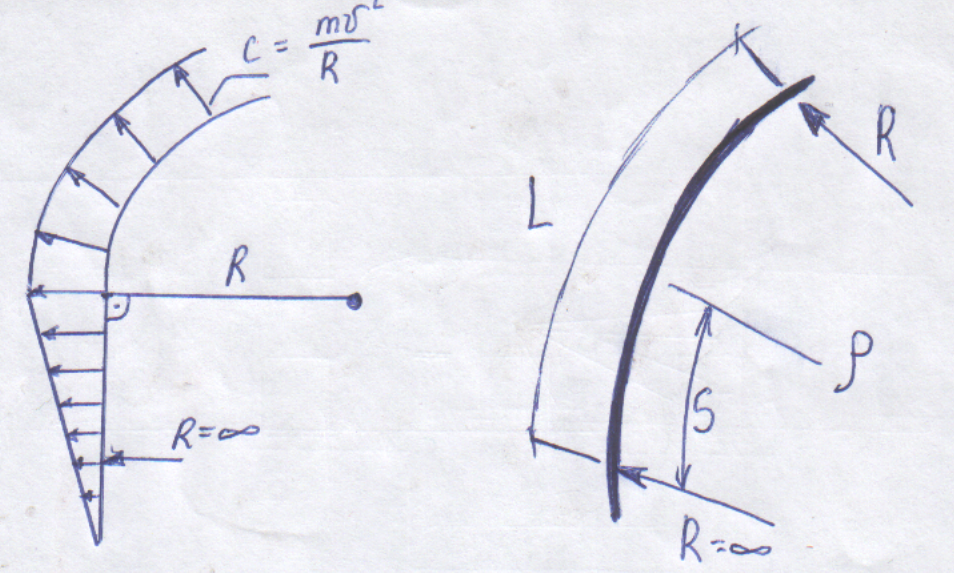
Переходные кривые. Непосредственное сопряжение прямого участка пути с круговой кривой приводит к тому, что во время движения поезда в месте сопряжения внезапно возникает центробежная сила F, прямо пропорциональная квадрату скорости движения v и обратно пропорциональная радиусу кривой . Чтобы обеспечить постепенное нарастание центробежной силы, между прямой и круговой кривой вставляют переходную кривую, радиус кривизны r которой плавно изменяется от ¥ до R. Если положить, чтобы центробежная сила менялась пропорционально расстоянию s от начала кривой, то получим

,

R – радиус кривизны в конце переходной кривой.

Индексом k отмечены значения переменных в конце переходной кривой.

Для радиуса кривизны переходной кривой в текущей точке i найдём:

где через l обозначена длина переходной кривой s_k. Кривая, описываемая уравнением (15.5), в математике называется клотоидой, или радиоидальной спиралью.

Угол поворота трассы на переходной кривой. На бесконечно малом отрезке кривой ds (рис. 15.4, а) происходит поворот трассы на угол

.

Подставляя выражение радиуса кривизны r из (15.5), получим

.

Выполним интегрирование от начала кривой НК, где j = 0 и s = 0, до текущей точки i:

,

Рис. 15.4 Схема переходной кривой:

а – углы поворота трассы: φ – в текущей точке i, β – в конце

Из полученного уравнения вытекают формулы:

; ; l = 2Rb, (15.6)

Координаты точки переходной кривой. Совместим начало координат с началом переходной кривой и направим ось x по касательной к ней (см. рис. 15.4, а). Бесконечно малому приращению дуги кривой соответствуют бесконечно малые приращения координат (рис. 15.4, б):

Разложим синус и косинус в ряд и, удержав в разложениях по два члена, подставим в них выражения для j из (15.6):

Подставляя полученные выражения в (15.7) и выполняя интегрирование, найдём:

; (15.8)

. (15.9)

Смещение начала кривой (сдвижка). На рис. 15.5 дуга НК-КПК представляет собой переходную кривую, переходящую после точки КПК в круговую. Продолжим круговую кривую до точки Q, где её направление, параллельно оси x. Обозначим через m смещение, параллельное оси x, начала переходной кривой относительно точки Q, в которой начиналась бы круговая кривая при отсутствии переходной. Через p обозначим смещение в перпендикулярном направлении. Из рис. 15.5 видно:

,

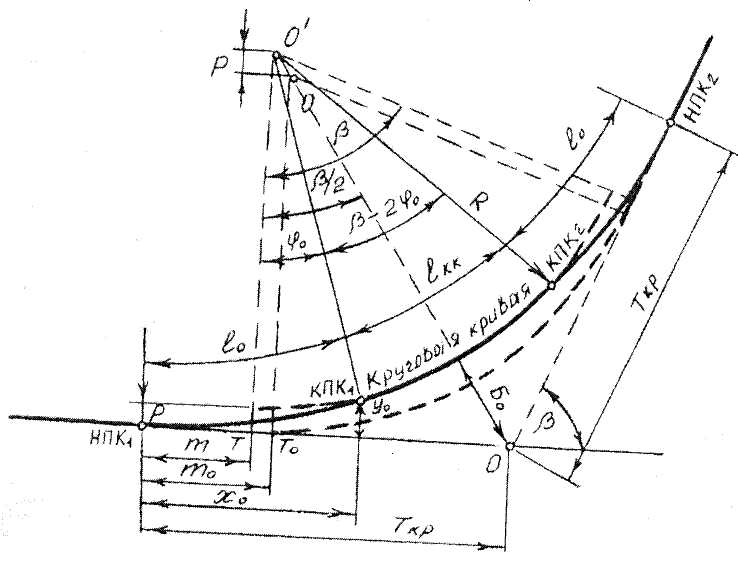
Сочетание круговой кривой с переходными. На рис. 15.6 показана кривая, поворачивающая трассу на угол a и состоящая из круговой части с радиусом R и двух переходных кривых одинаковой длины l.

Рис. 15. 5 Смещение начала переходной кривой

Рис. 15.6 Сопряжение круговой кривой

Если бы не было переходных кривых, в образованный прямыми линиями трассы угол была бы вписана дуга окружности радиуса R, равная Q-СК-Q₁ и имеющая длину K = Ra.

При наличии переходных кривых на каждой из них происходит поворот трассы на угол b, отчего на долю круговой кривой приходится поворот на угол a-2b. Поэтому суммарная длина кривой равна

Тангенс и биссектриса определяются по формулам:

Домер в этом случае равен

.

В полевых условиях значения m, Т_p и Б_p вычисляют на микрокалькуляторе или выбирают из таблиц для разбивки кривых на железных дорогах. Пикетажное положение главных точек кривой вычисляют по формулам, аналогичным (15.3) и (15.4).

Источник

Переходная кривая

Перехо́дная крива́я (ПК) — элемент плана дороги, которым сопрягаются путевые прямые с круговыми кривыми и круговые кривые между собой.

Содержание

Предназначение

Переходная кривая используется для того, чтобы кривизна трассы изменялась плавно, а не скачкообразно в месте сопряжения элементов пути с разной кривизной (прямая и круговая кривая, круговые кривые разных радиусов или направленные в разные стороны в виде буквы S (обратные кривые)). При резком изменении кривизны пути поперечные силы, действующие на транспортное средство, изменяются скачкообразно, что приводит к повышенному динамическому воздействию на дорогу (путь) и экипажную часть, увеличивая их износ, повышает вероятность вылета за пределы дороги (схода с рельсов) или опрокидывания транспортного средства и вызывает дискомфорт у пассажиров.

Особенно важно устройство переходных кривых при высоких скоростях движения, применении путевых кривых малого радиуса, тяжёлом подвижном составе, пропуске длиннобазового подвижного состава (особенно ПС с длинной жёсткой базой, например паровозов).

Расчёт переходной кривой

Переходную кривую рассчитывают таким образом, чтобы в своём начале она имела кривизну, равную нулю (как у прямой, то есть начало кривой является точкой перегиба), а потом плавно меняла кривизну, в конце достигая значения, обратного радиусу круговой кривой (и наоборот для схода с виража). Поскольку переходная кривая является частью виража, на ней обеспечивается нарастающий поперечный уклон дорожного полотна (подъём внешнего рельса на рельсовых дорогах) до уровня, равного уклону на круговой кривой (и наоборот для схода с виража).

В качестве переходных чаще всего применяют следующие кривые:

Источник

Переходные кривые. Назначение. Проектирование закругления с переходной кривой

Переходные кривые предназначены для постепенного нарастания центробежной силы при переходе автомобиля с прямой на круговую кривую.

R переходной кривой – переменный. Изменяется от бесконечности до R в конце.

В конце переходной кривой ρ=R, а S=L:

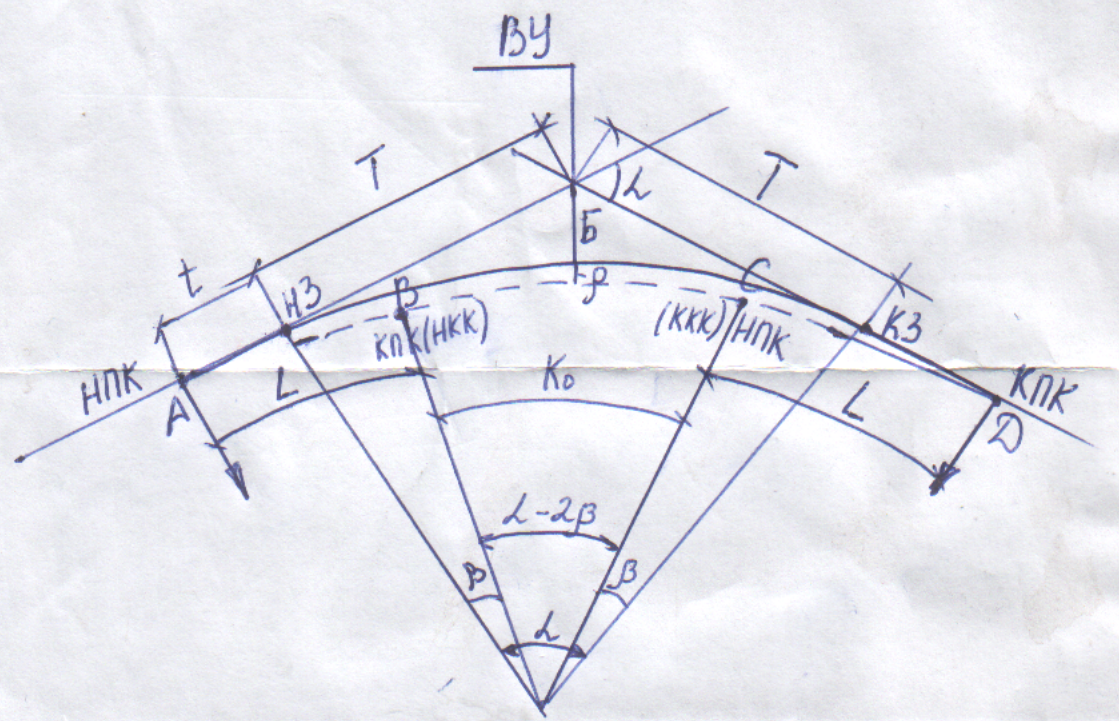
Пусть трасса а/д (ось а/д) на ВУ поворачивает на угол α при отсутствии переходных кривых, закругление с круговой кривой начинается и заканчивается от ВУ на расстоянии =Т

При введении переходной кривой L начало закругления (т. А) и конец закругления (т. Д) смещаются от Т на величину t=0,5L

Переходная кривая L на круговую кривую на угол β

Круговая кривая КО смещается к центру на сдвижку р от положения круговой кривой. Длина её

Последовательность проектирования закругления с переходной кривой.

1 Вычисляется min значение длины переходной кривой L по условиям удобства движения

2 Проверяется возможность разбивки закругления с переходной кривой

α>=2β,если α=2β,то К₀=0 и закругление состоит из 2 кривых и называется клотоидным

3 Определяется пикетное положение основных точек закругления АВСД

4 Вычисляют координаты для детальной выноски закругления на местность в системе X₁Y₁до середины закругления и X₂Y₂ после

Источник