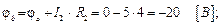Потенциальная диаграмма

Потенциальной диаграммой замкнутого контура называется графическая интерпретация распределения электронного потенциала вдоль замкнутого контура в зависимости от входящих в него сопротивлений.

Потребитель энергии отображается на электрической схеме как резистор с заданным сопротивлением R. Если такое элемент присутствует в участке цепи, то изменение потенциалов на концах участка будет соответствовать падению напряжения на этом резисторе.

Если на участке цепи присутствует источник напряжения, то на концах такого участка также будет наблюдаться разность потенциалов, численно равная ЭДС источника.

Построение потенциальной диаграммы

Для построения потенциальной диаграммы, замкнутый контур разбивается на участки таким образом, чтобы каждый из них содержал только одного потребителя или один источник электроэнергии.

Потенциальная диаграмма строится в декартовой системе координат, где по оси абсцисс откладывается, с соблюдением масштаба, сопротивление участков цепи, а по оси ординат – потенциалы точек. Точки замкнутого контура и сопротивления элементов откладываются (отмечаются на диаграмме) в той последовательности, в которой они встречаются при обходе контура.

В начало координат диаграммы помещается точка, потенциал которой условно выбран нулевым.

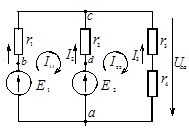
Демонстрацию алгоритма и правил построения потенциальной диаграммы выполним на примере замкнутого контура abcdef (точки a и f совпадают), представленного на рисунке 1. Положительное направление обхода контура – по часовой стрелке. Для расчетов примем:

Замкнутый контур разбит на участки, каждый из которых содержит либо источник ЭДС, либо резистор.

Примем нулевым потенциал точки а

Следующая точка согласно выбранному направлению движения – b. На участке ab находится источник ЭДС E₁. Так как движение на данном участке происходит от отрицательного полюса источника к положительному (направление обхода контура совпадает со стрелкой источника ЭДС), то значение потенциалы на участке повысится на величину E₁:

Следующий рассматриваемый участок – bc. На нем происходит уменьшение потенциала на величину падения напряжения на резисторе R1.

Аналогичные процессы происходят на участках cd и de. Следовательно,

На участке ef находится еще один источник ЭДС E₂. Движение по данному участку реализуется от отрицательного полюса к положительному, следовательно потенциал повысится на величину E₂

Если направление обхода контура не совпадает с направлением ЭДС, тогда ЭДС записывают со знаком минус

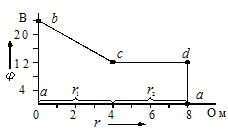
На основании полученных данных можно построить потенциальную диаграмму (рисунок 2).

Рис. 2. Потенциальная диаграмма

По потенциальной диаграмме легко можно найти разность потенциалов между любыми точками электрической цепи.

Источник

Что такое потенциальная диаграмма как она строится?

Какие электрические цепи называются линейными?

Линейной электрической цепью называют такую цепь, все компоненты которой линейны. К линейным компонентам относятся зависимые и независимые идеализированные источники токов и напряжений, резисторы (подчиняющиеся закону Ома), и любые другие компоненты, описываемые линейными дифференциальными уравнениями, наиболее известны электрические конденсаторы и индуктивности.

Сформулируйте законы Кирхгофа. Что отражают они физически?

Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

Физический смысл второго закона Кирхгофа

Второй закон устанавливает связь между падением напряжения на замкнутом участке электрической цепи и действием источников ЭДС на этом же замкнутом участке. Он связан с понятием работы по переносу электрического заряда. Если перемещение заряда выполняется по замкнутому контуру, возвращаясь в ту же точку, то совершенная работа равна нулю. Иначе бы не выполнялся закон сохранения энергии. Это важное свойство потенциального электрического поля описывает 2 закон Кирхгофа для электрической цепи.

Физический смысл первого закона Кирхгофа

Первый закон устанавливает связь между токами для узлов электрической цепи. Он вытекает из принципа непрерывности, согласно которому суммарный поток зарядов, образующих электрический ток, проходящих через любую поверхность равен нулю. Т.е. количество прошедших зарядов в одну сторону равно количеству зарядов, прошедших в другую сторону. Т.е. количество зарядов никуда не может деться. Они не могу прост исчезнуть.

Сколько уравнений составляется по первому закону Кирхгофа и сколько по второму?

Кол-во уравнений, первый закон Кирхгофа = Кол-во узлов – 1

Кол-во уравнений, второй закон Кирхгофа = Кол-во ветвей – Кол-во узлов + 1

Понятие независимого контура. Чему равно число независимых контуров в любой цепи?

Понятия узел, ветвь, электрическая цепь.

Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы (рис. 1, 2), введя понятие ветви и узла.

Ветвью называется участок цепи, обтекаемый одним и тем же током.

Узел – место соединения трех и более ветвей.

Что такое потенциальная диаграмма как она строится?

Источник

Расчет потенциальной диаграммы

Содержание:

Потенциальная диаграмма

Пример:

Построим потенциальную диаграмму для внешнего контура электрической цепи, схема которой изображена на рис. 2. При построении диаграммы используем значения токов, рассчитанные в примере 2. Обход контура выбираем по часовой стрелке.

В результате расчета потенциал точки 3 оказался выше потенциала точки 4, так как выбранное на схеме направление тока противоположно его истинному направлению.

Аналогично определим потенциал точки 5: Потенциал точки I выше потенциала точки 5 на величину ЭДС Е1, так как направление обхода контура совпадает с направлением ЭДС (переход от отрицательного зажима источника ЭДС к его положительному зажиму), следовательно

Аналогичным образом определяются потенциалы точек 2 и 4:

Расчет потенциала точки 4 выполнен для проверки вычислений. Суммарное сопротивление резисторов контура

Зная максимальное и минимальное значения потенциалов точек и суммарное сопротивление резисторов контура, можно выбрать масштабы для потенциалов и сопротивления, а затем построить потенциальную диаграмму (рис. 3).

Возможно вам будут полезны данные страницы:

По потенциальной диаграмме можно определить потенциал любой точки контура, эквипотенциальные точки контура, а также разность потенциалов (напряжение) между любыми точками контура. Для определения напряжения заданные точки проецируются на ось ординат; умножив отрезок между проекциями точек на масштаб по напряжению, получим разность потенциалов.

По диаграмме можно определить величину и направление тока на любом участке контура. Ток пропорционален тангенсу угла наклона к оси абсцисс отрезка диаграммы, соответствующего рассматриваемому участку. Направление тока определяется знаком угла наклона; угол, отсчитываемый по часовой стрелке, считается положительным.

Расчет и построение потенциальной диаграммы

Обозначим на схеме рис. 6 реальные направления токов и ЭДС внешнего контура. Примем потенциал точки (1) равным нулю, т.с.

Рассчитаем потенциалы всех точек, обходя контур по часовой стрелке (рис. 6).

Замечание. Источник тока учтен при расчете тока . Поэтому в схему рис.6 ЭДС не включаем.

Выберем масштаб по напряжению и сопротивлению:

Рис. 7. Потенциальная диаграмма для замкнутого внешнего контура заданной схемы

Потенциальная диаграмма

Пример построения потенциальной диаграммы

Условия расчета

Построить потенциальную диаграмму для контура цепи, изображенной на рисунке 4.5.2.1.

Схема контура цепи

Данные для расчета потенциальной диаграммы

Токи найдены в предварительных расчетах всей цепи.

Расчет потенциальной диаграммы

Точку f заземлим, т.е. примем потенциал этой точки равным нулю, . При построении потенциальной диаграммы эту точку поместим в начало координат (см. рисунок 10.1.5.1).

Обход контура принимаем по направлению движения часовой стрелки, начиная с точки f

Подсчитываем потенциалы отдельных точек контура

Суммарное сопротивление контура:

Построение потенциальной диаграммы

Выбираем масштабы сопротивлений и потенциалов:

По полученным данным (п. 10.1.4) строим потенциальную диаграмму (см. рисунок 10.1.5.1) контура , изображенного на рисунке 10.1.2.1.

Чем больше ток в том или ином пассивном участке цепи, тем круче получается соответствующий участок диаграммы. Тангенсы углов наклона к оси абсцисс пропорциональны соответствующим токам, например,

Потенциальная диаграмма позволяет найти напряжение между любыми точками на схеме. Это напряжение равно разности ординат соответствующих точек диаграммы. Например, (см. рисунок 10.1.5.1).

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Потенциальная диаграмма электрической цепи

Потенциальной диаграммой называется графическое изображение распределения электрического потенциала вдоль замкнутого контура в зависимости от сопротивления участков, входящих в выбранный контур.

Для построения потенциальной диаграммы выбирают замкнутый контур. Этот контур разбивают на участки таким образом, чтобы на участке находился один потребитель или источник энергии. Пограничные точки между участками необходимо обозначить буквами или цифрами.

Произвольно заземляют одну точку контура, её потенциал условно считается нулевым. Обходя контур по часовой стрелке от точки с нулевым потенциалом, определяют потенциал каждой последующей пограничной точки как алгебраической суммы потенциала предыдущей точки и изменения потенциала между этими соседними точками.

Изменение потенциала на участке зависит от состава цепи между точками. Если на участке включен потребитель энергии (резистор), то изменение потенциала численно равно падению напряжения на этом резисторе. Знак этого изменения определяют направлением тока. При совпадении направлений тока и обхода контура знак отрицательный, в противном случае он положительный.

Если на участке находится источник ЭДС, то изменение потенциала здесь численно равно величине ЭДС данного источника. При совпадении направления обхода контура и направления ЭДС изменение потенциала положительно, в противном случае оно отрицательно.

После расчета потенциалов всех точек строят в прямоугольной системе координат потенциальную диаграмму. На оси абсцисс откладывают в масштабе сопротивление участков в той последовательности, в которой они встречались при обходе контура, а по оси ординат – потенциалы соответствующих точек. Потенциальная диаграмма начинается с нулевого потенциала и заканчивается после обхода контура таковым.

Построение потенциальной диаграммы электрической цепи

В данном примере потенциальную диаграмму строим для первого контура цепи, схема которой изображена на рисунке 1.

Рис. 1. Схема сложной электрической цепи

В рассматриваемый контур входят два источника питания E1 и E2, а также два потребителя энергии r1, r2.

Следующей точкой на пути обхода контура будет точка b. На участке ab находится источник ЭДС Е1. Так как на данном участке мы идем от отрицательного полюса источника к положительному, то потенциал повышается на величину Е1 :

При переходе от точки b к точке c происходит уменьшение потенциала на величину падения напряжения на резисторе r1 (направление обхода контура совпадает с направлением тока в резисторе r1) :

При переходе к точке d потенциал возрастает на величину падения напряжения на резисторе r2 (на этом участке направление тока встречно направлению обхода контура) :

φ d = φ c + I2r2 = 12 + 0 х 4 = 12 В

Потенциал точки а меньше потенциала точки d на величину ЭДС источника E2 (направление ЭДС встречно направлению обхода контура) :

Результаты расчета используют для построения потенциальной диаграммы. На оси абсцисс откладывают сопротивление участков в той последовательности, как они встречаются при обходе контура от точки с нулевым потенциалом. Вдоль оси ординат откладывают рассчитанные ранее потенциалы соответствующих точек (рисунок 2 ).

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Потенциальная диаграмма

Для наглядного отображения распределения потенциалов в электрической цепи постоянного тока используется графическое представление в виде потенциальной диаграммы. Потенциальная диаграмма представляет собой график распределения потенциала вдоль участка цепи или контура, при этом по оси абсцисс откладываются нарастающим порядком сопротивления резистивных элементов, встречающихся на пути обхода ветви или контура, а по оси ординат – потенциалы соответствующих точек. Таким образом, каждой точке рассматриваемого участка или контура соответствует точка на потенциальной диаграмме (точка не обязательно должна соответствовать одному из узлов схемы, это просто место соединения двух элементов).

Потенциал любой точки электрической цепи может быть вычислен через потенциал предыдущей точки и падение напряжения на элементе, включенном между рассматриваемой точкой и предыдущей. Если между этими точками расположен источник ЭДС, то величина ЭДС берется со знаком плюс, если источник направлен к рассматриваемой точке, иначе – со знаком минус:

Если между этими точками расположен резистор, то падение напряжения на нем берется со знаком плюс, если протекающий через него ток направлен к предыдущей точке, иначе – со знаком минус:

Рассмотрим построение потенциальной диаграммы на примере схемы рис. 1.6.

При параметрах схемы Е₁ = 48В, Е₂ = 37 В, R₁ = 5 Ом, R₂ = 4 Ом, R₃ = 3 Ом, R₄ = 1 Ом токи в ветвях схемы равны: I₁ = 10 A, I₂ = –5 A, I₃ = –2 A.

Построим потенциальную диаграмму для контура abcda. Для выбора масштаба по горизонтальной оси просуммируем сопротивления резисторов вдоль рассматриваемого контура (если в условии задач не указаны внутренние сопротивления источников, то они считаются нулевые для источников ЭДС и равные бесконечности для источников тока):

Рис. 1.6. Резистивная цепь

Потенциалы точек контура вычислим относительно потенциала точки a, потенциал которой принят за нуль:

Таким образом, координаты точек потенциальной диаграммы: а(0; 0); b(4; –20); c(4; 17); d(7; 2); а(8; 0). С учетом выбранных масштабов на рис. 1.7 построена потенциальная диаграмма для контура abcda.

Рис. 1.7. Потенциальная диаграмма

Дата добавления: 2015-04-16 ; просмотров: 11 ; Нарушение авторских прав

Источник