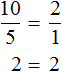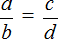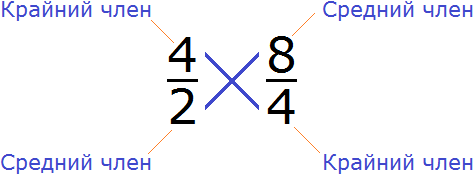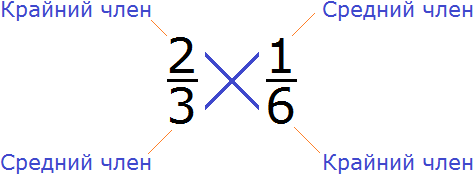Для чего нужна пропорция

Что такое пропорция

Что такое пропорция

Пропорция — это равенство двух отношения.

Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.

Пропорция всегда содержит равные коэффициенты.

Если выразить определение формулой, то выглядеть оно будет так:

a и d — крайние члены пропорции, b и с — средние члены пропорции.

Читается это выражение так: a так относится к b, как c относится к d

Например:

Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.

15 и 3 — крайние члены пропорции.

5 и 9 — средние члены пропорции.

Наглядный пример для понимания:

У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.

Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!

А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.

Что мы имеем: 4 кусочка и 2 друга, претендующих на них.

Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.

Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.

Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным😉

Основное свойство пропорции

Запомните основное свойство пропорции:

Произведение крайних членов пропорции равно произведению средних членов этой пропорции.

В виде формулы свойство выглядит так:

a : b = c : d
a * d = b * c

Мы знаем, что a и d — крайние члены пропорции, b и c — средние.

Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.

Давайте проверим несколько пропорций.

Пример 1. Дана пропорция:6/2 = 12/4

Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.

Пример 2. Дана пропорция: 10/2 = 16/4

Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Примеры решения задач с пропорцией

Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.

Задачка 1. Дана математическая пропорция: 15/3 = x/4

Ответ: в пропорции 15/3 = x/4, x = 20

Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.

Ответ: четвертый член пропорции — 12.

Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?

Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.

Задачка 4. Дана пропорция: 20/2 = y/4

Источник

Пропорция

Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.

Что такое пропорция?

Пропорцией называют равенство двух отношений. Например, отношение равно отношению

Данная пропорция читается следующим образом:

Десять так относится к пяти, как два относится к одному

Дроби, из которых составлена пропорция, всегда равны. Например, если в пропорции 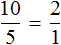выполнить деление в обеих дробях, то получится число 2 в обеих частях:

Предположим, что в классе 10 девочек и 5 мальчиков

Запишем отношение десяти девочек к пяти мальчикам:

Преобразуем данное отношение в дробь

Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки

Теперь рассмотрим другой класс в котором две девочки и один мальчик

Запишем отношение двух девочек к одному мальчику:

Преобразуем данное отношение в дробь:

Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:

В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.

Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам

а также отношение 12 девочек к 2 мальчикам

Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что 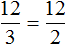, поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.

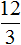
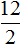
Поэтому отношение не пропорционально отношению .

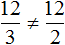
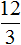
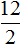
Вторая рассмотренная нами пропорция была . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями и знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.

Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2

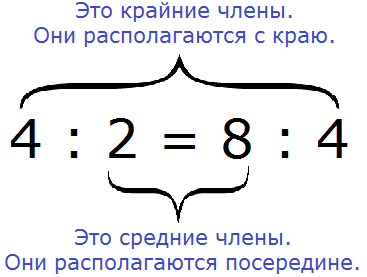
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.

В нашей пропорции 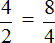крайние члены это 4 и 4, а средние члены это 2 и 8

Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:

Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:

С помощью переменных пропорцию можно записать так:

Данное выражение можно прочесть следующим образом:

a так относится к b, как c относится к d

Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.

Основное свойство пропорции

Основное свойство пропорции выглядит следующим образом:

Произведение крайних членов пропорции равно произведению её средних членов.

Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.

Например, проверим правильно ли составлена пропорция 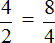. Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:

4 × 4 = 16 — произведение крайних членов пропорции равно 16.

2 × 8 = 16 — произведение средних членов пропорции так же равно 16.

4 × 4 = 2 × 8

4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция 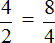составлена правильно.

Пример 2. Проверить правильно ли составлена пропорция

Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:

2 × 6 = 12 — произведение крайних членов пропорции равно 12

3 × 1 = 3 — произведение средних членов пропорции равно 3

2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция 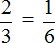составлена неправильно.

Поэтому в пропорции 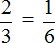разумнее заменить знак равенства (=) на знак не равно (≠)

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник

Урок математики по теме «Пропорция вокруг нас». 6-й класс

Класс: 6

Презентация к уроку

Тип урока: урок обобщения

Оборудование: компьютер, интерактивная доска.

I. Организационный момент:

1) сообщение темы урока (слайд 1);

2) сообщение целей и задач урока.

III. Из истории пропорции. (слайды 2-5)

Слово “пропорция” происходит от латинского слова proportio, означающего соразмерность, определенное соотношение частей между собой. Пропорции используют с древности при решении разных задач в математике.

Ещё в древней Греции математики использовали такой аппарат, как ПРОПОРЦИЯ.

Пропорцией называют равенство отношений двух или нескольких пар чисел или величин.

В Вавилоне с помощью пропорций рисовали планы древних городов. На рисунке изображен найденный при раскопках план древнего вавилонского города Ниппура. Когда ученые сравнили результаты раскопок города с этим планом, оказалось, что он сделан с большой точностью.

IV. Практическое применение пропорций. (слайд 6-7)

Математика применяется практически во всех сферах жизни человека. И в повседневной жизни мы используем математические навыки, в том числе и пропорцию.

1. Архитектура (слайды 8-11)

При постройке храма в честь богини Дианы римляне взяли пропорцию, которой отличаются стройные женщины: толщина колоны составила лишь 1/8 ее высоты. Благодаря этому колонны казалась выше, чем она была на самом деле,как раз за счет уменьшения толщины. В архитектуру вошли оба вида колонн, сохраняющие одна мужскую, другая женскую пропорции в отношениях между основанием и высотой.

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамонасвидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

1. На строительство дома идет 4 тыс. штук кирпича. Сколько тысяч штук кирпича необходимо для строительства 15 таких же домов.

2. Для перевозки песка при строительстве потребовалось 14 автомашин грузоподъемностью 4,5 т. Сколько потребуется автомашин грузоподъемностью 7 т для перевозки этого же песка?

2. Кулинария (слайды 12-13)

Понятие пропорции используется в кулинарии. Когда мы готовим какое-либо блюдо, мы стараемся использовать то количество продуктов, которое указано в поварской книге. Это делается для того, чтобы не испортить блюдо. Если мы возьмём больше соли, то пересолим, а если меньше, то будет не вкусно. Ещё пропорция позволяет рассчитать количество продуктов для приготовления одного и того же блюда для разного числа гостей.

3. Для приготовления варенья из 2 кг крыжовника необходимо 3 кг сахара. Сколько кг сахара необходимо для приготовления варенья из 4,4 кг крыжовника.

4. При сушке масса яблок изменилась с 20 кг до 18,2 кг. На сколько % уменьшилась масса яблок при сушке?

3. Медицина(слайды 14-16)

5. Для лекарственного отвара ромашки на 100 г кипятка необходимо 20 г сухой ромашки. Сколько г ромашки необходимо для 500г отвара.

6. Больному прописан курс лекарства, которое нужно принимать по 250 мг два раза в день в течение 7 дней. В одной упаковке лекарства содержится 10 таблеток по 125 мг. Какое наименьшее количество упаковок понадобится на весь курс лечения.

4. Химия (слайды 17-19)

Заслуженное место заняла теория пропорций при решении задач по химии.

Например. Какова процентная концентрация раствора, полученного растворением 5 г поваренной соли в 45 г воды?

7. В 2,4 л воды растворили 100 г соли. Какова концентрация полученного раствора?

8. Имеется 90 г 80% уксусной эссенции. Какое наибольшее количество 9% столового уксуса из нее можно получить?

5. Технология (слайды 20-23)

На уроках технологии мы также используем пропорцию. Когда мы хотим сшить какую-либо вещь меньшего или большего размера, мы уменьшаем или увеличиваем выкройку до нужного нам размера. Например, выкройка фартука на себя и на куклу. Размеры элементов кукольного фартука отличаются от соответствующих размеров моего фартука в одно и тоже число раз.

9. Краеобметочная машина 0,6 м ткани обрабатывает за 2,16 мин. Сколько метров можно обметать за 1,44 мин?

10. На изготовление детского платья идет 1,2 м. Сколько необходимо ткани на платье для взрослых, если расход на него на 40 % больше.

6. Физика.(слайды 24-25)

С глубокой древности люди пользовались различными рычагами. Весло, лом, весы, ножницы, качели, тачка и т.д. – примеры рычагов. Выигрыш, который дает рычаг в прилагаемом усилии, определяется пропорцией, где M и m – массы грузов, а L и l – “плечи” рычага.

11. По правилу рычаганайти М, если l=2 м, L=8 м, m=4 кг.

12. В городе Жуковском на авиа-шоу МАКС проходят показательные полёты самолётов. Такому самолёту-истребителю, как МИГ-29 на 3 часа полётов требуется около 7,5 тонн керосина. Сколько тонн керосина потребуется МИГ-29 на 7 часов полётов?

7. Моделирование.(слайды 26-27)

13. Длина модели автомашины 42см.Какова длина автомобиля, если размеры его уменьшены в 10000 раз.

14. На модель парусника идет 60 см ткани. Сколько м ткани необходимо для изготовления трех таких же парусника.

8. География. (слайды 28-30)

В географии также применяют пропорцию – масштаб. Масштабом называют отношение длины отрезка на карте или плане к длине соответствующего отрезка на местности. Масштаб показывает во сколько раз расстояние на плане меньше, чем указанное расстояние на самом деле.

15. Найдите расстояние от Москвы до Северного полюса, если на карте это расстояние – 3,5 см, а М 1:100000000.

16. Найти расстояние на карте между городами Ростов –на –Дону и Москвой, если расстояние между ними 1200 км, а М 1:50000000.

V. Сообщения учеников о применении пропорции.

9. Изобразительное искусство. (слайды 30-37)

10. Биология.(слайды 38-39)

11. Музыка.(слайды 40-41)

12. Литература.(слайды 42-44)

С глубокой древности люди используют математический аппарат в повседневной жизни. Одним из них является пропорция. Она используется, начиная с приготовления пищи и заканчивая произведениями искусства, такими как скульптура, живопись, архитектура, а также в живой природе.

Источник

Презентация на тему «Пропорция в жизни человека» (Исследовательская работа по математике 6 класс)

Описание презентации по отдельным слайдам:

Из истории изучения пропорции Пропорции начали изучать еще в древности. В 4 веке до н.э. древнегреческий математик Евдокс дал определение пропорции, составленной из величин любой природы. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке. Слово «пропорция» ввел в употребление Цицерон в 1 веке до н.э., который буквально означал аналогия, соотношение.

Теория отношений и пропорций была подробно изложена в «Началах» Евклида (III век до нашей эры), там, в частности, приводится и доказательство основного свойства пропорции. Оно звучит так: «В верной пропорции произведение крайних членов равно произведению средних. a : b = c : d крайние средние

Виды пропорций В математике различают два типа пропорций: Случайные (например, отношение или пропорции между числом слогов самых длинных и самых коротких названия населённых пунктов. ) Закономерные (например, пропорция между длительностью нот). «Закономерные» отношения Прямо пропорциональны Обратно пропорциональные широко используются в разнообразнейших расчетах,производимых школьниками,инженерами,администраторами и т.д Прямо прпорциональные величины : длина окружности и ее радиус; размеры предметов и размеры отбрасываемых ими теней; Обратно пропорциональные величины: продолжительность звучание одного такта, и число тактов используемых за одну минуту;

ЗОЛОТОЕ СЕЧЕНИЕ В искусстве чаще других встречается пропорция, получившая название «золотое сечение». Золотым сечением и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длинна всего отрезка так относится к длине его большей части, как длинна большей части к меньшей. Приближенно это отношение равно 0, 618 ≈5/8. Золотое сечение чаще всего применяется в произведениях искусства, архитектуре, встречается и в природе.

Применение пропорции пропорция медицина кулинария география русский язык биология физика Изобразительное искусство технология Сельское хозяйство черчение

Пропорции на уроках технологии Размеры элементов кукольного сарафана отличаются от соответствующих размеров сарафана девушки в одно и тоже число раз. Задача : Длина изделия на выкройке 75см. Вычислите масштаб чертежа, если на нем длина сарафана будет равна 15см. Ответ 1:5.

Пропорции в физике С глубокой древности люди пользовались различными рычагами. Весло, лом, весы, ножницы, качели, тачка и т.д. – примеры рычагов. Выигрыш, который дает рычаг в прилагаемом усилии, определяется пропорцией, где M и m – массы грузов, а L и l – «плечи» рычага.

Биология Рассматривая расположение листьев на общем стебле растений, можно заметить, что между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (точка В).

Русский язык В русском языке встречаются пословицы и поговорки, устанавливающие прямую и обратную зависимость. Например: 1) Как аукнется, так и откликнется. 2) Чем выше пень, тем выше тень. 3) Когда гнев впереди- ум позади. 4) Когда карман сух, тогда и суд глух.

Пропорция в архитектуре Пропорции золотого сечения создают впечатление гармонии, красоты. Поэтому скульпторы, архитекторы, художники использовали и используют золотое сечение в своих произведениях. Золотые пропорции присутствуют в размерах фасада древнегреческого храма Парфенона, Собора Василия Блаженного, Собора на Нерли и многих других шедеврах архитектуры.

Занимательная пропорция Благодаря знаниям по теме «Пропорция» удалось смастерить подобие Земного шара – глобус. К числу вещей, которые никак нельзя изобразить на бумаге, принадлежит точный план нашей Солнечной системы.

Заключение С глубокой древности люди используют математические знания в повседневной жизни. Одним из них является пропорция. Она используется, начиная с приготовления пищи и заканчивая произведениями искусства, такими как скульптура, живопись, архитектура, а также в живой природе. Пропорции сопровождают нас повсюду и являются неотъемлемой частью нашей жизни. В своей работе я привела только не большой перечень сфер где применяют пропорции. На самом деле этот список намного больше. Ведь пропорции появились одновременно с природой, даже до появления человека.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-631122

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Зарплаты педагогов Ростовской области вырастут в среднем на 10-15%

Время чтения: 2 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Чем заняться с детьми в новогодние праздники в Москве

Время чтения: 4 минуты

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

При детском омбудсмене в России создадут платформу для взаимодействия с родителями

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник