Для чего нужна система координат
Система координат
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.
В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.
В географии координаты — широта, долгота и высота над известным общим уровнем (например, океана). См. географические координаты.
В астрономии координаты — величины, при помощи которых определяется положение звезды, например, прямое восхождение и склонение.
Небесные координаты — числа, с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой систему полярных координат на сфере с соответствующим образом выбранным полюсом. Систему небесных координат задают большим кругом небесной сферы (или его полюсом, отстоящим на 90° от любой точки этого круга) с указанием на нём начальной точки отсчёта одной из координат. В зависимости от выбора этого круга системы небесных координат называлась горизонтальной, экваториальной, эклиптической и галактической.
Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.
Содержание
Список наиболее распространённых систем координат
Основные системы
В этом разделе даются разъяснения к наиболее употребляемым системам координат в элементарной математике.
Декартовы координаты
Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел 
В пространстве же необходимо уже 3 координаты 
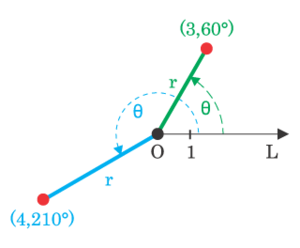
Полярные координаты
В полярной системе координат положение точки определяется расстояние до центра координат и углом радиус-вектора с осью Ox.
Термин «полярные координаты» используется только на плоскости, в пространстве применяются цилиндрические и сферические системы координат.
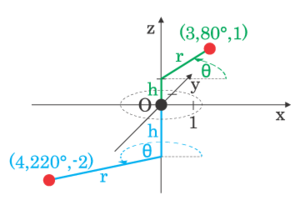
Цилиндрические координаты
Цилиндрические координаты — трехмерный аналог полярных, в котором точка P представляется трехкомпонентным кортежем 
Полярные координаты имеют один недостаток: значение θ теряет смысл, если r = 0.
Цилиндрические координаты полезны для изучения систем, симметричных вокруг некой оси. Например, длинный цилиндр в декартовых координатах имеет уравнение 
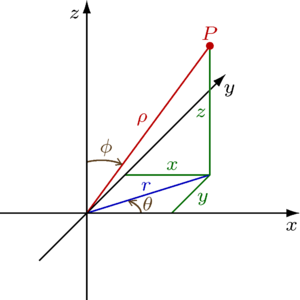
Сферические координаты
Сферические координаты — трехмерный аналог полярных
Обозначения, принятые в Америке
В сферической системе координат, расположение точки P определяется тремя компонентами: 
Сферическая система координат также имеет недостаток: φ теряет смысл если ρ = 0, также и θ теряет смысл, если ρ = 0 или φ = 0 или φ = 180°.
Для построения точки по её сферическими координатами, нужно: от полюса отложить отрезок, равный ρ вдоль положительной z-оси, вернуть его на угол φ вокруг оси y в направлении положительной x-оси, и вернуть на угол θ вокруг z-оси в направлении положительной y-оси.
Сферические координаты полезны при изучении систем, симметричных вокруг точки. Так, уравнение сферы в декартовых координатах выглядит как 

Европейские обозначения
В Европе принято использовать другие обозначения. Положение точки задаётся числами: 


Переход из одной системы координат в другую
Декартовы и полярные



Координаты. Системы координат. Название МСК по регионам
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве.
Общие сведения о системах координат
Система координат — это комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. В общем и целом систему координат можно определить как опорную систему для определения положения точек в пространстве или на плоскостях и поверхностях относительно выбранных осей, плоскостей или поверхностей.
Систему координат широко применяют во многих отраслях науки:
В географии координаты выбираются как (приближённо) сферическая система координат — широта, долгота и высота над известным общим уровнем (например, океана).
В астрономии небесные координаты — упорядоченная пара угловых величин (например, прямое восхождение и склонение), с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой сферическую систему координат (без радиальной координаты) с соответствующим образом выбранной фундаментальной плоскостью и началом отсчёта. В зависимости от выбора фундаментальной плоскости система небесных координат называется горизонтальной (плоскость горизонта), экваториальной (плоскость экватора), эклиптической (плоскость эклиптики) или галактической (галактическая плоскость).
Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.
Что такое координатная сетка?
Одним из элементов географической карты является сетка координатных линий. Существуют два вида координатной сетки: картографическая, образуемая линиями меридианов и параллелей, и сетка прямоугольных координат, образуемая линиями, параллельными осям координат OX и OY.
На топографических картах меридианы и параллели являются границами листа карты; в углах карты подписываются их долгота и широта. Внутри листа вычерчивается сетка прямоугольных координат в виде квадратов, называемая иногда километровой сеткой, так как на картах масштаба 1:10 000 и мельче линии сетки проводятся через целое число километров.
Вертикальные линии сетки параллельны осевому меридиану зоны (оси OX) и имеют уравнение Y = Const; значение координаты Y подписывается у каждой линии. Горизонтальные линии сетки параллельны оси OY и имеют уравнение X = Const; значение координаты X подписывается у каждой линии.
Для удобства пользования листами карт, на которых изображены граничные участки зоны, на них показывается сетка прямоугольных координат соседней зоны. Ширина граничной полосы с сеткой соседней зоны составляет 2 градуса по долготе с обоих сторон зоны. Выходы линий координатной сетки соседней зоны наносятся на внешнюю сторону рамки листа карты.
Классификация систем координат
1. Прямоугольная (плоская) система координат: XY
За основную плоскость XOY в данном случае принята плоскость земного экватора. Основная координатная ось OX направлена в определенную точку. Ось OY расположена в плоскости земного экватора под углом 90º к востоку от принятого начального меридиана. Ось OZ совмещена с северным направлением оси вращения Земли.
2. Пространственная прямоугольная система координат: XYZ
Начало пространственных прямоугольных координат либо определяется под условием совмещения с центром масс Земли (в общеземных системах), либо находится вблизи от него.
Ориентировка оси Z в каждой системе координат выполняется с учетом ориентировки средней оси вращения Земли. При установлении системы среднего полюса, в том числе и полюса в Системе МУН, не накладывают условия прохождения средней оси вращения через центр масс Земли, поэтому и в референцных и в общеземных системах оси Z не совпадают со средней осью вращения, а параллельны ей.
Плоскость XOY перпендикулярна оси Z и средней оси вращения Земли. Плоскость XOZ выбирается под условием ее параллельности плоскости начального астрономического меридиана.
3. Геодезическая (эллипсоидальная) система координат: BLH
Геодезическая эллипсоидальная система координат строится на базе эллипсоида вращения, поверхность которого используется в качестве поверхности относимости, на которую проецируются и затем обрабатываются результаты геодезических измерений.
B– геодезическая широта, угол между нормалью к эллипсоиду, проведенной через заданную точку M на поверхности Земли, и плоскостью экватора;
L – геодезическая долгота, двугранный угол между плоскостями гринвичского G и заданного геодезического меридианов;
H – геодезическая высота над референц-эллипсоидом, расстояние по нормали от поверхности эллипсоида до точки M.
Назначение систем координат
1. Общеземные (мировые ) WGS 84, ПЗ 9011, ITRS
Общеземными принято называть такие системы координат, которые получены под условием совмещения их начала с центром масс Земли. Они устанавливаются в отношении территории, покрывающей весь земной эллипсоид. И используется для решения общеземных задач. Наиболее удобными являются географические координаты (широта и долгота) отсчитываемые от поверхности экватора и начального меридиана в виде дуг, которым соответствуют центральные углы.
2. Государственные (СК-95, СК-63, ГСК-2011)
Эта система координат ограничивается территорией одного государства и используется, для осуществления геодезических и картографических работ внутри этого государства. В РФ в качестве координатной поверхности в этой системе используется поверхность эллипсоида Красовского.
3. Местные (МСК-50, МСК-50.2, Московская)
Под местной системой координат понимается условная система координат, устанавливаемая в отношении ограниченной территории, не превышающей территорию субъекта Российской Федерации, начало отсчета координат и ориентировка осей координат которой смещены по отношению к началу отсчета координат и ориентировке осей координат единой государственной системы координат, используемой при осуществлении геодезических и картографических работ. Местные системы координат устанавливаются для проведения геодезических и топографических работ при инженерных изысканиях, строительстве и эксплуатации зданий и сооружений, межевании земель, ведении кадастров и осуществлении иных специальных работ. Обязательным требованием при установлении местных систем координат является обеспечение возможности перехода от местной системы координат к государственной системе координат, который осуществляется с использованием параметров перехода (ключей). Каждая местная система координат может создаваться с одной или несколькими трех или шести градусными зонами. Параметры местных систем координат и ключи перехода к государственной системе координат (формулы и правила, по которым координаты точек в одной системе можно получить в другой системы) устанавливает Росреестр по согласованию с Минобороны РФ.
Определение положения точек в различных СК
Положение точек непосредственно на физической поверхности Земли или в околоземном пространстве, а также на поверхности земного эллипсоида могут определяться в различных как прямолинейных, так и криволинейных системах координат. Однако в теории и практике производства топографо-геодезических работ наибольшее распространение получили следующие СК:
Пространственные прямоугольные декартовы СК – Х, У, Z;
Отличительной особенностью использования в геодезии системы пространственных полярных геодезических координат является то, что ее основная плоскость выбирается на поверхности и представляет собой плоскость геодезического горизонта (или параллельная плоскости горизонта). За полярную ось принимается линия пересечения плоскости горизонта с плоскостью геодезического меридиана данной точки О (полюса системы) с положительным направлением на северный полюс Земли. Положение точки Q в этой СК определяется тремя величинами (координатами): S – длина прямой OQ; А – геодезический азимут (двугранный угол между плоскостью геодезического меридиана начальной точки О и нормальной плоскостью точки О, содержащей точку Q); Zг – зенитное расстояние (угол между нормалью точки О и линией OQ).
Криволинейные эллипсоидальные геодезические координаты – B, L, H;
Также очень широкое распространение имеют криволинейные эллипсоидальные системы геодезических координат. Эти СК непосредственно связаны с некоторой математической моделью земной поверхности, в качестве которой в настоящее время принимается поверхность эллипсоида вращения с определенными параметрами и ориентировкой его в теле Земли, и обычно называется он просто – земным эллипсоидом. Таким образом, земным эллипсоидом является эллипсоид вращения, форма и размеры которого с той или иной степенью точности соответствуют форме и размерам Земли. Для определения формы и размеров земного эллипсоида достаточно задать его основные параметры а – большую и b – малую полуоси. Однако на практике обычно для этих целей используются два других его элемента – одна линейная величина, например, большая полуось и одна относительная. В качестве относительной величины чаще всего используется его сжатие α, вычисляемое по формуле:
Если земной эллипсоид наилучшим образом представляет собой всю землю в целом, то такой эллипсоид называется общим земным эллипсоидом, и определяться он должен с соблюдением следующих условий:
1. Совпадение центра эллипсоида с центром масс Земли и плоскости его экватора с плоскостью земного экватора;
2. Минимум суммы квадратов уклонений по высоте квазигеоида (геоида), во всех его точках, от поверхности эллипсоида.
Различные виды систем полярных координат как пространственных, так и на поверхностях (сферы, эллипсоида, плоскости);
Название Местных Систем Координат по регионам
МСК-01 Республика Адыгея
МСК-02 Республика Башкортостан
МСК-03 Республика Бурятия
МСК-04 Республика Алтай
МСК-05 Республика Дагестан
МСК-06 Республика Ингушетия
МСК-07 Кабардино-Балкарская Республика
МСК-08 Республика Калмыкия
МСК-09 Республика Карачаево-Черкесия
МСК-10 Республика Карелия
МСК-11 Республика Коми
МСК-12 Республика Марий Эл
МСК-13 Республика Мордовия
МСК-14 Республика Саха (Якутия)
МСК-15 Северная Осетия — Алания
МСК-16 Республика Татарстан
МСК-18 Удмуртская Республика
МСК-20 Чеченская Республика
МСК-21 Чувашская Республика
МСК-22 Алтайский край
МСК-23 Краснодарский край
МСК-24 Красноярский край
МСК-25 Приморский край
МСК-26 Ставропольский край
МСК-27 Хабаровский край
МСК-28 Амурская область
МСК-29 Архангельская область
МСК-30 Астраханская область
МСК-31 Белгородская область
МСК-32 Брянская область
МСК-33 Владимирская область
МСК-34 Волгоградская область
МСК-35 Вологодская область
МСК-36 Воронежская область
МСК-37 Ивановская область
МСК-38 Иркутская область
МСК-39 Калининградская область
МСК-40 Калужская область
МСК-41 Камчатский край
МСК-42 Кемеровская область
МСК-43 Кировская область
МСК-44 Костромская область
МСК-45 Курганская область
МСК-46 Курская область
МСК-47 Ленинградская область
МСК-1964 город Санкт-Петербург
МСК-48 Липецкая область
МСК-49 Магаданская область
МСК-50 Московская область
МГГТ Москва
МСК-51 Мурманская область
МСК-52 Нижегородская область
МСК-53 Новгородская область
МСК-54 Новосибирская область
МСК-55 Омская область
МСК-56 Оренбургская область
МСК-57 Орловская область
МСК-58 Пензенская область
МСК-59 Пермский край
МСК-60 Псковская область
МСК-61 Ростовская область
МСК-62 Рязанская область
МСК-63 Самарская область
МСК-64 Саратовская область
МСК-65 Сахалинская область
МСК-66 Свердловская область
МСК-67 Смоленская область
МСК-68 Тамбовская область
МСК-69 Тверская область
МСК-70 Томская область
МСК-71 Тульская область
МСК-72 Тюменская область
МСК-73 Ульяновская область
МСК-74 Челябинская область
МСК-75 Забайкальский край
МСК-76 Ярославская область
МСК-83 Ненецкий автономный округ
МСК-86 Ханты-Мансийский автономный округ — Югра
МСК-87 Чукотский автономный округ
Система координат
Из Википедии — свободной энциклопедии
Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.
В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.
В астрономии небесные координаты — упорядоченная пара угловых величин (например, прямое восхождение и склонение), с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой сферическую систему координат (без радиальной координаты) с соответствующим образом выбранной фундаментальной плоскостью и началом отсчёта. В зависимости от выбора фундаментальной плоскости система небесных координат называется горизонтальной (плоскость горизонта), экваториальной (плоскость экватора), эклиптической (плоскость эклиптики) или галактической (галактическая плоскость).
Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.
В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.
В географии координаты выбираются как (приближённо) сферическая система координат — широта, долгота и высота над известным общим уровнем (например, океана).
В астрономии небесные координаты — упорядоченная пара угловых величин (например, прямое восхождение и склонение), с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой сферическую систему координат (без радиальной координаты) с соответствующим образом выбранной фундаментальной плоскостью и началом отсчёта. В зависимости от выбора фундаментальной плоскости система небесных координат называется горизонтальной (плоскость горизонта), экваториальной (плоскость экватора), эклиптической (плоскость эклиптики) или галактической (галактическая плоскость).
Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.
В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.
В географии координаты выбираются как (приближённо) сферическая система координат — широта, долгота и высота над известным общим уровнем (например, океана).
В астрономии небесные координаты — упорядоченная пара угловых величин (например, прямое восхождение и склонение), с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой сферическую систему координат (без радиальной координаты) с соответствующим образом выбранной фундаментальной плоскостью и началом отсчёта. В зависимости от выбора фундаментальной плоскости система небесных координат называется горизонтальной (плоскость горизонта), экваториальной (плоскость экватора), эклиптической (плоскость эклиптики) или галактической (галактическая плоскость).
Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.