Для чего нужна сортировка
Зачем нужна сортировка в программировании
И почему это любят спрашивать на собеседовании.
Приходишь такой на собеседование, а тебе говорят: «Расскажи про алгоритмы сортировок?» А зачем? А нельзя просто отсортировать и всё?
Что такое сортировка
Сортировка данных — это когда мы их упорядочиваем по какому-то признаку.
Например, в школе есть классный журнал, в котором все ученики отсортированы по фамилии. Или товары в интернет-магазине могут выводиться сначала дешёвые, потом дорогие. Или бывает сортировка товаров по популярности: используют внутреннюю переменную «популярность товара» и смотрят на её значение.
Почему нельзя просто отсортировать
Если у вас небольшой и понятный массив, то ничто не мешает взять встроенную функцию языка программирования типа sort() в JavaScript. Она пошуршит каким-то своим алгоритмом и вернёт отсортированный массив.
Сложности с сортировкой начинаются, когда:
❌ массивы данных большие — на тысячи, десятки и сотни тысяч элементов;
❌ может быть затруднён доступ к данным (например, они идут потоком);
❌ возможностей железа не хватает и нужны более экономные алгоритмы, чем те, которые встроены в язык программирования.
Тогда нужно выбирать специализированные алгоритмы сортировки, а то и оптимизировать их под свои задачи.
Какие бывают сортировки
Существуют десятки алгоритмов сортировки, каждый из которых хорош в чём-то своём. На одних легко объяснять принципы сортировки, другие хороши при работе с большими массивами, третьи оптимизированы по скорости, четвёртые — по числу процессорных циклов, компактности кода и т. д.
Самые популярные, которые вы встретите:
В ближайших статьях покажем примеры.
Почему про это любят спрашивать на собеседованиях
На собеседовании вам могут предложить либо выбрать сортировочный алгоритм под задачу, либо реализовать его для конкретных данных. Зачем это:
В целом ничто не мешает натренироваться в вопросах сортировки и показать через это свою эрудированность.
Что дальше
Впереди много разных видов сортировок — как работают, чем отличаются, где применяются. А главное — мы наглядно покажем, что делают популярные сортировки и почему их назвали именно так.
Для чего нужна сортировка
Под сортировкой понимают процесс размещения элементов заданного множества объектов в некотором определенном порядке.
На алгоритмах сортировки наглядно демонстрируется насколько разными путями можно прийти к одной цели – получению упорядоченного массива.
При множестве алгоритмов сортировки становится понятной необходимость их сравнительного анализа и оценки качества, критериями которого являются быстродействие и экономия памяти.
Зачем нужна сортировка? Когда элементы отсортированы, их проще найти, производить с ними различные операции. Легче определить пропущенные элементы. Легче найти общие элементы двух массивов. Сортировка влияет на скорость алгоритма, в котором нужно обратиться к определённому элементу массива.
1. Сортировка обменом (метод пузырька).
Суть метода. Все соседние элементы массива попарно сравниваются друг с другом и меняются местами в том случае, если предшествующий элемент больше последующего. В результате этого максимальный элемент постепенно смещается вправо и в конце концов занимает крайнее правое место в массиве, после чего исключается из дальнейшей обработки. Затем процесс повторяется, и сове место занимает второй по величине элемент, который также исключается из дальнейшего рассмотрения. Так до тех пор, пока вся последовательность не будет упорядочена.
Недостаток. Если на каком-то шаге проверки получена упорядоченная последовательность, то просмотры массива все равно продолжаются.
Как улучшить. Можно включить условие проверки – если на очередном проходе не сделано ни одного обмена, то массив стал упорядоченным, и его сортировку можно прекратить.
Модификация пузырькового метода. Шейкер-сортировка. Сортировка проходит в массиве в обоих направлениях, а не только от его начала к концу.
В работе с большими массивами преимущество шейкер-сортировки уменьшается за счёт использования двух циклов.
2. Сортировка выбором.
Суть метода. В упорядоченной последовательности выбирается минимальный элемент. Этот элемент меняется местами с первым элементом и исключается из дальнейшей обработки, а оставшаяся последовательность принимается за исходную. Процесс повторяется до тех пор, пока все элементы не будут выбраны, а полученный массив не станет упорядоченным.
3. Сортировка методом прямого включения (простыми вставками).
4. Обменная сортировка с разделением (быстрая сортировка Хоара).
Суть метода. В исходном неотсортированном массиве выбрать некоторый элемент х=а[ k ] (барьерный элемент). Переставить элементы массива таким образом, чтобы слева от х оказались элементы, меньшие или равные х, а справа – элементы, большие х. разделив таким образом массив, можно сделать то же самое с обеими полученными частями, а затем – с частями этих частей и т.д., пока каждая часть будет содержать только один элемент.
Метод бинарного поиска элементов в массиве.
Часто требуется провести поиск элемента в упорядоченном массиве. Например, массив фамилий упорядочен по алфавиту, массив результатов соревнований по прыжкам в длину упорядочен по убыванию.
Для поиска в упорядоченных массивах можно применить достаточно эффективный метод – метод бинарного поиска.
Суть метода. Исходный массив делится пополам и для сравнения выбирается средний элемент. Если он совпадает с искомым, то поиск заканчивается. Если же средний элемент меньше искомого, то все элементы левее его также будут меньше искомого. следовательно, их можно исключить из дальнейшего поиска, оставив только правую часть массива. Аналогично, если средний элемент больше искомого, то отбрасывается правая часть, а остается левая.
Итак далее, пока элемент не будет найден или длина зоны поиска станет равной нулю. В последнем случае искомый элемент найден не будет.
О сортировках (пузырьковой, быстрой, расческой. )
Эта статья ориентирована в первую очередь на начинающих программистов. О сортировках вообще и об упомянутых в заголовке в интернете море статей, зачем нужно еще одна? Например, есть хорошая статья здесь, на хабре: Пузырьковая сортировка и все-все-все. Во-первых, хорошего много не бывает, во-вторых в этой статье я хочу ответь на вопросы «зачем, что, как, почему».Зачем нужны сортировки? В первую очередь, для поиска и представления данных. Некоторые задачи с неотсортированными данными решить очень трудно, а некоторые просто невозможно. Пример: орфографический словарь, в нем слова отсортированы по алфавиту. Если бы это было не так, то попробуйте найти в нем нужное слово. Телефонная книга, где абоненты отсортированы по алфавиту. Даже если сортировка не обязательна и не сильно нужна, все равно бывает удобнее работать с отсортированными данными.
Время сортировки 100001 элемента
Измерим время сортировки для массива, содержащего 100001 элемент на компьютере с процессором Intel i5 (3.3Ггц).Время указано в сек, через дробь указано количество проходов (для быстрой сортировки оно неизвестно).Как и ожидалось, шейкерная сортировка на проблемном массиве (который полностью упорядочен, только первый и последний элементы переставлены) абсолютный лидер. Она идеально «заточена» под эти данные. Но на случайных данных сортировки расческой и qsort не оставляют соперницам шанса. Пузырьковая сортировка на проблемном массиве показывает двукратное увеличение скорости по сравнению с случайным просто потому, что количество операций перестановки на порядки меньше.
| Сортировка | Простая | Пузырьковая | Шейкерная | Расчёской | Быстрая (qsort) |
|---|---|---|---|---|---|
| Стабильная | + | + | + | — | — |
| Случайный | 23.1/100000 | 29.1/99585 | 19.8/50074 | 0.020/49 | 0.055 |
| Проблемный | 11.5/100000 | 12.9/100000 | 0.002/3 | 0.015/48 | 0.035 |
| Обратный | 18.3/100000 | 21.1/100000 | 21.1/100001 | 0.026/48 | 0.037 |
А теперь вернемся к истокам, к пузырьковой сортировке и воочию посмотрим на процесс сортировки. Видите, как на первом проходе тяжелый элемент (50) переносится в конец?

Сравниваемые элементы показаны в зеленых рамках, а переставленные — в красных
Дополнение после публикации
Я ни коей мере не считаю qsort плохой или медленной — она достаточно быстра, функциональна и при возможности следует пользоваться именно ею. Да, ей приходится тратить время на вызов функции сравнения и она уступила «расческе», которая сравнивает «по месту». Это отставание несущественно (сравните с отставанием пузырька от qsort, которое будет увеличиваться при росте массива). Пусть теперь надо сравнивать не числа, а какую-то сложную структуру по определенному полю и пусть эта структура состоит из 1000 байтов. Поместим 100тыс элементов в массив (100мб — это кое-что) и вызовем qsort. Функция fcomp (функция-компаратор) сравнит нужные поля и в результате получится отсортированный массив. При этом при перестановке элементов qsort придется 3 раза копировать фрагменты по 1000 байтов. А теперь «маленькая хитрость» — создадим массив из 100тыс ссылок на исходные элементы и передадим в qsort начало этого массива ссылок. Поскольку ссылка занимает 4 байта (в 64 битных 8), а не 1000, то при обмене ссылок qsort надо поменять эти 4/8 байтов. Разумеется, нужно будет изменить fcomp, поскольку в качестве параметров она теперь получит не адреса элементов, а адреса адресов элементов (но это несложное изменение). Зато теперь можно сделать несколько функций сортировки (каждая сортирует по своему полю структуры). И даже, при необходимости, можно сделать несколько массивов ссылок. Вот сколько возможностей дает qsort!
Кстати: использование ссылок на объекты вместо самих объектов может быть полезно не только при вызове qsort, но и при применении таких контейнеров как vector, set или map.
Алгоритмы и структуры данных для начинающих: сортировка
В этой части мы посмотрим на пять основных алгоритмов сортировки данных в массиве. Начнем с самого простого — сортировки пузырьком — и закончим «быстрой сортировкой» (quicksort).
Для каждого алгоритма, кроме объяснения его работы, мы также укажем его сложность по памяти и времени в наихудшем, наилучшем и среднем случае.
Метод Swap
Пузырьковая сортировка
| Сложность | Наилучший случай | В среднем | Наихудший случай |
| Время | O(n) | O(n 2 ) | O(n 2 ) |
| Память | O(1) | O(1) | O(1) |
Сортировка пузырьком — это самый простой алгоритм сортировки. Он проходит по массиву несколько раз, на каждом этапе перемещая самое большое значение из неотсортированных в конец массива.
27–29 декабря, Онлайн, Беcплатно
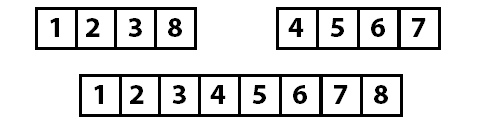
Например, у нас есть массив целых чисел:
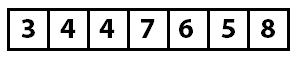
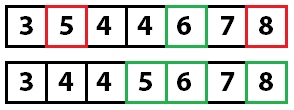
При первом проходе по массиву мы сравниваем значения 3 и 7. Поскольку 7 больше 3, мы оставляем их как есть. После чего сравниваем 7 и 4. 4 меньше 7, поэтому мы меняем их местами, перемещая семерку на одну позицию ближе к концу массива. Теперь он выглядит так:
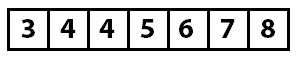
Этот процесс повторяется до тех пор, пока семерка не дойдет почти до конца массива. В конце она сравнивается с элементом 8, которое больше, а значит, обмена не происходит. После того, как мы обошли массив один раз, он выглядит так:
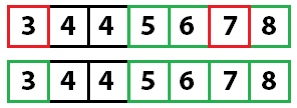
Поскольку был совершен по крайней мере один обмен значений, нам нужно пройти по массиву еще раз. В результате этого прохода мы перемещаем на место число 6.
И снова был произведен как минимум один обмен, а значит, проходим по массиву еще раз.
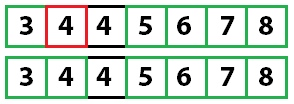
При следующем проходе обмена не производится, что означает, что наш массив отсортирован, и алгоритм закончил свою работу.
Сортировка вставками
| Сложность | Наилучший случай | В среднем | Наихудший случай |
| Время | O(n) | O(n 2 ) | O(n 2 ) |
| Память | O(1) | O(1) | O(1) |
Сортировка вставками работает, проходя по массиву и перемещая нужное значение в начало массива. После того, как обработана очередная позиция, мы знаем, что все позиции до нее отсортированы, а после нее — нет.
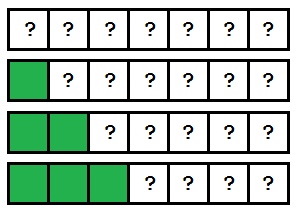
Важный момент: сортировка вставками обрабатывает элементы массива по порядку. Поскольку алгоритм проходит по элементам слева направо, мы знаем, что все, что слева от текущего индекса — уже отсортировано. На этом рисунке показано, как увеличивается отсортированная часть массива с каждым проходом:
Постепенно отсортированная часть массива растет, и, в конце концов, массив окажется упорядоченным.
Давайте взглянем на конкретный пример. Вот наш неотсортированный массив, который мы будем использовать:
Алгоритм начинает работу с индекса 0 и значения 3. Поскольку это первый индекс, массив до него включительно считается отсортированным.
Далее мы переходим к числу 7. Поскольку 7 больше, чем любое значение в отсортированной части, мы переходим к следующему элементу.
На этом этапе элементы с индексами 0..1 отсортированы, а про элементы с индексами 2..n ничего не известно.
Итак, мы нашли индекс 1 (между значениями 3 и 7). Метод Insert осуществляет вставку, удаляя вставляемое значение из массива и сдвигая все значения, начиная с индекса для вставки, вправо. Теперь массив выглядит так:
Теперь часть массива, начиная от нулевого элемента и заканчивая элементом с индексом 2, отсортирована. Следующий проход начинается с индекса 3 и значения 4. По мере работы алгоритма мы продолжаем делать такие вставки.
Когда больше нет возможностей для вставок, массив считается полностью отсортированным, и работа алгоритма закончена.
Сортировка выбором
| Сложность | Наилучший случай | В среднем | Наихудший случай |
| Время | O(n) | O(n 2 ) | O(n 2 ) |
| Память | O(1) | O(1) | O(1) |
Сортировка выбором — это некий гибрид между пузырьковой и сортировкой вставками. Как и сортировка пузырьком, этот алгоритм проходит по массиву раз за разом, перемещая одно значение на правильную позицию. Однако, в отличие от пузырьковой сортировки, он выбирает наименьшее неотсортированное значение вместо наибольшего. Как и при сортировке вставками, упорядоченная часть массива расположена в начале, в то время как в пузырьковой сортировке она находится в конце.
Давайте посмотрим на работу сортировки выбором на нашем неотсортированном массиве.
При первом проходе алгоритм с помощью метода FindIndexOfSmallestFromIndex пытается найти наименьшее значение в массиве и переместить его в начало.
Имея такой маленький массив, мы сразу можем сказать, что наименьшее значение — 3, и оно уже находится на правильной позиции. На этом этапе мы знаем, что на первой позиции в массиве (индекс 0) находится самое маленькое значение, следовательно, начало массива уже отсортировано. Поэтому мы начинаем второй проход — на этот раз по индексам от 1 до n — 1.
На втором проходе мы определяем, что наименьшее значение — 4. Мы меняем его местами со вторым элементом, семеркой, после чего 4 встает на свою правильную позицию.
Теперь неотсортированная часть массива начинается с индекса 2. Она растет на один элемент при каждом проходе алгоритма. Если на каком-либо проходе мы не сделали ни одного обмена, это означает, что массив отсортирован.
После еще двух проходов алгоритм завершает свою работу:
Сортировка слиянием
| Сложность | Наилучший случай | В среднем | Наихудший случай |
| Время | O(n·log n) | O(n·log n) | O(n·log n) |
| Память | O(n) | O(n) | O(n) |
Разделяй и властвуй
До сих пор мы рассматривали линейные алгоритмы. Они используют мало дополнительной памяти, но имеют квадратичную сложность. На примере сортировки слиянием мы посмотрим на алгоритм типа «разделяй и властвуй» (divide and conquer).
Алгоритмы этого типа работают, разделяя крупную задачу на более мелкие, решаемые проще. Мы пользуемся ими каждый день. К примеру, поиск в телефонной книге — один из примеров такого алгоритма.
Если вы хотите найти человека по фамилии Петров, вы не станете искать, начиная с буквы А и переворачивая по одной странице. Вы, скорее всего, откроете книгу где-то посередине. Если попадете на букву Т, перелистнете несколько страниц назад, возможно, слишком много — до буквы О. Тогда вы пойдете вперед. Таким образом, перелистывая туда и обратно все меньшее количество страниц, вы, в конце концов, найдете нужную.
Насколько эффективны эти алгоритмы?
Предположим, что в телефонной книге 1000 страниц. Если вы открываете ее на середине, вы отбрасываете 500 страниц, в которых нет искомого человека. Если вы не попали на нужную страницу, вы выбираете правую или левую сторону и снова оставляете половину доступных вариантов. Теперь вам надо просмотреть 250 страниц. Таким образом мы делим нашу задачу пополам снова и снова и можем найти человека в телефонной книге всего за 10 просмотров. Это составляет 1% от всего количества страниц, которые нам пришлось бы просмотреть при линейном поиске.
Сортировка слиянием
При сортировке слиянием мы разделяем массив пополам до тех пор, пока каждый участок не станет длиной в один элемент. Затем эти участки возвращаются на место (сливаются) в правильном порядке.
Давайте посмотрим на такой массив:
Разделим его пополам:
И будем делить каждую часть пополам, пока не останутся части с одним элементом:
Теперь, когда мы разделили массив на максимально короткие участки, мы сливаем их в правильном порядке.
Сначала мы получаем группы по два отсортированных элемента, потом «собираем» их в группы по четыре элемента и в конце собираем все вместе в отсортированный массив.
Для работы алгоритма мы должны реализовать следующие операции:
Стоит отметить, что в отличие от линейных алгоритмов сортировки, сортировка слиянием будет делить и склеивать массив вне зависимости от того, был он отсортирован изначально или нет. Поэтому, несмотря на то, что в худшем случае он отработает быстрее, чем линейный, в лучшем случае его производительность будет ниже, чем у линейного. Поэтому сортировка слиянием — не самое лучшее решение, когда надо отсортировать частично упорядоченный массив.
Быстрая сортировка
| Сложность | Наилучший случай | В среднем | Наихудший случай |
| Время | O(n·log n) | O(n·log n) | O(n 2 ) |
| Память | O(1) | O(1) | O(1) |
Быстрая сортировка — это еще один алгоритм типа «разделяй и властвуй». Он работает, рекурсивно повторяя следующие шаги:
Давайте посмотрим на работу алгоритма на следующем массиве:
Сначала мы случайным образом выбираем ключевой элемент:
Теперь, когда мы знаем ключевой индекс (4), мы берем значение, находящееся по этому индексу (6), и переносим значения в массиве так, чтобы все числа больше или равные ключевому были в правой части, а все числа меньше ключевого — в левой. Обратите внимание, что в процессе переноса значений индекс ключевого элемента может измениться (мы увидим это вскоре).
На этом этапе мы знаем, что значение 6 находится на правильной позиции. Теперь мы повторяем этот процесс для правой и левой частей массива.
Мы рекурсивно вызываем метод quicksort на каждой из частей. Ключевым элементом в левой части становится пятерка. При перемещении значений она изменит свой индекс. Главное — помнить, что нам важно именно ключевое значение, а не его индекс.
Снова применяем быструю сортировку:
У нас осталось одно неотсортированное значение, а, поскольку мы знаем, что все остальное уже отсортировано, алгоритм завершает работу.
Заключение
На этом мы заканчиваем наш цикл статей по алгоритмам и структурам данных для начинающих. За это время мы рассмотрели связные списки, динамические массивы, двоичное дерево поиска и множества с примерами кода на C#.
Основные виды сортировок и примеры их реализации
Памятка для тех, кто готовится к собеседованию на позицию разработчика
На собеседованиях будущим стажёрам-разработчикам дают задания на знание структур данных и алгоритмов — в том числе сортировок. Академия Яндекса и соавтор специализации «Искусство разработки на современном C++» Илья Шишков составили список для подготовки с методами сортировки, примерами их реализации и гифками, чтобы лучше понять, как они работают.
Пузырьковая сортировка и её улучшения
Сортировка пузырьком
Сортировка пузырьком — один из самых известных алгоритмов сортировки. Здесь нужно последовательно сравнивать значения соседних элементов и менять числа местами, если предыдущее оказывается больше последующего. Таким образом элементы с большими значениями оказываются в конце списка, а с меньшими остаются в начале.
Этот алгоритм считается учебным и почти не применяется на практике из-за низкой эффективности: он медленно работает на тестах, в которых маленькие элементы (их называют «черепахами») стоят в конце массива. Однако на нём основаны многие другие методы, например, шейкерная сортировка и сортировка расчёской.
Сортировка перемешиванием (шейкерная сортировка)
Шейкерная сортировка отличается от пузырьковой тем, что она двунаправленная: алгоритм перемещается не строго слева направо, а сначала слева направо, затем справа налево.
Сортировка расчёской
Сортировка расчёской — улучшение сортировки пузырьком. Её идея состоит в том, чтобы «устранить» элементы с небольшими значения в конце массива, которые замедляют работу алгоритма. Если при пузырьковой и шейкерной сортировках при переборе массива сравниваются соседние элементы, то при «расчёсывании» сначала берётся достаточно большое расстояние между сравниваемыми значениями, а потом оно сужается вплоть до минимального.
Первоначальный разрыв нужно выбирать не случайным образом, а с учётом специальной величины — фактора уменьшения, оптимальное значение которого равно 1,247. Сначала расстояние между элементами будет равняться размеру массива, поделённому на 1,247; на каждом последующем шаге расстояние будет снова делиться на фактор уменьшения — и так до окончания работы алгоритма.
Простые сортировки
Сортировка вставками
При сортировке вставками массив постепенно перебирается слева направо. При этом каждый последующий элемент размещается так, чтобы он оказался между ближайшими элементами с минимальным и максимальным значением.
Сортировка выбором
Сначала нужно рассмотреть подмножество массива и найти в нём максимум (или минимум). Затем выбранное значение меняют местами со значением первого неотсортированного элемента. Этот шаг нужно повторять до тех пор, пока в массиве не закончатся неотсортированные подмассивы.
Быстрая сортировка
Этот алгоритм состоит из трёх шагов. Сначала из массива нужно выбрать один элемент — его обычно называют опорным. Затем другие элементы в массиве перераспределяют так, чтобы элементы меньше опорного оказались до него, а большие или равные — после. А дальше рекурсивно применяют первые два шага к подмассивам справа и слева от опорного значения.
Быструю сортировку изобрели в 1960 году для машинного перевода: тогда словари хранились на магнитных лентах, а сортировка слов обрабатываемого текста позволяла получить переводы за один прогон ленты, без перемотки назад.
Сортировка слиянием
Сортировка слиянием пригодится для таких структур данных, в которых доступ к элементам осуществляется последовательно (например, для потоков). Здесь массив разбивается на две примерно равные части и каждая из них сортируется по отдельности. Затем два отсортированных подмассива сливаются в один.
Пирамидальная сортировка
При этой сортировке сначала строится пирамида из элементов исходного массива. Пирамида (или двоичная куча) — это способ представления элементов, при котором от каждого узла может отходить не больше двух ответвлений. А значение в родительском узле должно быть больше значений в его двух дочерних узлах.
Пирамидальная сортировка похожа на сортировку выбором, где мы сначала ищем максимальный элемент, а затем помещаем его в конец. Дальше нужно рекурсивно повторять ту же операцию для оставшихся элементов.