Для чего нужна теорема коши

КОШИ ТЕОРЕМА

— 1) К. т. о многогранниках: два замкнутых выпуклых многогранника конгруэнтны, если между их истинными гранями, ребрами и вершинами имеется сохраняющее инцидентность взаимно однозначное соответствие, причем соответствующие грани многогранников конгруэнтны. К. т.- первая теорема об однозначной определенности выпуклых поверхностей, поскольку многогранники, о к-рых идет речь в К. т., изометричны в смысле внутренней метрики. К. т. является частным случаем теоремы о том, что всякая замкнутая выпуклая поверхность однозначно определяется своей метрикой (см. [4]).

К. т. установлена О. Коши (см. [1]).

Лит.:[1]Cauchy A. L., «J. Ecole polytechn.», 1813, t. 9, p. 87-98; [2] А л е к с а н д р о в А. Д., Выпуклые многогранники, М.- Л., 1950; [3] А дам ар Ж., Элементарная геометрия, 3 изд., ч. 2, М., 1958; [4] Погорелов А. В., Однозначная определенность выпуклых поверхностей, М.- Л., 1949 (Тр. Матем. ин-та АН СССР, т. 29). Е. В. Шикин.

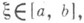
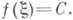
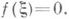
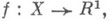
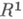
2) К. т. о промежуточных значениях непрерывной функции на отрезке: если функция f, значениями к-рой являются действительные числа, непрерывна на [a, b]и число Слежит между f(a) и f(b), то существует такая точка что В частности, если f(a) и f(b).имеют разные знаки, то существует такая точка , что В этой форме К. т. используют для выделения промежутков, в к-рых заведомо имеются нули рассматриваемой функции. Из К. т. следует, что образом промежутка числовой прямой при его непрерывном отображении в числовую прямую является также промежуток. К. т. допускает обобщение на топология, пространства: всякая непрерывная функция определенная на связном топологич. пространстве X( — множество действительных чисел), принимающая какие-либо два значения, принимает и любое лежащее между ними, поэтому образ пространства Xтакже промежуток числовой прямой.

К. т. была сформулирована независимо Б. Больцано (В. Bolzano, 1817) и О. Коши (A. Cauchy, 1821).

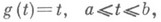
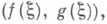
При получается формула конечных приращений Лагранжа. Геометрич. смысл К. т. состоит в том, что на всякой непрерывной кривой x=f(t), y=g(t). лежащей на плоскости хОу и имеющей в каждой точке (f(t). g(t)).касательную, есть точка в к-рой касательная параллельна хорде, соединяющей концы (f(a), g(a)) и(f(b), g(b)).рассматриваемой кривой.

Лит.:[1] Ильин В. А., П о з н я к Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971; [2] Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1, М., 1973; [3] Н и к о л ь с к и и С. М., Курс математического анализа, 2 изд., т. 1, М., 1975. Л. Д. Кудрявцев.

4) К. т. в теории групп: если порядок конечной группы Gделится на простое число р, то Gобладает элементами порядка р.

Теорема была доказана О. Коши (см. [1]) для групп подстановок.

Лит.:[1] С а и с h у A. L., в кн.: Exercices d’analyse et de physique mathematique, t. 3, P., 1844, p. 151-252; [2] К у-p о ш А. Г., Теория групп, 3 изд., М., 1967.

Источник

КОШИ ТЕОРЕМА

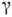
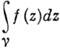
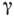
— теорема об обращении в нуль интеграла от аналитической функции, взятого вдоль замкнутого контура. Точнее, пусть ф-ция f(t) аналитична в области D, а — кусочно-гладкий контур, лежащий в D и не содержащий внутри себя особенностей ф-ции f(z). Тогда, согласно К. т., контурный интеграл равен нулю. Доказана О. Коши в 1825. Геометрически К. т. означает, что векторное поле, компонентами к-рого являются соответственно веществ. и мнимая части аналитич. ф-ции, потенциально и соленоидально, т. е. его дивергенция и ротор равны нулю. Справедливо и обратное утверждение (теорема Мореры): если ф-ция f(z) непрерывна в односвязной области D и такова, что для любого кусочно-гладкого замкнутого контура , лежащего в D, то f(z) аналитична в D. К. т. играет важную роль в теории аналитич. ф-ций. На ней основано представление аналитич. ф-ции в виде Коши интеграла, она используется в теории вычетов и т. д.

Полезное

Смотреть что такое «КОШИ ТЕОРЕМА» в других словарях:

Коши теорема — Теоремой Коши называются следующие утверждения: Интегральная теорема Коши Теорема Коши о многогранниках Теорема Коши о среднем значении Теорема Коши (теория групп) См. также Признак Коши Теорема Больцано Коши Условия Коши Римана … Википедия

КОШИ ТЕОРЕМА — 1) К. т. о многогранниках: два замкнутых выпуклых многогранника конгруэнтны, если между их истинными гранями, ребрами и вершинами имеется сохраняющее инцидентность взаимно однозначное соответствие, причем соответствующие грани многогранников… … Математическая энциклопедия

Коши теорема — о разложении аналитической функции (См. Аналитические функции) в степенной ряд. Пусть f (z) функция, однозначная и аналитическая в области G; z0 произвольная (конечная) точка области G и ρ расстояние от z0 до границы этой области. Тогда… … Большая советская энциклопедия

Коши Огюстен Луи — Коши (Cauchy) Огюстен Луи (21.8.1789, Париж, ≈ 23.5.1857, Со), французский математик, член Парижской АН (1816). Окончил Политехническую школу (1807) и Школу мостов и дорог (1810) в Париже. В 1810≈13 работал инженером в г. Шербур. В 1816≈30… … Большая советская энциклопедия

Коши, Огюстен — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши О. — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши О. Л. — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши Огюстен Луи — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши барон — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши, Огюстен Луи — Огюстен Луи Коши Augustin Louis Cauchy … Википедия

Источник

Коши теорема

Смотреть что такое «Коши теорема» в других словарях:

КОШИ ТЕОРЕМА — теорема об обращении в нуль интеграла от аналитической функции, взятого вдоль замкнутого контура. Точнее, пусть ф ция f(t) аналитична в области D, а кусочно гладкий контур, лежащий в D и не содержащий внутри себя особенностей ф ции f(z). Тогда,… … Физическая энциклопедия

Коши теорема — Теоремой Коши называются следующие утверждения: Интегральная теорема Коши Теорема Коши о многогранниках Теорема Коши о среднем значении Теорема Коши (теория групп) См. также Признак Коши Теорема Больцано Коши Условия Коши Римана … Википедия

КОШИ ТЕОРЕМА — 1) К. т. о многогранниках: два замкнутых выпуклых многогранника конгруэнтны, если между их истинными гранями, ребрами и вершинами имеется сохраняющее инцидентность взаимно однозначное соответствие, причем соответствующие грани многогранников… … Математическая энциклопедия

Коши Огюстен Луи — Коши (Cauchy) Огюстен Луи (21.8.1789, Париж, ≈ 23.5.1857, Со), французский математик, член Парижской АН (1816). Окончил Политехническую школу (1807) и Школу мостов и дорог (1810) в Париже. В 1810≈13 работал инженером в г. Шербур. В 1816≈30… … Большая советская энциклопедия

Коши, Огюстен — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши О. — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши О. Л. — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши Огюстен Луи — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши барон — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши, Огюстен Луи — Огюстен Луи Коши Augustin Louis Cauchy … Википедия

Источник

Теорема Коши (теория групп)

Если порядок конечной группы делится на простое число , то обладает элементами порядка .

Является частным случаем теорем Силова.

История

Теорема была изначально доказана Коши для групп подстановок.

Литература

Полезное

Смотреть что такое «Теорема Коши (теория групп)» в других словарях:

Теорема Коши — Теоремой Коши называются следующие утверждения: Интегральная теорема Коши Теорема Коши о многогранниках Теорема Коши о среднем значении Теорема Коши (теория групп) См. также Признак Коши Теорема Больцано Коши Условия Коши Римана … Википедия

Теория групп — Группа (математика) Теория групп Осно … Википедия

Коши теорема — Теоремой Коши называются следующие утверждения: Интегральная теорема Коши Теорема Коши о многогранниках Теорема Коши о среднем значении Теорема Коши (теория групп) См. также Признак Коши Теорема Больцано Коши Условия Коши Римана … Википедия

Коши, Огюстен — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши О. — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши О. Л. — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши Огюстен Луи — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши барон — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия

Коши, Огюстен Луи — Огюстен Луи Коши Augustin Louis Cauchy … Википедия

КОШИ ТЕОРЕМА — 1) К. т. о многогранниках: два замкнутых выпуклых многогранника конгруэнтны, если между их истинными гранями, ребрами и вершинами имеется сохраняющее инцидентность взаимно однозначное соответствие, причем соответствующие грани многогранников… … Математическая энциклопедия

Источник