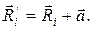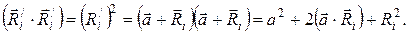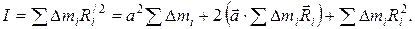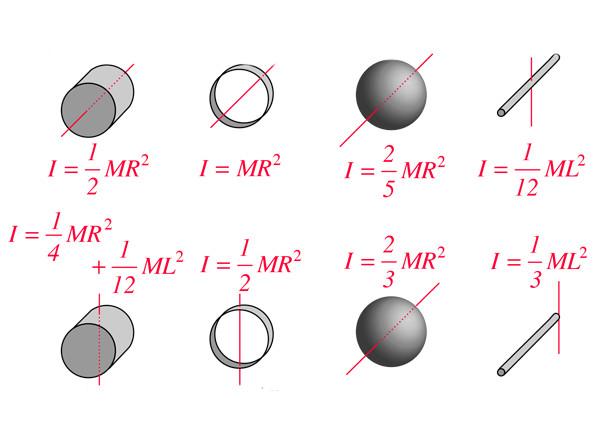Для чего нужна теорема штейнера

Момент инерции для чайников: определение, формулы, примеры решения задач

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Источник

Теорема Штейнера или теорема параллельных осей для вычисления момента инерции

При математическом описании вращательного движения важно знать момент инерции системы относительно оси. В общем случае процедура нахождения этой величины предполагает реализацию процесса интегрирования. Облегчить вычисления позволяет так называемая теорема Штейнера. Рассмотрим ее подробнее в статье.

Что такое момент инерции?

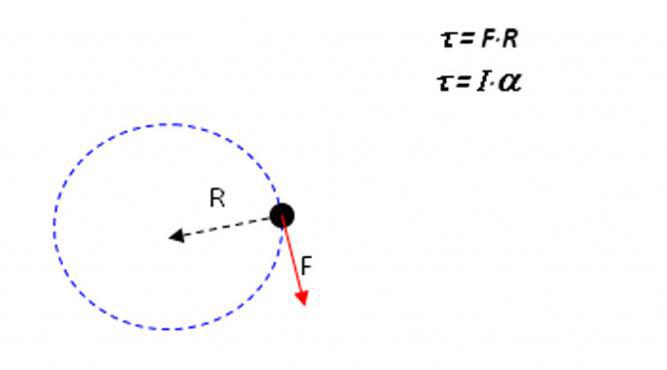
До того как привести формулировку теоремы Штейнера, следует разобраться с самим понятием момента инерции. Допустим, имеется некоторое тело определенной массы и произвольной формы. Этим телом может быть, как материальная точка, так и любой двумерный и трехмерный объект (стержень, цилиндр, шар и т.д.). Если рассматриваемый объект совершает круговое движение вокруг некоторой оси с постоянным угловым ускорением α, тогда можно записать следующее уравнение:

Вам будет интересно: Анализ занятия воспитателя детского сада: пример, схема

Момент инерции и теорема Штейнера

Известный швейцарский математик, Якоб Штейнер, доказал теорему о параллельных осях и моменте инерции, которая теперь носит его фамилию. Эта теорема постулирует, что момент инерции для абсолютно любого твердого тела произвольной геометрии относительно некоторой оси вращения равен сумме момента инерции относительно оси, которая пересекает центр масс тела и параллельна первой, и произведения массы тела на квадрат дистанции между этими осями. Математически эта формулировка записывается так:

Теорема позволяет, зная величину IO, рассчитать любой другой момент IZ относительно оси, которая параллельна O.

Доказательство теоремы

Формулу теоремы Штейнера можно легко получить самостоятельно. Для этого рассмотрим произвольное тело на плоскости xy. Пусть начало координат проходит через центр масс этого тела. Рассчитаем момент инерции IO которая проходит через начало координат перпендикулярно плоскости xy. Поскольку расстояние до любой точки тела выражается формулой r = √ (x2 + y2), тогда получаем интеграл:

IO = ∫m (r2*dm) = ∫m ( (x2+y2) *dm)

Теперь переместим параллельно ось вдоль оси x на расстояние l, например, в положительном направлении, тогда расчет для новой оси момента инерции будет выглядеть следующим образом:

Раскроем полный квадрат в скобках и разделим подынтегральные суммы, получим:

IZ = ∫m ( (x2+l2+2*x*l+y2)*dm) = ∫m ( (x2+y2)*dm) + 2*l*∫m (x*dm) + l2*∫mdm

Первое из этих слагаемых является величиной IO, третье слагаемое, после проведения интегрирования, дает член l2*m, а вот второе слагаемое равно нулю. Обнуление указанного интеграла связано с тем, что он берется от произведения иксов на элементы массы dm, что в среднем дает ноль, так как центр масс находится в начале координат. В итоге, получается формула теоремы Штейнера.

Рассмотренный случай на плоскости можно обобщить на объемное тело.

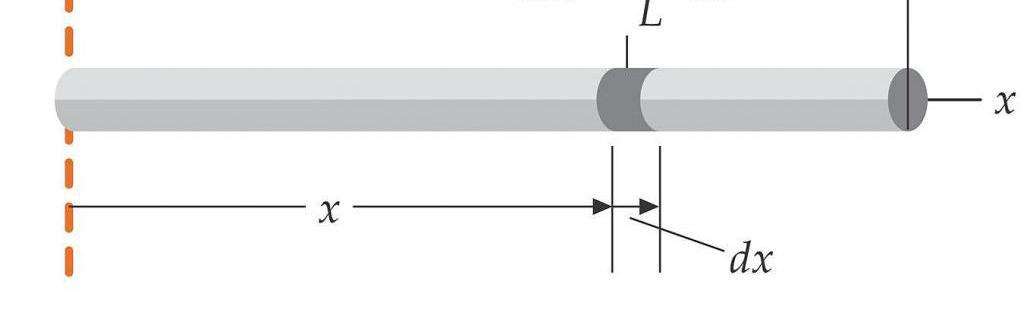
Проверка формулы Штейнера на примере стержня

Приведем простой пример, на котором продемонстрируем, как пользоваться рассмотренной теоремой.

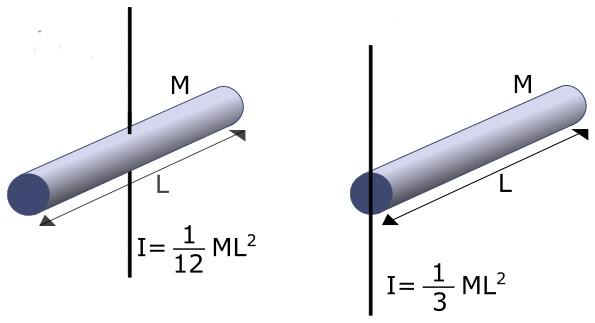
Известно, что для стержня длиной L и массой m момент инерции IO (ось проходит через центр масс) равен m*L2/12, а момент IZ (ось проходит через конец стержня) равен m*L2/3. Проверим эти данные, воспользовавшись теоремой Штейнера. Поскольку расстояние между двумя осями равно L/2, тогда получаем момент IZ:

IZ = IO + m*(L/2)2 = m*L2/12 + m*L2/4 = 4*m*L2/12 = m*L2/3

То есть мы проверили формулу Штейнера и получили такое же значение для IZ, что и в источнике.

Аналогичные вычисления можно проводить и для других тел (цилиндра, шара, диска), получая при этом необходимые моменты инерции, и не производя интегрирования.

Момент инерции и перпендикулярные оси

Рассмотренная теорема касается параллельных осей. Для полноты информации полезно также привести теорему для перпендикулярных осей. Она формулируется так: для плоского объекта произвольной формы момент инерции относительно перпендикулярной ему оси будет равен сумме двух моментов инерции относительно двух взаимно перпендикулярных и лежащих в плоскости объекта осей, при этом все три оси должны проходить через одну точку. Математически это записывается так:

Существенное отличие этой теоремы от теоремы Штейнера заключается в том, что она применима только к плоским (двумерным) твердым объектам. Тем не менее на практике ее достаточно широко используют, мысленно разрезая тело на отдельные слои, а затем, складывая полученные моменты инерции.

Источник

Теорема Штейнера

Предположим, что мы умеем вычислять моменты инерции относительно любой оси, проходящей через центр масс. Теперь возникает задача вычисления момента инерции тела относительно произвольной оси. Она решается с помощью теоремы Штейнера.

Эта теорема утверждает, что момент инерции тела относительно любой оси вращения равен моменту инерции относительно параллельной ей оси, проходящей через центр масс, сложенному с произведением массы тела на квадрат расстояния центра масс тела от оси вращения.

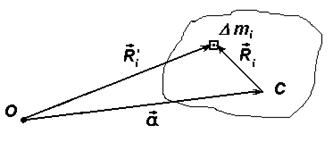
Для доказательства теоремы рассмотрим некую ось С, проходящую через центр масс и параллельную ей ось О, отстоящую от оси С на расстоянии а. Ось О может находиться и вне тела. Обе оси перпендикулярны плоскости чертежа (рис. 2.12).

Рис. 2.12. К доказательству теоремы Штейнера

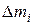
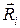
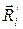
Из рис. 2.12 видно, что положение элемента массы относительно этих осей определяется векторами и , связь между которыми имеет вид:

Квадрат расстояния 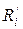равен скалярному произведению

Тогда момент инерции тела относительно оси О можно представить в следующем виде:

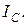
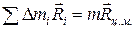
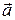
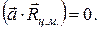
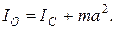
Последнее слагаемое в этом выражении есть момент инерции тела относительно оси, проходящей через центр масс. Обозначим его через Сумма . Напомним, что оси О и С параллельны и следовательно, вектор перпендикулярен оси С. Поэтому скалярное произведение Таким образом, мы получаем:

(2.10.1)

Уравнение движения твердого тела.

Абсолютно твердое тело имеет шесть степеней свободы и, следовательно, его движение описывается с помощью шести дифференциальных уравнений второго порядка. Три из них описывают движение центра масс твердого тела:

, , , (2.11.1)

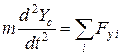
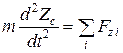
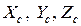
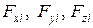
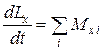
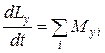
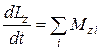
где — координаты центра масс тела, — проекции внешних сил на оси координат, m — масса тела. Три других являются уравнениями моментов относительно осей ОХ, ОУ и ОZ в декартовой системе координат:

, , , (2.11.2)

Если перемещать точку приложения силы вдоль линии ее действия, то моменты сил и результирующие силы не будут меняться, если мы имеем дело с абсолютно твердым телом. В этом случае не будут меняться и уравнения движения (2.11.1), (2.11.2).

Если найдены решения уравнений (2.11.1), (2.11.2), при известных начальных условиях, то определены и шесть координат, характеризующих движение твердого тела. Эти координаты являются функциями времени. Однако системы уравнений (2.11.1) и (2.11.2) не всегда позволяют получить решение в аналитической форме. В этом случае говорят, что уравнение движения не удается проинтегрировать, и решение уравнений находят путем численного интегрирования.

Источник

Момент инерции материальной точки и твердого тела: формулы, теорема Штейнера, пример решения задачи

Количественное изучение динамики и кинематики вращательного движения предполагает знание момента инерции материальной точки и твердого тела относительно оси вращения. Рассмотрим в статье, о каком параметре идет речь, а также приведем формулу для его определения.

Общие сведения о физической величине

Сначала дадим определение момента инерции материальной точки и твердого тела, а затем покажем, как его следует использовать при решении практических задач.

Под указанной физической характеристикой для точки, имеющей массу m, которая вокруг оси вращается на расстоянии r, подразумевается следующая величина:

Вам будет интересно: Формулы момента силы для статики и динамики. Работа момента силы

Откуда следует, что единицей измерения изучаемого параметра являются килограммы на квадратный метр (кг*м²).

Если вместо точки вокруг оси вращается тело сложной формы, которое имеет произвольное распределение массы внутри себя, то его момент инерции определяется так:

I = ∫m(r² * dm) = ρ * ∫V(r² * dV).

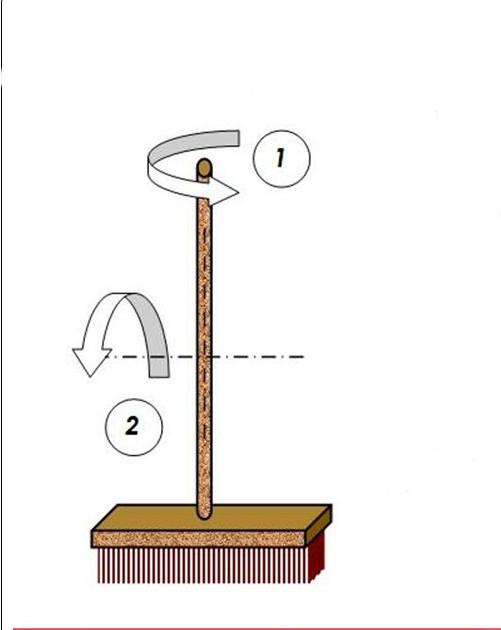
Момент инерции имеет точно такой же смысл для вращения, как масса для поступательного движения. Например, каждый знает, что швабру для мытья полов легче всего вращать вокруг оси, проходящей через ее ручку, чем через перпендикулярную ей. Связано это с тем, что момент инерции в первом случае гораздо меньше, чем во втором.

Величина I для тел разной формы

При решении задач по физике на вращение часто необходимо знать момент инерции для тела конкретной геометрической формы, например, для цилиндра, шара или стержня. Если применить записанную выше формулу для I, то несложно получить соответствующее выражение для всех отмеченных тел. Ниже приведены формулы для некоторых из них:

стержень: I = 1 / 12 * M * L²;

цилиндр: I = 1 / 2 * M * R²;

сфера: I = 2 / 5 * M * R².

Здесь приведены I для оси вращения, которая проходит через центр массы тела. В случае цилиндра ось параллельна генератрисе фигуры. Момент инерции для других геометрических тел и вариантов расположения осей вращения можно найти в соответствующих таблицах. Заметим, что для определения I разных фигур достаточно знать всего один геометрический параметр и массу тела.

Теорема Штейнера и формула

Момент инерции можно определить, если ось вращения расположена на некотором расстоянии от тела. Для этого следует знать длину этого отрезка и величину IO тела относительно проходящей через центр его массы оси, которая должна быть параллельна рассматриваемой. Устанавливающая связь между параметром IO и неизвестным значением I закрепляется в теореме Штейнера. Момент инерции материальной точки и твердого тела математически записывается следующим образом:

Теорема Штейнера значительно облегчает определение I для многих практических ситуаций. Например, если необходимо найти I для стержня длиной L и массой M относительно оси, которая проходит через его конец, то применение теоремы Штейнера позволяет записать:

I = IO + M * (L / 2)2 = 1 / 12 * M * L2 + M * L2 / 4 = M * L2 / 3.

Можно обратится к соответствующей таблице и увидеть, что в ней приводится именно эта формула для тонкого стержня с осью вращения на его конце.

Уравнение моментов

В физике вращения существует формула, которая называется уравнением моментов. Выглядит она следующим образом:

Уравнение моментов по своему смыслу полностью соответствует второму закону Ньютона. При этом I играет роль инерционной массы.

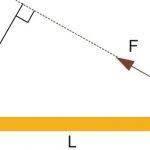
Пример решения задачи

Вообразим себе систему, которая представляет собой цилиндр, закрепленный на вертикальной оси с помощью невесомого горизонтального стержня. Известно, что ось вращения и главная ось цилиндра параллельны друг другу, и расстояние между ними равно 30 см. Масса цилиндра составляет 1 кг, а его радиус равен 5 см. На фигуру действует касательная к траектории вращения сила в 10 Н, вектор которой проходит через главную ось цилиндра. Необходимо определить угловое ускорение фигуры, которое будет вызывать эта сила.

Для начала вычислим момент инерции I цилиндра. Для этого следует применить теорему Штейнера, имеем:

I = IO + M *d² = 1 / 2 * M * R² + M * d² = 1 / 2 * 1 * 0,05² + 1 * 0,3² = 0,09125 кг*м².

Прежде чем пользоваться уравнением моментов, необходимо определить момент силы M. В данном случае имеем:

M = F * d = 10 * 0,3 = 3 Н*м.

Теперь можно определить ускорение:

α = M/I = 3/0,09125 ≈ 32,9 рад/с².

Рассчитанное угловое ускорение говорит о том, что каждую секунду скорость цилиндра будет увеличиваться на 5,2 оборота в секунду.

Источник

Физика Б1.Б8.

Электронное учебное пособие по разделу курса физики Механика

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

Введение

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.

Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).

Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.

Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.

Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.

Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.

Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.

Источник