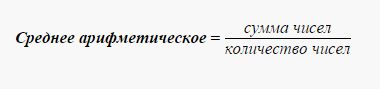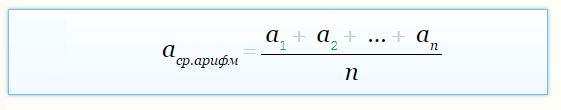Для чего нужно среднее арифметическое чисел
Для чего нужно среднее арифметическое чисел
Средним арифметическим нескольких величин является отношение суммы этих величин к их количеству.
Среднее арифметическое определенного ряда чисел называется сумма всех этих чисел, поделенная на количество слагаемых. Таким образом, среднее арифметическое является средним значением числового ряда.
Чему равно среднее арифметическое нескольких чисел? А равно они сумме этих чисел, которая поделена на количество слагаемых в этой сумме.
Как найти среднее арифметическое число
В вычислении или нахождении среднего арифметического нескольких чисел, нет ничего сложного, достаточно сложить все представленные числа, а полученную сумму разделить на количество слагаемых. Полученный результат и будет средним арифметическим этих чисел.
Рассмотрим этот процесс более подробно. Что же нам нужно сделать для вычисления среднего арифметического и получения конечного результата этого числа.
• Во-первых, для его вычисления нужно определить набор чисел или их количество. В этот набор могут входить большие и маленькие числа, и их количество может быть каким угодно.
• Во-вторых, все эти числа нужно сложить и получить их сумму. Естественно, если числа несложные и их небольшое количество, то вычисления можно произвести, записав от руки. А если же набор чисел впечатляющий, то лучше воспользоваться калькулятором или электронной таблицей.
• В-третьих, необходимо подсчитать количество чисел, входящих в список. При повторе числа, следует каждое из них считать по отдельности.
• И, в-четвертых, полученную от сложения сумму необходимо разделить на количество чисел. В итоге мы получим результат, который и будет средним арифметическим числом этого ряда.
Для чего нужно среднее арифметическое
Среднее арифметическое может пригодиться не только для решения примеров и задач на уроках математики, но для других целей, необходимых в повседневной жизни человека. Такими целями может служить подсчет среднего арифметического для расчета среднего расхода финансов в месяц, или для подсчета времени, которое вы тратите на дорогу, также для того чтобы узнать посещаемость, производительность, скорость движения, урожайность и много другого.
Так, например, давайте попробуем рассчитать, сколько времени вы тратите на дорогу в школу. Идя в школу или возвращаясь, домой вы каждый раз тратите на дорогу разное время, так как когда вы спешите, то вы идете быстрее, и поэтому дорога занимает меньше времени. А вот, возвращаясь, домой вы можете идти не спеша, общаясь с одноклассниками, любуясь природой и поэтому времени на дорогу займет больше.
Поэтому, точно определить время, затраченное на дорогу у вас не получиться, но благодаря среднему арифметическому вы сможете приблизительно узнать время, которое вы тратите на дорогу.
Припустим, что в первый день после выходных, вы потратили на путь от дома до школу пятнадцать минут, на второй день ваш путь занял двадцать минут, в среду вы прошли расстояние за двадцать пять минут, за такое же время составил ваш путь и в четверг, а в пятницу вы никуда не торопились и возвращались целых пол часа.
Давайте найдем среднее арифметическое, прибавив время, за все пять дней. Итак,
15 + 20 + 25 + 25 + 30 = 115
Теперь разделим эту сумму на количество дней
Благодаря такому способу вы узнали, что путь от дома до школы вы приблизительно тратите двадцать три минуты своего времени.
Домашнее задание
1.Путем нехитрых вычислений найдите среднее арифметическое число посещаемости учеников вашего класса за неделю.
Общие сведения
Понятие среднеарифметической величины впервые предложил древнегреческий ученый — Пифагор. Позднее этот термин стал использоваться в математике. Чтобы понять его смысл, необходимо получить базовые знания о числовых значениях. Они делятся на 2 вида:
Первый тип — натуральные числа, они применяются при устном счете предметов.
Дробные бывают также двух типов:
Десятичные дроби делятся на конечные, периодические и непериодические бесконечные. Первый тип состоит из целой и дробной частей, разделенных между собой запятыми. Как правило, количество разрядов ограничено определенным значением. Если рассматривать бесконечные периодические десятичные дробные выражения, они состоят из множества элементов. Последние повторяются с определенной периодичностью. Например, 5,(321), где величина периода указывается в круглых скобках.
В случае когда дробное тождество является бесконечным непериодическим, очень часто представление осуществляется в форме обыкновенной дроби. Последняя состоит из делимого и делителя, отделенных друг от друга косой чертой «/». Первый элемент именуется числителем, а второй — знаменателем.
Обыкновенные дробные выражения бывают правильными, неправильными, а также могут записываться в форме смешанного числа, т. е. величины, состоящей из целого компонента и обыкновенной правильной дроби.
Перед подсчетом значения среднего арифметического в 5 классе специалисты рекомендуют ознакомиться с алгоритмом работы со смешанными величинами.
Смешанные числа
Смешанные числа являются промежуточными величинами между обыкновенными дробями и целыми. Не каждое дробное тождество можно представить в таком виде. Для этого подойдет только неправильное выражение. Алгоритм преобразования:
Методика обратной конвертации смешанного числа в неправильное дробное выражение является еще одной операцией, о которой нужно знать. Ее реализация:
Специалисты рекомендуют начинающему математику потренироваться, придумывая различные задания на конвертацию числовых выражений.
Далее необходимо перейти непосредственно к определению, позволяющему расшифровать, что значит среднее арифметическое чисел, а также к самой методике расчета искомой величины.
Алгоритм нахождения среднего значения
Среднее арифметическое — математическая характеристика, позволяющая найти оптимальное значение.
Например, на уроках выставляется оценка за месяц. Для ее вычисления необходимо найти среднее значение всех отметок, полученных учеником.
Кроме того, среднее арифметическое используется при вычислении какой-либо характеристики опытным путем.
Например, при расчете заряда электрона производится определенное количество измерений, а затем рассчитывается средняя величина заряда частицы.
Методика определения среднеарифметического значения:
Для реализации алгоритма на практике необходимо записать несколько чисел — 4, 7, 8, 12, 15. Решение выглядит следующим образом:
В некоторых случаях результат необходимо округлять. Однако этого можно не делать при подсчете какой-либо физической величины.
При проведении опытов необходимо брать больше значений, поскольку это существенно влияет на точность получения данных.
Пример решения
Для закрепления теории необходимо разобрать пример и решить его. Например, нужно найти среднее арифметическое четырех смешанных чисел, а именно: 3 2/3, 4 5/7 и 6 3/8.
Решение выполняется по следующему алгоритму:
При получении результата в виде неправильной дроби, его нужно преобразовать в смешанную величину. Это считается «правилом хорошего тона» в математике, поскольку любой ответ должен переводиться в читабельную сокращенную форму.
Кроме того, можно проверить результат выполнения операции, воспользовавшись онлайн-сервисами. Однако пользоваться ими часто не рекомендуется, поскольку нужно уметь искать ошибки самостоятельно.
Таким образом, для вычисления среднеарифметического значения необходимо знать специальную методику, предложенную специалистами в области математики.
Для чего нужно среднее арифметическое чисел
“Мы живем, влюбляясь и мечтая,
Падая и поднимаясь ввысь.А статистика упрямая стараетсяВ цифрах выразить всю нашу жизнь”.
Выяснить в каких сферах общественности применяется среднее арифметическое значение.
Для достижения поставленной цели необходимо решить следующие задачи:
Рассказать о взаимосвязи статистики и сфер жизни
Показать, как среднее арифметическое применяется при решении задач связанных с различными областями человеческой деятельности.
Предмет исследования – применение среднего арифметического в различных областях человеческой деятельности.
Статические методы применяются во многих областях жизни при анализе различных ситуаций. Статистика не только определяет равномерность явлений, а также позволяет их тщательно изучать в частности.
В настоящее время статистика имеет следующее определение. Статистика – это планомерный и систематический учет массовых общественных явлений, который осуществляется государственными статистическими органами и дает числовое выражение проявляющимся закономерностям. Статистик существует очень много, например: статистика промышленности, статистика торговли, экономическая статистика, математическая, прикладная и т.д.
Основными задачами статистического исследования являются выявление и анализ закономерностей объектов которые выбраны для исследования, с целью установления возможности и достоверности перенесения сделанных выводов на генеральную совокупность.
Наше исследование является актуальным, так как многие люди в своей профессии часто используют методы статистики, в частности – вычисление среднего арифметического значения, не задумываясь об этом, и мы в своей работе решили акцентировать ваше внимание, чтобы показать, насколько этот метод важен в различных областях жизнедеятельности человека
Каждый из нас может применяет методы статистики в своей деятельности. Чтобы серьезно подойти к решению проблемы необходимо проанализировать ситуацию и сделать соответствующие выводы Статистические методы применяются в правоохранительных органах, здравоохранении, образовании, производстве и продаже товаров, в сфере услуг и т.д. Все статистические методы связаны с подсчетом тех или иных данных.А это означает, что статистика является одним из важнейших разделов математики, а математика как мы знаем наука о структурах, порядке и отношениях, которая сложилась на основе операций подсчёта, измерения и описания свойств и форм объектов. Математика не относится к естественным наукам, но широко используется в них как для точной формулировки их содержания, так и для получения новых результатов. Математика — наука, которая предоставляет данные другим наукам.
Статистика- это наука, изучающая количественную сторону массовых общественных явлений и процессов в неразрывной связи с их качественными особенностями в конкретных условиях места и времени. Это универсальная наука, охватывающая все отрасли человеческой деятельности. Для изучения тех или иных явлений в статистике применяют различные методы. Одним из важнейших методов является метод нахождения среднего арифметического. Не менее важную роль в исследование данных вносят медиана, размах, и мода.
Среднее арифметическое (средним арифметическим ряда чисел называется частное от деления суммы этих чисел на их количество) является важной характеристикой ряда чисел
Статистические данные применяются постоянно во всех сферах жизни, так же как и статистические методы, которые обеспечивают сбор необходимых данных. Основу статистики должны знать все люди, так как эта наука обучает, как собирать и систематизировать их, а также анализировать и делать выводы. В жизни подобные знаний могут пригодиться и не раз, причем на любой работе. У каждого человека есть свой метод анализа окружающего мира, а статистика помогает формировать наблюдательность, которая нужна при сборе информации. Статистика позволяет регистрировать социальные, демографические, экономические и т.д. феномены.
В своей работе я хочу показать где и как применяется среднеарифметическое в различных областях жизни. Для этого я обращалась к медицинским учебникам, интернет-данным, проанализировала результаты гиа за некоторые годы учащихся нашей школы и дневник наблюдений за погодой, который вела сама в 6 классе. Остановимся более подробно на исследовании
Теоретическая часть.
Применение среднеарифметического в медицине.
Медицинская статистика является методом социальной диагностики, поскольку она позволяет дать оценку состояния здоровья населения страны, региона и на этой основе разработать меры, направленные на улучшение общественного здоровья. Важнейшим принципом статистики является применение ее для изучения неотдельных, единичных, а массовых явлений, с целью выявления их общих закономерностей. Эти закономерности проявляются, как правило, в массе наблюдений, то есть при изучении статистической совокупности.
1) позволяет количественно измерить показатели здоровья населения и показатели деятельности медицинских учреждений
2) определяет силу влияния различных факторов на здоровье населения
3) определяет эффективность лечения и оздоровительных мероприятий
4) позволяет оценить динамику показателей здоровья и позволяет прогнозировать их
5) позволяет получить необходимые данные для разработки норм и нормативов здравоохранения.
Средние арифметическое используются в медицине и здравоохранении:
а) для оценки состояния здоровья — например, параметров физического развития (средний рост, средний вес, средний объем жизненной емкости легких и др.), соматических показателей (средний уровень сахара в крови, средний пульс, средняя СОЭ и др.);
б) для оценки организации работы лечебно-профилактических и санитарно-противоэпидемических учреждений, а также деятельности отдельных врачей и других медицинских работников (средняя длительность пребывания больного на койке, среднее число посещений за 1 ч. приема в поликлинике и др.);
в) для оценки состояния окружающей среды.
В то же время, у больных людей значения многих физиологических параметров имеют асимметричное распределение, ввиду того, что изменяются в сторону увеличения или уменьшения под влиянием заболевания. Поэтому для характеристики центральной тенденции их распределения помимо среднего арифметического используется медиана, мода и размах ряда величин.
Применение среднеарифметического в органах правоохранения
Статистика в органах правоохранения охватывает широкий круг проблем, связанных с негативными явлениями в обществе. Изучает различного рода преступления и правонарушения, такие как: бандитизм, ограбление, изнасилование, проституция, наркомания, алкоголизм, коррупция и другие отрицательные общественные явления, а так же нарушения морально-этических норм. Статистика изучает не только негативные явления, но и позитивные, которые характеризуют моральный облик людей. Статистический анализ начинается с изучения показателей, взятых из отчетов. Прежде всего определяется уровень преступности, т. е. выясняется, сколько в абсолютных цифрах зарегистрировано преступлений— всего, а также по родам и видам. Аналогичную характеристику в абсолютных цифрах получают о лицах, совершивших эти преступления (их общее число, по видам совершенных преступлений, по признакам пола, возраста, социального положения и т. д.), об объеме и структуре деятельности правоохранительных органов и других субъектов борьбы с преступностью. В криминологических исследованиях средние показатели применяют, например, для определения среднего возраста преступников, средних сроков наказания, назначенных за какой-либо вид преступления. Также, представляет интерес степень распространенности преступности среди различных возрастных групп, среди специальных субъектов преступлений (работников торговли, автотранспорта), среди групп населения, выделенных породу занятий, отрасли народного хозяйства, типу населенного пункта, времени проживания в данной местности, и т. д. Криминологическая статистика дает возможность наиболее оптимально спланировать распределение сил и средств борьбе с преступными проявлениями. Исходя из статистических показателей с уровнем преступности, возможностей оперативных и следственных работников и других данных, планируется средняя штатная численность правоохранительных органов и их допустимая средняя индивидуальная нагрузка.
Применение среднеарифметического в образовании
Применение среднеарифметического в оценке условий жизни населения страны.
Уровень жизни населения — представляет собой экономическую категорию. Это уровень обеспеченности населения необходимыми материальными благами и услугами. Уровень жизни — это уровень благосостояния населения, потребления благ и услуг, совокупность условий и показателей, характеризующих меру удовлетворения основных жизненных потребностей людей.
В настоящее время, когда экономические системы стран подвергаются деформации и видоизменяются главной целью остаётся осуществление принципа социальной направленности рыночной экономики с помощью улучшения уровня жизни населения.
Основными задачами статистики уровня жизни населения являются: изучение фактического благосостояния населения, а также факторов, определяющих условия жизнедеятельности граждан страны в соответствии с экономическим ростом; измерение степени удовлетворения потребностей в материальных благах и услугах во взаимосвязи с социальными условиями и развитием производства.
Базой для построения системы показателей и решения указанных задач являются материалы макроэкономической статистики, демографической статистики, статистики труда, торговой статистики, статистики цен. Значительный объем собираемых сведений основывается на данных финансовой и бухгалтерской отчетности, государственной налоговой службы, Центрального банка РФ, Пенсионного фонда РФ и др., а также на материалах специальных обследований, переписей, опросов.
Здесь средние величины обобщают качественно разнородные значения признаков или системных пространственных совокупностей (международное сообщество, континент, государство, регион, район и т.д.) или динамических совокупностей, протяженных во времени (век, десятилетие, год, сезон и т.д.). средний национальный доход на душу населения, средняя урожайность зерновых по всех стране, средний реальный доход на душу населения, среднее потребление продуктов питания на душу населения, производительность общественного труда).
Очень заметна польза статистики в экономике. Учитывая то, что все в нашем мире продается и покупается, каждый норовит создать свой бизнес, то без анализа рынка никак
В настоящее время экономика нашей страны зависит от соотношения доллара и рубля. Резкое падение российского рубля произошло в декабре 2014 года.
Такие колебания курса рубля не новое явление и весьма характерное для финансовой истории России. 15 и 16 декабря 2014 года рубль упал на 22 процента
по отношению к ведущим мировым валютам, что побудило правительство и ЦБ РФ принять экстренные меры для спасения российской национальной валюты.
Впечатляющее падение рубля на 22 процента 15 декабря и 16 декабря также побудило инвесторов воспринять ситуацию как повторение кризиса 1998 года, когда рубль потерял 27 процентов 17 августа. Рубль в 2014 году упал более чем на 40 процентов по отношению к доллару и достиг новых исторических минимумов. К началу 2015 года, рубль находился на отметке 56,24 по отношению к доллару по сравнению с 32,9 в начале 2014 года.
Применение среднеарифметического в климатологии.
Показателями отдельных метеорологических элементов являются: средние значения, крайние значения, амплитуды, повторяемость различных значений элементов, накопленная повторяемость (обеспеченность), показатели изменчивости, показатели асимметрии и крутости кривой распределения.
Средние значения. Обычно определяют средние значения температуры и влажности воздуха, скорости ветра, атмосферного давления, осадков и т. д.
Чаще других определяют средние суточные, месячные и годовые значения метеорологических элементов.
Средняя месячная температура – деление сумы средних суточных температур на число суток месяца.
Практическая часть.
Применение среднеарифметического в медицине.
1.В травматологический пункт поликлиники №4 г.Волгограда в течение месяца ежедневно обращалось следующее число больных:
Среднее арифметическое: физический смысл и визуализация
Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:
Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.
Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.
Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.
Среднее арифметическое двух чисел
Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:
Их среднее арифметическое:
Физический смысл среднего арифметического
Изобразим два исходных числа и их среднее арифметическое на числовой оси:
Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.
В механике момент силы – это произведение силы F на расстояние l:
На плечи весов действует сила, создаваемая весом точек-«грузов». Обозначив расстояния от грузов до точки опоры l1 и l2, получим:
Точки-«грузы» отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:
Обозначив m координату точки опоры весов, получим:
Аналогично из формулы равенства моментов для произвольного количества N точек-«грузов» с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:
Координата опоры весов m:
Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.
Визуальное восприятие равновесия
Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.
Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:
На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.
Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:
Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.
Математическое ожидание случайной величины
Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-«груза». Формула равенства моментов с разными весами:
Теперь точка опоры весов в равновесии это μ:
Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:
Это и есть формула математического ожидания.
Гистограмма
Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.
На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.
Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:
Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:
Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:
Дайте мне точку опоры, и я переверну Землю. Архимед