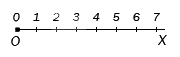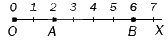Для чего нужно уметь сравнивать числа
«Сравнение многозначных чисел»
Просмотр содержимого документа
«»Сравнение многозначных чисел»»
Тема урока: Сравнение многозначных чисел
Тип урока: урок усвоения новых знаний и первичного закрепления знаний.
Формы работы на уроке: индивидуальная, фронтальная.
Цель урока: Научить сравнивать числа, состоящие из единиц I и II классов; совершенствовать устные и письменные вычислительные навыки.
Обучающие: научить сравнивать многозначные числа.
Развивающие: развивать логическое мышление, математическую речь, умение сравнивать и обобщать; развивать самостоятельность учащихся, умения преодолевать трудности в учении, используя различные задания.
Воспитательные: воспитывать ответственное отношение за результат своего труда, воспитывать интерес к математике, аккуратность.
Оборудование урока: учебник математика М.И. Моро; маршрутные листы.
− Здравствуйте. Все готовы к работе? Садитесь, пожалуйста!
− Ребята, на уроке нас ждёт много интересной работы. Мы будем узнавать новое, исследуя старое; доказывать и спорить, радоваться вместе нашим победам, и с неудачами справляться тоже вместе.
— Каждый из вас получил лист достижений, в котором будет отмечать свои успехи на уроке. Подпишите его и отметьте свое настроение в начале урока.
− Итак, мы начинаем! Открываем тетради и пишем сегодняшнее число, классная работа.
III. Актуализация знаний.
− А начнём наш урок с «зарядки для ума». И в этом мне поможет Кристина (ученица). Она будет диктовать числа, а вы у себя в тетрадях через запятую будете записывать их цифрами:
Учащиеся записывают в тетрадях числа под диктовку, потом проверяют:
шестьдесят четыре; 64
четыреста двадцать пять; 425
восемь тысяч двести пять; 8205
триста шестьдесят пять тысяч сто; 365 100
сто сорок шесть; 146
девять тысяч шестьдесят; 9060
запишите число, предшествующее числу 70000; 69999
запишите число, предшествующее числу 7000; 6999
запишите число, следующее за числом 8000; 8001
− А теперь поменяйтесь тетрадями и проверьте друг у друга.
Взаимопроверка арифметического диктанта:
– Поднимите руки те, у кого всё правильно. Молодцы!
– А у кого 1-2 ошибки?
– А есть ли у нас те, у кого больше 5 ошибок?
− Кто не справился с заданием, в следующий раз будьте внимательны. У вас обязательно всё получится.
III.Самоопределение к деятельности
— Тема нашего урока: Сравнение многозначных чисел.
— Для чего нужно уметь сравнивать многозначные числа? (ответы учащихся)
— Цель нашего урока: Вывести правило сравнения чисел и научиться его применять.
—Сформулируйте задачи урока. (Научиться сравнивать многозначные числа)
− Правильно, сегодня на уроке мы с вами узнаем, как сравнивать многозначные числа. А поможет в этом нам Илья (ученик выходит и объясняет).
-Сделайте вывод: какие способы сравнения мы с вами знаем? (Чем больше цифр в записи числа, тем оно больше. Чем правее стоит число в натуральном ряду, тем оно больше. Если в записи числа одинаковое количество цифр, сравнивать начинаем с большего разряда.).
IV.Работа по теме урока.
-А теперь давайте откроем учебники и прочитаем текст рядом с красной чертой на с 27.
1. Из двух чисел меньше то, которое при счете называют раньше, и больше то, которое называют позже.
2. Сравниваем числа поразрядно, начиная с высших разрядов.
-Какими способами мы сравнивали числа?
Выполнение №117 (с.27)
-Какими способами мы сравнивали числа?
(Чем левее число расположено в натуральном ряду, тем оно меньше.
Сравниваем числа поразрядно, начиная с высших разрядов).
− Прежде, чем продолжить урок, предлагаю немного отдохнуть.
-Когда я говорю однозначные числа: приседаем
Двузначные числа: руки вверх.
Трехзначные числа: хлопаем в ладоши
VI.Закрепление изученного материала.
Запиши числа в таблицу в порядке возрастания и убывания
Конспект урока по математике «Учимся сравнивать числа»
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Тема урока: Как можно сравнивать числа
Тип урока: овладение новыми знаниями.
Цель: Формировать умение сравнивать двузначные числа разными способами.
формировать умение сравнивать двузначные числа с опорой на их десятичный состав.
способствовать развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления.
Личностные:способность к самооценке на основе критерия успешности учебной деятельности.
Регулятивные УУД:умение определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действий на уровне адекватной оценки; планировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; высказывать свое предположение.
Коммуникативные УУД:умение оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им.
Познавательные УУД:умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.
Основные понятия: уменьшилось, увеличилось
Межпредметные связи: математика, чтение.
Основные:Башмаков М.И., Нефедова М.Г., Математика. Учебник для 1 класса, часть 2, стр. 28-29
Дополнительные: презентация к уроку, проектор, печатные картинки для фронтальной работы.
Организация пространства: фронтальная работа, индивидуальная работа, работа в парах.
В планировании и проведении урока учитель играет ведущую роль. Я включаю детей в конструктивную деятельность, побуждаю их к открытию новых знаний, учу ребят ставить цели, искать пути их достижения, ставлю перед детьми учебную задачу и совместно решаем её.
Направляю содержание урока в рамки гуманно-личностного, нравственного обучения и воспитания. Формирую эмоционально-коммуникативный компонент урока. Развиваю у ребят умение адекватно реагировать на трудность, не бояться ошибок. Развиваю навыки самоконтроля, адекватную самооценку, эмпатию, партнёрство и сотрудничество.
Учащиеся класса, в целом, имеют адекватную, нормативную самооценку своих сил, возможностей, знаний, умений и навыков. Преобладают широкие познавательные мотивы, мотивы достижения и социального признания. Высокий уровень сформированности нравственных качеств. Ребята умеют ставить перед собой цели, знают пути их достижения. Принимают и удерживают учебную задачу, могут прогнозировать результат деятельности. Осуществляют контроль над своей деятельностью и поведением. Развиты навыки саморегуляции. Коммуникативные навыки развиты в соответствии возраста детей. Ребята с радостью сотрудничают, как с учителем, так и друг с другом. Умеют слушать и слышать. С уважением относятся как взрослым, так и к сверстникам. Способны конструктивно разрешать конфликты.
Технологическая карта урока.
1.Мотивация к учебной деятельности.
-актуализация требований к ученику со стороны учебной деятельности;
-создание условий возникновения у учащихся внутренней потребности включения в учебную деятельность;
-способствовать положительному эмоциональному настрою на плодотворную работу, снятие психоэмоционального напряжения, установлению коммуникативного контакта.
За окном темно, морозно, а в классе тепло от ваших сердец и светло от искорок в ваших глазах. Все это поможет нам успешно поработать на уроке. А что еще необходимо для успешной работы на роке?
Девизом нашего урока будут слова « С малой удачи начинается большой успех.».
-Как вы понимаете эти слова?
Уметь оформлять свои мысли в устной речи. Уметь слушать и понимать речь других. (Коммуникативные)
2.Актуализация опорных знаний.
-организация выполнения учащимися пробного учебного действия;
-организация фиксирования учащимися индивидуального затруднения.
Данный этап мотивирует учащихся на расширение границ своих знаний по предлагаемой теме.
Осуществляется осознание цели и задачи.
Активизируются мыслительные процессы: анализ, синтез, обобщение.
— Катя и Таня задумали два числа.
Назовите соседей этого числа. (81 и 83)
Какое это число четное или нечетное? ( четное)
Сколько в нем десятков и единиц? (8д.2ед.)
Увеличьте его на 2. (84)
Игра «Третий лишний».
Какое число лишнее? Обоснуйте свой ответ.
Что общего у этих чисел? ( Состоят из одни х и тех же цифр, двузначные, нечетные, сумма цифр равна 4)
-Чем отличаются?( Порядок цифр при записи числа)
-Объясните, почему при использовании одних и тех же цифр получили разные числа?(Стоят в разных разрядах)
Сравните числа 13 и 31. ( по порядку названия при счете, по числовому лучу.)
Уметь проговаривать последовательность действий на уроке. ( Регулятивные УУД)
Уметь преобразовывать информацию из одной формы в другую, ориентируясь в системе знаний (Познавательны
3.Формулирование темы урока, постановка цели.
-организовать формулирование темы урока учащимися с помощью учителя;
-постановка цели урока детьми..
-А знаете другие способы сравнения чисел? (Проблемный вопрос)
Тема урока: Как можно сравнивать числа.
_Какую учебную задачу можем поставить? ( Научиться сравнивать числа разными способами).
-Прежде чем приступить к выполнению этой задачи нам нужно набраться сил.
Физминутка для глаз
С помощью учителя формулируют тему и цели урока.
определение и осознание того, что уже известно и что нужно усвоить;
планирование – составление плана и последовательности действий;
Уметь оформлять свои мысли в устной форме (Коммуникативные УУД).
Уметь ориентироваться в своей системе знаний:
отличать новое от уже известного с помощью учителя (Познавательные
УУД). Умение определять и формулировать цель на уроке при помощи учителя. (Регулятивные УУД)
4.Работа над новым материалом.
— реализовать построенный проект в соответствии с планом;
— зафиксировать новые знания в речи;
-организовать устранение и фиксирование преодоления затруднения.
-Вспомните, как сравнивают числа с помощью числового луча.
Сравните с помощью числового луча числа 9 и 10.
-посмотрите на доску. Что вы видите?( Числовой луч)
Разместите шарики с числами на этом числовом луче.
-Что вы заметили?( Однозначные числа левее двузначных)
-Какой вывод можем сделать?
(Однозначное число всегда меньше двузначного)
-Сравните наш вывод с выводом в учебнике после задания №2.
Совпадает? Правы мы?.
-А как записать это с помощью математических знаков?
Дети с помощью учителя отвечают на поставленные вопросы.
Сравнивают числа с помощью модели числового луча.
Выбирают запись к составленному рассказу и рисунку.
Рассуждают, объясняют и делают вывод.
Уметь добывать новые знания: находить ответы на вопросы, используя учебник, свой жизнен- ный опыт и информацию, полученную на уроке (Познавательные УУД). Уметь оформлять свои мысли в устной форме; слушать и понимать речь других (Коммуникативные УУД). Работают по коллективно составленному плану (Регулятивные УУД).
Уметь преобразовывать информацию из одной формы в другую, ориентируются в ситуации.
Уметь слушать и понимать речь других (КоммуникативныеУУД)
5.Продолжение работы по теме.
-Ребята есть еще один способ сравнения чисел.
-Узнаем мы о нем из задания №3.
-Кого видите на рисунках?(Гномиков).Они живут под землей и охраняют подземные богатства.
-В мешках у гномиков изумруды.
-Какой гномик набрал больше всех изумрудов? (красный)
-Какой меньше всех? (зеленый)
-Какие цифры помогли вам это определить? Что они обозначают в числах (количество десятков)
Сделайте вывод, вставив нужное слово в предложение.(Чем больше десятков в числе, тем…двузначное число.)
— Прежде чем выполнить следующее задание, выполним ФИЗМИНУТКУ. Приготовьте суджоку. Встаньте.
Дети с помощью учителя отвечают на поставленные вопросы.
Выбирают запись к рисунку.
Рассуждают, объясняют и делают вывод о новом способе сравнения двузначных чисел ( по количеству десятков).
усвоение учениками нового способа действий с проговариванием во внешней речи.
Освоение способа действий.
-Молодцы! Проверим, как вы сможете применить ваши знания.
Дети выполняют задание и объясняют выбранный результат.
Затем самостоятельно выполняют задание, записывая в тетрадь..
Ребята анализируют, классифицируют, сравнивают, аргументируют, моделируют, оценивают результат своей деятельности.
Работа в парах. Соотнесение с эталоном.
Уметь проговаривать последовательность действий на уроке (Регулятивные УУД).
Уметь оформлять свои мысли в устной и письменной форме; слушать и понимать речь других (Коммуникативные УУД).
Пропедевтика решения задач
6.Самостоятельная работа с самопроверкой по эталону
-организовать выполнение учащимися самостоятельной работы на новое знание;
— организовать взаимопроверку по эталону, самооценку;
На данном этапе преобладают специфические познавательные эмоциональные, социальные мотивы. Чётко прослеживается многоуровневость взаимодействия: «ученик – учитель», «ученик – ученик».
3и 4 столбики- самостоятельно выполнить в тетради.
Вам предстоит работа в тетради, поэтому вспомните правила
-молодцы! Вы успешно справились с заданием. Теперь вы умеете сравнивать числа?
-Проверим это, используя задание №5 в учебнике.
Какое число предметов обозначает пучок редисок? (10)
Сколько редисок на левом рисунке?
Каким числом обозначим это количество? (35)
Запишем это число в тетради.
Отступите 2 клеточки напишите по середине листа №5. Через 1 клеточку в начале строки поставили точку. Запишите число35.
Ск. редисок на правом рисунке?
Отступив вправо 1 клеточку, запишите самостоятельно каким числом вы это обозначите.
-Что вы заметили?(Количество десятков одинаковое)
-Используя известные способы сравнения чисел сравните эти числа. Расскажите, кто какой способ использовал.
Подходят эти способы в данной ситуации? (Нет)
-Какой можем сделать вывод?
(если число десятков в числах одинаковое, то больше то число, в котором больше количество единиц)
Дети самостоятельно выполняют задание.
Дети работают в паре, проверяя задание.
Сверяют результат с эталоном на доске.
С опорой на рисунок самостоятельно выводят правило сравнения чисел, в которых количество десятков одинаково.
Уметь проговаривать последовательность действий на уроке (Регулятивные УУД).
Уметь планировать своё действие в соответствии с поставленной задачей (Регулятивные УУД).
Уметь вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок(РегулятивныеУУД).
Способность к самооценке на основе критерия успешности учебной деятельности (Личностные УУД).
Развиваютя коммуникативные навыки, самоконтроль
7.Рефлексия учебной деятельности на уроке
— зафиксировать новое содержание урока;
-организовать рефлексию и самооценку учениками собственной учебной деятельности.
Выбранный способ контроля является целесообразным, соответствует индивидуальным, возрастным особенностям детей, особенностям класса, строящего своё обучение и воспитание на гуманно-нравственной основе
— Наш урок подходит к концу.
-Что нового вы узнали?
— Что поняли и запомнили?
-Какую цель ставили перед собой?.
-Какие способы сравнения чисел мы теперь знаем?
По порядку называния при счете.
По количеству знаков в записи числа.
По количеству десятков.
По количеству единиц, если количество десятков одинаково.
Ребята, спасибо вам за работу, а ваша награда – полученные знания и сделанные вами открытия!
Дети понимают критериальную базу оценки личностных, метапредметных и предметных результатов урока.
Уметь проговаривать последовательность действий на уроке (Регулятивные УУД).
Уметь планировать своё действие в соответствии с поставленной задачей (Регулятивные УУД).
Уметь вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок(РегулятивныеУУД).
Способность к самооценке на основе критерия успешности учебной деятельности (Личностные УУД).
Пропедевтика решения задач (Познавательные УУД)
Развиваютя коммуникативные навыки, самоконтроль
Сравнение натуральных чисел: равно или не равно, больше или меньше?
Сравнение натуральных чисел между собой – тема данной статьи. Разберем сравнение двух натуральных чисел и изучим понятие равных и неравных натуральных чисел. Выясним большие и меньшие из двух чисел на примерах. Поговорим о натуральном ряде чисел и об их сравнении. Будут показаны результаты сравнений трех и более чисел.
Сравнение натуральных чисел
Рассмотрим это на примере. Когда на дереве имеется стая, состоящая из 7 птиц, а на другом из 5 десятка птиц, то стаи считаются разными, так как не похожи друг на друга. Отсюда можно делать вывод о том, что эта непохожесть и есть сравнение.
При сравнении натуральных чисел проводится такая проверка на похожесть.
Если считать, что под сравнением натуральных чисел подразумевают действие, то оно может привести к нескольким результатам:
Когда получаем неравенство, это значит, что одно из этих чисел больше или меньше другого, что и увеличивает диапазон использования натуральных чисел.
Рассмотрим определения равных и неравных чисел. Разберем, каким образом это определяется.
Равные и неравные натуральные числа
Рассмотрим определение равных и неравных чисел.
В случае, когда записи двух натуральных чисел одинаковы, их считают равными между собой. Когда записи имеют различия, тогда эти числа неравные.
Сравнение однозначных натуральных чисел
Если в записи имеются два натуральных числа со знаками « » и « > », тогда она называется неравенством. Неравенства могут быть верными и неверными.
Запись 4 7 – верная, а 3 > 9 – неверная.
Сравнение однозначного и многозначного натуральных чисел
Если принять за правило, что все однозначные числа меньше двухзначных, тогда получим:
Рассмотрим сравнения многозначных чисел.
Сравнение многозначных натуральных чисел
Рассмотрим сравнение двух неравных многозначных натуральных чисел с равным количеством знаков. Предварительно следует повторить раздел, изучающий разряды натурального числа и значение разряда.
В таком случае производится поразрядное сравнение, то есть слева направо. Меньшим считается число, которое имеет меньшее значение соответствующего разряда и наоборот.
Чтобы решить пример, нужно уяснить, что 0 всегда меньше любого натурального числа и что он равен самому себе. Число ноль относится к разряду натуральных чисел.
Сравнение многозначных натуральных чисел производится по-другому. Большим числом считают то, которое имеет меньшее количество знаков и наоборот.
Решение
Натуральный ряд чисел, нумерация, счет
Эта запись продолжается до бесконечности. Такая бесконечная последовательность чисел называется натуральным рядом чисел.
Существует еще один процесс – счет. Во время счета числа называются одно за другим, то есть таким образом, как они зафиксированы по ряду. Данный процесс применим для определения количества предметов.
Исли имеется определенное число предметов, но нам необходимо узнать количество, используем счет. Он производится, начиная с единицы. Если во время пересчета перекладывать предметы в кучу, то ее можно назвать натуральным рядом чисел. Последний предмет будет являться числом их количества. Когда процесс закончен, мы знаем их число, то есть предметы пересчитаны.
Во время счета меньше то натурально число, которое находится раньше и называется раньше. Применение нумерации используется для конкретного определения предмета, то есть присваивая ему определенный номер. Например, имеем некоторое количество предметов. На каждом из них зафиксируем их порядковый номер. Таким образом производится нумерация. Она применима для различения одинаковых предметов.
Натуральные числа на координатном луче
Для начала необходимо повторить определение координатного луча.
При просмотре слева направо видим штрихи, которые означают определенную последовательность чисел, начиная от 0 и до бесконечности. Эти штрихи называют точками. Точки, расположенные левее меньше точек, расположенных правее. Отсюда следует, что точка, имеющая меньшую координату на координатном луче, расположена левее точки с большей координатой.
Наименьшее и наибольшее натуральное число
Считается, что 1 – это наименьшее натуральное число из множества всех натуральных чисел. Все числа, расположенные правее него считаются больше предыдущего. Этот ряд бесконечен, поэтому нет наибольшего числа из этого множества чисел.
Двойные, тройные неравенства
Таким же образом выполняются тройные, четверные и так далее неравенства.
Необходимо быть внимательным при составлении двойных неравенств, так как можно произвести его неверно, что повлечет за собой неправильное решение задачи.
Урок математики в 4-м классе «Сравнение чисел»
— Сегодня я вам предлагаю провести очередной тур игры «Что? Где? Когда?» между знатоками 4а и 4б классов. В этом туре вы отвечаете на вопросы знатоков 4а класса. Для проведения игры, которая состоит из четырех раундов, вам необходимо разделиться по группам-командам.
Назовите вариант ответа, в котором цифра 5 стоит в разряде десятков:
Определите правильную запись числа шесть тысяч девять:
Назовите правильную запись числа 975 в виде суммы разрядных слагаемых:
Назовите те выражения, значения которых содержат тридцать десятков (предлагается работа в черновиках):
— С какими числами вы работали? (ответы учащихся);
— Сегодня мы продолжим работу с натуральными числами.
РАБОТА НАД НОВОЙ ТЕМОЙ
«Найти закономерность, заполнить «окошки» в таблице и ответить на вопросы»
СРАВНЕНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ
(запись на мультимедиа)
— Цель нашего урока: Вывести правило сравнения чисел и научиться его применять.
(ЗАПИСЬ в тетради числа, темы урока)
Составление 1 алгоритма сравнения чисел
— Каким способом можно сравнивать числа?
— На какие знания вы опирались при сравнении чисел? (ответы учащихся)
Составление 1 алгоритма
— Чтобы сравнить два числа мы должны сделать первый шаг:
(запись на мультимедиа)
— Значить оно по сравнению с числом 90 будет больше или меньше? (ответы учащихся)
— Значить оно будет больше или меньше? (ответы учащихся)
— Значит, оно будет больше или меньше? (ответы учащихся)
— Значит, оно будет больше или меньше? (ответы учащихся)
Вывод: вы проговорили правило сравнения натуральных чисел с помощью алгоритма. В дальнейшем вы еще не раз будете составлять алгоритмы.
— Для закрепления правила вам предлагается сравнить числа
Закрепление применения 1 алгоритма.
(запись на мультимедиа)
Взаимопроверка в парах, сравнение с правильными ответами.
Закрыли глазки. Вдохнули глубоко. Задержали дыхание, выдохнули. (повторяется 3 раза). Подняли руки вверх, потянулись. Опустили руки на парты.
Зафиксировали взгляд на тренажере и повторили упражнения для глаз. (3 раза)
4) Составление 2 алгоритма сравнения чисел
а) О каких величинах говорится в задаче?
(о времени работы рабочего и ученика, о количестве вытачиваемых деталей рабочим и учеником, об изготовлении за час)
б) Уточним, какие числовые значения соответствуют этим величинам.
Поиск решения задачи.
— Можно ли сразу узнать, на сколько деталей за 1 час больше вытачивает рабочий, чем ученик? (Нет, так как мы не знаем, сколько за 1 час вытачивает рабочий и сколько за 1 час вытачивает ученик)
— Можно ли узнать, сколько изготавливает деталей рабочий за 1 час (Да, нужно его выработку разделить на время его работы)
— Ученик за 1 час? (Да, нужно его выработку разделить на время его работы)
— Зная производительность рабочего и ученика, можно ли ответить на вопрос задачи? (Да, для этого из большего числа вычтем меньшее)
Решение задачи самостоятельно
Самопроверка на мультимедиа
Составление выражения к задаче.
Сравните с выражением в учебнике. В чем разница?
Вывод: Чему мы учились, решая задачу? (ответы учащихся)
РАБОТА НАД ЗАДАНИЯМИ НА РАЗВИТИЕ ЛОГИКИ И СООБРАЗИТЕЛЬНОСТИ
— Для успешного усвоения нового материала мы использовали игру «Что? Где? Когда?», подведем итоги игры.